一类非自治地球物理方程的拉回指数吸引子

韩英豪, 傅 雪, 周雪莹, 李 铮

(辽宁师范大学 数学学院,辽宁 大连 116029)

海洋和大气的大尺度动力学方程是由Navier-Stokes方程导出的一个偏微分方程组,是热力学和盐度扩散输运方程耦合而成的.该方程组考虑了Boussinesq逼近下的浮力和分层效应.由于海洋和大气的低矮性,即流体层的深度与地球半径相比非常小,海洋的垂直方向流动比大气水平方向的流动小得多,因而通过流体静力平衡来模拟垂直运动可得到如下大尺度海洋和大气动力学的原始方程组[1-5]：

(1)

方程组的定义域为Ω=M×(-h,0),其中,M是以∂M为光滑边界的2中的一个有界区域,h为给定正常数.该方程组以三维速度场(v1,v2,w),v=(v1,v2),温度T和压强p作为未知函数.是3中的垂直单位矢量,f=f0+βy为Coriolis常数,R0是与地球自转对海洋动力行为的影响相关联的Rossby常数,Q(x,y,z,t)是给定的热源函数.在方程组中黏度算子L1和热扩散算子L2的定义分别为

和

1 准备工作

用Γu,Γb和Γl分别表示Ω的上边界、下边界和侧边界,即:

对方程组(1)施加如下边界条件:

(2)

并初始条件为

(3)

下面证明上述方程所产生的动力过程{U(t,τ)}t≥τ在函数空间(H2(Ω))3∩V中的拉回指数吸引子的存在性.其中,空间V的定义如下.令

(4)

定义在H1上的线性无界算子A1和在L2(Ω)上的线性无界算子A2:

(5)

那么,对任意v1,v2∈V1,T1,T2∈V2,w∈H1,有

对任意u,v∈((H2(Ω))2∩V1),w∈H1, 定义双线性算子B1(u,v):((H2(Ω))2∩V1)×((H2(Ω))2∩V1)→H1,使得

对任意χ∈((H2(Ω))2∩V1),φ∈(H2(Ω)∩V2),ζ∈L2(Ω),定义双线性算子

B2(w,φ):((H2(Ω))2∩V1)×(H2(Ω)∩V2)→L2(Ω),

使得,

那么方程组(1)～方程组(3)可以写成如下简约形式:

(6)

其边界条件为

(7)

初始条件为

(8)

因而,在V中可定义连续过程{U(t,τ):τ≤t}:

U(t,τ)(vτ,Tτ)=(v(t),T(t)):=(v(t;τ,(vτ,Tτ)),T(t;τ,(vτ,Tτ))).

对于∀t<τ,满足

(i)U(τ,τ)=IdV(V上的恒等映射)；

(ii)U(t,τ)=U(t,r)U(r,τ).

定理2[6]对任意T0∈,如果那么,对于t≤T0,非自治动力过程{U(t,τ):t≥τ}在V上拥有一个有界拉回吸收集其直径仅依赖于方程组的系数h,δ,α,Rt1,Rt2,Re1和Re2的大小.因而, 当时,非自治动力过程{U(t,τ):t≥τ}在V上拥有一致有界拉回吸收集其拉回吸收时间仅依赖于有界集合B的直径以及t-τ的大小.

2 拉回指数吸引子的存在性

(i){U(t,τ)}在X中存在一致有界吸收集

U(t,t-τ)B⊂B(t), ∀τ≥τ0.

(ii)存在0<δ<1,0<θ<1-δ,T1>0,有限维子空间X1⊂X,对于任意u,u1,u2∈D和t∈,有

‖U(t,τ)u1-U(t,τ)u2‖≤l‖u1-u2‖,l>0,∀t,τ∈[kT1,(k+1)T1], ∀k∈,

(9)

‖(I-Pm)(U(t,t-T1)u1-U(t,t-T1)u2)‖≤δ‖u1-u2‖,

(10)

(11)

其中，δ的值不依赖于t的值,Pm:X→X1是一个有界投影,m是X1的维数.

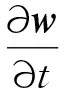
(12)

对方程(12)的两端与L1w做内积,得到

(13)

把式(13)整理,得到

(14)

(15)

利用Gronwall引理,从式(15)得到

‖w(t)‖2≤‖w(τ)‖2ec(t-τ).

令w=w1+w2,其中，w1是w在PH内的投影,将方程式(12)两侧与L1w2做内积,可得

(16)

利用Young不等式,将等式(16)整理得到

通过使用Poincaré不等式:λn‖w2‖2≤‖L1w2‖2,从上式得到

(17)

利用Gronwall引理,从式(17)得到

进一步整理上式,得到

当λn的值充分大时,即可得式(10).

令Hm=span((w1,η1),(w2,η2),…,(wm,ηm)),Pm:H→Hm是L2(Ω)在Hm上的正交投影.设

(v(t),T(t))=U(t,τ-s)(vτ,Tτ)=(v1+v2,T1+T2),

其中，有(v1,T1)=Pm(v,T),(v2,T2)=(I-Pm)(v,T).

将方程组(1)中的第一个等式两端与L1v2做内积,得到

利用Young不等式,从上式得到

进而得到

(18)

其中,

因此,当m充分大时,从式(18)中得到

同理,对任意ε>0,t∈,τ≤τ2-1,当m充分大时,有总之,对任意ε>0,t∈,τ≤τ2-2,当m充分大时,有‖v2(t)‖2+‖T2(t)‖2≤ε.综上所述,对任意ε>0,t∈,τ≤τ2-2,当m充分大时,即有

这就证明了式(11).证毕.