地铁车辆车体关键连接结构振动特性研究*

宋 浩，孟建军,2,3，董世昌

（1 兰州交通大学 机电技术研究所，兰州 730070；2 甘肃省物流及运输装备信息化工程技术研究中心；兰州 730070；3 甘肃省物流及运输装备行业技术中心，兰州 730070；4 兰州交通大学 机电工程学院，兰州 730070）

地铁车辆运行速度不断提高，并且地铁车辆车体向轻量化方向发展，这使得地铁车辆在较高速度运行时，车体轻量化引起的车体刚度不足导致车体产生剧烈振动。另外地铁车辆频繁的制动与启动加速了钢轨磨耗，轨道不平顺问题突出，使得地铁车辆在运行中容易产生剧烈振动。车体振动容易导致车体上的紧固件松动及结构疲劳损坏，因此需要对紧固件等关键连接结构进行服役安全性的研究。其中，关键是需要研究紧固件等关键连接结构在地铁车辆运行过程中受到的振动特性。为此，需要考虑车体柔性效应，并且建立车辆刚柔耦合动力学模型进行研究。近年来铁道车辆刚柔耦合动力学研究取得了显著的进展，Shi等［1］针对京沪线动车组出现的车体柔性振动共振现象进行研究，结果表明高频激励源于转向架的蛇行运动接近车体的模态，通过对轮轨进行重新打磨，蛇行运动减弱，从而避免了共振现象。Chen等［2］采用有限元分析方法和多体系统动力学理论研究了柔性车体对车辆系统动力学性能的影响，建立了车辆刚柔耦合系统动力学模型，通过振动传递函数分析了车身关键部位的振动，发现车体结构振动对车辆系统动力学性能的影响在车体固有振动频率方面尤为明显。Jun［3］等应用断裂力学计算破裂的动车组底架的临界裂纹尺寸和裂纹扩展速率，通过比较有限元分析和物理载荷测试获得的侧边梁的变形来对有限元模型进行验证。Seo等［4］为了评价城市轨道交通车辆铝合金车体的疲劳强度，提出了一种模拟实际动载荷的大型试验方法，并对铝合金车体的疲劳失效进行了研究。Yoon等［5］对地铁车辆车体及其关键连接结构进行了有限元分析及加载试验，验证了最大载荷下车体结构的安全性和功能性。程海涛［6］和邬平波［7］应用柔性多体系统动力学进行货车动力学仿真研究，分析了车体的弹性效应对车辆运行稳定性的影响。朱浩等［8］基于车辆刚柔耦合系统动力学模型，设计了一个模糊控制器来抑制柔性车体的动态响应，实现了基于柔性车体的车辆主动悬挂的隔振。周劲松等［9］建立了包含结构阻尼的铁道车辆垂向刚柔耦合动力学模型，研究了铁道客车车体弹性对运行平稳性的影响。刘国云等［10］研究了钢轨波磨对高速车辆系统振动特性的影响。刘佳等［11］针对某高速列车轴箱连接螺栓松动现象，对踏面磨耗状态及列车关键部件振动特性进行测试，分析了轴箱频率振动与车轮非圆化磨耗之间的相关性，初步探究了轴箱端盖螺栓易松动的原因。石怀龙［12］和吴会超［13］等通过建立高速动车组的车辆刚柔耦合动力学模型，研究了车体和车下设备之间的耦合振动关系及不同参数相互作用下的振动特性。Zhu等［14］阐述了地铁车辆车体碰撞过程中关键部件的变形、能量吸收和冲击力之间的内在联系。李凡松［15］和孙善超［16］等针对动车组车体异常振动进行了探究。Takigami［17］研究了通过压电材料来降低弹性振动。

为了分析地铁车辆车体关键连接结构振动特性，文中以刚柔耦合动力学理论为基础，对车体进行有限元分析，并且基于柔性车体建立了车辆刚柔耦合动力学模型。仿真分析了车体关键连接结构振动特性，并且对该型地铁车辆车体关键连接结构振动进行了现场试验。通过建模仿真分析与实际试验结果对比，初步获取了地铁车辆车体关键连接结构振动特性，并研究了地铁车辆车体关键连接结构的频谱能量来源及造成地铁车辆车体关键连接结构疲劳损坏或连接处螺栓松动的原因，为改善关键连接结构疲劳及螺栓松动提出合理的解决方案。

1 车体振动试验及结果分析

1.1 车体振动测试

为了获取地铁车辆车体关键连接结构振动特性，在中车某车辆厂的静调线上进行了地铁车辆车体关键连接结构振动试验，如图1所示。

图1 地铁车辆车体关键连接结构振动试验

在试验过程中，为了获取关键连接结构振动，在相应位置处分别布置加速度传感器。关键连接结构以司机室底铆螺母安装处和左侧车顶吊挂梁安装螺栓处为例说明，如图2所示。司机室底铆螺母安装处位于司机室底部的车体底架下端，用于连接司机室与车体底架，此处连接结构刚度较低，容易产生较大振动；左侧车顶吊挂梁安装螺栓用于吊挂梁与车体的连接，而车顶吊挂梁用于承载空调机组及受电弓，因而左侧车顶吊挂梁安装螺栓承受载荷较大，在受到振动时，容易产生松动。

图2 地铁车辆车体关键连接结构

测试工况：启动、加速、匀速、减速，从而模拟地铁车辆实际运行工况。

由于所采集信号为全工况时域数据，可以进行能量值比较，从而确定螺栓所受最大振动方向。具体则以加速度均方根值（Root Mean Square，RMS）作为时域能量参数。3次测试数据各方向能量值见表1。

由表1可得，列车全工况运行时，司机室底铆螺母安装处以横向为实际激励的主要方向，振动能量贡献最大。左侧车顶吊挂梁安装螺栓处则以垂向为实际激励的主要方向，振动能量贡献最大。司机室底铆螺母安装处横向振动加速度响应测试结果如图3（a）所示，峰值为0.25g左右；左侧车顶吊挂梁安装螺栓处垂向加速度响应测试结果如图3（b）所示，峰值为0.2g左右。

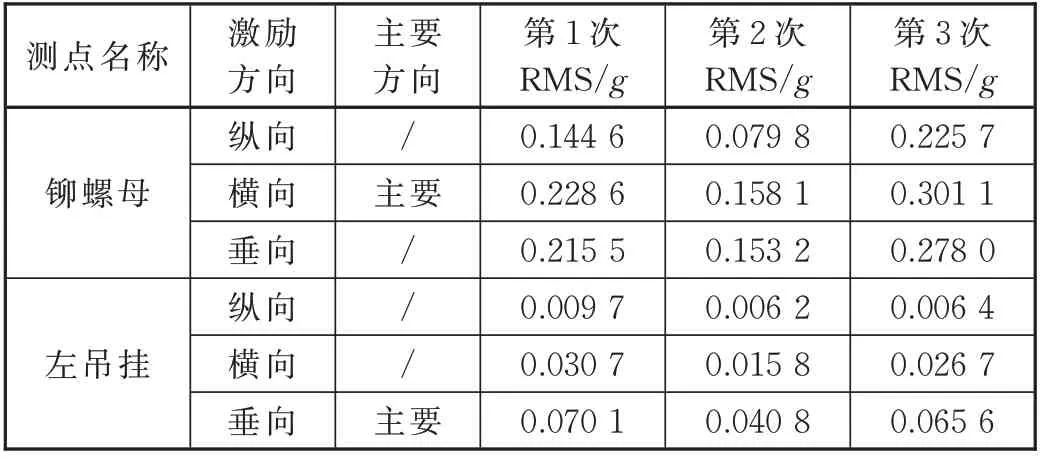
表1 3次测试数据各方向能量值比较

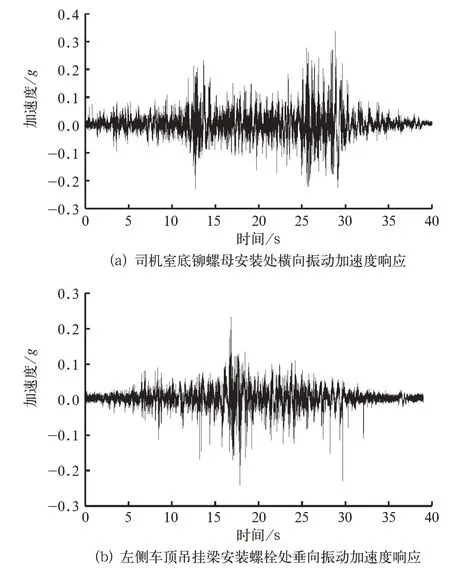
图3 车体关键连接结构加速度响应

1.2 振动特性的频域分析

由于整个测试条件为全工况行驶，信号具有非平稳特征，适合的频域分析方法为提取振动的功率谱密度（Power Spectral Density，PSD），可以获得对测点贡献主要能量的频率。车体关键连接结构振动加速度功率谱密度如图4所示。

图4 车体关键连接结构振动加速度功率谱密度

2 柔性车体建模

首先定义点p为绝对坐标系中柔性车体上的任一点的坐标，可表示为式（1）：

式中：Px、Py、Pz为局部坐标系在整体坐标系里的3个坐标分量；α、β、γ为局部坐标系在绝对坐标系中的欧拉角；τi为模态振型，i为所选取的模态阶数；P、H为各坐标系中的矢量集；τ为模态振型的向量集。

如果将车体划分为j个单元，则动能可表示为式（2）：

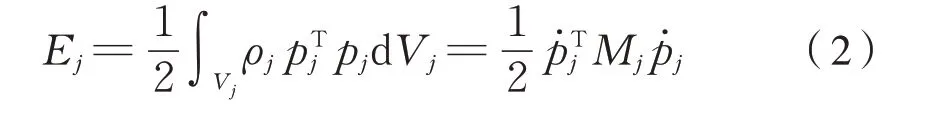
式中：ρj和V j分别为单元体j的密度和体积；M j为柔性车体单元质量矩阵。

车体的动力学方程可用拉格朗日方程表示为式（3）：

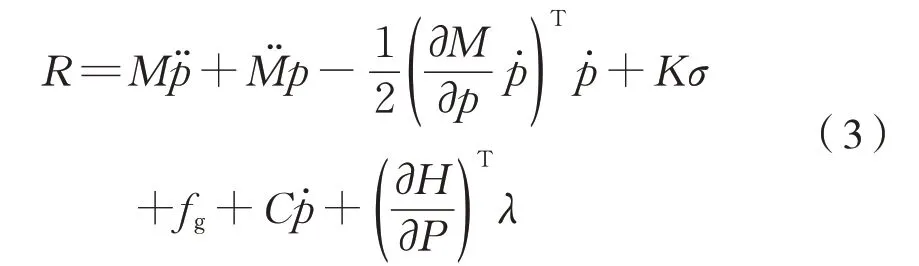
将式（3）写为式（4）：

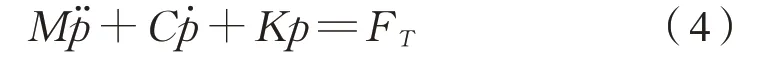
式中：M、C和K分别为柔性车体的质量矩阵、阻尼矩阵和刚度矩阵；fg为重力；λ为约束方程T的拉格朗日乘子；R为广义力矩阵；FT为外力矩阵。

3 车体有限元模型构建及模态分析

以某型地铁车辆头车车体作为研究对象，采取必要的简化，建立车体的三维模型，并导入到HyperMesh软件中进行柔性化处理，建立有限元模型，并进行模态分析。模态频率与振型取前12阶，见表2。

表2 前12阶模态频率和振型

由于前6阶模态为刚体模态，因此振型图取7～12阶模态，如图5所示。

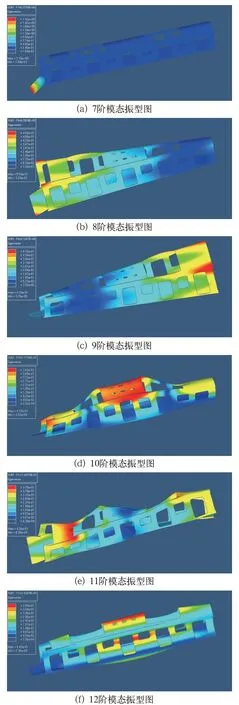
图5 车体7~12阶模态振型图

4 车辆刚柔耦合动力学建模与仿真分析

4.1 车辆刚柔耦合动力学建模

将车体的模态分析结果导出为*.MNF（模态中性文件），并导入ADAMS/Rail软件中，如图6所示。

图6 柔性车体模型

在车体的关键连接结构的节点处建立测量点。关键连接结构以司机室底铆螺母安装处和左侧车顶吊挂梁安装螺栓处为例说明，如图7所示。

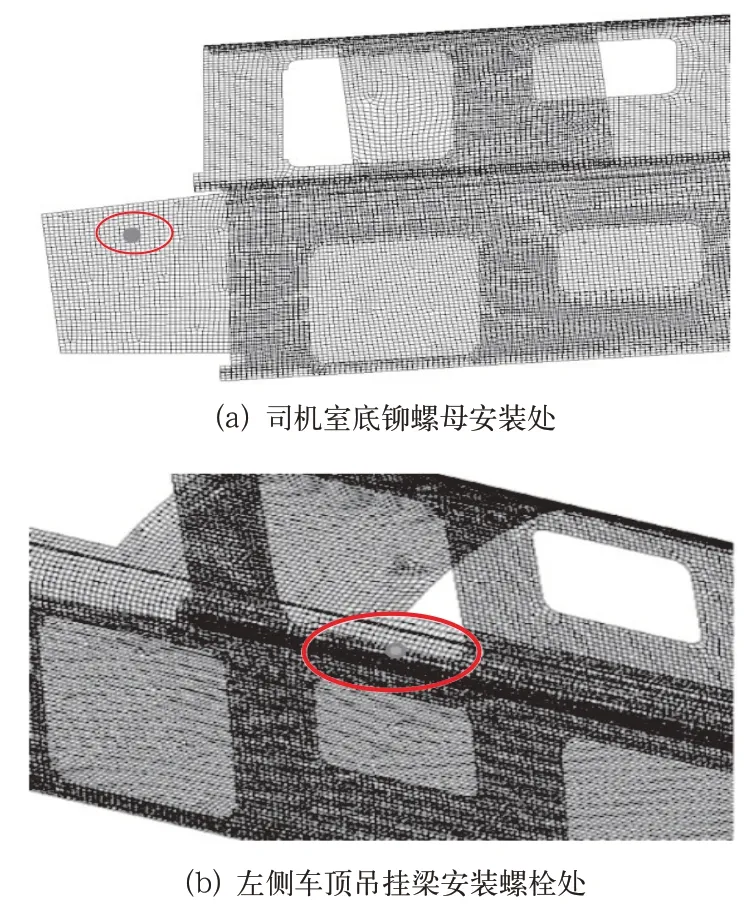
图7 地铁车辆车体关键连接结构

最后将柔性车体与转向架装配，建立车辆刚柔耦合动力学模型。如图8所示。

图8 车辆刚柔耦合动力学模型

4.2 仿真结果及分析

对地铁车辆刚柔耦合动力学模型进行动力学仿真计算，首先在ADAMS/Rail软件中进行仿真设置，轨道属性采用直线轨道的德国高干扰谱。为了保证在仿真时间内，线路长度满足车辆运行需要，线路长5 000 m，其中轨道无激励长度为20 m，不平顺长度为4 980 m，这样设置保证列车运行之初，积分运算能顺利进行。

车辆运行速度从0开始加速，加速度为0.98 m/s2，在速度达到80 km/h后以制动减速度为1.2 m/s2开始减速，直到速度为0。模拟地铁车辆在站点之间的加减速运行情况，仿真时间约为40 s。

根据表1得到的关键连接结构激励主要方向，对车体司机室底铆螺母安装处横向加速度响应和左侧车顶吊挂梁安装螺栓处垂向加速度响应进行仿真计算，结果如图9所示。

图3 的实测结果与图9的仿真结果相当，振动变化趋势基本一致，司机室底铆螺母安装处横向加速度峰值在0.25g左右，左侧车顶吊挂梁安装螺栓处垂向加速度响应峰值在0.2g左右。

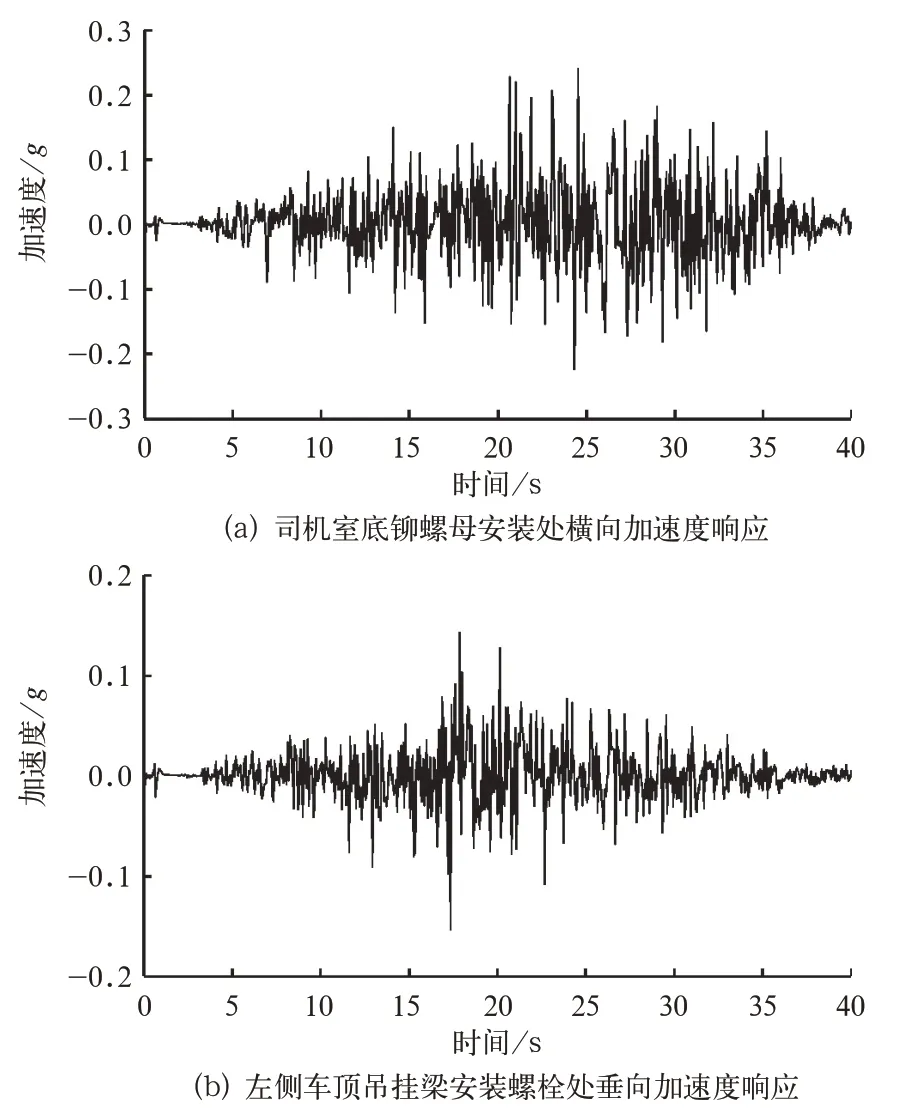
图9 车体关键连接结构加速度响应

车体司机室底铆螺母安装处横向振动功率谱密度和左侧车顶吊挂梁安装螺栓处垂向振动功率谱密度如图10所示。

图4的实测结果与图10的仿真结果相当，司机室底铆螺母安装处横向振动的主要频率在8 Hz左右，与车体第7阶模态振型司机室底架变形对应的频率一致。从图5（a）中可得，第7阶模态中，发生较大弯曲变形的结构位于司机室底架处即司机室底铆螺母安装处，与测点位置吻合。左侧车顶吊挂梁安装螺栓处垂向振动的主要频率在14 Hz左右，与车体第11阶柔性模态振型一阶扭转对应的频率基本一致。从图5（e）中可得，在第11阶模态中，左侧车顶吊挂梁处发生较大扭曲变形，与测点位置吻合。

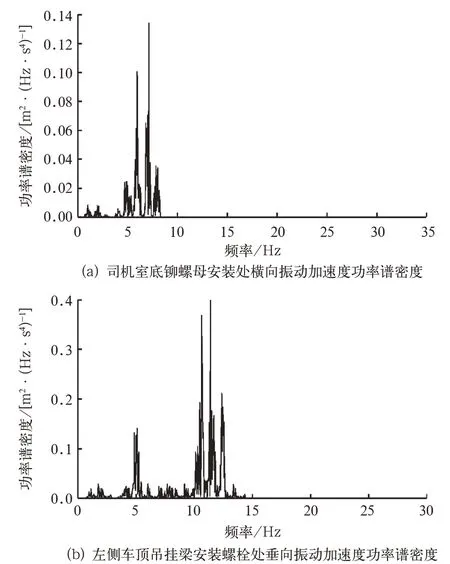
图10 车体关键连接结构振动加速度响应功率谱密度

由此表明，地铁车辆运行中的外部激励由一系和二系悬挂衰减传递到车体上后主要为低频振动量。因此，地铁车辆车体关键连接结构的频谱能量来源主要是低频振动，又因为低频振动频率接近车体模态频率，容易引起车体共振，使得连接螺栓松动或关键连接结构疲劳损坏。因此，可以得到判断，造成这2处紧固件松动或结构疲劳损坏的主要振动量在50 Hz以下，且主要频率大约为8 Hz和14 Hz。

试验结果与仿真结果契合也验证了动力学模型的准确性，因此对动力学模型进行进一步分析，研究在其他工况下的车体关键连接结构振动特性。依据地铁车辆实际运行情况，选取地铁车辆高速匀速运行工况与轨道不平顺较差的工况进行仿真计算。仿真结果由图11～图14所示。图11为在90 km/h与70 km/h的匀速下，地铁车辆车体司机室底铆螺母安装处横向加速度对比，图12为在90 km/h与70 km/h的匀速下，地铁车辆车体司机室底铆螺母安装处横向加速度功率谱密度对比。图13为轨道不平顺情况良好与较差情况下，地铁车辆车体司机室底铆螺母安装处横向加速度对比，图14为轨道不平顺情况良好与较差情况下，地铁车辆车体司机室底铆螺母安装处横向加速度功率谱密度对比。

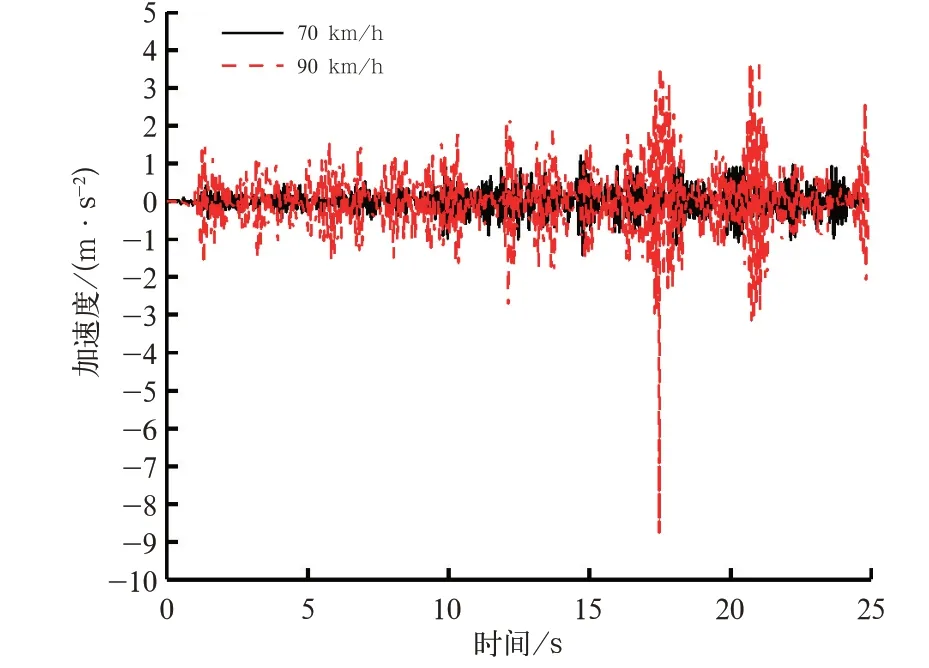
图11 不同速度下司机室底铆螺母安装处横向加速度对比

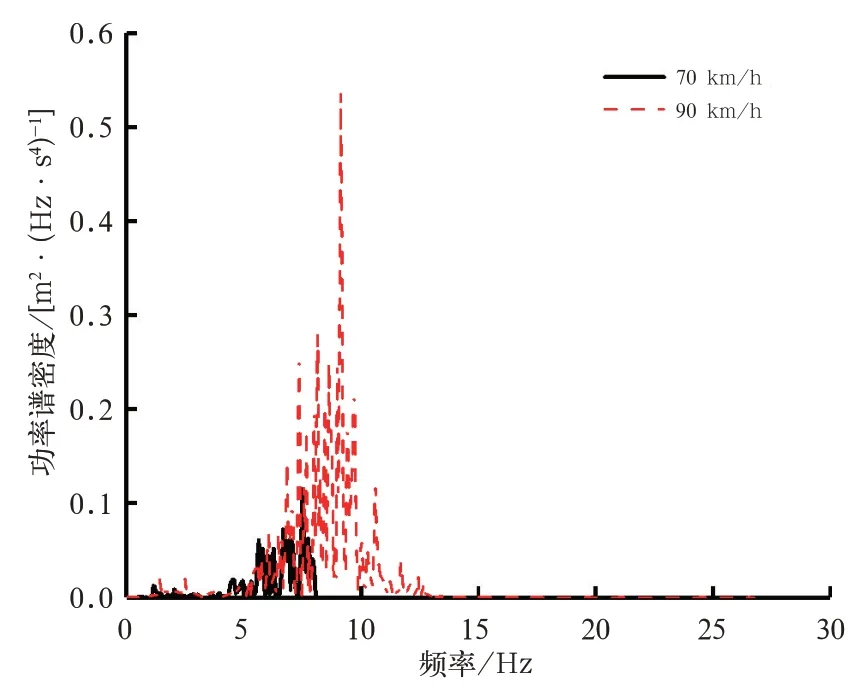
图12 不同速度下司机室底铆螺母安装处横向加速度功率谱密度对比

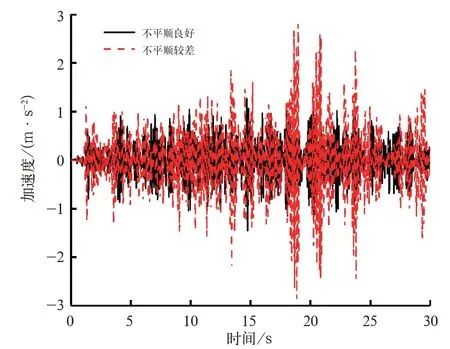
图13 不同轨道工况下司机室底铆螺母安装处横向加速度对比

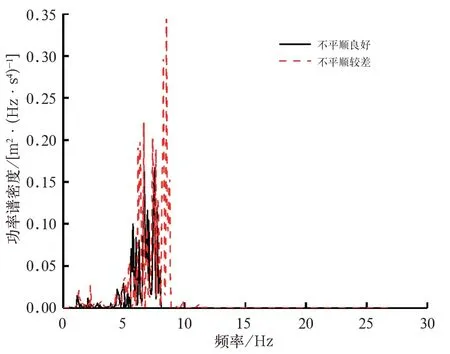
图14 不同轨道工况下司机室底铆螺母安装处横向加速度功率谱密度对比

由图11可得，地铁车辆在90 km/h的速度下运行，振动加速度要明显高于运行在70 km/h的速度下的振动加速度，而从图12可得，虽然在2种速度工况下，司机室底铆螺母安装处横向振动的主要能量输入频率都在8 Hz左右，但是随着速度提升，频率逐步增加，并且功率谱密度值大幅上升。这表明：随着地铁车辆运行速度提高，主要能量输入频率提升，容易激发车体高阶柔性模态，导致车体剧烈振动。

由图13可得，在轨道不平顺较差的情况下，地铁车辆运行的振动加速度要明显高于轨道不平顺良好的情况，而从图14可得，虽然2种轨道不平顺工况下，司机室底铆螺母安装处横向振动的主要能量输入频率都在8 Hz左右，但是随着轨道不平顺情况恶化，主要振动频率有所增加，并且功率谱密度值上升75%。这表明：随着轨道不平顺情况恶化，外部激励加剧，主要能量输入频率提升，容易激发车体高阶柔性模态，导致车体剧烈振动。

5 结论

为了研究地铁车辆车体关键连接结构振动特性，通过搭建地铁车辆刚柔耦合动力学模型，着重对关键连接结构节点进行仿真计算，并进行了现场测试，获取了地铁车辆车体关键连接结构的振动，并且对振动进行频谱分析，得到了相应的振动特性，仿真计算结果与实测结果进行比较，二者结果吻合良好，验证了模型的合理性，并且得出以下结论：

（1）地铁车辆运行中的外部激励经过一系和二系悬挂衰减之后，传递到车体上主要为低频振动量，且主要振动量在50 Hz以下，造成2处关键连接结构疲劳损坏或连接螺栓松动的主要振动频率大约为8 Hz和14 Hz。

（2）车体关键连接结构处的振动频率接近车体柔性模态频率，容易激发车体柔性模态共振，造成车体剧烈振动，从而导致关键连接结构疲劳损坏或连接处螺栓松动。

（3）地铁车辆运行速度不断提高及轨道不平顺情况恶化，会导致外部激励加剧，主要振动频率会有所增加，容易激发车体高阶柔性模态，导致车体剧烈振动。

（4）研究结果为关键连接结构处的紧固件以及疲劳损坏等服役安全性研究提供理论基础。在疲劳可靠性试验和紧固件预紧力动态衰减特性试验时，可以考虑以低频作为主要激励频率。对于新设计的地铁车辆可以考虑提升车体一阶模态频率降低车体的弹性振动或者通过车体上加装作动器或阻尼层等来抑制车体的弹性振动。