Thermophysical properties of pure gases and mixtures at temperatures of 300–30 000K and atmospheric pressure:thermodynamic properties and solution of equilibrium compositions
Zhongyuan CHI (池中源) , Weijun ZHANG (张卫军) and Qiangda YANG (杨强大)
School of Metallurgy, Northeastern University, Shenyang 110819, People’s Republic of China
Abstract The equilibrium compositions and thermodynamic properties (density, enthalpy, etc at constant pressure)of plasma of pure gases and mixtures under local thermodynamic nonequilibrium have been calculated in this paper.The homotopy Levenberg–Marquardt algorithm was proposed to accurately solve nonlinear equations with singular Jacobian matrices, and is constructed by the Saha equation and Guldberg–Waage equation combined with mass conservation, the electric neutrality principle and Dalton’s partial pressure law,to solve the problem of dependence on the initial value in the process of iteration calculation.In this research, the equations at a higher temperature were solved and used as the auxiliary equations, and the homotopy control parameters’ sequence of the homotopy equations was selected by equal ratios.For auxiliary equations, the iterative initial value was obtained by assuming that there were only the highestvalence atomic cations and electrons at this temperature,and the plasma equilibrium composition distribution with the required accuracy was ultimately solved under the current conditions employing the Levenberg–Marquardt algorithm.The control parameter sequence was arranged according to the geometric sequence and the homotopy step was gradually shortened to ensure continuity of the homotopy process.Finally, the equilibrium composition and thermodynamic properties of pure N2,Mg(30%)–CO2(70%)and Mg(40%)–CO(50%)–N2(10%)mixture plasma at atmospheric pressure were calculated and the calculation process of some specified temperatures was shown and analyzed.The calculation accuracy of equilibrium composition is higher than other findings in the literature.The results for the thermodynamic properties are in good agreement with data reported by the literature.
Keywords:plasma equilibrium compositions,thermodynamic properties,homotopy Levenberg–Marquardt algorithm (HLMA), auxiliary equations
1.Introduction
Plasma, as a new clean and important energy source, has the advantages of high temperature, high enthalpy, high energy concentration, and controllable compositions.Hence, it has been widely used in metallurgy [1], electric-arc furnaces [2],semiconductor processing [3], material surface modification[4],environmental protection[5],and other fields.Plasma is a mixture of neutral molecules and/or atoms produced by a series of chemical reactions.It is composed of electrons,neutral molecules, atoms, and their cations with high conductivity, heat conduction, and fluidity.The thermodynamic properties are the necessary characteristic parameters for analyzing the temperature distribution in a plasma region.For further studies on plasma application, the exact composition distribution in thermal plasma is the basic condition for calculating or obtaining thermodynamic properties.However, it is very difficult to directly solve a nonlinear problem such as the plasma equilibrium composition model iteratively,and the difficulty lies in the determination of the initial iteration values.In this paper, a new homotopy Levenberg–Marquardt algorithm (HLMA) is proposed to solve the nonlinear problem based on the particularity of higher temperature and the composition distribution of some plasma is calculated;the corresponding thermodynamic parameters are obtained at the same time.
For the calculation of plasma thermomechanical parameters, the handing method is simple and easy if the particle number density and internal partition function are given[6, 7], which will not be described in too much detail here.The models expressing the plasma composition have two forms.The first one is composed of the mass conservation equation,Dalton’s law, and the charge conservation equation combined with the Saha equation and the Guldberg–Waage equation.The other one is obtained by solving the minimum Gibbs free energy of the plasma system.These two forms are equivalent in gas[8,9].The first method directly presents the physical and chemical process of plasma formation, the Saha and Guldberg–Waage equations are in the form of the equations, and abstract mathematical model is intuitive and simple.
For modeling the plasma composition, some researchers have done a lot of studies.Cressault [10] calculated the plasma composition and the net emission coefficient (NEC)for Ar–H2–He thermal plasma in local thermodynamic equilibrium at atmospheric pressure.Murphy and Arundelli [11]determined the equilibrium composition of thermal plasma using the principle of minimization of the Gibbs free energy.Wang [12] determined the equilibrium composition and thermodynamic properties of carbon and water in the temperature range of 400–30 000 K and the pressure range of 0.1–10 atm by the method of Gibbs free energy minimization.Gleizes and Chervy[13]calculated the composition of a twotemperature SF6plasma in the pressure range of 0.1–1.6 MPa using the generalized Saha and Guldberg–Waage equations.Colombo and Ghedini[14]obtained the chemical equilibrium composition and determined the thermodynamic and transport properties in nonequilibrium argon, oxygen, and nitrogen thermal plasmas.Gordana [15] calculated the equilibrium plasma composition of a U-shaped argon-stabilized DC arc based on minimization of the Gibbs free energy.
In both forms, they eventually converge to a system of nonlinear equations; Gordon and Mcbride [16] minimization is the most popular method to solve the plasma composition model, and Lagrange multipliers along with steepest descent Newton–Raphson iteration are utilized to solve the nonlinear equation system numerically [12–14].Godinet al[17] proposed a methodology that uses the chemical basis concept to reduce to a minimum the order of the system of equations to solve.Frolov and Ivanov [18] solved these equations by the modified Newton method for increments of logarithms of unknown values.Maria[19]and Zhonget al[20]constructed a new distribution function according to the maximum entropy principle and the statistical theory methods for gases with physical and chemical processes, to avoid solving the Saha equations.However, these methods have an obvious disadvantage in that they are sensitive to the iteration initialization and the globally optimal solution cannot be obtained if no reasonable initial values are given.
In order to find the global optimal solution,the HLMA is proposed, and this method combines the advantages of the Levenberg–Marquardt algorithm (LMA) and homotopy analysis method(HAM).The LMA is an iterative method located between the Gauss–Newton method and the steepest descent method, and can be used to deal with singular nonlinear equations [21]; meanwhile, the adaptive step size also improves the chance of escaping local optimality during iteration.The HAM is a global convergence algorithm and is not constrained by the initial values[22].These methods play important roles in solving nonlinear equations.Fan [23]introduced the linear search for the approximate Levenberg–Marquardt (L-M) step, improved the convergence speed, and reduced the calculation load.Chen [24] established a highorder accelerating modified L-M method by adjusting the approximate L-M step one more time at every iteration.The convergence order of this new method was shown to be fourth.However, the LMA has the problem that the initial values are difficult to determine like other iterative methods.The HAM has been developed for the solution of nonlinear ordinary differential equations with a fractional order [25].Abbasbandy [26] applied the HAM to solve the nonlinear heat transfer problem by adjusting and controlling the convergence region.However,the HAM has insufficient ability to deal with singular nonlinear equations.When the value oftkapproaches 1, the homotopy equations are singular, and how to adjust solutions to ensure the continuity of the iterative process is the key issue.
In this paper, the HLMA is proposed to solve singular nonlinear equations of modeling the plasma compositions.In this new algorithm, the advantage of the HAM with no constraint for the initial value is combined with the advantage of rapid convergence of the LMA realizing the solution of singular nonlinear equations.In other words, the HAM provides an exact iteration initial value for the LMA, and the LMA quickly solves the homotopy equations.For the HLMA,two important tasks must be taken into account, i.e., the auxiliary equations and the homotopy control parameters’sequences [tk].The equations expressing the plasma composition at a higher temperature which could be solved accurately were chosen as the auxiliary equations,and the control parameter sequences [tk] were constructed using the equilateral ratios.To demonstrate the accurate calculation of the plasma compositions by the HLMA, three example cases are described and discussed in detail in the third part.
Four parts are covered in this paper.Firstly, the mechanism of the plasma composition model under local thermodynamic nonequilibrium and thermal nonequilibrium parameter θ=Te/This elaborated based on the conservation equation of mass, the conservation equation of charge, Dalton’s law, and the Shah and Guldberg–Waage equations.Based on the theory of statistical thermodynamics, the calculation model of thermodynamic parameters is established.Secondly, the solution procedure of the plasma composition model is deduced by the HLMA to solve the auxiliary equations and set up the control parameter sequences [tk].Thirdly, in order to verify the general applicability of the algorithm, examples of different atomic species and different auxiliary temperatures are given to solve the problem,and the example calculations are shown to demonstrate the feasibility and accuracy of the HLMA method.Finally, the equilibrium compositions of pure N2, Mg–CO–N2and Mg-CO2mixture plasmas in specific proportions are calculated, and then the corresponding thermodynamic parameters are obtained.
2.Model of equilibrium compositions and thermodynamic properties
2.1.Equilibrium compositions
Plasma is a mixture of neutral molecules formed after a series of chemical reactions.The total pressure of the mixture is the sum of the gas pressure of each component,
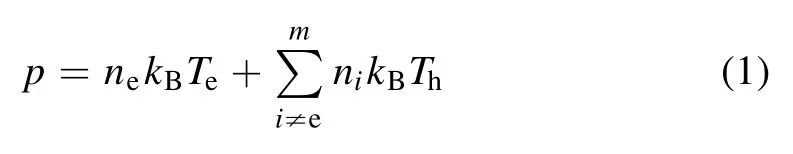
wherepis the total pressure of the plasma;neandniare the number densities of electrons and theith particle, respectively;kBis the Boltzmann constant; andTeandThare the electron and heavy temperatures of the plasma, respectively.θ=Te/This the thermal nonequilibrium parameter.
The ratio of the number densities of two different elements is constant:

wherenziis the number density of theith atom element andnz1is the number density of the first atom element.
The plasma is neutral on the macro level:

whereziis the electric charge of theith particle including electrons.
The ionization reactionar→a(r+1)++e and dissociation reactionab→a+bare the main chemical reactions in plasma.The chemical equation and the chemical equilibrium relationship among the concentrations of different molecules can be expressed by the Saha equation equation (4) and Guldberg–Waage equation (5),
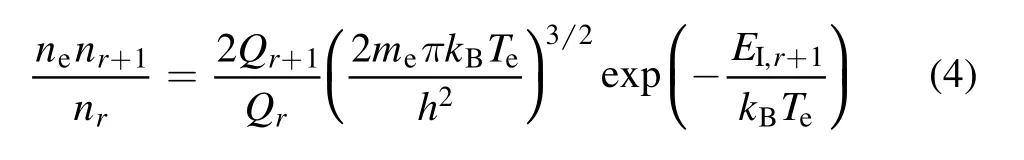

where e is an electron,meis the mass of an electron,andhis the Planck constant.AB represents a polyatomic molecule, and A and B are the products of the decomposition AB.nAB,nA,nB,mAB,mA, andmBare the number density and mass of AB, A,and B, respectively.QrandQr+1are the partition functions of the atoms and their ions,respectively,QAB,QA,andQBare the partition functions of the AB,A,and B molecules,respectively,andEI,r+1andEdare the ionization and dissociation energies of the associated chemical reaction,respectively.The calculation of the partition coefficient can be referred to in the relevant literature [14, 27, 28], but will not be introduced here.
The model can be expressed by equations (1)–(5).They include one charge conservation equation, one pressure balance equation,Ne−1 mass conservation equations(Neis the number of atomic types and these equations do not exist ifNe=1), andm−Ne−1 chemical equations.
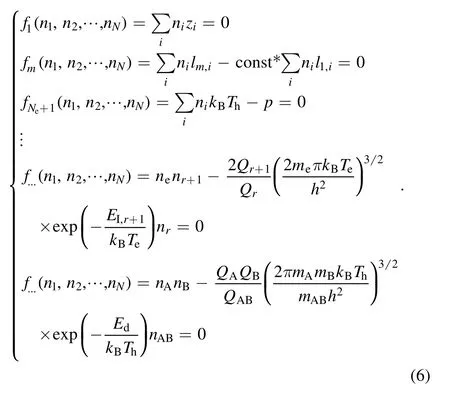
The values of the right-hand side of equations (4) or (5)are significantly different between the different chemical reactions.For example, in the air plasma, whenT=3000 K,their maximum value divided by their minimum value may equal nearly 108which is the main reason for the singularity of the equation system.Moreover, the coefficients of other equations are less than or around 10 while the coefficients of the chemical reactions are in the range of 10−5–1010.The Saha and Guldberg–Waage equations can be expressed by equation (7) in terms of vectors so that equation (6) can be expressed as equation (8):
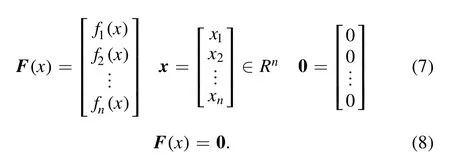
2.2.Partition function
The atom partition function is the sum of electron level states,diatomic molecules are the result of interactions between electronic, vibrational, and rotational energy levels, and a polyatomic molecule is the product of simple harmonic partition functions ignoring the contribution of rotational energy levels.
For atoms and their ions,
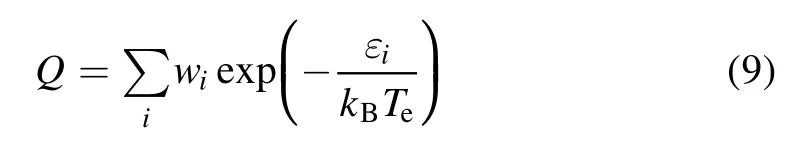
wherewiand εiare the degeneracy (statistical weight)and energy level of theith energy level of the atom, respectively.Atomic energy levels are based on the latest spectral data from the National Institute of Standards and Technology(NIST) [29].
For diatomic molecules and their ions,
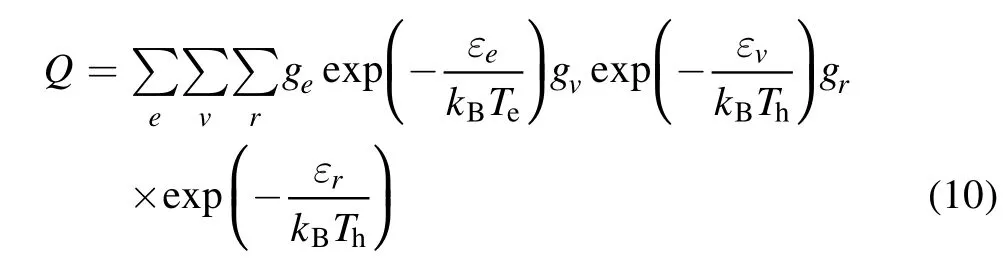
where εe,εv,εr,ge,gv,andgrare the electron vibrational,rotational energy level, and the corresponding degeneracy of the molecule, respectively.
The vibration energy of thevth vibrational state andeth electronic state can be computed as
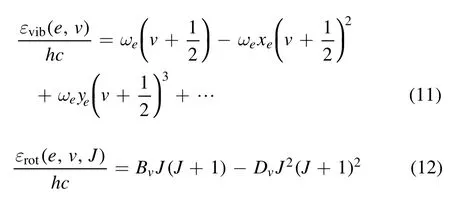
where ωe, ωexe, ωeye,Be,De, αe, and βeare the spectroscopic constants of theeth electronic state of a diatomic molecule.BecauseDvis much smaller thanBv,theDvterm is ignored when calculating the rotational energy levels in order to simplify the calculation.
For polyatomic molecules,
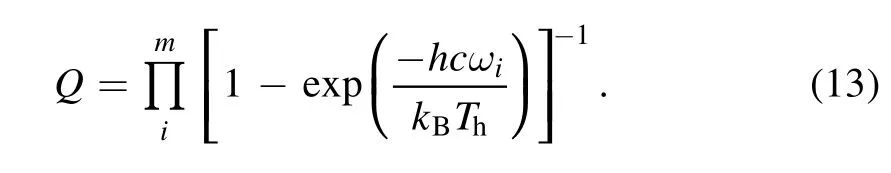
For linear molecules, vibrational degrees of freedomm=3n−5, nonlinear moleculem=3n−6, andnis the number of atoms in the molecule.
2.3.Thermodynamic properties
Once compositions and partition functions are known, it is possible to compute the thermodynamic properties.According to statistical thermodynamics, and given the number densities, the average density equation (14), internal energy equation (15), specific enthalpy equation (16), and constantpressure specific heat equation (17) have been listed.

where ρ,e,h,andcpare the density,internal energy,enthalpy,and constant-pressure specific heat of plasma, respective.n,m, andEare the number density, mass, and formation enthalpy of a molecule, respectively, andQintrepresents the partition functions.It can be seen from equations (14)–(17)that the thermodynamic parameters are the summation of the data of different particles and can be calculated directly.
3.Homotopy Levenberg–Marquardt algorithm to solve plasma equilibrium compositions
3.1.HLMA
The HAM is based on both the homotopy in the topology and the Maclaurin series, and is a simple analytical technique for linear and nonlinear problems[24,25].This method does not require small or large parameters in the perturbation techniques, but it cannot be applied to singular nonlinear equation systems including the current equation system.In this paper,the LMA was combined with the HAM to solve singular nonlinear equations expressing the plasma composition model.The LMA was responsible for solving the homotopy equations, while the HAM was used to construct the homotopy equations and provide the iterative initial values for the LMA.The homotopy equations are expressed as
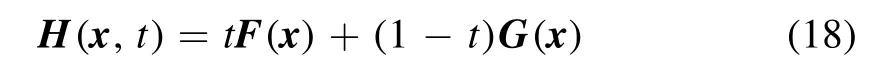
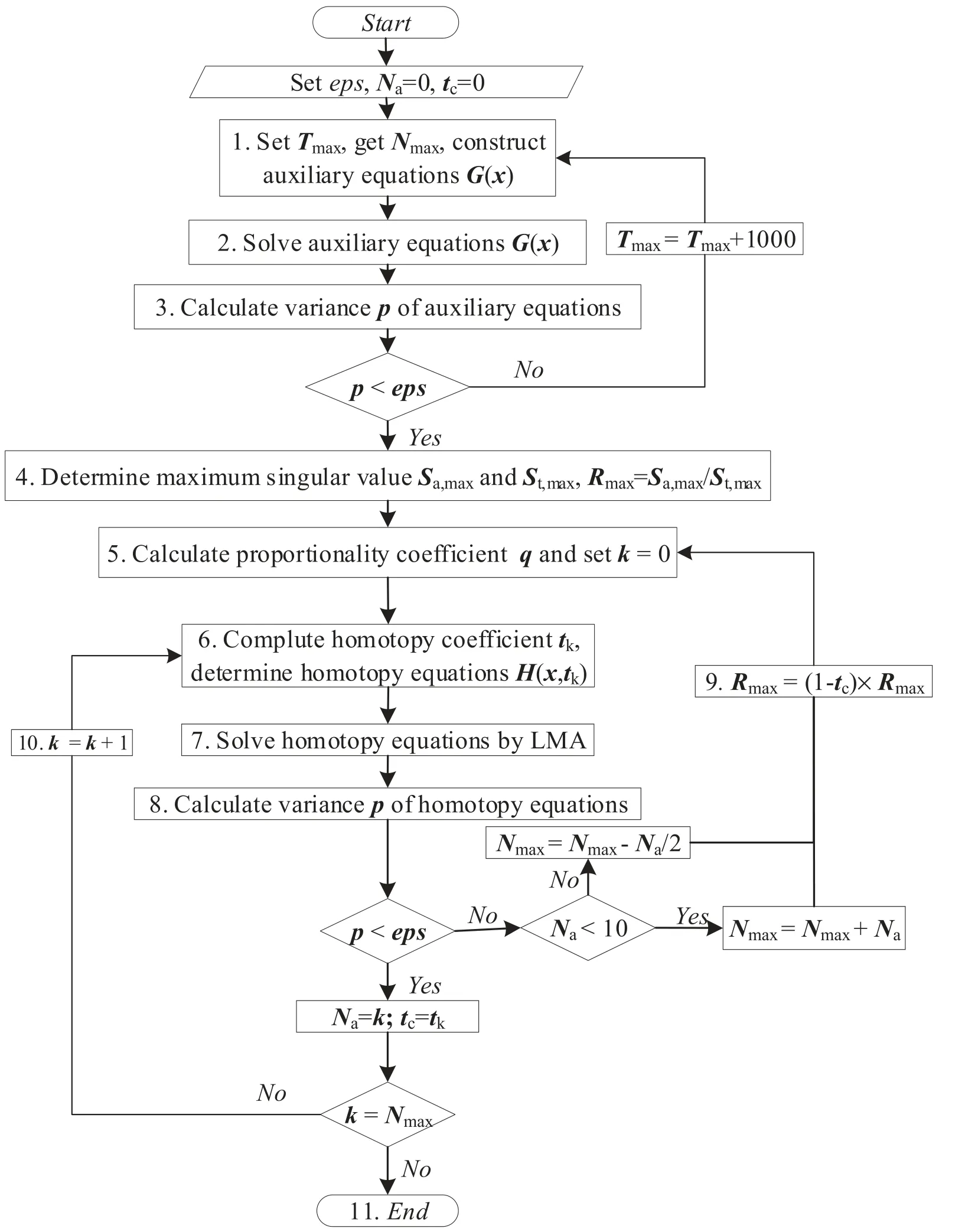
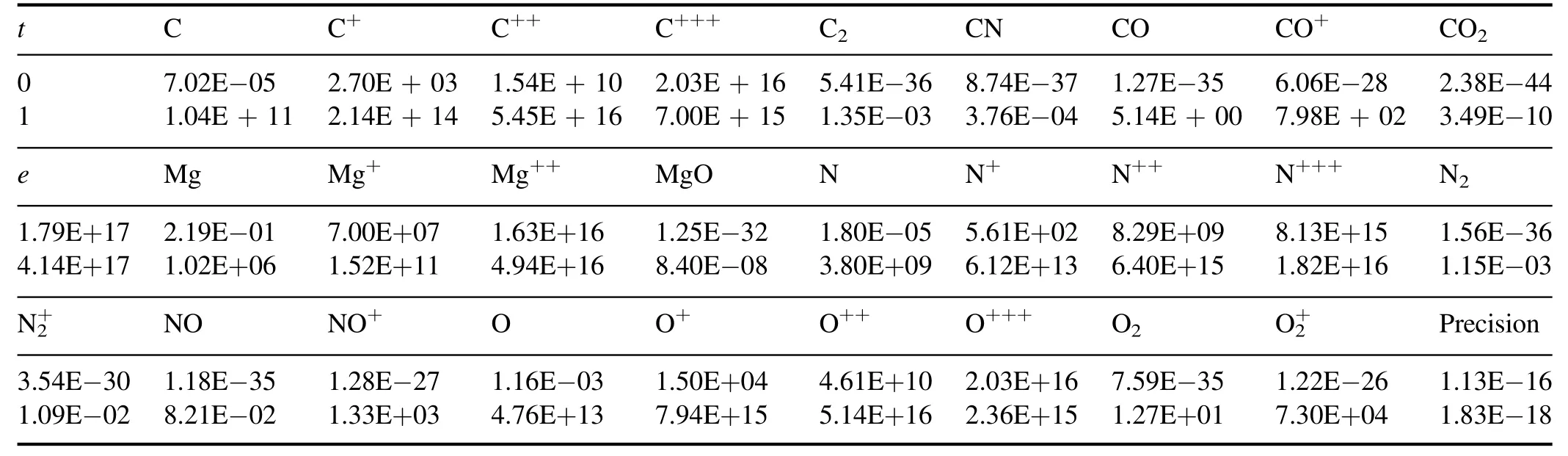
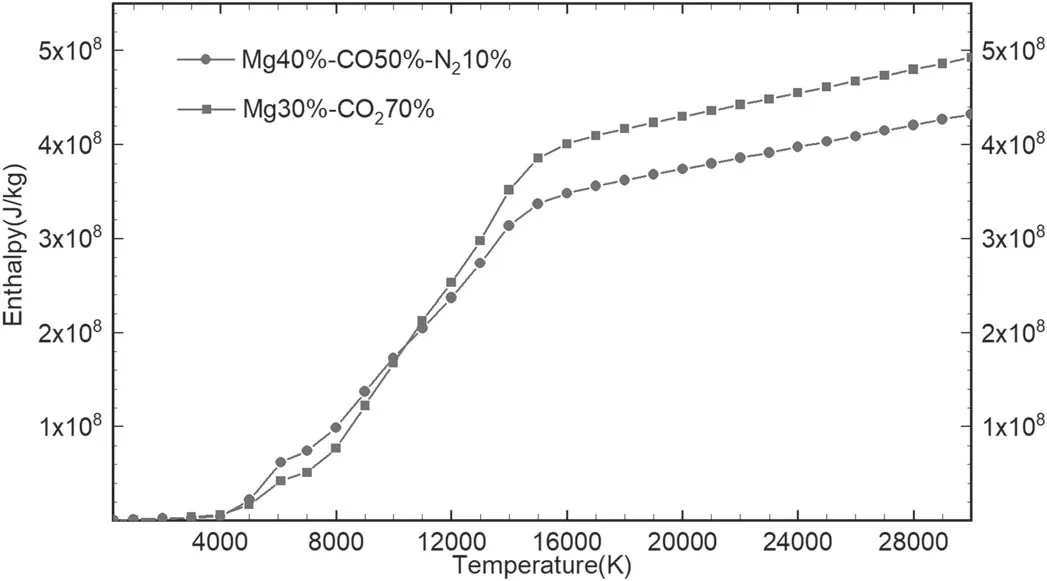
where H(x,t) represents the homotopy equations,tis the homotopy sequence factor, F(x) represents the solving equations, and G(x) represents the auxiliary equations that need to be constructed or assigned.Ift=1, H(x,t)=G(x),and ift=0, H(x,t)=F(x).Essentially, the process of the HAM method in dealing with equations is to conduct the transformation from H(x,1)=G(x) to H(x,0)=F(x) by solving a series of homotopy equations H(x,tk),wheretkis thekth homotopy sequence factor and 0 For the plasma composition model, there is a common sense conclusion that only the highest-valence atomic cations and electron are present in plasma at a higher temperature such as 30 000 K.The common sense conclusion can also be used as the initial value of the iterative methods and the solution satisfying requirements can be obtained through the iterative process.Hence, equations at a higher temperature were chosen as the auxiliary equations.Such equations had the advantages of a highly precise solution and the same structure as solving the system at any temperature.If the solution at one temperature can be obtained, we can have solutions at any temperature below that temperature via the HLMA.The homotopy equations can be expressed as where FTmax(x) represents the plasma composition equations at a higher temperature.The data array corresponding to the number densities of electron and the highest-valence atomic cations is existing or nonzero and all those corresponding to the number densities of other particles are equal to zero or do not exist.This data array serves as a reasonable initial value for iteration and calculation of the exact solution of the auxiliary equations by the LMA.Otherwise, we can only reconstruct the auxiliary equations by raising the temperature ofTmaxsuch asTmax=Tmax+2000.Every homotopy equation is still in a singular nonlinear system that cannot be solved analytically.However,the LMA can easily solve these equations if a reasonable initial value is given.When the ratio of HT(x,tk−1)/HT(x,tk) is close to 1, the solution of HT(x,tk−1)can be used as the initial value of HT(x,tk).In this way,we achieved the combination of the homotopy method and LMA where the homotopy method determined the homotopy equations by adjustingtkand the LMA solved these equations. Another key factor of the HLMA is to determine the control parameter sequence [tk] such as 0=t0 The last solution can be obtained byNtime iterations of the LMA calculation,whereNis the number of the homotopy step.The equations of HT(x,tk) are also singular nonlinear equations.For a given plasma, the maximum value occurs in a fixed chemical reaction that does not vary with temperature and is marked asSa,max.Sa,maxis the maximum singular value and this reaction is the maximum singular traction.Similarly,the maximum singular valueSt,maxof the solving equation can be obtained from the same reaction.In this paper, the ratioRmaxof the maximum singular coefficientSa,maxof FTmax(x)=0 toSt,maxof FT(x)=0 was selected as the reference value to determine the control parameter sequence[tk].In regard to the homotopy step number,the larger number is the better in principle.Hence,we selectedN=(Tmax−T)/50 in the initial period in this paper.When using the LMA algorithm to solve HT(x,tk) =0, it is necessary to calculate the Jacobian matrix J.J is calculated by The element is calculated by In the actual calculation,ifxjis not equal to 0,dx=1e–5 ×xj; else dx=1e – 5. The control parameter sequence[tk]is constructed via the equal-scale model, and the proportionality coefficientqand the homotopy coefficienttkare expressed as wheretk=1 whenk=0 andtk=0 whenk=N.Whenkis small, the difference oftk−tk−1is large, and with the increase ink, this difference gradually decreases.The step numberNis the key parameter to adjust the homotopy sequence so that each step of LMA calculation can be completed successfully.If LMA fails,Nmust be dynamically adjusted to reduce the difference oftk−tk−1to make sure that the solution of HT(x,tk−1) will be a reasonable initial value for HT(x,tk).This process is iterated until the whole homotopy process is accomplished.In this paper,Nais defined as the number of successful solutions by the LMA.When theNa+1 LMA calculation fails, ifNa<10,Nis reset toN+Na; else,Nis reset toN—Na/2.The proportionality coefficientqis calculated as follows: The values ofqandtkare recalculated by equations(23)and (24).The purpose of adjusting step N is to reduce the number of LMA calculations and avoid wasting computing resources.. Figure 1.Calculation flow chart of the HLMA for solving the plasma composition. The procedure of the HLMA can be divided into two parts that are executed successively.The first part is to construct and solve the auxiliary equations,and the second part is to adjust the step numberNand achieve the solution of a series of homotopy equations by the LMA; the conditions of convergence of the LMA are||F|| The calculation process of the HLMA is shown in figure 1 and the detailed procedures for solving the plasma composition model are as follows: (1) Determine the maximum temperatureTmaxand homotopy step numberNmaxand construct the auxiliary equations G(x);set the calculation accuracyepsand setNa=0,tc=0 at the same time. (2) Assuming that only electrons and the highest-valence atomic cations exist in the plasma, construct and solve the linear equations containingNe+ 1 variables according to the law of charge conservation, Dalton’s law of partial pressure,and the assumption that the ratio of the total number densities of atoms is constant; then the exact solution or a reasonable iterative initial value under the assumption is obtained. (3) Solve the auxiliary equations and obtain their variancep.Ifp (4) Find the maximum singular valuesSa,maxof the auxiliary equations andSt,maxof the solving equations,and calculateRmax=Sa,max/St,max. (5) Calculate the proportional coefficientqand setk=0. (6) Compute the homotopy coefficienttkand construct the homotopy equations H(x,tk). (7) Solve the homotopy equations H(x,tk) by the LMA,with two conditions of convergence: (a) ||F|| The physician s failure to recognize that he is subordinate to his godfather, and that despite his privileged position as godson he too is mortal, leads to his downfall. Note that he is not satisfied with wealth and power, but now strives to marry a princess and win a crown. What is considered a legitimate30 goal in tales of magic becomes a mark of hubris31 in this tale. (198) (8) Calculate their variancep.If notp (9) IfNa<10, setNmax=Nmax+Na.Otherwise, setNmax=Nmax—Na/2,Rmax=(1 −tc)Rmaxand go to step 5. (10) If notk=Nmax, setk=k+1,tc=tkand go back to step 6.Otherwise, go to step 11. (11) Finished. According to the above statement, the HLMA can be used to solve the plasma equilibrium composition at arbitrary temperatureT,number of atomic elementsNe,and total pressureP.Three example cases are selected whereT=6000 K,P=0.1 MPa,Ne=2, and auxiliary temperatureTmax=7000 K in Case 1;T=10 000 K,P=0.1 MPa,Tmax=30 000 K, andNe=3 in Case 2; andT=12 000 K,P=0.1 MPa,Tmax=30 000 K, andNe=4 in Case 3.The computational accuracy ||F||<1e−10.They are used to demonstrate the accuracy and feasibility of HLMA for the plasma equilibrium composition model. Case 1: Mg(30%)–CO2(70%) mixture plasma, temperatureTe=10 000 K, and auxiliary temperatureTmax=30 000 K.There are 19 particles and 15 chemical reactions considered for this plasma, including eight neutral particles,ten ions and five dissociation reactions, and ten ionization reactions.These particles contain one triatomic molecule and four diatomic molecules,and the other particles are electrons,monatomic molecules and their ions.Table 1 shows the list of molecules in the plasma.The possible chemical reactions are listed in table 2,and table 3 lists the solutions for the solving equations (t=1) and the auxiliary equations (t=0).It can be seen that the values of some solutions vary greatly,such as CO; the value of the solution changes from 1.43e−35to 8.79e6, with the difference reaching 41 orders of magnitude.A total of 710 homotopy calculations were carried out. Table 1.List of molecules in the Mg–CO2 mixture plasma. Table 2.List of possible chemical reactions in the Mg(30%)–CO2(70%) mixture plasma. Table 3.Solutions of auxiliary and solving equations for the Mg(30%)–CO2(70%) mixture plasma. Table 4.List of molecules in the Mg(40%)–CO(50%)–N2(10%) mixture plasma. The variations of the control parameter, the precision,and the number density of each particle with the homotopy step number are shown in figure 2.It is found that the transition from the auxiliary solution to the exact solution is a continuous and smooth gradual process.The fluctuation of the control parametertkchanges from violent to gentle and finally becomes close to zero.Hence,we can judge that the precision of each HLMA step meets the calculation requirements. Figure 2.Variations of the control parameter,the precision,and the number density of each particle with the homotopy step number for the Mg(30%)–CO2(70%) mixture plasma. Table 6 gives the solutions of the auxiliary function(t=0)and the solution function (t=1)in the calculation of Case 2.The solution accuracy of the auxiliary function ||F||=1.13e−16,and the solving function solution precision||F|| = 1.83e−18, which is better.A total of 362 HLMA calculations were performed during the calculation, and the variations of the control parameter, the precision, and the number density of each particle with each LMA are shown in figure 3.At this temperature, the number densities of the polyatomic molecules are less than 1 cm−3.It can also be seen that only electrons, atoms, and their ions exist in the plasmaand there are no polyatomic molecules when the temperature is higher, which is consistent with our assumption for determining the auxiliary equations. Table 5.List of possible chemical reactions in the Mg(40%)–CO(50%)–N2(10%) mixture plasma. Table 6.Solutions of auxiliary and solving equations for Mg(40%)–CO(50%)–N2(10%) mixture plasma. Table 7.List of molecules in the N2 plasma. Table 8.List of possible chemical reactions in the N2 plasma. Table 9.Solutions of the auxiliary and solving equations for the N2 plasma. Figure 3.Variations of the control parameter,the precision,and the number density of each particle with the homotopy step number for the Mg(40%)–CO(50%)–N2(10%) mixture plasma. Case 3: pure N2plasma, temperatureTe= 6000 K and auxiliary temperatureTmax= 7000 K.The auxiliary temperature of this example is 7000 K, which is not consistent with the so-called higher temperature,but it is possible to calculate the equilibrium compositions if we have number densities that are higher than the calculated temperature.The lists of molecules and reactions for pure N2are shown in tables 7 and 8, respectively.The values of equilibrium compositions atT=7000 K andT=6000 K have been listed in table 9.In the cases ofT=6000 K orT=7000 K,the reaction N⇌N++e is dominant in the plasma, and the numbers of N++, N+++and N2+are very few.In figure 4, the number densities of electrons and N+particles appear to coincide. It can be seen from the above figures that the control parameters vary from 0 to 1.With the progress of thehomotopy process, the difference between adjacent control parameters decreases gradually, and the minimum value reaches 1e−10.The change of control parameters ensures the continuity of the homotopy process.In the process of calculation, each variable is continuously transitioning from the initial value to the final solution, which ensures the correctness of the iterative direction.The most important factor is that there is no need to worry about the calculation process falling into the local optimum and being difficult to escape.In the HLMA calculation, if the local optimum is trapped, the step size of control parameters can be adjusted appropriately,and the LMA can jump out of the local optimal solution by automatically adjusting the range of the trust region.This is also the advantage of the HLMA algorithm to solve nonlinear problems, which can not only ensure the correctness of the optimization direction but also escape from the local optimal region smoothly. Figure 4.Variations of the control parameter,the precision,and the number density of each particle with the homotopy step number for the N2 plasma. In the process of batch calculation, it is not necessary to select an auxiliary function at a higher temperature, such as 30 000 K,as long as the temperature is higher than the current solution under the same pressure.In the practical application process, the author summed up an immature experience, and suggested that ifT> 15 000 K, thenTmax–T=1000 K; ifT>8000 K, thenTmax–T=500 K; ifT>5000 K, thenTmax–T=100 K;ifT>3000 K,thenTmax–T=50 K;elseTmax–T=10 K.These suggestions can effectively shorten the gap between the auxiliary equations and the solving equations, ensure that the solving variables are in a controllable range, and also greatly reduce the number of homotopy calculations, providing work efficiency. In this paper,the equilibrium composition number densities are calculated in the temperature range of 300–30 000 K for pure N2, Mg(30%)–CO2(70%) and Mg(40%)–CO(50%)–N2(10%)mixture plasmas at atmospheric pressure;the calculation results are shown in figures 5–7.It can be seen from the figures that the main particles of plasma at higher temperature are electrons and the highest atomic cations(e,C3+,O3+,Mg2+,N3+),and it is shown that polyatomic molecules are completely decomposed and monatomic molecules are deeply ionized.This conclusion also proves the correctness of choosing equilibrium compositions at higher temperatures as the auxiliary function.With the decrease of temperature, low-order atomic cations gradually appear until the monatomic molecules are precipitated, and the value of number density increases rapidly.Molecular ionization and dissociation reactions are dominant at lower temperatures.In the actual calculation process, in order to reduce the amount of calculation,the plasma temperature as an auxiliary function can be solved by the HLMA algorithm as long as it is higher than the solution, rather thanTmax=30 000 K as shown in Case 3.Here, the authors make an empirical conclusion, the calculation precision of the auxiliary function||F||<1e−10,which can effectively reduce the number of LMAs.The equilibrium compositions of pure N2at temperatures of 300–3000 K and pressure of 0.1 MPa are displayed in figure 8.We found that the composition proportion of N2+is obviously higher than in the case of θ=1, and the larger θ, the greater the proportion. Figure 5.Equilibrium compositions of Mg(30%)–CO2(70%) mixture plasma at temperatures of 300–3000 K and pressure of 0.1 MPa.(a)300–8000 K, (b) 8000–30 000 K. Figure 6.Equilibrium compositions of Mg(40%)–CO(50%)-N2(10%) mixture plasma at temperatures of 300–3000 K and pressure of 0.1 MPa.(a) 300–8000 K, (b) 8000–30 000 K. In these calculations, other producing polyatomic molecules are considered, such as O2, C2, CO2, MgO, NO, CN,and CO.At the same time, the ionization reaction of an O2molecule with a strong oxidation property is also considered.The calculation of the partition function takes into account the various electronic states of the molecule, which effectively improves the accuracy of the composition number density,and is especially important for the calculation of spectral data.The electronic state energy level data of monatomic molecules are obtained from the NIST Atomic Spectra Database[29].For CO,the electronic states X1Σ+,A1Π and B1Σ+are mentioned, and their spectral data come from Farrenq [30],Ostrowska [31] and Eidelsberg [32], respectively.For CO+,X2Σ+[33], A2Πi[33], B2Σ+[34] and C2Δ [35] electronic states are used to calculate.For O2[36]and O2+[37],we refer to X3Σ−g,B3Σ−utwo states and X2Πg, a4Πg, A2Πg, b4Σ−gfour states.C2have eight electron states are obtained from Kirby[38], and the four electronic states MgO have been found from the NIST-JANAF thermochemical tables [39].For CN,X2Σ+, A2Πi, and B2Σ+three electronic states have been taken into account; the spectral data are available from Peteret al[40].For NO, the electronic states of X2Πr, A2Σ+and D2Σ+are given by Reddy [41], and the states of B2Σrand C2Πrare referred to[41].The spectral data of the X1Σ+state for NO+have been listed by Peteret al[40].The calculations of the partition function for CO2have been discussed by Grayet al[42]; only the vibrational level of the ground state is considered in this paper, and the vibrational constants are 2349 cm−1, 1337 cm−1and 667 cm−1(2). Figure 7.Equilibrium compositions of pure N2 at temperatures of 300–3000 K and pressure of 0.1 MPa.(a)300–8000 K,(b)8000–30 000 K. Thermodynamic properties (including density, enthalpy, etc)are important conditions for calculating the temperature of a system according to the law of conservation of energy, and they are also the basis for calculating the temperature field in computer aided engineering (CAE).When the equilibrium composition number density and particle partition function are known, the mass density and enthalpy can be calculated by equations (14) and (16).For pure N2, the results for mass density and enthalpy are in good agreement with data reported by Colomboet al[14].The comparisons are shown in figures 9 and 10.For the Mg–CO2and Mg–CO–N2mixture plasmas, there are no comparable calculations, and their calculations are shown in figures 11 and 12. With the increase of temperature, the thermal motion behavior of particles becomes more active, and the force on the boundary becomes stronger.Under the same pressure,the total number density of plasma decreases.At the same time,the energy level of the particle jumps from the ground state to the excited state, which enlarges the internal energy and partition function of the particle.As the internal energy of the molecule enlarges, the enthalpy of the plasma also increases,and the energy density of the unit volume of the plasma becomes higher.Due to the small volume of arc plasma in industrial applications, the time and energy required to raise the plasma temperature are far less than those of conventional fossil energy, which also lays the foundation for the application of high-temperature and ultra-high-temperature plasma. Figure 9.Comparison of mass density in N2 plasma at temperatures of 300–30 000 K and pressure of 0.1 MPa.The literature result was calculated by Colombo et al [14]. Figure 10.Comparison of enthalpy in N2 plasma at temperatures of 300–30 000 K and pressure of 0.1 MPa.The literature result was calculated by Colombo et al [14]. In this paper,an equilibrium plasma composition model under local thermodynamic nonequilibrium conditions was established by the Saha and Guldberg–Waage equations combined with the mass conservation equation,the charge conservation equation, and Dalton’s law.The homotopy Levenberg–Marquardt algorithm(HLMA)was proposed for the first time and used to solve the plasma composition model.The main conclusions are as follows. The auxiliary equations constructed at a higher temperature could be accurately solved by the LMA and the initial value was chosen according to the assumption that the number density ratio between electrons and the highestvalence atomic cations is constant. The HLMA could solve the singular nonlinear equations when the auxiliary equations were obtained and the difference in values oftk−tk−1between two adjacent control parameters was small. HLMA could solve the plasma composition model at arbitrary temperatures and arbitrary thermal nonequilibrium parameter θ, number of atomic elements, and pressure with high accuracy and convergence of the homotopy process.The calculation accuracy of three examples is ||F||<1e−12. Figure 11.Mass density of Mg(30%)–CO2(70%)and Mg(40%)–CO(50%)–N2(10%)mixture plasmas at temperatures of 300–30 000 K and pressure of 0.1 MPa. Figure 12.Specific enthalpy of Mg(30%)–CO2(70%)and Mg(40%)–(CO50%)–N2(10%) mixture plasmas at temperatures of 300–30 000 K and pressure of 0.1 MPa. Acknowledgments This study was supported by the National Key Research and Development Program of China(No.2017YFA0700300),the Fundamental Research Funds for the Central Universities(No.N2025032),and the Liaoning Provincial Natural Science Foundation (No.2020-MS-362). ORCID iDs3.2.Solution of auxiliary equations and construction of homotopy equations
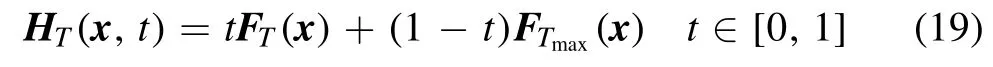
3.3.Determination of the homotopy sequence
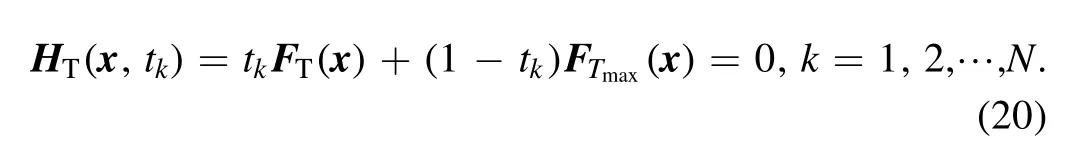
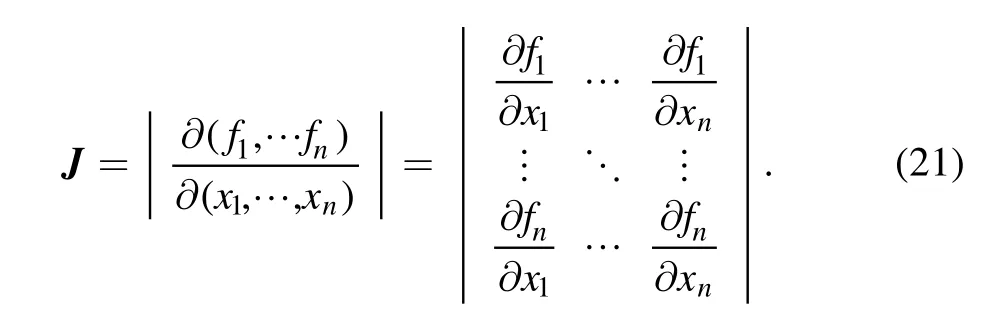
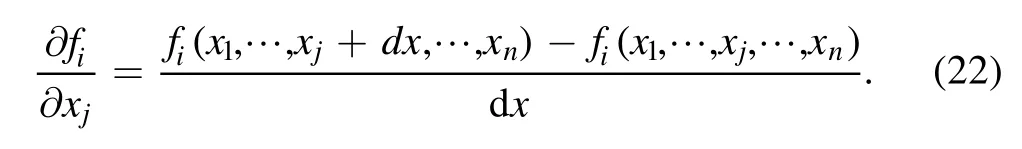
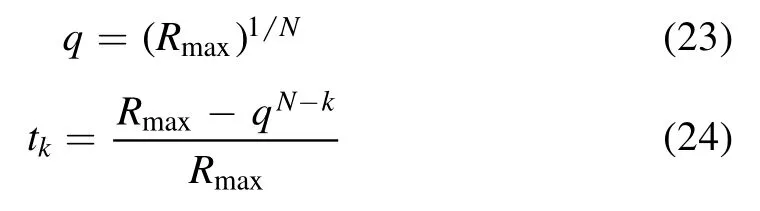
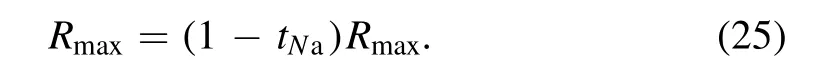
3.4.Procedure of the HLMA
3.5.Cases
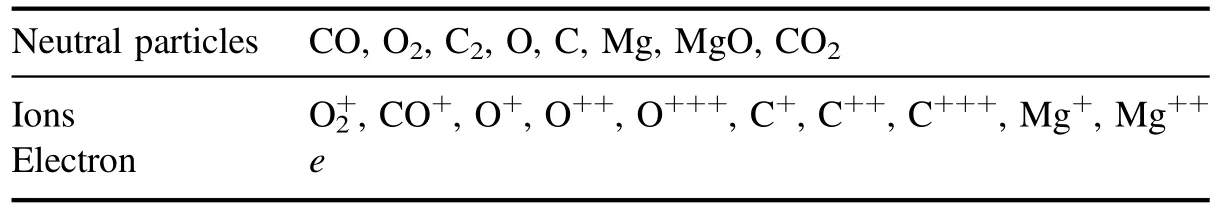
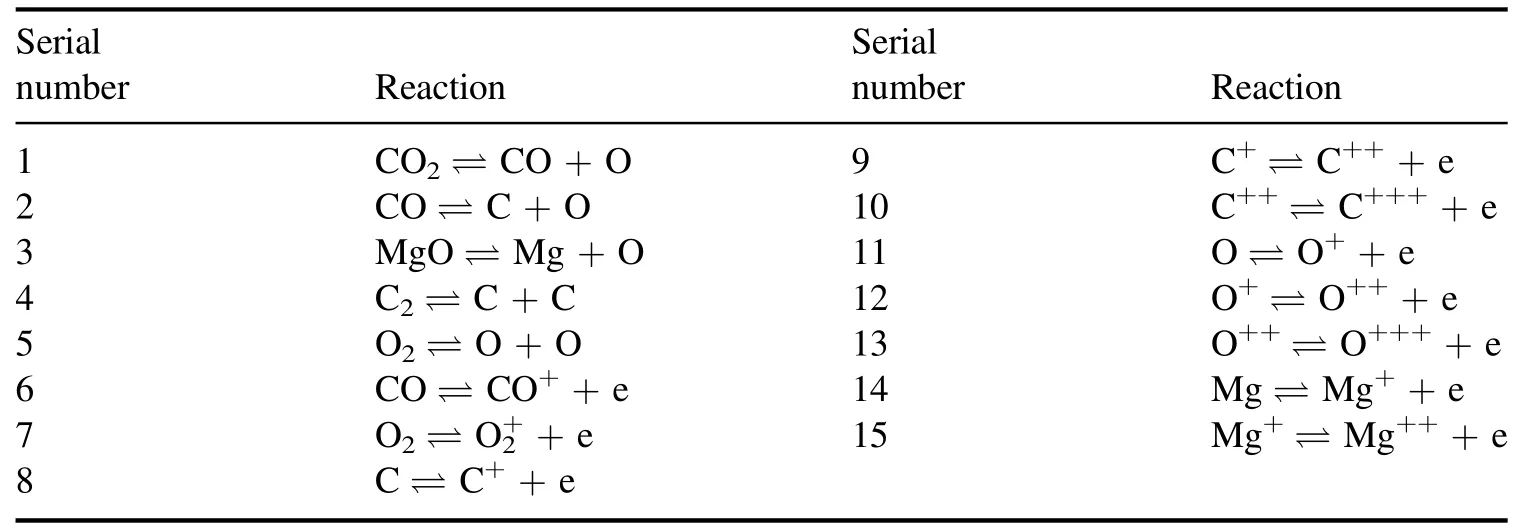
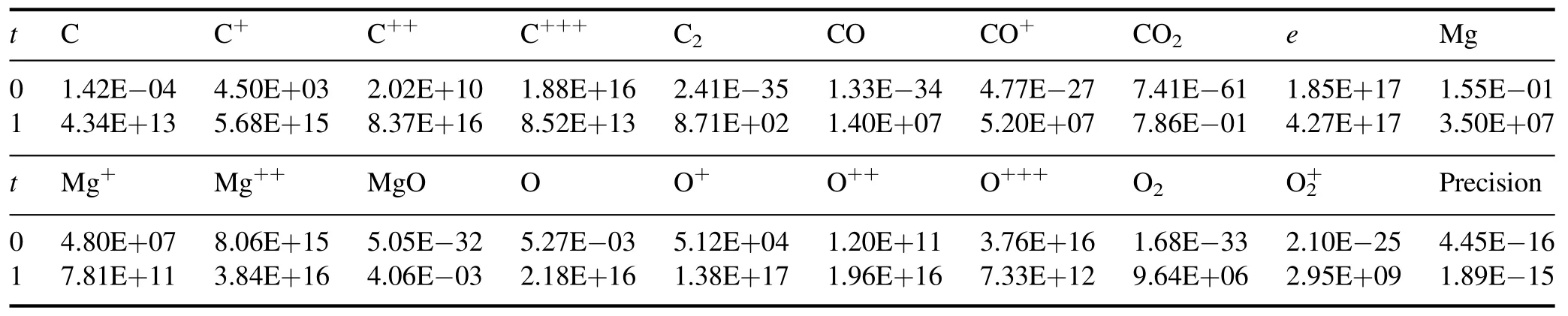
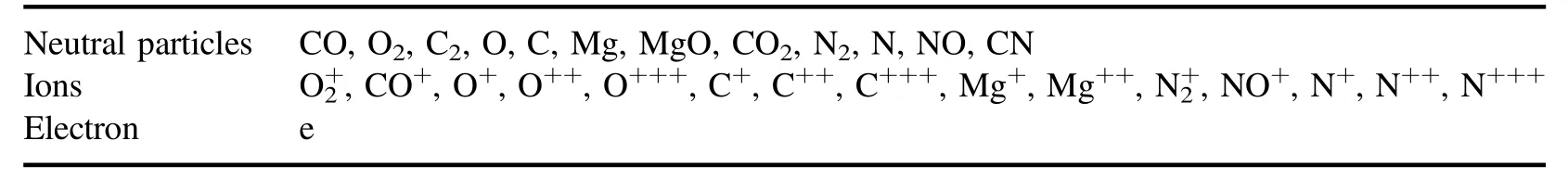



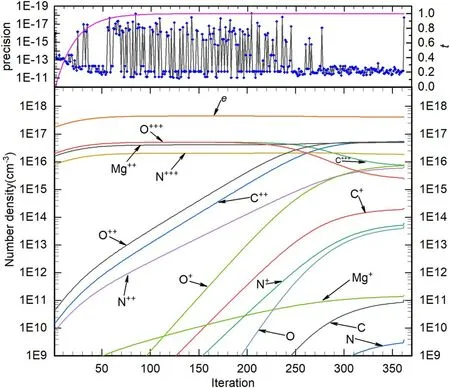
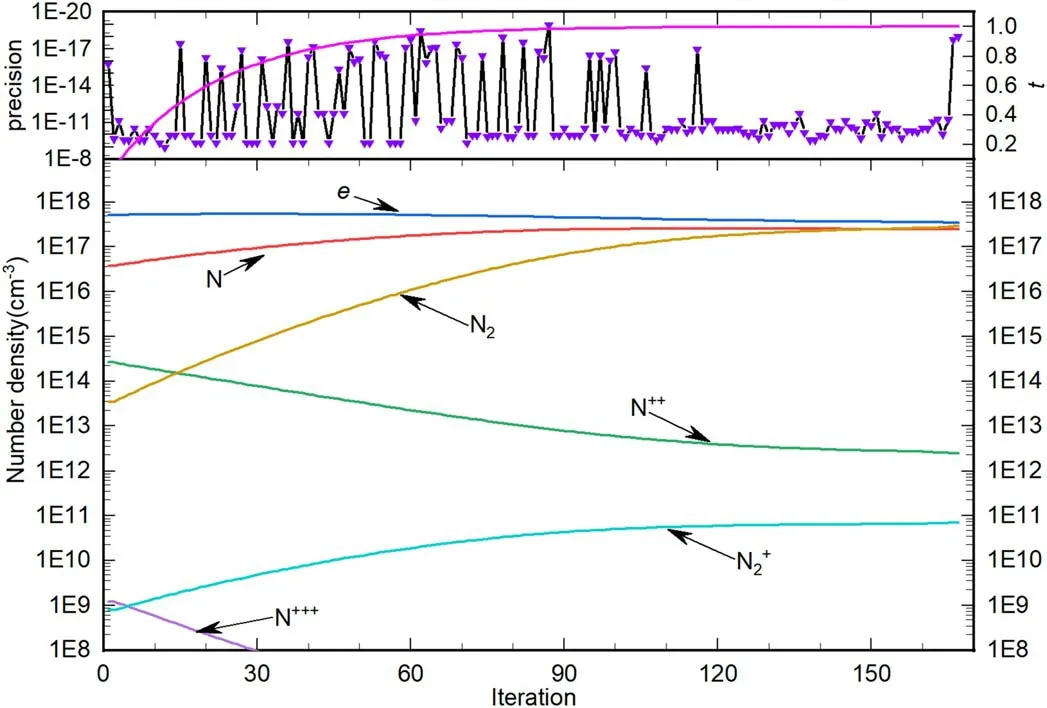
4.Results and discussion
4.1.Equilibrium composition

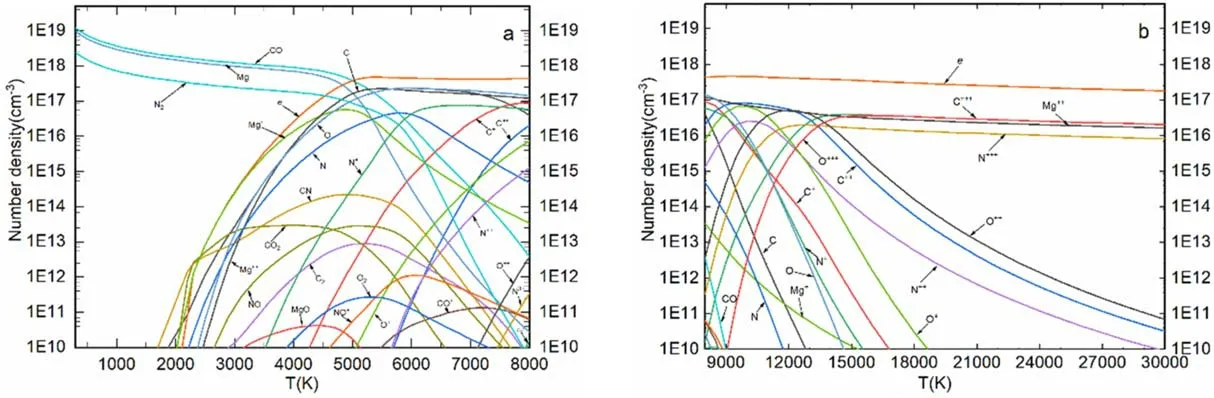
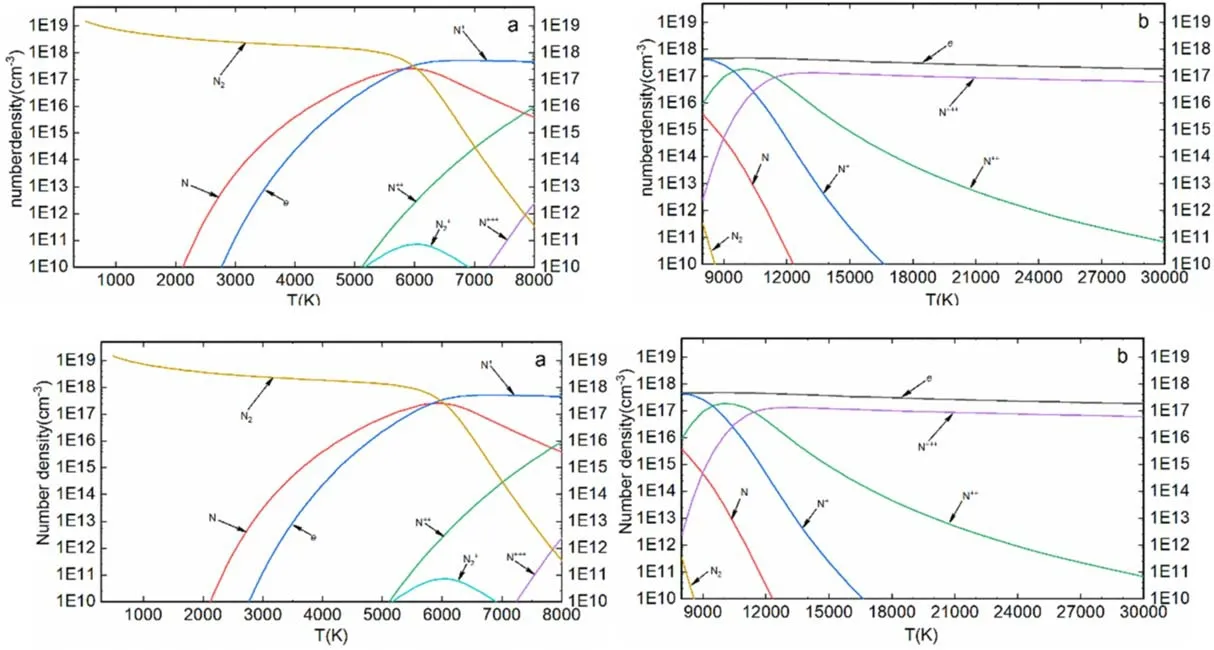
4.2.Thermodynamic properties


5.Conclusions
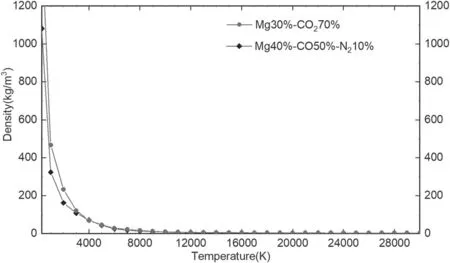
 Plasma Science and Technology2021年12期
Plasma Science and Technology2021年12期
