The propagation dynamics and stability of an intense laser beam in a radial power-law plasma channel
Xueren HONG (洪学仁),Desheng ZHANG (张德生), Jiming GAO (高吉明),Rongan TANG (唐荣安),∗, Peng GUO (郭鹏) and Jukui XUE (薛具奎)
1 Key Laboratory of Atomic Molecular Physics&Functional Materials of Gansu Province,and College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,Peopleʼs Republic of China
2 School of Mathematics and Physics,Lanzhou Jiaotong University,Lanzhou 730070,Peopleʼs Republic of China
Abstract By containing ponderomotive self-channeling,the propagation behavior of an intense laser beam and the physical conditions are obtained theoretically in a radial power-law plasma channel.It is found that ponderomotive self-channeling results in the emergence of a solitary wave and catastrophic focusing,which apparently decreases the region for stable propagation in a parameter space of laser power and the ratio of the initial laser spot radius to the channel radius (RLC).Direct numerical simulation confirms the theory of constant propagation,periodic defocusing and focusing oscillations in the parameter space, and reveals a radial instability which prevents the formation of bright and dark solitary waves.The corresponding unstable critical curve is added in the parameter space numerically and the induced unstable region above the unstable critical curve covers that of catastrophic focusing, which shrinks the stable region for laser beams.For the expected constant propagation, the results reveal the need for a low RLC.Further study illustrates that the channel power-law exponent has an obvious effect on the final stable region and laser propagation, for example increasing this exponent can enlarge the stable region significantly,which is beneficial for guiding of the laser and increases the lowest RLC for constant propagation.Our results also show that the initial laser amplitude has an apparent influence on the propagation behavior.
Keywords: laser beam, power-law channel, propagation dynamics, stability
1.Introduction
The propagation of laser beams [1, 2] has received considerable attention due to their important applications, such as plasma-based acceleration [3–10], harmonic generation[11, 12], x-ray lasers [13, 14] and advanced laser fusion schemes [15].A laser beam can propagate in a vacuum by about a Rayleigh length due to natural diffraction.For the above applications, however, more than several Rayleigh lengths are required.Propagation in a plasma may effectively increase the traveling distance.In a uniform plasma, the laser suffers relativistic self-focusing, which can overcome natural diffraction and ensure a long propagation distance if the laser power is larger than a critical value.When the laser power is smaller than this critical value, however, relativistic selffocusing fails to prevent diffraction and other focusing methods are needed.A preformed plasma channel is an effective technique for providing a powerful focusing effect and can play the role of a waveguide tube [7]; preformed plasma channels are widely used for laser guiding in related works.
As we know,preformed channels are usually designed to be parabolic in the radial direction[7,16,17].Other channels have previously received less attention than the usual parabolic channel.Nevertheless,some special advantages have been reported for non-parabolic channels.For example, a class of Raman-type instabilities may be stabilized in a leaky density channel[18,19]and good stable laser transmission with high quality in inhomogeneous plasmas can be achieved in a hollow channel[20–25].In addition, recent work on the development ofq-Gaussian, super-Gaussian and quadruple Gaussian lasers [26–32] may inspire investigation of laser guiding in non-parabolic channels.In experiments, various channel structures can be achieved by controlling some of the experimental parameters [4, 7, 33–35].Therefore,the investigation of laser propagation in non-parabolic channels is necessary and crucial.Quasi-matched propagation of laser pulses in a plasma channel with a general radial profile has recently been studied [36].Attention to the corrugated channel has revealed rich laser beam behaviors, such as aperiodic oscillation, resonance, beat-like waves and periodic oscillation with multipeaks[37].Our recent work on laser propagation in a radial power-law channel [38], which is a reasonable and general extension of a parabolic density channel, has revealed that constant propagation is sensitive to the power-law exponent.
In preliminary work [38] on radial power-law plasma channels, however, ponderomotive self-channeling was not considered because of the difficulty of theoretical analysis.Ponderomotive self-channeling is related to the ponderomotive force, which can be viewed as the radiation pressure, i.e.the gradient of the electromagnetic energy density [7].Under the action of this force, electrons are expelled transversely away from regions of high laser intensity in the long pulse length limit and ponderomotive self-channeling emerges.Previous studies on ponderomotive self-channeling[39–41]in parabolic channels revealed a more complex parameter space than in[38].After comparisons, it can be found that ponderomotive self-channeling can result in a parameter region for catastrophic focusing, and apparently decreases the traditional propagation domain in parameter space for a parabolic channel.Therefore,for an investigation into a radial power-law channel ponderomotive self-channeling must be contained.
After some effort we overcame the theoretical difficulty of treating ponderomotive self-channeling in a radial power-law plasma channel and developed the theory presented in this work.Meanwhile, we also investigated the propagation dynamics by direct simulation of the wave equation with the finite difference method.The laser behaviors and their physical conditions are analyzed.As expected, ponderomotive self-channeling induces the emergence of solitary waves and catastrophic focusing,which obviously decreases the area for stable laser propagation.Some interesting findings were obtained.(1) Theoretical results indicate that the increase in the channel power-law exponent may dramatically decrease the domain for catastrophic focusing and be conducive to laser propagation.(2) Direct numerical simulation confirms the theory of constant propagation,periodic defocusing and focusing oscillations in parameter space, and reveals a radial instability which prevents the formation of bright and dark solitary waves.We added the corresponding unstable critical curve to the parameter space numerically and the induced unstable region above the unstable curve covers that of catastrophic focusing, which further shrinks the stable region for laser beams.(3) For the usually expected constant propagation,the results reveal the need for a lowest RLC(ratio of the initial laser spot radius to the channel radius).(4) Increasing the channel power-law exponent can enlarge the final stable region significantly and also increase the lowest RLC for constant propagation.It should be noted that findings(2)and(3)recover the previous knowledge even for the case of a parabolic channel,such as in a previous study of solitary waves [39] and other studies associated with constant propagation.Our studies also demonstrate the obvious effects of the initial amplitude of the laser on the propagation behavior.These findings are important for the guiding of lasers and other related applications.
This paper is organized as follows.The basic model and evolution equations are given in section 2.The propagation types and characteristics are obtained theoretically in section 3.Numerical simulation of the wave equation and further analysis are done in section 4.A summary is provided in section 5.
2.Basic model and evolution equations
Taking into account ponderomotive self-channeling and the weakly relativistic limit (|a|2≪1, where a is the normalized vector potential and its normalization is presented after equation (2)), an intense laser beam propagating in an underdense plasma (n/nc<1, wherenis the density of the underdense plasma andncis the critical density) is described by the following two equations [40–44]:

where a(r,z,t) is the vector potential and is normalized bym0c2/e,m0andeare the electron rest mass and charge,respectively,cis the velocity of light in a vacuum,ωp=(4πn0e2m0)12is the plasma frequency and δnis the perturbed electron density.n(r) denotes the power-law density channel

wheren0is the initial axial density of the electron,rchis the channel radius andd>0 is the power-law exponent.Whend=2,equation(3)is reduced to the familiar parabolic case.The Coulomb gauge ∇·a=0 is adopted in deriving equations (1)and (2).Obviously, equation (1) is the wave equation for the laser field and equation (2) describes the perturbed electron density associated with the excitation of the wakefield.For simplicity, we consider the dynamics in the long pulse length limit ωpτl≫1,with τlthe laser pulse width.Thus,equation(2)is simplified as [40]
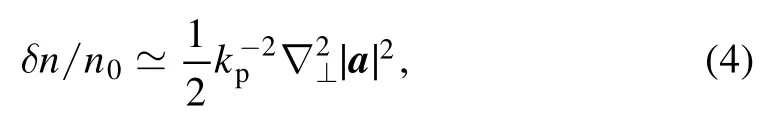
wherekp=ωp/crepresents the plasma wave number.Equation (4) shows the formation of ponderomotive self-channeling [7], which was ignored in our earlier work [38] for simplicity.
Here, we study a circularly polarized laser beam propagating along thezdirection in a plasma.So, the form of the vector potential is set as
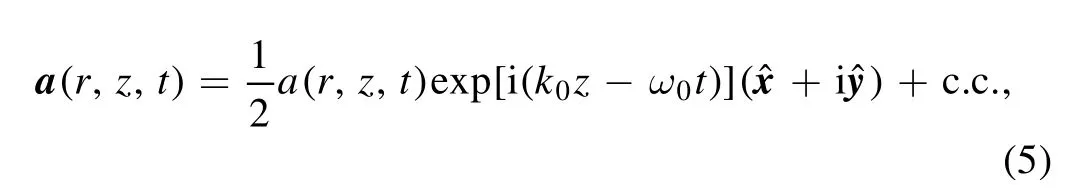
wherea(r,z,t)represents a complex slowly varying envelope,ω0represents the laser center frequency,k0=vgω0/c2represents the wave number of the laser center,vgrepresents the laser group velocity and ˆxand ˆyare unit coordinate vectors;c.c.is the complex conjugate.
By using equations (3)–(5) and the coordinate transformationz=z, τ=t−z/vgwith paraxial treatment and the slowly varying envelope assumption |∂a/∂τ|≪|ωpa|,equation (1) is changed to
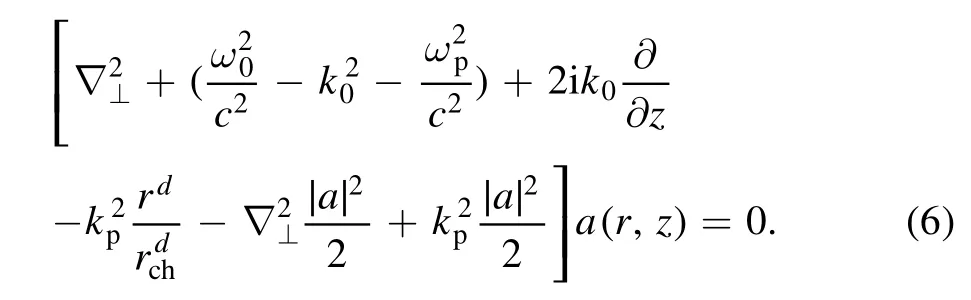
In equation (6), the fifth term is caused by ponderomotive self-channeling.Without this term, equation (6) reduces to equation (4) in [38].Settingd=2 corresponding to the parabolic case and adopting the assumption of the linear dispersion relationequation (6) is simplified to become equation (3) in [39] and equation (5)in [40].
To get the solution to equation (6), we adopt the following trial function:

wherear,rs,band φ represent the amplitude, spot radius,spatial chirp parameter and phase shift of the laser beam in plasmas at any distancez, respectively.By applying the variational method [38, 40, 41, 44–46] to equation (6), one can obtain the following equations forar,rs,band φ:


3.Propagation types and characteristics
Equation (8) shows thatas2rs2=a02r02, witha0being the initial (z=0) laser amplitude andr0the initial laser spot radius.Usingarrs=a0r0and combining equations (9) and(10), the normalized evolution equation of the laser spot radius becomes

Integrating equation (12) with the initial conditionrs|z=0=1 and drs/dz|z=0=0, one obtains

where the expression for the Sagdeev potential is

with

The form of equation (13) is similar to the energy conservation equation for a particle with ‘timez’ and ‘positionrs’.Thus, we can investigate equation(13)by analyzing the Sagdeev potential.
To get the features of the Sagdeev potential,we begin with the investigation of the two equationsV(rs)=0 andV′ (rs)=0.For the parabolic case, it is easy to list the roots ofV(rs)=0[40, 41, 44], so that one can get the propagation characteristics directly.However, it seems that there is no algebraic theory to give their roots directly for a generald.Nevertheless,we can get some important properties of the roots under the appropriate conditions 0
(1) forV(rs)=0, the value 1 is one root and there are at most two other positive roots
(2)V′(rs)=0may have no positive root,one positive root or two positive roots.
According to the two properties, considering the asymptotic behaviors ofV(rs), i.e.V(rs)→∞whenrs→∞ andV(rs)→−∞whenrs→0, the qualitative figures of the Sagdeev potential aroundV(rs)=0 can be drawn as in figure 1,which includes nine kinds of profile.Figures 1(a)–(c)correspond to the case of three roots ofV(rs)=0.Figures 1(d)–(g)represent the case when there are two roots.Figures 1(h)and(i)are for the case of only one root.For the one-root case,it should be mentioned that there may exist other profiles besides figures 1(h) and (i).However, it is not necessary to investigate these other mathematical profiles because the basic physical behaviors in the one-root case are adequately included in figures 1(h) and (i).

Figure 1.Diagram of V(rs) around V(rs)=0.Parts (a), (b) and (c)correspond to the case when there are three roots of V(rs)=0.Parts(d), (e), (f) and (g) correspond to the case of two roots of V(rs)=0.Parts(h)and(i)correspond to the case of only one root.The marked dots represent the initial position of a test particle with rs|z=0=1 and drs/dz|z=0=0.
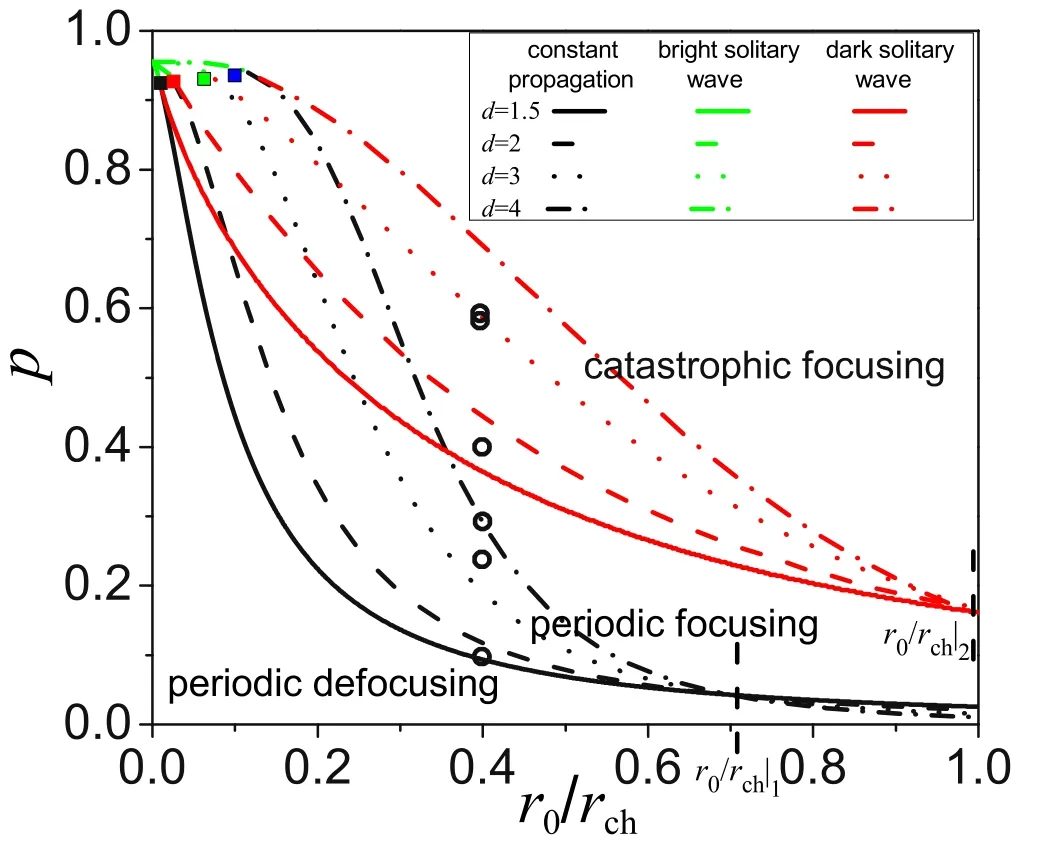
Figure 2.Parameter regions of laser propagation types.The black,green and red curves represent the conditions for constant propagation, bright solitary wave and dark solitary wave respectively.The dashed curves are for d=2 and the types of curves for other d values are labeled in the figure.For a fixed d, the areas beneath the green and black curves, between the black and red curves, and above the green and red curves correspond to periodic defocusing oscillation,periodic focusing oscillation and catastrophic focusing, respectively.The small black, red, green and blue rectangles correspond to d=1.5, 2, 3 and 4, respectively, and represent the phase transition points for the division of the parameter regions.The empty circles are parameter points used for simulation in figure 6 of section 4.Here, a0=0.3.
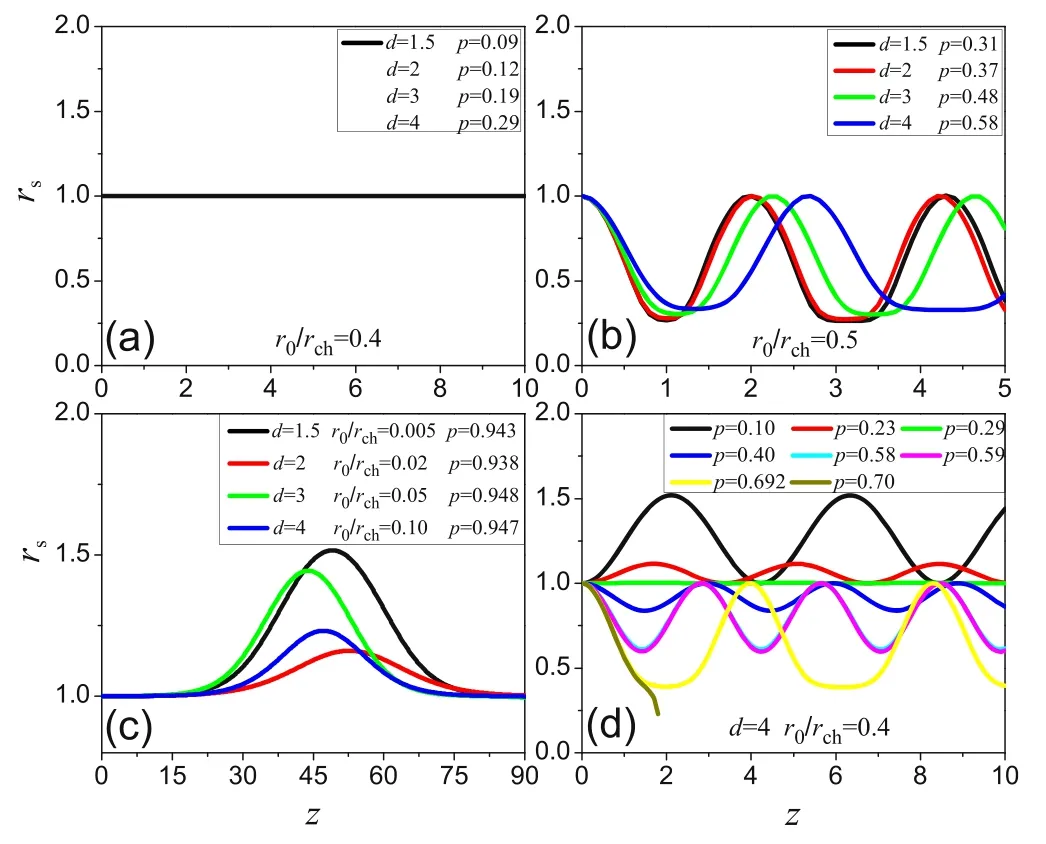
Figure 3.Display of the laser propagation types shown in figure 2.Parts (a), (b) and (c) represent constant propagation, dark solitary waves and bright solitary waves respectively.Parts (d) shows the variation of laser behavior with increase in laser power p for d=4,and it can be seen that periodic defocusing oscillation, constant propagation, periodic focusing oscillation, a dark solitary wave and catastrophic focusing may occur with the increase in p.Here,a0=0.3.

Figure 4.The effect of a0 on the parameter regions.The black,green and red curves represent the conditions for constant propagation,bright solitary wave and dark solitary wave, respectively.The dashed curves are for a0=0.3 and the types of curves for other a0 are labeled in the figure.For a fixed a0, the areas beneath the green and black curves, between the black and red curves, and above the green and red curves correspond to periodic defocusing oscillation,periodic focusing oscillation and catastrophic focusing,respectively.The small black, red, green and blue rectangles correspond to a0=0.2, 0.3, 0.4 and 0.5, respectively, and represent the phase transition points for the division of the parameter regions.The empty circle is a parameter point used for simulation in figure 9 of section 4.Here, d=4.
From figure 1, one can directly get the following propagation types and characteristics of the laser beam.
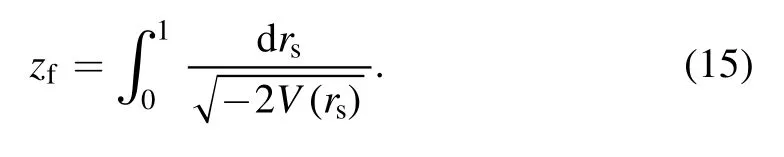
(1) Catastrophic focusing.In the cases shown in figures 1(a), (f), (h) and (i), the particle will move to the positionrs=0 considering the asymptotic behavior ofV(rs),i.e.V(rs)→−∞whenrs→0.In this case,the laser beam will catastrophically focus at the position Obviously, the pointrs=0 will never be reached because the intensity of laser will large enough to exceed the weakly relativistic limit when the laser spot radius continuously decreases.The condition of this case isV′ (rs)∣rs=1>0and ∀ra∊(0, 1),V(ra)<0 orV′ (rs)∣rs=1=0andV″(rs)∣rs=1=0, i.e.

(2) Periodic defocusing oscillation.In the case shown in figure 1(b), the motion of the particle is bounded between the positions 1 andr1, wherer1>1.It can be seen thatrs≥1 in this kind of evolution ofrs.The condition for this case isi.e.
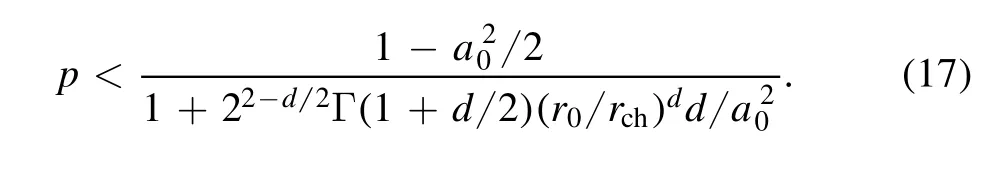
The corresponding spatial period of the oscillation is

(3) Periodic focusing oscillation.In the case shown in figure 1(c), the motion of the particle is bounded between the positionsr2and 1, wherer2<1.It can be seen thatrs≤1 in this kind of evolution ofrs.The condition of this case isV′(rs)∣rs=1>0and ∃rb∊(0,1)satisfiesi.e.

The corresponding spatial period is

(4) Constant propagation.In the case shown in figure 1(g),the particle locates at the minimum point ofV(rs), initially with with zero velocity.So the particle will stay at rest.This means that the laser spot radius does not change and the type of propagation is constant propagation.The corresponding power can be obtained by solvingV′ (rs)∣rs=1=0underV″ (rs)∣rs=1>0, which yields

with

(5) Solitary wave.In the figures 1(d) and (e), it can be concluded that the maximum pointsrs=1 in figure 1(d)andrs=r3in figure 1(e) are all saddle points by linear stability analysis.According to the corresponding nonlinear theory[44],equation(13)has solitary wave solutions in these cases.Case figure 1(d) corresponds to a bright solitary wave and the condition isV′ (rs)∣rs=1=0underV″ (rs)∣rs=1<0, i.e.
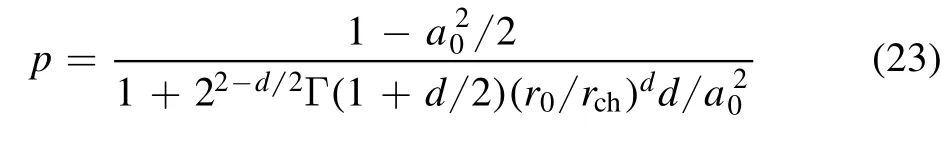
with

Case figure 1(e)corresponds to a dark solitary wave and the condition ∃r3∊(0,1)satisfeisV(rs)∣rs=r3=0,V′ (rs)∣rs=r3=0 andV″ (rs)∣rs=r3<0, i.e.

As we known,solitary waves are typical solutions for a variety of nonlinear systems, such as in the deep ocean[47], plasmas [48] and others.Here, a bright solitary wave means a single‘hump’ofrs,while a dark solitary wave represents a single‘pit’ofrs.One should note that these are quite different.
Obviously,the propagation types in this power-law density channel are very rich.Meanwhile, the condition of each propagation type strongly depends ond.To make a further study of the propagation characteristics and the channel effects, we plot the propagation characteristics map in parameter space (p,r0/rch), i.e.figure 2, in which the parameter regions corresponding to different types are classified using the above conditions.The correctness of figure 2,i.e.the above theory based on equation (12), is well verified by solving this ordinary differential equation (12) numerically and we display some of the solutions in figure 3.With the parameters presented in figure 2,the behaviors of the constant propagation, dark solitary waves and bright solitary waves are respectively shown in figures 3(a),(b)and(c)for differentd.All the above five types are displayed in figure 3(d)by settingd=4 as an example.With the increase in laser powerp, periodic defocusing oscillation, constant propagation,periodic focusing oscillation,dark solitary waves and catastrophic focusing are illustrated in figure 3(d).For a fixedd,it can seen that figure 3(b) displays a string of dark solitary waves instead of a single one,which is related to the instability of the saddle point in the nonlinear system.
Let us first observe and analyze the parameter regions for a givendin figure 2.It can be seen that there exists a phase transition pointmarked with a rectangle for a givend.Whenr0/rchis larger than the horizontal ordinate of this point, there are five regions which correspond to periodic defocusing oscillation, constant propagation, periodic focusing oscillation, a dark solitary wave and catastrophic focusing, respectively.Whenhowever,there are only three regions for periodic defocusing oscillation,a bright solitary wave and catastrophic focusing,respectively.That is to say, the motions of constant propagation and periodic focusing oscillation are impossible when the injected spot radius is less than a small value.We should emphasize that this finding was omitted and has not been considered in previous work,even in the parabolic channel.Comparing figure 2 with figure 1 in[38],it is found that the parameter regions are much more complex than in[38]and this is induced by containing the ponderomotive self-channeling.Besides solitary waves, we think that the main contribution of ponderomotive self-channeling is catastrophic focusing because it occupies a large area which dramatically decreases the region for stable propagation.
Now, we attend to the influence ofdon parameter areas in figure 2.Obviously, the phase transition point moves towards largerr0/rchwhendincreases.Increasingdflattens the central channel part, which decreases preformed channel focusing whenr0/rchis small.To recover from the loss of the channel focusing effect, a relatively largerr0/rchis naturally needed for the new phase transition point with largerd.For constant propagation,there exists a critical valuer0/rch|1(labeled in figure 2).Whenr0/rch
Besidesd, it can be found from equations (16)–(25) that the parameter regions also depend ona0.In figure 4, we plot the parameter regions for different values ofa0.It can be seen that with increase ina0the phase transition point moves to the bottom right, causing an obvious change in the phase diagram.Correspondingly, the curve of the solitary wave (containing bright and dark solitary waves) moves down,increasing the area of catastrophic focusing; the area of periodic oscillation (containing periodic defocusing oscillation and periodic focusing oscillation) gradually decreases.Meanwhile, the constant propagation curve moves up, inducing an increase in the area of periodic defocusing oscillation and a decrease in the area of periodic focusing oscillation.Compared with the dark solitary wave curve,a0has a more obvious effect on the curves for constant propagation and the bright solitary wave.Now we analyze the reason for the main variations of the parameter regions.According to equation (12), whena0increases and other parameters are fixed, the ponderomotive self-channeling effect is enhanced while the preformed channel focusing effect is weakened.The variation of parameter regions witha0is the result of competition between these two effects.For the parameters around the constant propagation curve,rsvaries about 1.In this case,the reduction of the preformed channel focusing effect induced bya0is more obvious than the enhancement of the ponderomotive self-channeling effect.This causes the constant propagation curve to move up.For the values around the minimumrsof a dark solitary wave, however, the enhancement of the ponderomotive self-channeling effect is relatively obvious this time, and the dark solitary curve moves down.
In figures 2 and 4, the laser propagation behaviors are analyzed in the phase diagram(p,r0/rch),wherepandr0/rchare dimensionless parameters and their variation may mean a complete change of the laser beam and plasma background.Now we study the propagation behaviors from another perspective, i.e.paying attention to the laser behaviors in the parameter space(a0,r0)of the initial laser under the condition of a given plasma backgroundn0andrch.In order to display this simply,we actually use(a0,r0/rch)in the following part.Therefore, by usingn0=0.02ncandrch=30 μm, a corresponding phase diagram is drawn in figure 5(a).As expected,the parameter space is divided into five regions through a phase transition point,and the distribution of these parameter regions is also similar to figure 2 from a topological point of view.However, figure 5(a) reveals some important information that cannot be found from figure 2.Firstly, one cannot simply think that constant propagation can be achieved at any the initial spot radiusr0for a given plasma background.Actually, figure 5(a) only shows a small allowed range, i.e.r0/rch∊(0.24, 0.38).It is worth noting that this conclusion does not mean that the range(0,1)for constant propagation in figure 2 is irrational, because it is always possible to move and adjust the range ofr0/rchfor constant propagation by changing the plasma background.Secondly, on the curve for constant propagation,a0increases rapidly with the decrease ofr0, In other words,a0is sensitive to changes inr0for constant propagation, especially for smalla0.Finally, the above two limitations of the constant propagation condition reveal the importance of focusing and defocusing oscillations.Figure 5(a)shows that there is a considerable area supporting the two behaviors.Figures 5(b)and(c)show the variations of parameter regions with the changes ofn0andrch, respectively.Asn0andrchincrease separately, parameter regions move to the bottom left.Meanwhile,we note that the changes do not induce variation of the main characteristics revealed by figure 5(a).

Figure 5.(a) Parameter regions of laser propagation types in the space(a0,r0/rch)for rch=30 μm and n0=0.02nc.The black,green and red curves represent the conditions for constant propagation,bright solitary wave and dark solitary wave, respectively.The areas beneath the green and black curves, between the black and red curves and above the green and red curves correspond to periodic defocusing oscillation,periodic focusing oscillation and catastrophic focusing,respectively.(b)The variation of parameter regions with n0 for rch=20 μm.From right to left, the curves correspond to n0=0.02nc, 0.04nc and 0.06nc, respectively.(c) The variation of parameter regions with r0/rch for n0=0.02nc.From right to left,the curves correspond to rch=20 μm, 30 μm and 40 μm, respectively.Here, d=4 and nc ≈9.84×1026 m−3 for a laser with wavelength λ=1064 nm.

Figure 6.The modulus of the slowly varying laser envelope |a(r, z)| obtained by numerical simulations with parameters marked by empty circles in figure 2 for d=4, a0=0.3 and r0/rch=0.4.From (a) to (e), p=0.10, 0.23, 0.29, 0.40, 0.58 and 0.59, respectively.
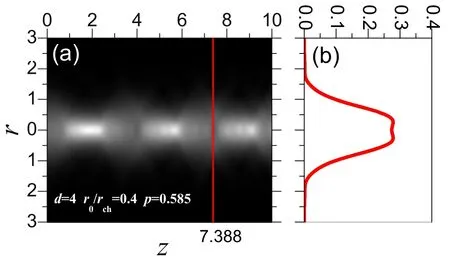
Figure 7.Image profile of |a(r, z)| obtained by the numerical simulation with laser power p=0.585, d=4 and r0/rch=0.4 around the unstable critical value for laser propagation failure.Part(a)presents the image profile and part(b)presents the corresponding modulus of the laser amplitude along the radial direction at z=7.388.
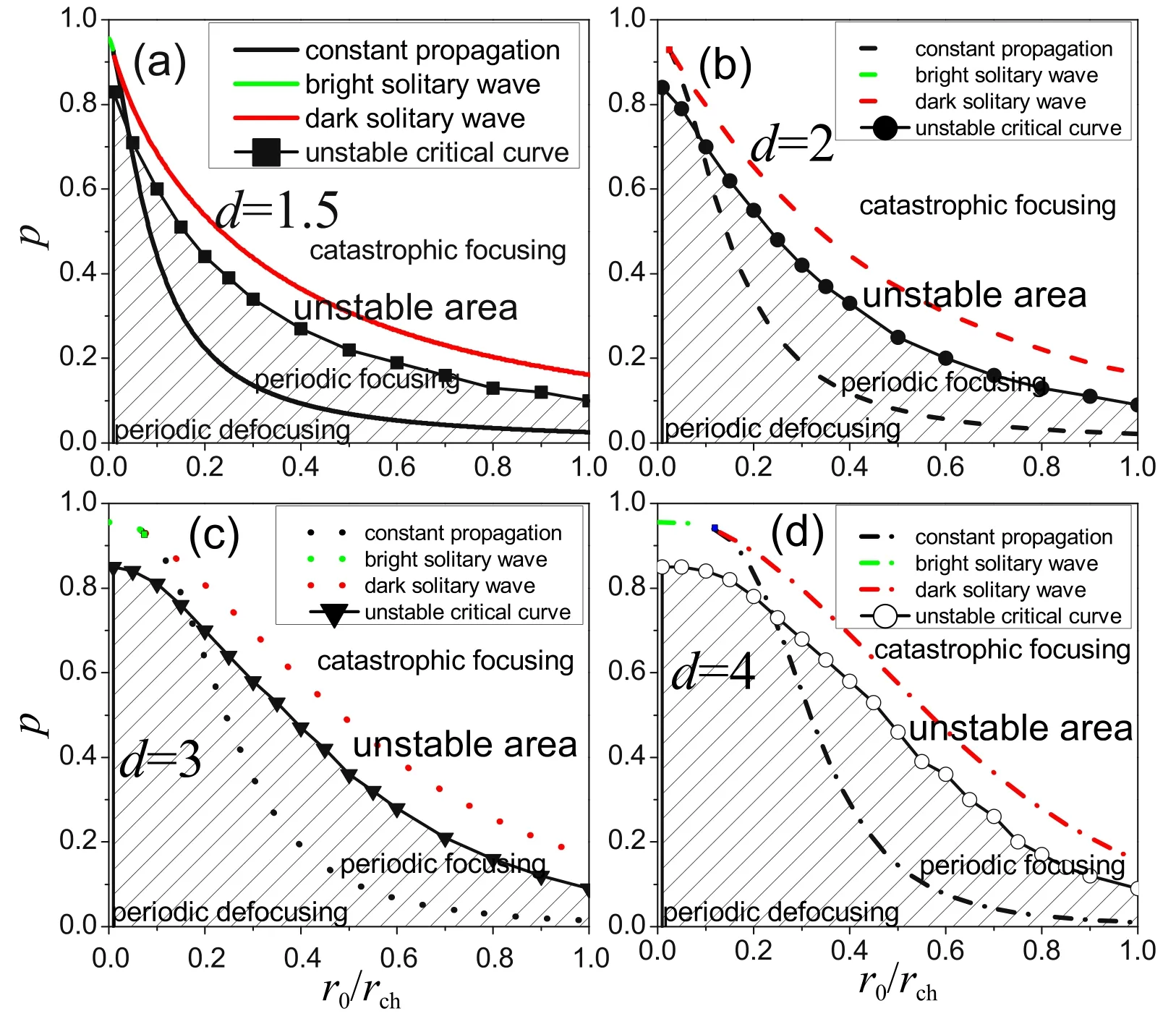
Figure 8.Parameter regions of laser propagation types(shown in figure 2)with unstable critical curves obtained by numerical simulation for d=1.5 in (a), 2 in (b), 3 in (c) and 4 in (d).The curves with black rectangles, black circles, black triangles and white circles represent the unstable critical curves corresponding to different values of d.In the area above an unstable critical curve,the laser beam fails to propagate.Other curves and labels are identical to figure 2.Here, a0=0.3.

Figure 9.The modulus of the slowly varying laser envelope|a(r,z)|obtained by numerical simulation with parameters marked by the empty circle in figure 4 for d=4, r0/rch=0.4 and p=0.29.From (a) to (d) a0=0.2, 0.3, 0.4 and 0.5, respectively.

Figure 10.Sketch map for the properties of the Sagdeev potential.
Considering the complexity of the real propagation and the obvious effects of the channel power-law exponentdand the initial laser amplitudea0, it is necessary to make a numerical simulation of equation (6) to verify the theoretical results in the next section.We will see that the numerical results reveal a new unstable critical curve corresponding to radial instability [49, 50] in parameter space (p,r0/rch).The theoretical predictions below this curve are verified,while the formation of solitary waves is prevented because of the radial instability.Many other interesting findings will be found in the next simulation.
4.Numerical simulation
To illustrate the propagation characteristics of the laser beam and verify the above theoretical results,we will make a direct numerical simulation of the wave equation, i.e.partial differential equation (6), in this section.Therefore, with the assumption of an initial linear dispersion relationwe can simplify equation (6) under axisymmetric condition and normalize it as
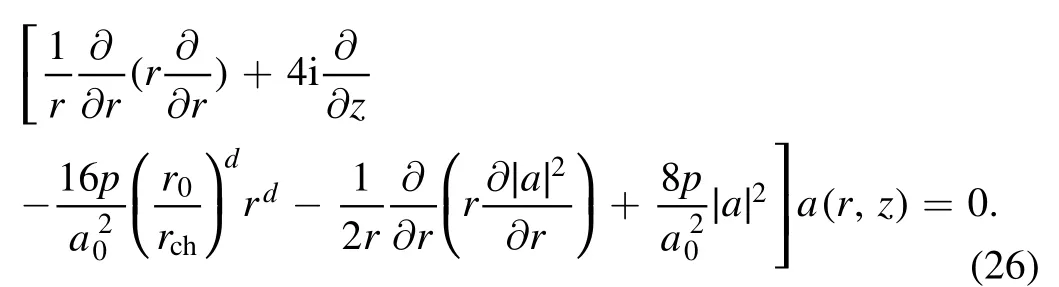
In this equation,ris normalized byr0andpandzare normalized quantities identical to those in equation (12).The injected initial laser beam is set to bea(r, 0) =a0exp( −r2).Then equation (26) can be numerically solved using the finite difference method as successfully performed in[28, 37, 38, 51].
To begin with we make the simulation with parameters marked by empty circles in figure 2 ford=4.The results are presented in figure 6 and the corresponding physical parameters are also labeled.It can be seen that the the simulation results shown in figures 6(a)–(e), corresponding top=0.1–0.58, are identical to the theoretical results shown in figure 2, i.e.figures 6(a) and (b) show periodic defocusing oscillations, figure 6(c) shows constant propagation and figures 6(d) and (e) show periodic focusing oscillations.The measured periods of 4.5 in figure 6(a), 3.3 in figure 6(b), 3.2 in figure 6(d) and 3.4 in figure 6(e) are also approximately equal to the calculated values of the theoretical period formulas given by equations (18) and (20) as 4.2, 3.4, 3.0 and 2.8, where the difference may be relatively large for figure 6(e); we think this is because the corresponding laser power of 0.58 is much nearer the 0.585 of the following radial instability.This good consistency confirms the theoretical results in section 3 and the numerical simulation.However,when the laser powerpexceeds 0.58 and increases to 0.59,the laser beam fails to propagate.Here, we think the appearance of the irregular behaviors (except constant propagation, periodic focusing and defocusing oscillations)means a failure of propagation.With a clear observation of the simulation atp=0.585 shown in figure 7, we find the failure of propagation is related to instability in the radial direction [49, 50] (radial shape change and some microstructures related to the instability can be seen in figure 7(b)).
Numerical simulations with other values ofr0/rchconfirm this phenomenon.That is,for a fixedd,there should exist an unstable critical curve in figure 2, above which the laser beam fails to propagate stably.Ford=1.5, 2, 3 and 4, we plot these unstable critical curves plus the corresponding parameter regions of figure 2 in figures 8(a)–(d),respectively.The critical curves of instability are obtained through a large number of numerical simulations.The discrete values ofr0/rchare 0.01,0.05,0.10,0.15,...,and 1.0 respectively.For a fixedr0/rch,we find the criticalpof failure propagation by changingpin steps of 0.005.The critical curves are obtained by connecting the different critical points.Three important findings can be observed from figure 8.(1)The region above the unstable critical curve covers that of catastrophic focusing and shrinks the region for stable laser propagation further;and because of this, the behaviors of bright and dark solitary waves will never occur and the laser beam can only show periodic defocusing oscillation, propagation with a constant spot radius or periodic focusing oscillation.(2)Whenr0/rchis less than a certain value(the intersection point of the unstable critical curve and the curve of constant propagation) for a fixedd, even the usual constant propagation and periodic focusing oscillation cannot exist and the laser beam can only show periodic defocusing oscillation;in other words,and it is only above this lowest value forr0/rchthat the laser beam can propagate with constant spot radius.(3) With the increase ofd, the lowestr0/rchincreases apparently, and the unstable region above the unstable critical curve shrinks significantly,which enlarges the area for stable propagation.
In the previous theoretical part it was revealed thata0has an obvious influence on the laser propagation parameter region.In order to further verify and visually show the influence ofa0on laser propagation, we make numerical simulations withr0/rch=0.4 andp=0.29, marked with the empty circle in figure 4 for differenta0, and show the results in figure 9.We can see that whena0=0.2, the propagation behavior of the laser is periodic focusing oscillation.Whena0=0.3, the laser propagates with a constant spot radius.Whena0=0.4 and 0.5, propagation takes the form of periodic defocusing oscillations.This is exactly consistent with the theoretical prediction in figure 4.In section 3, figure 5(a)revealed that constant propagation occurs only in a narrow ranger0/rch∊(0.24, 0.38) for the given plasma backgroundrch=30 μm andn0=0.02nc.To verify this result, numerical simulation was performed for some parameter points along two linesr0/rch=0.23 andr0/rch=0.4 on the two sides of the range (0.24,0.38) and also for some parameters of the constant propagation shown in figure 5(a).Atr0/rch=0.23,a0is increased from 0.05 to 0.50 in steps of 0.05.The simulation shows periodic defocusing oscillations.Atr0/rch=0.4,a0is increased from 0.03 to 0.30 in steps of 0.03.The numerical simulation gives periodic focusing oscillations.Constant propagation is also observed for the selected parameter points (r0/rch=0.36,a0=0.23), (0.37,0.16)and(0.38,0.06)on the constant propagation curve.The numerical simulation results confirm the theoretical results in figure 5(a).Due space limitations,the results of the numerical simulation are not presented in this paper.
According to the above analysis,the numerical simulation successfully verifies the theoretical results and finds an unstable critical curve above which the laser beam fails to propagate stably.The unstable critical curve amends the parameter space for laser propagation and gives rise to some interesting results even for the parabolic channel.The modified parameter space varies significantly with the channel power-law exponentd.
5.Summary
Containing the effect of ponderomotive self-channeling, the propagation theory of a laser beam traveling in a power-law channel is developed.Ponderomotive self-channeling induces a large variation of the parameter space(p,r0/rch),which means a much more complex laser behavior.In the variation, more attention should be paid to catastrophic focusing because it occupies a relatively large region and shrinks the domain of laser stable propagation in the parameter space.Increasing the power-law exponent can decrease the catastrophic region,which is beneficial for laser propagation.Increasing the initial laser amplitude, however, may enlarge the catastrophic region moderately and induce obvious variations in the parameter regions for other stable propagation behaviors.The effects of the initial amplitude on the propagation behavior are also presented and studied in another parameter space(a0,r0/rch)for a given plasma background.By directly solving the wave equation with the finite difference method, the propagation dynamics and stability are also studied numerically.The numerical simulation confirms the main theoretical results containing the constant propagation, periodic focusing and defocusing oscillation.Meanwhile,the numerical simulation reveals a radial unstable critical curve in the parameter space(p,r0/rch), above which stable propagation fails.The unstable critical curve brings some interesting findings, for example,it prevents the formation of bright and dark solitary waves and the unstable region above the unstable critical curve covers that of catastrophic focusing and further shrinks the stable domain for the laser beam; this indicates that the laser beam can propagate with constant spot radius only above a certain low value ofr0/rch.The unstable critical curve is sensitive to the channel power-law exponent and this results in the apparent decrease of the unstable region above the unstable critical curve and the increase in the lowestr0/rchvalue for constant propagation with this exponent.It can be seen that the radial instability corresponding to the unstable critical curve is one of the important discoveries in our work, and a detailed theoretical and numerical investigation is necessary.However, this is a systematic work with many calculations and much analysis,and we will address it further in the near future.To summarize,the obtained results recover our previous knowledge and reveal some valuable information about conditions for stable laser propagation, it may therefore help bring insight into the future studies related to laser propagation.
Acknowledgments
This work is supported by National Natural Science Foundation of China (Nos.11 765 017, 11 865 014, 12 047 574,11 847 304,11 764 039 and 12 165 018), and by the Scientific Research Project of Gansu Higher Education(No.2019B-034).
Appendix: properties of the Sagdeev potential
Under the appropriate condition 0
(1) The properties of the roots ofV(rs)=0.Firstly,rs=1 is one of the roots.Secondly, we rewriteV(rs)=0 in the formthen set the expression on the left-hand side asf(rs) and that on the righthand side asg(rs).Obviously, the curvedecreases first and reaches a minimum value then increases finally whenrsvaries from 0 to infinity (this is directly concluded by analyzing the expression).Meanwhile, the curvedecreases quickly, then slowly and finally varies linearly.These are the geometric properties of the two curves.For illustration, an example is shown in figure 10(a).Considering the geometric properties and the asymptotic behaviors∣′f(rs)∣ < ∣g′(rs)∣forrs→0 andf′(rs)>g′(rs)forrs→∞; making an elementary geometric analysis,one can find that there are at most three intersection points between the two curvesf(rs) andg(rs) in the range ofrs>0.This means thatV(rs)=0 has three positive roots at most.In summary, one root ofV(rs)=0 is equal to 1, and there are at most two other positive roots.
(2) The properties of the roots ofV′ (rs)=0.Differentiating equation (14) once, one obtains(1−p) rs2.Considering the conditions 0
 Plasma Science and Technology2021年12期
Plasma Science and Technology2021年12期
- Plasma Science and Technology的其它文章
- Numerical simulation of nanosecond laser ablation and plasma characteristics considering a real gas equation of state
- Effect of edge magnetic island on carbon screening in the J-TEXT tokamak
- Relativistic effect on synergy of electron cyclotron and lower hybrid waves on EAST
- Influence of the X-point location on edge plasma transport in the J-TEXT tokamak with a high-field-side single-null divertor
- A simulation study of protons heated by left/right-handed Alfvén waves generated by electromagnetic proton–proton instability
- Investigation of optimum discharge characteristics and chemical activity of AC driven air plasma jet and its anticancer effect
