台后填土及桥头跳车动力荷载作用下的扶壁式桥台计算分析

李克磊

（宁夏公路勘察设计院有限责任公司，宁夏 银川 750001）

1 引言

公路桥梁桥台形式一般多采用柱式台、肋板台、薄壁台等，在台后填土较高且条件受限无法设置桥台溜坡的情况下，则需采用扶壁台或U型台。扶壁台作为一种轻型桥台，相比重力式U型台，有着结构轻巧、造型美观等优点。但在计算分析扶壁台时，由于台身、扶壁、承台和桩基作为一个整体参与受力，使用常规简化计算方法一般很难得到准确结果[1，2]。

桥头跳车是公路运营过程中的常见问题，是由于路基、桥梁沉降不均而引起的在路桥衔接处发生的车轮震动现象。桥头跳车不仅会影响车辆运行舒适性，降低道路服务水平，而且会增加油耗，加重桥面破损，严重时甚至会导致事故发生[3，4]。

因此，很有必要将桥头跳车动力荷载的作用考虑在扶壁式桥台计算分析当中。以往计算研究多采用有限元软件建立单独桥台模型，台后填土通过手算土压力施加在桥台上，不考虑地基土和桩基础的模拟[5，6]。本文将以一座实际桥梁为例，通过应用有限元软件MIDAS/GTS建立桥台、地基土及台后填土实体模型分别进行有、无桥头跳车动力荷载作用下的受力分析，可根据桥台关键部位的受力情况，指导结构配筋设计。

2 工程概况

某高速公路跨越一座大型灌溉渠及伴渠路，采用3×30m装配式预应力混凝土箱梁结构。桥梁第一孔跨越伴渠路，第三孔除跨越渠道外还需同时跨越渠边砂砾路，末号桥台无法设置台前溜坡，故采用扶壁式桥台，桥型布置如图1所示。

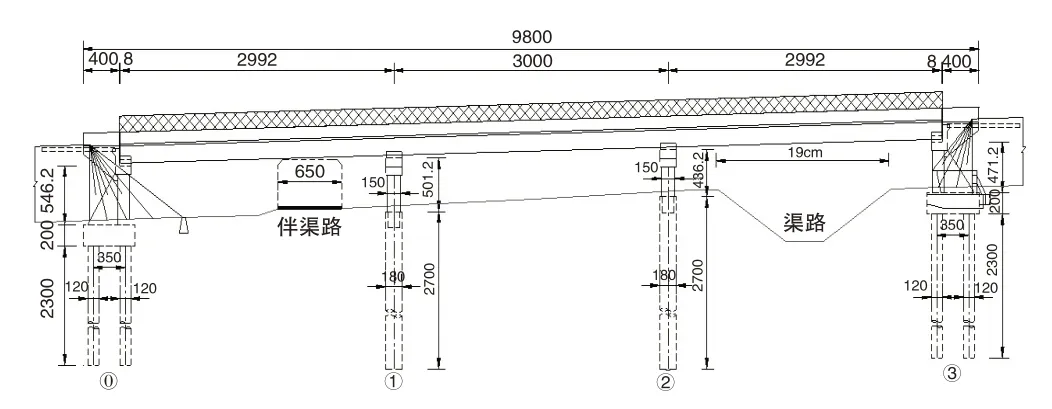
图1 桥型布置图（cm）

本桥末号台半幅桥台宽13.49m，台身净高4.0m。扶壁是桥台重要受力构件，其间距一般为1/4～1/2台身总高，扶壁厚度一般为50cm～80cm，顶底宽度根据台帽、承台尺寸而确定[7]。本桥台共设4道扶壁，扶壁厚0.6m，顶宽0.3m，底宽3.3m；承台厚2.0m，下接6根直径1.2m钻孔灌注桩。桥台除承台桩基采用C30混凝土外，其余部分采用C35混凝土。桥台立面及侧面图如图2、图3所示。

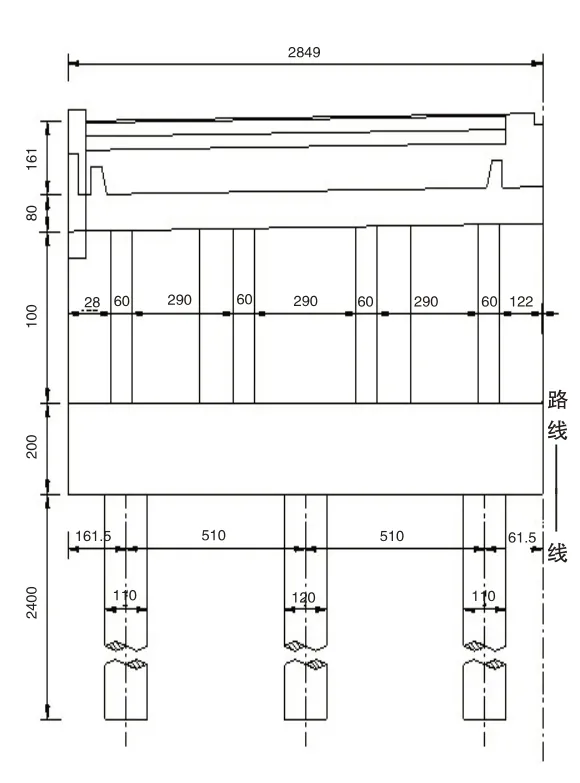
图2 桥台立面图（cm）

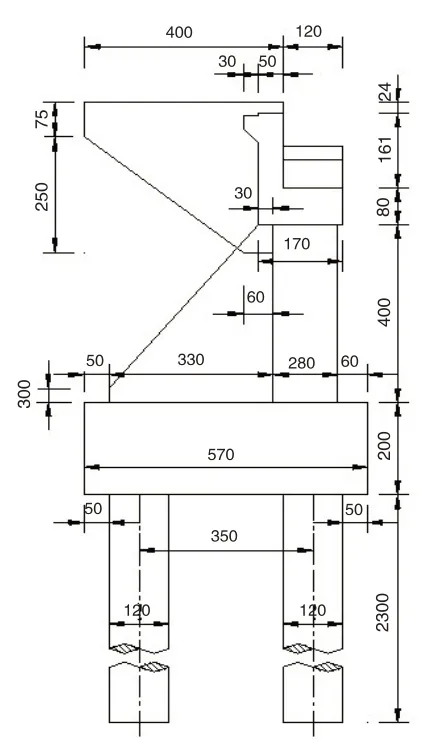
图3 桥台侧面图（cm）

3 模型建立

通过有限元软件MIDAS/GTS建立末号台半幅桥台、地基土及台后填土三维有限元模型，桥台和土体采用六面体单元，桩基础采用梁单元，结构与土体之间采用接触单元模拟二者之间的界面行为，地基土细砂、泥岩和泥质砂岩共三层及台后填土均采用摩尔-库伦模型进行模拟。另外，在承台上部添加测量板单元，用以计算承台内力。地基土及台后填土参数见表1，模型如图4、图5所示。

表1 土层参数表

图4 扶壁台模型图一

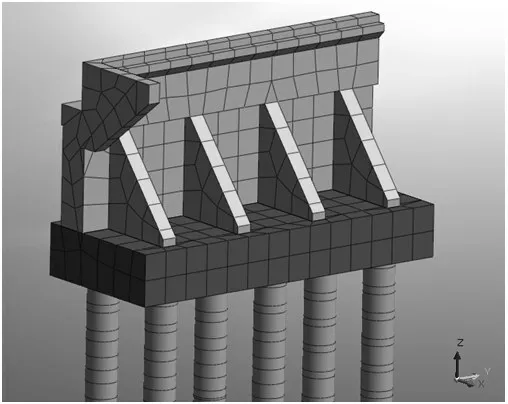
图5 扶壁台模型图二

4 定义施工阶段及荷载取值

根据桥台实际施工步骤，依次建立原场地初始地应力平衡、地基土开挖、结构施工、台背回填、施加上部荷载和车辆运营六个施工阶段。

施加上部荷载为上部结构自重换算为均布压力作用在台帽；车辆运营阶段台后汽车荷载产生的土压力采用车辆荷载换算成等代均布土层厚度，再转化为均布压力作用于台后填土上。而有桥头跳车情况下的台后车辆动力荷载则可根据动力荷载冲击系数得出最大轴重，再将最大轴重换算为等代均布压力作用于台后填土上[8]。

因此，无桥头跳车时，按《公路桥涵设计通用规范》（JTG D60-2015），台后破坏棱体长度l0=5.0m 范围内的等代均布压力为[9]：

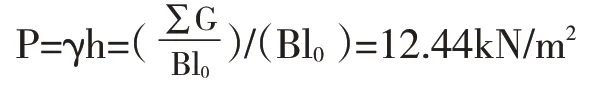
桥头发生跳车时，假定车辆以较低速度30km/h 运行，车辆下桥时前后两个后轴的竖向荷载冲击系数与跳车高度关系见表2[10]。

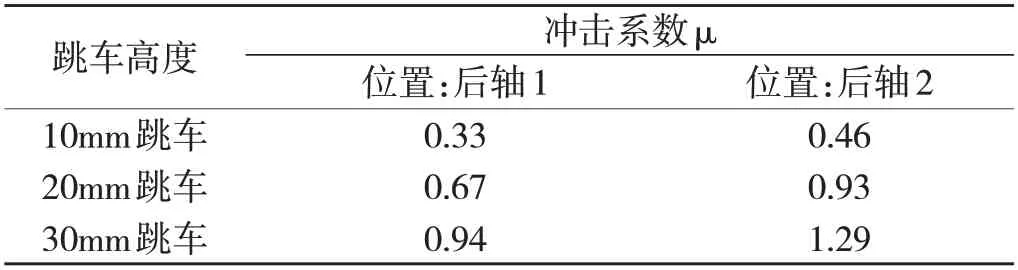
表2 车轮竖向动力荷载冲击系数与跳车高度关系

当速度V=30km/h时，后轴1的最大轮载位置距离错台处约2.0m，后轴2 的最大轮载位置距离错台处约0.4m[10]。综合考虑，有限元建模时可将后轴2的最大轮载等代均布压力作用于0～0.4m 范围，将后轴1 的最大轮载等代均布压力作用于0.4m～2.0m范围，2.0m～5.0m范围仍按无跳车情况考虑。因此，不同跳车高度情况下的台后等代均布压力计算结果见表3。

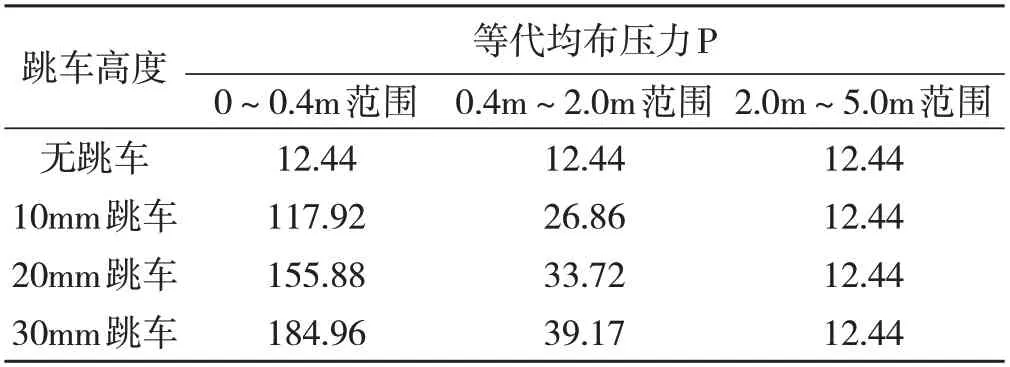
表3 等代均布压力（kN/m3）与跳车高度关系

5 计算结果分析

按照《公路桥涵设计通用规范》（JTG D60-2015），正常使用极限状态设计时汽车荷载不计冲击力，故为了考虑桥头跳车时的动力荷载影响，以下计算均按照承载能力极限状态下基本组合进行。

5.1 桥台应力

运营阶段无跳车时的桥台顺桥向、横桥向应力云图如图6、图7所示。由于台帽、台身、耳墙和扶壁组合为整体结构相互约束并参与受力，有效地使台身应力发生分散，使桥台基本处于受压状态，拉应力不大，最大拉应力出现在台身顶面与耳墙交界位置。桥台在不同跳车高度情况下的最大拉应力计算结果见表4。

图6 无跳车时顺桥向桥台应力云图

图7 无跳车时横桥向桥台应力云图

表4 不同跳车高度情况下桥台应力

由表4可知，随着跳车高度增加，台身、耳墙和扶壁最大拉应力均呈增大趋势，其中顺桥向台身最大拉应力增大相对明显，30mm 跳车高度情况下最大拉应力为1.5MPa，接近C35混凝土轴心抗拉强度设计值1.52MPa。

5.2 承台、桩身内力

根据承台测量板单元和桩身梁单元内力云图，如图8～图11所示，可得出承台最大弯矩和桩身最大轴力、最大弯矩。

图8 无跳车时承台绕横桥向轴弯曲弯矩云图

运营阶段不同跳车高度情况下的承台、桩身内力计算结果见表5。

表5 不同跳车高度情况下承台、桩身内力

由表5可知，随着跳车高度增加，承台、桩身最大弯矩及最大轴力均呈增大趋势，其中承台绕顺桥向弯曲的最大弯矩增大相对明显。

图9 无跳车时承台绕顺桥向轴弯曲弯矩云图

图10 无跳车时桩身轴力云图

图11 无跳车时桩身弯矩云图

5.3 台身、桩顶位移

运营阶段不同跳车高度情况下的台身、桩顶的顺桥向位移计算结果见表6。

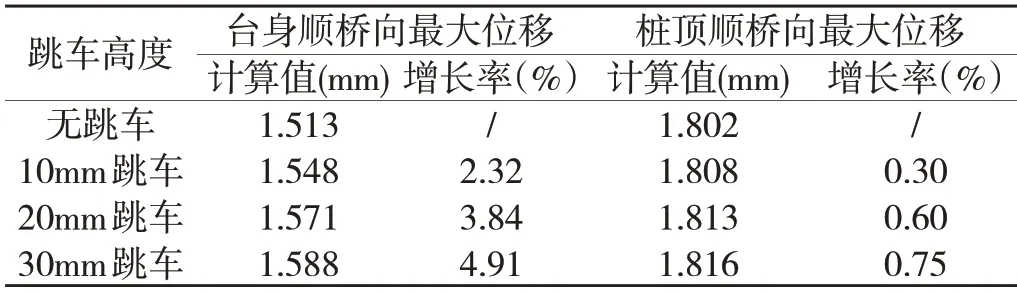
表6 不同跳车高度情况下台身、桩顶位移

由表6可知，随着跳车高度增加，台身、桩顶顺桥向最大位移均呈增大趋势，其中台身位移增大相对明显。

6 结语

通过建立扶壁台、地基土和台后填土有限元模型，根据桥头跳车高度和车轮冲击系数的关系，对不同跳车高度情况下的扶壁台进行计算分析，得出以下结论：

①由于桥头跳车高度增加引起汽车台后等代压力增加，桥台应力，承台、桩身内力和台身、桩顶位移均出现不同程度的增加，其中对台身顺桥向应力、扶壁横桥向应力和承台绕顺桥向弯曲的弯矩影响相对较大，对桩身弯矩和位移影响相对较小。

②通过桥台的应力分布情况，可以确定扶壁台拉应力较大位置即受力薄弱区，比如台身顶面与耳墙交界位置，设计时应针对该位置进行配筋设计，提高桥台结构耐久性。

③桥头跳车作为一种常见现象，在对扶壁台以及承台、桩基进行配筋设计时，应考虑桥头跳车动力荷载影响，保证结构配筋有足够的安全富余度。