基于混合采样的改进随机森林算法研究

王 诚，赵晓培

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

0 引 言

随着网络数据存储和数据收集能力的快速发展，获取海量数据中有价值的信息已经成为人们研究的热点之一，其中分类技术[1]作为数据挖掘[2]中的一大方向，是一种有监督的机器学习方法。它是通过对训练集进行训练得到学习器模型，再用该模型对测试集进行测试得到分类结果。常用的分类器有最小距离法、贝叶斯、决策树、支持向量机[3]、神经网络[4]等，其中的决策树是典型的单分类器，应用较为广泛。但是单分类器存在明显的缺陷，由此组合分类器应运而生，这种多分类器对多个单分类器进行组合、汇总，能够提升分类性能，提高分类器的泛化能力。随机森林算法[5]就是在这种背景下产生的一种多分类器，它是对决策树算法的一种整合。

随机森林(RF)[6]是一种组合分类器，大量的理论和实证研究都证明了随机森林算法具有较高的预测准确率，对异常值和噪声具有很好的容忍度，且不容易出现过拟合。但是，随机森林算法对不平衡数据集的分类效果较差，尤其在疾病检测[7]、故障诊断[8]及信用卡欺诈检测[9]等应用领域，数据集数据分布明显不均衡，其中少数类样本数目过少，导致传统分类器的准确率偏向于多数类，即便准确率很高也无法保证少数类样本均分类正确。

面向不均衡数据分类的研究[10]也成为近年来研究的重点，提出解决不平衡数据[11]的分类策略[12]也层出不穷，总结起来可以归为两方面，一方面是从数据本身出发通过欠采样或过采样的方法，改变数据集中的多数类和少数类数据分布情况以此改变样本数量的分布结构，达到数据的相对平衡，例如HA等[13]提出基于遗传算法的欠采样GAUS算法，通过损失最小化来优化多数类子集以达到数据平衡以及Chawla等[14]提出SMOTE算法，通过过采样在数据中人工合成[15]少数类样本达到数据均衡；另一方面是从算法层面出发包括特征选择和代价敏感等，通过对算法的改进来提高对不均衡数据分类的准确性，例如GUO等[16]提出的特征选择与Adaboost相结合的集成学习算法，通过特征选择提高分类器的分类性能。对于混合采样，郑建华等[17]提出对整个数据集引入过采样因子后随机过采样，之后再随机欠采样对数据均衡。因此，文中从数据层面出发，提出了一种基于混合采样的改进随机森林算法HSRF(hybrid sampling random forest)，针对多数类和少数类进行分别采样。首先通过随机欠采样和SMOTE算法相结合的方式对不平衡数据预处理实现数据均衡，同时引入聚类算法对SMOTE算法进行改进，提升其对少数类样本的采样性能；然后用均衡后的数据训练决策树，同时采用加权投票的方式进一步提高分类性能；最后构造出整个随机森林分类模型。

1 随机森林算法

随机森林算法是由多棵相互独立的决策树分类器集成的大规模、高维度数据学习分类器。它利用bootstrap重抽样方法从原始样本中抽取多个样本，对每个bootstrap样本进行决策树建模，然后将这些决策树组合在一起，通过投票得出最终分类结果。随机森林算法的构建过程如下：

(1)构建多个数据集，在包括k个样本的数据集中，采用有放回的抽样方式选择k个样本，构成中间数据集，然后在这个中间数据集的所有特征中随机选择几个特征，作为最终的数据集；

(2)为每个数据集建立完全分裂的决策树，利用CART为每个数据集建立一个完全分裂、没有经过剪枝的决策树，最终得到多棵CART决策树；

(3)预测新数据，利用随机森林进行预测试时，在解决分类问题方面主要是将k棵决策树的结果采用投票的方式得到，如公式(1)所示。

C(x)=yi,当yi,yj⊂Y且|T(x)=yi|>|T(x)=yj|

(1)

其中，Y为数据类别集合，yi,yj是数据类别集合Y中的任意元素，|T(x)=yi|表示随机森林中对样本x的预测结果为yi的决策树的个数。

2 算法改进

随机森林算法在处理不均衡数据方面分类性能较差，不平衡数据是指类分布明显不均衡的数据，对于不平衡数据的处理，传统平衡化的方法主要是通过欠采样和过采样来进行数据均衡。欠采样是通过减少部分多数类样本数量来降低类间不平衡比例，使数据集趋于平衡。过采样则是增加不平衡数据集中少数类样本的数量，通过合成新的少数类样本来均衡数据。但是，两种采样方法单独使用会存在弊端：一方面，欠采样会导致数据集中的有用信息丢失；另一方面，过采样会增加冗余数据。因此，文中将两种采样方法综合起来，利用各自的优点提出了基于混合采样的改进随机森林算法HSRF。首先，对于不均衡数据集进行预处理，采用随机欠采样处理多数类，同时用改进的SMOTE算法对少数类进行过采样，使数据集达到均衡；然后，用均衡的数据集训练决策树构建随机森林；最后，给决策树赋予不同的权重根据加权投票原则提高模型的分类性能。

2.1 改进的SMOTE算法

SMOTE(synthetic minority oversampling technique)算法是Chawla等提出的处理不平衡数据的算法，该算法通过在数据中增加人工合成的少数类样本使类分布平衡，降低了过拟合的可能性，提高了分类器在测试集上的泛化性能。

SMOTE算法针对少数类数据中的每一个数据样本X，搜索它的最近邻样本K个，再在这些最近邻数据集中随机选择N个样本。则对每一个原始样本数据，选择了K个近邻样本中的N个样本,接下来便是在原始样本数据以及它的近邻样本之间进行插值操作。公式如下:

Xnew=X+rand(0,1)*(Mi-X)

i=1,2,…,N

(2)

其中，Xnew为新插值的样本；X为选择的原始样本数据；rand(0,1)表示0与1之间的某一随机数；Mi为原始样本数据X的最近邻K个样本中选取的N个样本。

但是，SMOTE算法也存在明显的缺陷，该算法在对少数类过采样的过程中不能考虑到边缘数据的分布状态，容易造成边界模糊的问题。因此，文中采用聚类算法对SMOTE算法进行改进，先使用聚类算法对少数类进行聚类操作，根据聚类的区域进行插值增加人造样本数据，这样能很好地解决边界模糊问题。其主要步骤如下：

(1)先用聚类算法对少数类进行聚类操作，获得少数类数据中各簇的分布状态；

(2)计算各个簇的簇心，每一个聚类的簇心为{c1,c2,…,cn}；

(3)在簇内簇心与簇内样本的连线上进行人工样本生成。新插值的公式如下：

Xnew=ci+rand(0,1)*(X-ci)

i=1,2,…,N,X∈ci

(3)

其中，Xnew为新插值的样本；ci为簇心；X是以ci为簇心聚类中的原始样本；rand(0,1)表示0与1之间的某一随机数。

2.2 加权投票原则

对于分类任务来说，随机森林算法采用的是简单投票原则，该原则是将同样的权值赋值到每棵决策树上，忽略了不同分类器之间的强弱差异，无法区分分类性能优秀和分类性能欠佳的分类器，从而导致分类性能优秀的决策树的能力得不到发挥，而分类性能欠佳的决策树对最终分类结果带来一定负面的影响，最终导致分类结果存在偏差。因此，文中采用加权投票的方法增强优秀决策树在投票中所占的比重，同时削弱分类性能欠佳的决策树的比重，以此增加随机森林算法的分类性能。具体步骤如下：

(1)通过Bagging算法从均衡后的数据集N中进行随机抽样，形成样本子集。同时会存在未被抽取的OOB数据，OOB中每个样本没有被抽到的概率约等于0.368，由公式(4)所示。设T为训练完成的决策树分类器集合；

(2)T测试OOB数据，得到每棵决策树对OOB数据的正确分类的比率；

(3)对样本子集使用随机森林进行检测分类并加权统计；

(4)选出得票最多作为最终结果。

2.3 混合采样和随机森林算法结合的HSRF算法

HSRF算法相比于原始随机森林算法有两点改进：第一，针对原始随机森林算法处理不均衡数据准确率低的问题，采用了混合采样对数据集进行预处理，用随机欠采样处理数据集中的多数类，同时用改进后的SMOTE算法处理数据中的少数类，使数据集达到均衡状态；第二，改进随机森林算法中的简单投票原则，采用加权投票原则，给决策树赋予不同的权值，更好地区分分类器的强弱差异。HSRF算法的流程如图1所示。

图1 HSRF算法流程

3 实 验

3.1 实验环境

实验环境的硬件方面主要采用的配置为：Intel(R) Core(MT) i7-4600U CPU @ 2.10 GHz处理器 、8 G内存、64位Windows 10 企业版操作系统。软件环境为Java环境，使用Weka开放源码包。

3.2 实验数据集

实验用到的5个数据集均来自美国加州大学UCI公开数据集，分别是页面块分类数据集(page)、人工字符数据集(artificial)、鲍鱼数据集(abalone)、皮马印第安人数据集(pima)、卫星数据集(satellite)。这5个数据集都是用于分类问题的不均衡数据集，少数类和多数类之间的不平衡比在0.26左右，表现了数据集中数据极度不平衡，有利于展现出HSRF算法对于不平衡数据的处理性能。具体参数如表1所示。

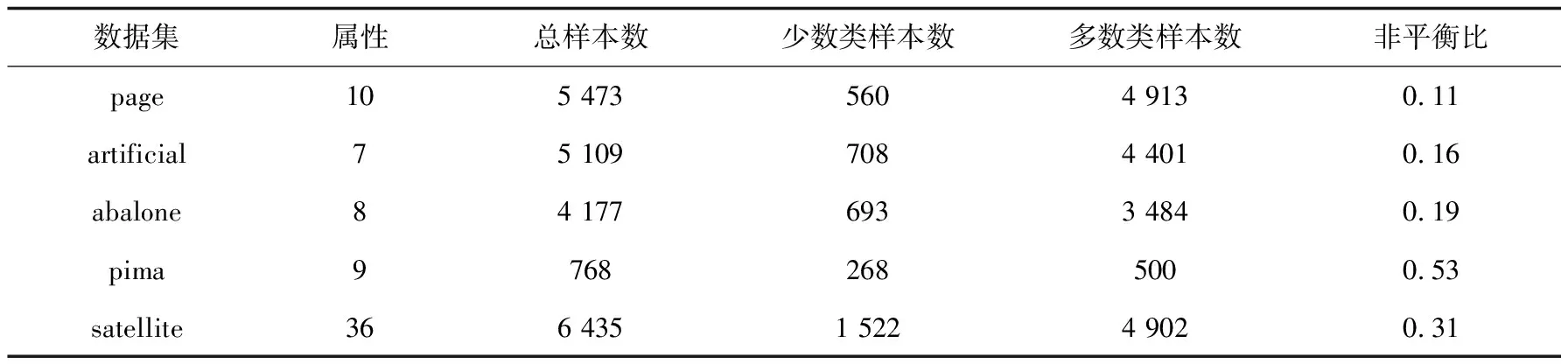
表1 数据集的具体参数

3.3 评价指标

对于传统的分类算法，一般采用分类精度作为评价指标，然而对于不平衡数据集，用分类精度来评价分类器的性能是不准确的。因此对于不平衡数据一般采用G-mean、F-value和ROC曲线(AUC面积)作为评价指标，这些基本上都是建立在混淆矩阵的基础上的。混淆矩阵如表2所示。

表2 混淆矩阵

这个矩阵是定义在验证集上的，表示分类算法可能遇到的情况，其中正类样本和负类样本表示验证集上的真实类标，预测正类和预测负类表示分类算法的预测类标。

(1)几何均值G-mean表示正类分类精度和负类精度的集合平均值，公式如下：

(5)

(2)F-value是一种综合考虑负类查全率和查准率的指标，综合衡量随机森林的分类性能，公式如下：

(6)

其中，precision和recall分别表示查准率和查全率，β的取值范围为(0,1]，通常取1。precision和recall的公式分别如下所示：

(7)

(8)

(3)ROC曲线是不平衡数据分类问题中最经常采用的度量指标，在衡量随机森林在不平衡数据上的整体分类性能，依然可以采用ROC曲线来描述，ROC曲线在坐标轴上越接近左上方则可认为随机森林处理不平衡数据分类问题的效果越好。但是ROC曲线很难直接反映分类器的分类效果，因此，文中采用量化的AUC面积指标来衡量。AUC面积指标指的是ROC曲线之下的面积大小，AUC指标接近于1，则反映出分类器的分类效果越好。

3.4 实验过程

实验将每个数据集按照4∶1的比例随机分为训练集和测试集，用求取平均值的方式来进行结果判定。改进算法的具体实验过程为：首先，针对具体算法对5个数据集的数据进行预处理操作，按照实验要求设定各种参数；然后，在改进的SMOTE算法对于训练集中的少数类处理的时候，将聚类算法的迭代次数的最大值设为50，随机选取5个点作为簇心开始聚类，当迭代达到最大值时，算法结束，记录最终簇心点，接着对该簇心点进行插值操作；最后，根据各个分类器的性能给决策树赋予不同的权值，通过加权投票得出分类结果。

此外，实验通过对比三种不同的分类算法来验证改进算法的分类性能。第一种是原始随机森林算法；第二种是通过SMOTE算法后的随机森林算法SRF；第三种就是文中提出的HSRF算法。

3.5 实验结果分析

实验对比了三种算法分别在5个数据集上各自的评价指标，实验结果如表3所示。

表3 三种算法在5个数据集上的性能指标对比

将RF算法、SRF算法和HSRF算法在5个数据集上的各性能指标绘制成柱状图，如图2～图4所示。

根据图2可以看出，相比于RF算法的G-mean值，SRF算法和HSRF算法在分类结果G-mean值的表现上更好。这五个数据集在不做数据预处理，直接通过RF算法进行分类的情况下，可以看出随着数据集pima、satellite、abalone、artificial的不平衡比逐渐增加，算法的G-mean值越小，最低达到了40.8%，由此看出G-mean值可以很好地反映分类器在不均衡数据集上的分类性能。SRF算法相比于RF算法，通过对少数类的插值来均衡数据，一定程度上提升了算法的分类性能，而HSRF算法对不平衡数据的整体分类性能更高。

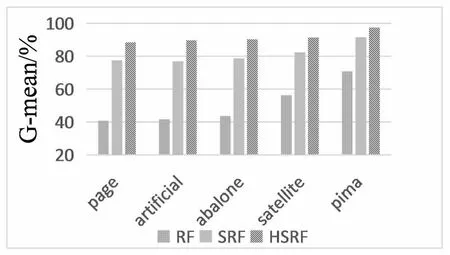
图2 G-mean值比较

根据图3可以看出，随着算法的逐步改进，数据集反映的F-value值在不断地提升，HSRF算法最高可以达到97.1%，有很好的分类效果，而原始随机森林RF算法的F-value值基本都在90%以下，说明原始随机森林RF算法在处理不均衡数据集上的性能较差。

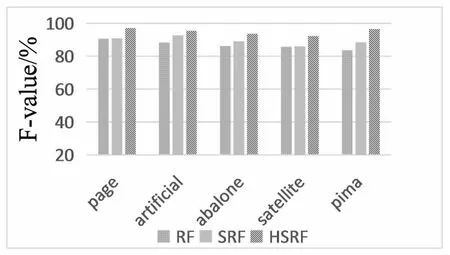
图3 F-value值比较

根据图4的AUC面积指标可以看出，HSRF算法在采用混合采样对数据集均衡化处理之后，AUC指标有较大的提升，数值都远超过了其他两种算法，最高达到98.7%。同时在柱状图的对比中可以看出，在数据非均衡比高的数据集中，改进的幅度不是很大，而在不平衡程度增加的情况下，AUC的数值有明显的提升，说明改进后的算法在处理不平衡数据分类问题上有很好的鲁棒性。

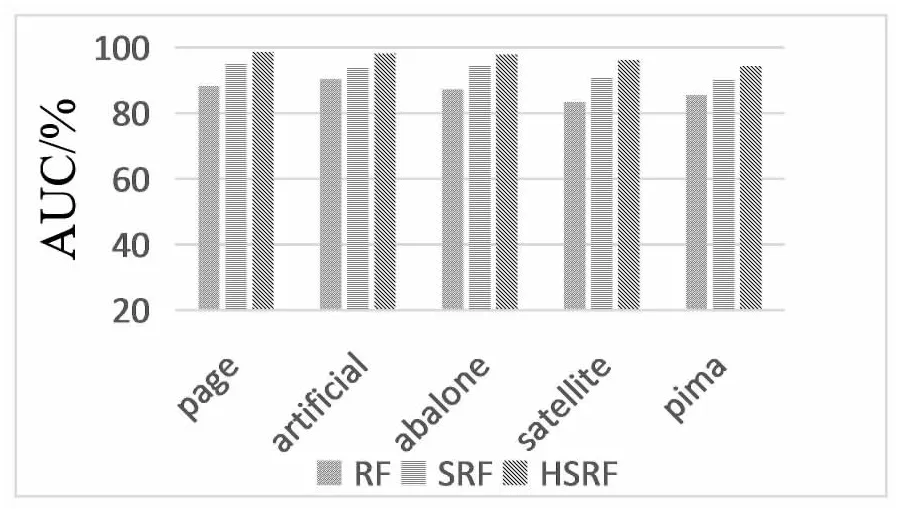
图4 AUC值比较

从图2、图3和图4可以看出，相比于RF算法和SRF算法，HSRF算法在处理不平衡数据上的分类性能更好。综上所述，基于混合采样的改进随机森林算法HSRF与RF算法和SRF算法相比较，不论是在处理不均衡数据的性能上，还是在最终的分类效果上都有明显的提升。

4 结束语

面对不平衡数据的分类问题，基于混合采样对随机森林算法进行了改进，提出了HSRF算法。一方面，该算法针对原始随机森林算法处理不均衡数据准确率低的问题，采用了混合采样对数据集进行预处理，用随机欠采样处理数据集中的多数类，同时用改进后的SMOTE算法处理数据中的少数类，使数据集达到均衡状态；另一方面，算法改进了随机森林算法中的简单投票原则，采用加权投票原则，给决策树赋予不同的权值，更好地区分分类器的强弱差异。结果表明，基于混合采样的改进随机森林算法在处理不均衡数据方面的分类能力比其他分类算法更好。然而HSRF算法也存在一些缺陷，该算法的分类效率较低，所以下一步的研究是在不降低分类性能的前提下提高分类效率。