在不平衡数据中进行高效通信的联邦学习
舒志鸿,沈苏彬
(1.南京邮电大学 计算机学院,江苏 南京 210046;2.南京邮电大学 通信与网络技术国家工程研究中心,江苏 南京 210046)
0 引 言
随着互联网以及移动终端技术的持续发展,智能手机等移动设备已经成为人们生活中不可或缺的组成部分,并在与用户交互的过程中产生了大量的数据。使用机器学习算法对这些数据进行深度分析可以帮助服务商充分了解用户,为用户提供更好的服务。传统的机器学习策略要求移动设备将数据上传到云服务器或数据中心进行处理[1],然而,数据隐私和安全问题越来越受到社会及公众的重视,例如欧盟在2018年推出的《通用数据保护条例》[2]中明确规定数据的收集和存储必须在消费者同意的条件下进行。在这种趋势下,传统方法或将不再适用。
为了解决该问题,Google[3]提出了一种分布式的机器学习方法,称为联邦学习(FL)。在FL中,客户端在本地训练自己的局部模型,然后仅仅将局部模型的参数发送到服务器进行聚合,以更新全局模型。FL重复上述过程直到全局模型收敛或达到所需的训练准确率为止。区别于典型的分布式机器学习,FL的一个关键特征是数据的异质性,即:
(1)非独立同分布(Non-IID):移动设备上的本地数据集取决于用户的使用情况,因此任意客户端的本地数据分布都无法代表全局数据的分布。
(2)不平衡:用户使用服务或应用程序的频率不同,造成客户端上的数据量存在差异。
由于模型参数的庞大以及移动设备有限的通信带宽,通信成本成为制约FL发展的主要因素之一[4]。为了应对这一挑战,McMahan等人[5]提出了目前广为使用的FL算法联邦平均(federated averaging,FedAvg),他们以平均的方式聚合各个参与方的局部模型以更新全局模型,并通过增加聚合期间局部模型的训练次数,减少通信开销。这项研究考虑了客户端上数据量的差异,但却假设全局数据平衡分布,即在所有客户端收集到的数据中各个类别的样本数量分布是均衡的。
然而在许多实际应用中都存在全局数据不平衡的情况,例如欺诈检测[6]、图像识别[7]等。而Duan等人[8]通过进一步的研究表明,FedAvg在全局数据不平衡时的表现不佳。
该文主要研究全局数据不平衡时FL通信效率的优化,在FedAvg的基础上提出了一种基于数据分布加权聚合的FL算法(federated learning with data distribution weighted aggregation,FLDWA)。FLDWA通过客户端的本地数据分布与平衡分布之间的海林格距离衡量本地数据的平衡程度,并将相关信息发送至FL服务器。然后,FL服务器据此为客户端执行加权聚合,从而在全局数据不平衡时更加高效地提取局部模型的信息。
在公开数据集MNIST[9]上使用多种不同的设置进行了仿真实验,以验证所提出方法的正确性和有效性,该数据集已被广泛用于FL的相关研究中。实验结果表明,在不平衡的MNIST上,FLDWA可以有效提升FL的通信效率。
1 相关工作
优化FL在全局数据不平衡时的通信效率,一个直接的想法是解决全局数据不平衡问题。在本节中,从不平衡数据上的机器学习以及联邦学习两个角度介绍和分析相关的一些研究。
(1)不平衡数据上的机器学习。
数据不平衡主要是指数据集中某些类的样本数量远大于另一些类。一般将样本数量非常多的类称为多数类,样本数量较少的则称为少数类[10]。该问题可以通过修改训练数据或调整学习策略加以解决[11]。前者旨在删除部分多数类(欠采样)或生成部分少数类(过采样)样本使数据分布重新达到平衡状态,文献[12]提出了一种基于聚类的欠采样方法,通过K均值聚类算法对多数类进行了聚类,并用聚类中心代替同簇数据。Chawla等人[13]提出了合成少数类过采样技术(SMOTE),通过对少数类进行分析并结合线性插值的方法生成新的少数类样本。调整学习策略的方法则致力于对损失函数进行修改从而削弱算法对少数类的偏见,最受欢迎的方案是代价敏感学习[14]。该方法增加了少数类样本的误分类成本从而提高了对少数类的关注。文献[15]中使用了再缩放技术对代价敏感学习进行改善,使其能够适用于多分类任务。
然而,上述方法不适用于FL。FL数据仅能够被其拥有者所访问,导致采样的方法难以实现。并且由于无从获取整体数据的分布情况,调整学习策略的解决方案仅能在局部使用,这将导致各个用户的局部模型不一致。
(2)联邦学习。
通信效率的优化一直是FL的主要研究方向之一。McMahan等人[16]提出了结构化更新和粗略更新,通过稀疏化和编码技术实现了传输参数的缩小。文献[17]对模型参数进行了有损压缩,并且通过在训练过程中删除固定数量激活单元的方法进一步简化了参数的复杂度,实现了通信开销的优化,从而扩展了文献[16]中的研究。虽然压缩模型参数的方法拥有极强的泛用性,但会导致准确性的牺牲。
Chen等人[18]将神经网络分为深层和浅层,并以不同的频率更新它们的参数,同时根据参数的时效性调整了聚合策略,实现了通信成本的降低。Liu等人[19]设计了一种具有客户端-边缘-云的分层FL系统,通过各层之间的协作减少了资源的消耗。Yao等人[20]将最大均值差异(MMD)引入损失函数中,通过最小化局部模型和全局模型的MMD损失,减少了算法所需的通信回合。然而,上述工作没有考虑到全局数据不平衡对FL的影响。
目前只有少数研究关注全局数据不平衡问题。Duan等人[8]通过数据扩充减轻单个客户端的不平衡程度,并且在服务器与客户端之间设置中介,根据客户端数据分布的Kullback-Leibler距离重新安排它们的协作训练。该方法引入了不可忽视的存储和时间开销,这可能会成为应用的限制。
与上述的研究相比,笔者更加关注方法的普适性,致力于在尽量避免额外的成本或牺牲的情况下,提升全局数据不平衡时FL的通信效率。
2 传统联邦学习方法
通常,FL包含两个主要的实体,即客户端和服务器。客户端k(k=1,2,…,K)持有一个私有的本地数据集Dk,并在Dk上最小化损失函数fk(w)以训练局部模型。令D=∪k∈KDk表示全局数据集,|D|和|Dk|分别表示全局数据集以及客户端k上的本地数据集的数据量。则FL的优化目标定义为:
(1)
其中,F(w)为全局模型的损失函数,定义如下:
(2)
在FL中,服务器收集所有局部模型的模型参数,并通过将它们聚合以更新全局模型。所以,FL的性能在很大程度上取决于聚合策略。目前广泛使用的聚合策略是由FedAvg算法[5]中提出的平均聚合,其具体实现由式(3)给出:
(3)

3 数据分布加权聚合的联邦学习方法
在对不平衡数据集进行分类操作时,算法为了提高分类精度,会倾向于将多数类分类正确,从而对少数类产生偏见。所以对于同一个机器学习任务,通常使用分布更加平衡的训练数据得到的模型质量也会更高。
由于数据隔离的原因,FL无法直接使用全局数据进行训练,而是通过聚合局部模型达到学习的目的。当全局数据不平衡时,由于FL的本地数据集具有非独立同分布的特点,各个客户端的本地数据在分布平衡程度上出现差异,导致训练出来的局部模型质量也会有所差异。由式(3)可知,FedAvg算法中的聚合策略仅根据客户端上的数据量确定相应局部模型的权重。这可能并不合理,因为数据分布更为平衡的客户端通常会训练出质量更高的局部模型,应该在聚合时具有更高的权重。
本节提出的数据分布加权聚合的联邦学习(FLDWA)方法在FedAvg的基础上加入了对数据分布的考虑。量化了每个FL本地数据集的平衡程度,据此调整了聚合策略,从而更加有效地提取局部模型的信息。此外,只要本地数据集不发生变化,其平衡程度也不会改变。所以在算法的执行过程中,客户端只需首次与服务器通信时将相关信息上传即可。
(1)本地数据集平衡程度的量化。
使用海林格距离对本地数据集的平衡程度进行量化。在概率论和统计理论中,海林格距离被用来度量两个概率分布的相似程度[21]。设两个离散概率分布分别为U=(u1,u2,…,un)和V=(v1,v2,…,vn),则它们之间的海林格距离定义为:
(4)
于是,本地数据集的平衡程度可以通过计算其与平衡数据集的海林格距离来刻画。平衡数据集是指各类别样本数量分布均衡的数据集,但目前还没有研究指出各类别样本需要满足何种数量关系才能定义为均衡,该文不解决此问题。由此,定义了一个基准数据集Db作为平衡数据集的替代。在基准数据集中,各个类别的样本数量严格遵循1∶1∶…∶1的规律。
本地数据集与基准数据集的海林格距离越小,表示两者的相似度越高,也即该数据集的平衡程度越高。值得注意的是,海林格距离与相似度是负相关的,为了便于后续的计算以及更为直观地表示平衡程度,需要对其进行转换。考虑到海林格距离满足柯西-施瓦兹不等式,所以其具有如下性质:
0≤H(U,V)≤1
(5)
最终,使用式(6)所示的Bk表征本地数据集Dk的平衡情况,称为平衡度。它是通过将式(7)计算出的本地数据集与基准数据集之间的海林格距离关于其值域进行翻转后得到的:
Bk=1-Hk
(6)
Hk=H(Pk,Pb)
(7)
其中,Pk和Pb分别为本地数据集Dk与基准数据集Db上的概率分布。
(2)局部模型的聚合策略。
在FedAvg中,聚合策略仅根据客户端的数据量进行加权,其权重为:
(8)
在此基础上加入了对客户端上本地数据分布的考虑。为此,将上节中得到的平衡度通过归一化的方法转化为权重的形式。具体计算方式为:
(9)
FLDWA通过结合上述两种权重得到最终的综合权重。考虑到随着实际情况的变化,两种权重会对综合权重产生不同的影响,所以定义了影响因子eq和es表示它们对综合权重的影响程度。虽然数据量和平衡度都会对局部模型的质量产生作用,但是权重计算的是客户端在某个因素上的相对差距。例如数据量相同的多个客户端,通过式(8)计算出的权重也是相同的,此时可以仅使用由式(9)所确定的平衡度权重进行加权,因为数据量对局部模型质量的影响不存在差异。

(10)
(11)
基于此,将式(3)的聚合策略改写为:
(12)


4 仿真实验
文中实验是在MNIST数据集上进行的。该数据集共包含60 000张训练图像和10 000张测试图像。测试图像中,不同类别对应的图像数量在892到1 135之间,为了构造出分布平衡的测试集,随机删除了一些图像,最后使所有类别对应的图像数量都为892张。
采用多层感知机(multilayer perceptron,MLP)和卷积神经网络(convolutional neural networks,CNN)两种模型来评估文中的研究,其网络结构与文献[5]中使用的模型保持一致。同时,选择FedAvg作为基准算法进行对比,该算法目前已用于众多FL实际应用中[22]。
为了对FLDWA进行测试和评估,设计了两组实验。第一组实验探究了本地数据集的平衡程度对算法的影响,第二组实验则对比了FLDWA与基准算法在多种不同设置下的表现。实验中所有结果皆为10次独立实验的平均值。
(1)本地数据集的平衡程度对算法的影响。
该实验为对照实验,分为正常组和不平衡组。从MNIST中抽取了4个数据量相同的子集作为本地数据集分发给客户端,正常组中4个本地数据集都是平衡数据集,不平衡组中则含有一个极度不平衡的本地数据集,其仅持有一个类别的数据样本。
图1显示了FLDWA和基准算法在正常组和不平衡组使用CNN模型达到98%准确率所需的通信回合。可以看出,正常组中FLDWA与FedAvg的性能相同,因为相同的客户端数据分布并未对算法产生影响,此时可以将FedAvg视为FLDWA的一种特例。在不平衡组中,两种算法所需的通信回合都出现了增长,但FedAvg需要额外30%的回合才能达到目标准确率。这表明使用平衡度低的本地数据集训练的局部模型质量较低,由于FedAvg在聚合时对所有局部模型一视同仁,因此其性能明显低于FLDWA。

图1 两种算法达到目标准确率所需通信回合对比
图2显示了FLDWA中的聚合权重。FLDWA为数据不平衡的客户端4分配了很小的权重,限制了其在聚合时的影响力,其他平衡的客户端被分配以较高的权重。可以发现,FLDWA能够准确识别本地数据集的平衡度为其分配合适的权重,更加有效地聚合各方的信息。

图2 FLDWA中客户端的聚合权重
(2)FLDWA与FedAvg的对比。
在该实验中,分别使用MLP和CNN模型对FLDWA和基准算法进行了对比,并且根据客户端上数据量是否相同,每种模型又分别进行了两组实验。构造客户端数据时,为了反映出FL数据非独立同分布的特点,在保证全局数据不平衡的前提下,随机控制本地数据集中的类别个数以及各个类别样本的数量,并且使得任何本地数据集之间都不存在相同的样本。
图3比较了两种算法在不同设置下的性能表现。可以观察到,FLDWA在各种设置下都以较少的通信回合达到了同样的准确率,并且在相同的通信回合中,其准确率均优于基线算法。这充分证实了FLDWA的聚合策略更为高效,有助于生成性能更好的全局模型。另一方面,(a)(c)两组实验中,客户端的数据量是相同的,此时FLDWA的聚合权重仅与本地数据集的平衡度有关。这也表明根据平衡度进行全局模型的聚合可以取得良好的效果,是一种有效的方法。

图3 不同实验设置下的测试集准确率和通信回合的关系
表1中列出了不同的设置下(对应于图3中的(a),(b),(c),(d))使用两种算法达到目标准确率所需的通信回合(MLP模型目标准确率为93%,CNN模型则是98%),以及FLDWA相较基线算法的通信回合减少率。可以观察到在(a)组实验的设置下,FLDWA达到目标准确率平均需要118轮通信回合,而传统的FedAvg则需要大约143轮才能取得同样的效果,从而降低了17.4%的通信成本。尽管实验设置不尽相同,但在(b),(c),(d)三组实验上均可以得出类似的结论,所提出的算法分别将通信成本降低了15.6%、14.6%和15.8%。这证实了在全局数据不平衡时,FLDWA具有更高的通信效率,并且对于不同的数据量情况和不同的机器学习模型都具有很好的鲁棒性。

表1 不同设置下FedAvg和FLDWA达到目标 准确率所需的通信回合以及以FedAvg 为基准的通信回合的减少率
此外,作为对比和补充,也对FLDWA在全局数据平衡时的表现进行了评估。实验结果在表2中进行了展示。
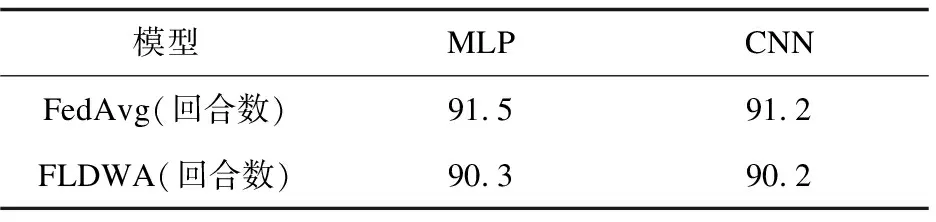
表2 全局数据平衡时FedAvg和FLDWA达到 目标准确率所需的通信回合
从数据中可以看出在全局数据平衡时,两种算法达到目标准确率所需的通信回合差异较小,FLDWA仅带来了微弱的提升。这可能归因于全局数据平衡时,虽然也可能会出现分布不平衡的本地数据集,但是该数据集中缺失或冗余的信息恰好与其他本地数据集对应的部分互补,于是局部模型通过平均聚合能够获得很好的调整。同时这也表明,FLDWA同样适用于全局数据平衡任务,并且在多数情况下表现出优于FedAvg的通信效率。
5 结束语
该文提出了一种基于数据分布加权聚合的FL算法FLDWA,旨在提升FL在全局数据不平衡时的通信效率。该算法基于海林格距离对客户端的本地数据分布平衡程度进行了量化,并据此重新确定了其在FL聚合时的权重,使算法在更少的通信回合内收敛或达到目标准确率。实验结果表明,与流行的FL算法FedAvg相比,该方法有效降低了通信成本,并且在采用不同的机器学习模型和本地数据集大小时都有着很好的表现,具有较强的泛用性。
在接下来的工作中,将对该算法进行扩展,结合同态加密、安全多方计算等技术进一步为FL提供更强大的安全保证。此外,可能存在恶意节点向FL服务器发送错误的模型更新信息,从而降低FL的性能。如何检测和避免恶意攻击也是接下来重点关注的研究方向。

