小型化超材料吸波体设计与电磁吸收分析

雷晓勇 霍树云 李燕 王蒙军，2 孙喆 于河源 李尔平，2，4

（1. 河北工业大学电子信息工程学院，天津 300401；2. 电工装备可靠性与智能化国家重点实验室，天津 300401；3. 中国计量大学信息工程学院 浙江省电磁波信息技术与计量重点实验室，杭州 310018；4. 浙江大学 浙江省先进微纳电子器件智能系统及应用重点实验室，杭州 310027）

引 言

随着电子设备工作频率与集成度的不断提高，电磁干扰问题愈发严重，成为专家和学者研究的重点和难点. 目前，普遍采用两种方案进行辐射抑制：一种是反射型，比如使用溅射和电镀在封装上涂抹小于10 μm 的金属导电层，通过反射防止电磁干扰；另一种属于吸收型，辐射的电磁能量被完全吸收，不会发生能量泄漏，能够更好地保护电子设备[1-3].

传统的吸波体在厚度上无法突破λ/4的限制，使得尺寸偏大，不适用于小型化的电子设备. 2008 年波士顿大学物理系的Landy 等[4]首次提出超材料吸波体，介质材料采用FR4，上层开环谐振器保证电谐振的产生，通过结构的调整使其与介质背板的金属条形成磁谐振保证能量的吸收，在11.5 GHz 产生一个大于88%的吸收峰. 然而，早期提出的超材料吸波体带宽较窄、尺寸较大. 为拓宽带宽，2017 年印度理工学院的A. Bhati 等[5]提出采用介质盖与超材料结合的方法，增加谐振点，从而增加吸收带宽，结构尺寸为10 mm×10 mm×3 mm，但极化敏感性较差. 同年，马来西亚的M.M. Gajibo 等[6]设计一款双波段可切换的超材料吸波体，结构类似于一个横躺的“H”，当入射电磁波角度在0°～60°变化时，吸收率都稳定在90%以上，单元尺寸减小到6.2 mm×4.9 mm. 随着研究的不断深入，2018 年华南理工大学的Huang 等[7]提出一种覆盖X 和Ku 波段的超材料吸波体，通过加载集总电阻的方式实现超带宽，由于中心对称结构使得偏振不敏感，在7.9～20.2 GHz 实现90%以上的吸收率，厚度达到0.093λ . 2019 年M. M. Bait-Suwailam等[8]通过在柔性基底上加载变容二极管实现频率重构特性. 除此之外，还有通过石墨烯、加载电阻膜和多层堆叠的方法实现多频点和超宽带吸收[9-11].2020 年Gaurav Singh 等[12]提出两种宽带吸波体，分别基于电路模拟和电容电路，通过多个电阻层与空气层堆叠实现宽带，空气层的加入必然导致厚度增加、体积变大，不适用于小型化的电子设备中. 因此小型化超宽带极化不敏感的超材料吸波体是目前研究的主要方向.

针对以上问题，本文提出了一种小型化超宽带的超材料吸波体，利用对称弯曲90°的金属结构作为超材料单元. 由于尺寸的限制，通过增加谐振点来取代传统加载集总电阻的方式拓展带宽，结构简单，易于实现. 超材料单元介质板采用传统的FR4，厚度突破传统λ/4的限制，达到0.062 λL. 为防止发生透射，结构背板全覆铜，实现10～18 GHz 的超宽带吸收性能，吸收率达到90%以上. 最后，利用等效电路法提取等效参数，结合理论和仿真推导超材料单元的吸收机理，同时分析了结构参数对吸收率的影响，并通过实验验证其吸收性能.

1 超材料吸波体的设计与分析

1.1 单元结构的设计

超材料吸波体通常是利用周期金属结构印刷在介质板上，并根据实际设计需要调整结构参数实现阻抗匹配，达到高吸收率的目的. 当电磁波垂直入射到金属结构表面，会发生反射或者透射，反射系数和透射系数分别为R(ω)和T(ω). 根据能量守恒定律，除反射和透射外剩余部分能量被超材料吸波体吸收，吸收率A(ω)可表示为

式中：R(ω)=|S11|2；T(ω)=|S21|2. 由于吸波体的背板全覆铜，使得电磁波无法透射，即T(ω)=0，吸收率的表达式简化为

因此，当反射系数接近于0 时可达到最大的吸收效率.

图1(a)为本文所设计的超材料吸波体单元结构的主视图，图1(b)为三维结构图，类似于一个“三明治”，顶层的金属条弯曲90°对称放置，通过增加一组对称弯曲的金属条来增加谐振点，最终实现超宽带.为保证在X 和Ku 波段实现高吸收率，将金属结构印刷在传统的FR4 基板上，材料的介电常数为4.3，损耗角正切为0.02. 并且耐高温，熔点达到203 ℃，在电子设备工作时产生的温度不会影响吸波体的正常工作. 同时，介质底层全覆铜，确保无透射，铜的电导率为5.7×107S/m，厚度均采用0.018 mm. 所有的几何参数如表1 所示.

表1 单元结构几何参数值Tab. 1 Geometric parameters of element structuremm

图1 超材料吸波体模型示意图Fig. 1 Schematic diagram of metamaterial absorber model

1.2 仿真分析

该吸波体单元是在方型开口谐振环的基础上进行改进，使得两组金属条在不同频率下产生共振，得到多个谐振点. 同时，金属条的两个方向增加了缝隙，相当于在45°方向对金属条进行切割，导致更多的电偶极子与磁偶极子产生，使得吸收带宽的范围更大[13].

研究中利用CST 仿真软件进行建模计算，通过频域求解器得到S 参数，X和Y方向的边界条件设置为“unit cell”，Z方向上设置为开放边界. 图2(a)为超材料吸波体在TE 和TM 极化方式下电磁波垂直入射时的S 参数. 由于结构的中心对称特性，明显可以看到两种极化方式的S 参数基本一致，从而验证了其极化不敏感性. 不仅如此，-10 dB 以下带宽覆盖X 和Ku 波段，相对带宽达到57.1%，实现了超宽带.根据式(2)得到虚线所示的吸收率曲线，10～18 GHz频段范围内吸收率达到90%以上，可以高效吸收入射的电磁波.

图2 不同极化方式下超材料吸波体的S 参数与吸收率Fig. 2 S-parameters and absorptivity of metamaterial absorbers under different polarization

为验证结构的角度稳定性，对超材料吸波体结构进行斜入射仿真分析. 图2(b)、(c) 分别展示了TE 和TM 极化方式下吸收率受不同入射角影响的关系曲线，当入射电磁波角度为45°时，无论是TE 还是TM 极化波在16 GHz 的谐振点吸收率均下降，但相对低一点的10.8 GHz 吸收率仍然很高. 并且对该结构来说，入射角度变化对TE 极化波影响较大，随着入射电磁波角度的增加，谐振点均向高频有一定偏移，吸波体的吸收效率在工作频段内始终高于80%，可以预测即使入射角度超过45°，10.8 GHz 附近的一定带宽范围内仍具有较高的吸收率. 因此，超材料吸波体在0°～45°依然保持着高吸收率，即具有良好的角度稳定性.

2 吸波原理分析

2.1 电磁参数提取

为验证超材料吸波体单元的吸收原理，通过软件对10.8 GHz 和16 GHz 两个吸收峰处的表面电流与电场分布进行仿真分析. 图3 中(a)、(b)分别展示的是10.8 GHz 处顶层和底层表面电流分布，(d)、(e)分别展示的是16 GHz 处顶层和底层表面电流分布，可清楚地看到表面电流主要分布在最外侧的对称金属条上. 同时，顶层和底层的电流方向相反构成循环电流回路，激发磁偶极子引起磁共振从而控制磁导率µ(ω)的大小.

图3 表面电流与电场分布图Fig. 3 Distribution of surface current and electric field

图3(c)、(f)分别展示了10.8 GHz 和16 GHz 的电场分布，通过颜色的分布可以看到顶层外侧边缘弯曲的金属条部分感应出很强的电场，从而产生电共振可以有效地控制介电常数ε(ω). 因此，可以通过调节电磁共振实现自由空间阻抗匹配，达到宽频带高吸收率的目的. 同时，等效媒质理论是分析超材料吸波体吸收机理常用的方法之一，由于背板全覆铜无透射，可以得到等效阻抗[14]为

根据式(2)可以看到，反射系数接近0 时可以实现高吸收率. 因此，在吸波体的设计中尽量保证z(ω)=1.

由于超材料吸波体背板采用全金属铜，无透射发生，入射的电磁波除吸收外全部被反射. 因此，根据仿真的S 参数编写程序可以得到吸波体等效阻抗的实部和虚部. 如图4(a)所示，黑色和红色分别代表等效阻抗的实部和虚部，在10～18 GHz 的区间内红色的线接近0，黑色的线接近1. 因此，在该频段内的等效阻抗接近1，实现与自由空间阻抗匹配，保证电磁波的完美吸收. 由于等效阻抗不等于1，所以吸收率无法达到100%，只能无限接近.

除此之外，超材料吸波体的本构参数也是佐证吸收机理的一种重要手段. 由于背面铜板的存在，结构本身无透射发生，无法利用等效媒质理论进行S 参数反演求得本构参数，等效介电常数ε(ω)和磁导率µ(ω)新的计算公式[15]为：

由图4(b)和(c)可以看到ε(ω)和 µ(ω)的实部在吸收带宽内基本相同，并且都接近于0，使得吸波体与自由空间实现阻抗匹配，曲线的变化证实了电场和磁场对吸收带宽具有调控作用. 本构参数的虚部表示超材料吸波体对入射电磁波的损耗，由图4(b)和(c)还可以看到在吸收频带范围内损耗较大，实现了良好的吸波特性.

图4 超材料吸波体等效参数Fig. 4 Equivalent parameters of metamaterial absorber

电磁超材料吸波体的损耗一般分为介质损耗和欧姆损耗. 图5 对比展示了FR4 介质在有无损耗时吸收率随频率的变化曲线，两条曲线的走势基本一致，但在10～18 GHz 范围内，有耗的FR4 介质基板吸收率高于无耗基板，并且吸收率总体均高于80%.因此，该吸波体结构存在一定的介质损耗，为进一步验证是否存在顶层金属的欧姆损耗，利用不同金属材料Cu 与PEC 进行对比得到图6，图中两条曲线重合，即顶层金属的欧姆损耗很小. 除此之外，在图3表面电流分析中可以发现介质顶层与底层之间形成的回路通过激发磁谐振同样是消耗电磁波的一种重要方式，总之该超材料吸波体的损耗方式不单一，包括介质损耗、磁谐振损耗以及少部分的欧姆损耗. 由于介质存在一定阻抗，并且前面已经证明本构参数的虚部是对电磁波进行吸收损耗的主要原因，因此，这里的超材料吸波体主要是通过介质损耗产生电磁吸收. 这就意味着介质材料的介电常数与磁导率对吸收率会产生一定的影响，图7 对不同介电常数的材料进行了仿真分析，同时表2 给出了具体材料名称、相对带宽等. 根据表2 结果可以充分地验证上述猜想，介电常数的变化对吸收率的影响较大，并且与谐振频率呈现反比关系，随着基底介电常数的增加，整体的吸收频段向低频偏移，吸收带宽明显减少，吸收率由90%逐渐降为80%.

表2 不同介质基板的仿真结果Tab. 2 Simulation results of different dielectric substrates

图5 FR4 基板在有无损耗下的吸收率Fig. 5 Absorptivity of FR4 substrate with or without loss

图6 不同金属材料下的吸收率Fig. 6 Absorptivity of different metal materials

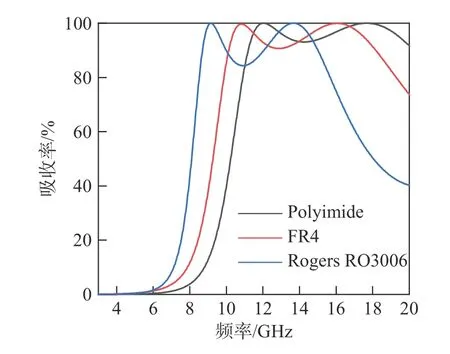
图7 不同基底材料下的吸收率Fig. 7 Absorptivity of different substrate materials

2.2 等效电路分析

图8 展示了超材料吸波体的等效电路模型，顶层的两组对称弯曲金属条等效为两个串联的RLC 电路，同时并联在一起与介质板的等效阻抗相连，图中Zh表示介质板的等效阻抗，Cg1和Cg2分别表示每组金属条之间断裂部分的等效电容.

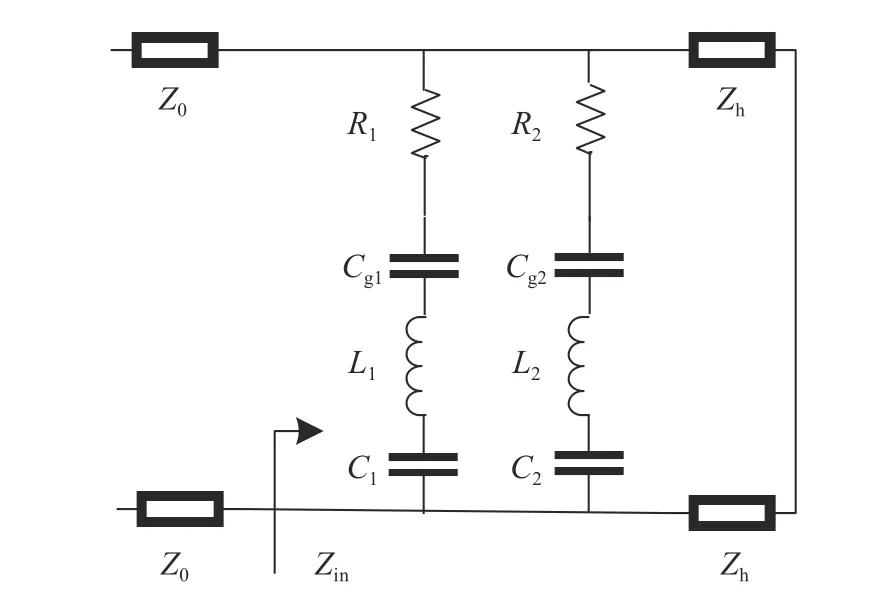
图8 等效电路模型Fig. 8 Equivalent circuit model

根据等效电路理论可以得到每组金属条的等效电感[16]：

式中，m表示不同组金属条之间的距离. 开口处的等效电容以及电阻可以通过公式(13)和(14)计算：

式中：A表示金属截面的横截面积； ε表示介质的等效介电常数；G表示金属条断裂处之间的距离； ρ表示金属的电导率. 因此，可以通过上述的公式得到超材料吸波体的等效参数，如表3 所示. 利用ADS 对等效电路进行优化，如图9 所示，同样存在两个谐振点，带宽范围与曲线走势和CST 的结果基本一致，验证了等效电路方法的可行性.

表3 等效参数值Tab. 3 Equivalent parameter value

图9 等效电路ADS 和CST 仿真对比图Fig. 9 Comparison of equivalent circuit simulation between ADS and CST

3 实验分析

通过理论与仿真对超材料吸波体的吸收特性有了深入的了解后，随即进行实际加工，目的是更进一步验证吸波体的吸收性能. 如表4 所示，对比现有的吸波体，本文设计的吸波体具有更小的尺寸和更宽的入射角. 由于小单元结构不易测量，为方便实测，利用印刷电路板(printed circuit board, PCB)的方法制作了60×60 个单元结构组成的超材料吸波体阵列，总体尺寸达到18 cm×18 cm，如图10(a)所示，固定在暗室中的一侧. 同时，需要两个工作在1～18 GHz 的宽带双脊喇叭天线作为电磁波的收发端，并将两者并排放置面向吸波体，与其保持同一水平面. 将两个喇叭天线与Agilent N5244A 矢量网络分析仪连接，并保证测试板与喇叭天线之间满足远场条件.

表4 本文与现有超材料吸波体的比较Tab. 4 Comparison of metamaterial absorbers between thispaper and the existing ones

图10 不同极化方式与不同入射角下的吸收率测量环境与结果Fig. 10 Measurement environment and results of absorption rates with different polarization modes and incident angles

为验证不同极化方式下吸波体的高吸收率，将两个双脊喇叭天线的方向均旋转0°和90°，实测垂直入射时TE、TM 极化方向下的S 参数，根据式(2)得到吸收率曲线. 图10(b)、(c)分别展示了TE 与TM 极化方式下吸收率实测的结果，将其与仿真结果对比发现，曲线的走势基本一致，在10.8 GHz 和16 GHz处出现两个吸收峰. 但由于加工精度和测量中的环境干扰误差不可避免，因此得到的实测曲线并不光滑，存在噪声干扰，同时高频谐振点附近均略有误差，产生偏移，但超材料吸波体总体吸收带宽与仿真近似.

随后，利用转台转动不同的角度实测出吸波体在不同入射角下的S 参数，从而得到吸收率曲线. 如图10(d)、(e)所示，不同极化方式下均能看到10.8 GHz和16 GHz 两个吸收峰. 随着电磁波入射角的不断增加，吸收带宽逐渐减少，10.8 GHz 谐振点吸收率不变，但16 GHz 的谐振点受角度稳定性影响较大，当入射角等于45°时，除个别点存在误差外，吸收率均保持在80%以上，与仿真结果一致，即具有良好的角度稳定性.

4 结 论

在传统吸波体结构的基础上，引入两组对称弯曲的金属条设计了一种新型超材料吸波体结构. 在10～18 GHz 范围内实现超宽带吸收，相对带宽达到57.1%，结构单元尺寸为0.1 λL，厚度为0.062 λL. 当电磁波入射角为45°时，超材料吸波体的吸收率仍能保持80%以上，满足小型化电子器件辐射抑制的需求通过理论分析，采用等效电路与本构参数法验证其吸波机理，0°～45°入射角下TE、TM 极化波的吸收率实测结果与仿真结果吻合，表明超材料吸波体具.有极化不敏感与角度稳定性的特点. 目前，尚未在实测部分验证其电磁干扰抑制能力，后续工作中可以结合辐射源开展进一步研究.