圆极化复用型多功能超构表面研究进展
袁乐眙 张狂 王禹翔 吴群
(哈尔滨工业大学电子与信息工程学院,哈尔滨 150001)
引 言
超构表面(Metasurface)是一种由周期/准周期性分布的电磁散射体组合而成的二维结构,通过对亚波长单元电磁响应的精确设计,可实现对电磁波的幅度、相位、极化等特性的人工调控[1]. 结合超薄超轻、易于共形的结构优势,具有特定电磁调控能力的超构表面为新一代信息技术的发展提供了全新的平台[2-4]. 近年来,在集成化与小型化无线通信系统快速发展的背景下,功能多样化的超构表面被广泛地研究与应用. 目前,通过区域划分[5-6]、共享口径[7]、频率复用[8-10]、机械调控[11]、化学激励[12]等方法均可对单一超构表面集成多个不同功能. 然而,利用这些方法设计的多功能超构表面均基于几何相位对圆极化波的调控作用,根据几何相位的物理来源可知,通过旋转单元结构在圆极化电磁波传播过程中引入的相位突变大小是旋转角度的二倍,并且仅作用于交叉极化分量中[13-14]. 因此,在同一交叉极化传输通道中实现的多个功能之间存在难以避免的耦合与干扰. 由此可知,利用入射端与出射端极化状态的组合在不同极化传输通道中加载多个功能,即基于极化通道复用的波前调控方法,可实现低耦合、高效率的多功能集成化设计. 除此之外,将入射与出射端极化状态的多重组合作为超构表面的多功能转换开关,有效降低了无源超构器件的设计复杂度和加工成本,为小型化、集成化的电磁调控器件提供了理论基础. 从极化复用的角度而言,基于圆极化电磁波的正交隔离性[15-16],通过入射端与出射端极化状态的组合,可存在四个可用的圆极化传输通道,即左旋圆极化(left handed circular polarization, LHCP)发射-LHCP 接收(L-L 同极化传输通道)、LHCP 发射-右旋圆极化(right-handed circular polarization, LHCP)接收(L-R 交叉极化传输通道)、RHCP 发射-LHCP 接收(R-L 交叉极化传输通道)、RHCP 发射-RHCP 接收(R-R 同极化传输通道). 几何相位源于入射圆极化电磁波转换为其交叉极化出射波的过程中,因此基于几何相位的超构表面目前仅能工作在两个交叉极化传输通道,并实现共轭对称的相位函数[17]. 与此同时,同极化波虽然会传输电磁能量,但无法通过几何相位实现波前调控,这极大程度地限制了圆极化传输通道的复用程度和多功能的集成数量.
因此,如何充分利用四条圆极化传输通道,实现单一超构器件的多样化功能集成,并以尽可能高的能量利用率实现对圆极化波的人工调控,是目前基于几何相位超构表面调控圆极化电磁波亟待解决的理论问题. 本文将介绍本课题组关于极化复用型超构表面的研究进展和相关应用成果. 首先针对几何相位在正交圆极化波作用下的共轭对称响应,通过分析超构表面的等效琼斯矩阵,提出了交叉极化去耦合调控方法,并设计了汇聚/涡旋超构透镜,实现了交叉极化复用的双功能集成. 其次,通过分析传播相位对透射场中同极化与交叉极化分量的幅相调控作用,提出了三通道复用的多功能超构表面设计方法,实现了多模式涡旋波束的高纯度集成. 最后,通过引入手性诱导相位,设计了四通道偏折超构透镜,实现了对圆极化全通道的同步人工调控. 本文所提出的极化复用多功能超构透镜为扩展通信系统容量、提高信息传输速率提供了理论基础.
1 交叉极化双通道的去耦合调控
基于几何相位的超构表面是调控圆极化电磁波波前的传统方法,然而其在正交圆极化波作用下所产生的共轭相位响应是对交叉极化分量实现波前复用的主要限制. 因此,为了实现交叉极化双通道的去耦合调控,利用超构表面的等效琼斯矩阵表征圆极化入射波与出射波之间的传输关系,将超构表面单元结构等效为理想双折射波片,计算可得,超构表面单元沿x、y方向的相位延迟和旋转角度可分别表示为[18]:

式中:(x,y)表示超构表面所在平面的离散化位置坐标;φxx、φyy分别表示处于该位置的单元需分别提供沿x和y方向的相位延迟,即超构单元所需引入的传播相位响应;θ 为单元所提供的旋转角度,即几何相位响应;Φ+(x,y) 和Φ-(x,y) 分别表示在LHCP 和RHCP电磁波的入射条件下,超构表面所需引入的两个独立相位分布函数. 可以看到,通过双折射单元所提供的传播相位可对几何相位的共轭对称中心产生有效的修饰作用,公式(1)~(3)给出了设计具有去耦合交叉极化波前的超构表面设计方法,即通过结合传播相位对正交圆极化的一致性作用和几何相位的共轭作用,便可在两个交叉极化通道中实现独立的相位分布函数.
本文根据微波滤波器理论和小型化频率选择表面原理[19-20],设计了一种双折射超构单元结构,由五层金属、四层介质组成,周期大小a= 8.8 mm,其结构示意图如图1 所示. 单元的奇数层为金属矩形贴片结构,其宽度为px,长度为py. 为了小型化设计,贴片上有三条平行且尺寸完全相同的矩形缝隙,缝隙长宽分别为wx和wy,间距为g. 偶数层金属为网格层结构,为了保证单元结构的旋转不敏感特性,网格设置为圆形缝隙,网格层缝隙半径r= 3 mm. 四层介质具有完全相同的厚度和材料特性,介电常数εr= 3.5,厚度设置为h= 1 mm.

图1 双折射超构单元结构示意图Fig. 1 The topological structure schematic of dual-refracting meta-atom
图2 给出了单元结构的线极化幅度和相位响应曲线. 单元在沿x和y方向的线极化入射波的分别照射下,其透射场只存在与入射波极化一致的线极化分量txx和tyy,同极化幅值在工作频点10 GHz 处均可接近于1,而线极化交叉极化传输系数txy和tyx,在整个带宽范围内幅值均为0. 与此同时,两个同极化相位响应可在8~12 GHz 的宽频段范围内保持均匀变化,并且在工作频点10 GHz 附近线极化相位响应差值能够稳定地保持在180°左右,保证了圆极化100%的交叉极化转换率.

图2 双折射超构单元结构的线极化响应曲线Fig. 2 The simulated phase profiles of dualrefracting meta-atom
通过对单元矩形贴片的长宽尺寸进行优化,挑选了24 个具有15°相位梯度的单元结构组成单元库,为交叉极化复用的涡旋/汇聚双功能超构透镜设计打下基础,其工作原理示意图如图3 所示.
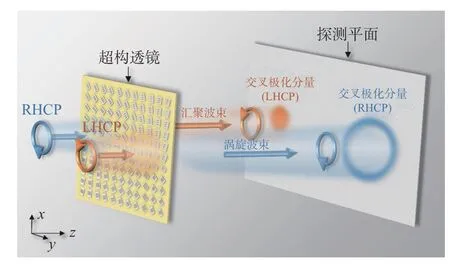
图3 双功能超透镜的原理示意图Fig. 3 Schematic of bi-functional metasurface lens
根据螺旋相位板和光学凸透镜的累积光程分布,涡旋波束和汇聚波束的空间相位分布函数可以分别表示为:

式中:l表示涡旋波束携带轨道角动量(orbital angular momentum, OAM)的拓扑电荷数,l= 2;f表示汇聚波束的焦距,f= 5λ0(150 mm);λ0表示工作波长(中心频点设置为10 GHz,即工作波长λ0= 30 mm). 为验证交叉极化解耦合调控方法的有效性,对该超构透镜进行了实物加工和实验测试,其加工样品如图4 所示.

图4 双功能超透镜的加工样品照片Fig. 4 Picture of bi-functional metasurface sample
图5 给出了该超构透镜在LHCP 波照射下,其交叉极化能量和相位分布的实测结果. 可以看出,在左旋交叉极化透射场中,沿着电磁波的传播方向,能量关于中心轴对称分布,并且随着传播距离的增大能量分布呈发散状态. 在垂直于传播方向的xoy横截面(z= 5λ0)内,电磁能量呈现面包圈式的环形分布状态,对应的相位呈现l× 2π (l= 2)螺旋分布,证明了该超构透镜能在左旋波的照射下,利用交叉极化分量产生一个携带OAM 数为2 的涡旋波束.

图5 LHCP 波作用下双功能超构透镜的交叉极化能量与相位分布Fig. 5 Energy and phase distributions of dual functional meta-lens under LHCP incidence
当入射波转换为RHCP 时,超构透镜的交叉极化透射场能量分布及相位分布情况如图6 所示. 在电磁波的传播方向内,能量明显汇聚于z= 5λ0位置附近,并且在该位置的xoy横截面内电磁能量聚集于中心一点呈焦点状,相位分布由中心向四周呈环状分布,符合汇聚波束的波前分布规律. 实测结果证明,该超构透镜能够在正交圆极化波的作用下,分别利用其交叉极化分量产生涡旋波束和汇聚波束,实现了交叉极化复用的双功能集成,证明了交叉极化解耦合调控方法可有效地突破几何相位的对称缺陷.
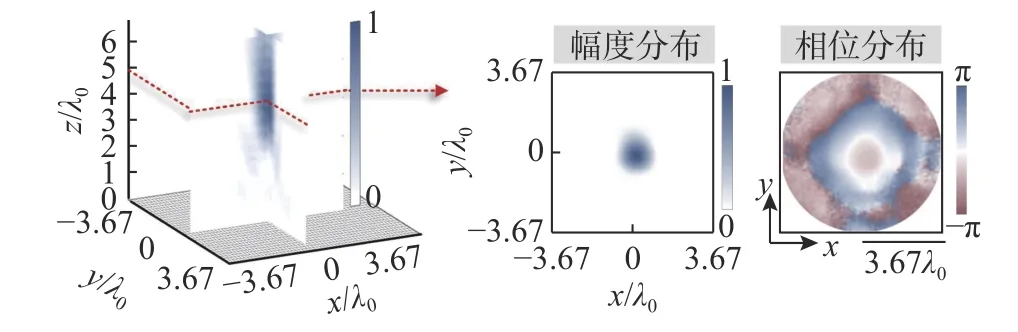
图6 RHCP 波作用下双功能超构透镜的交叉极化能量与相位分布Fig. 6 Energy and phase distributions of dual functional meta-lens under RHCP incidence
2 同/交叉极化复用三通道的独立调控


沿用上节所提出的双折射多层级联型单元结构,并通过挑选正交线极化相位差值均为π/2 的24个单元作为单元库,为构建三通道复用的多功能超构表面提供理论基础,图7 为三通道复用的涡旋波束集成型超构透镜工作原理示意图.

图7 三模式涡旋集成超构透镜的原理示意图Fig. 7 Schematic of tri-mode vortex integration meta-lens
利用圆极化的正交隔离特性,通过传播相位将涡旋波束l= 2 的相位分布ΦOAM,l=2加载于同极化传输通道:

式中,ΦLL/ΦRR表示在LHCP/RHCP 电磁波入射时,同极化透射场中的相位分布. 与此同时,利用几何相位将涡旋波束l= ±1 的相位分布ΦOAM,l=±1分别加载于两个交叉极化传输通道,即有
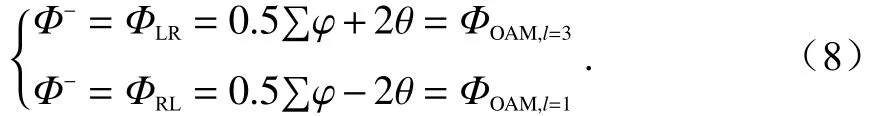
式中,ΦLR/ΦRL表示在LHCP/RHCP 电磁波入射时交叉极化透射场中的相位分布. 基于此,位于(x,y)位置处的单元需提供的传播相位与几何相位响应分别为:

根据式(9)~(11)设计的超构表面由25×25 个单元结构组合而成. 图8 所示为该超构透镜的实物加工照片,与仿真设计完全一致,实物透镜同样由25×25 个单元构成.

图8 三模式涡旋集成超构透镜的加工样品Fig. 8 Picture of tri-mode vortex integration meta-lens
图9(a)所示为超构透镜在不同圆极化传输通道中产生涡旋波束的环状能量分布仿真结果(左侧一列) 与测试结果(右侧一列),当涡旋波束携带OAM模式数分别为l= 1、2、3 时,在xoy横截面内,携带不同拓扑电荷数OAM 的涡旋波束暗斑直径均随着l的增大而增大,有效证明了涡旋波束的传播特性,即l越大涡旋波前发散情况越严重,与理论设计相符合. 结合图9(b)给出的涡旋波束相位分布的仿真(左侧一列)及测试(右侧一列)结果可知,携带不同拓扑电荷数OAM 的涡旋波束相位严格满足l× 2 π的分布规律. 同时可看到,测试结果与仿真结果吻合较好,能量的环状分布与相位的螺旋状分布均能有效证明不同模式OAM 的产生. 通过仿真和测试结果可以确定,当入射波为LHCP 时,其同极化传输通道L-L中实现了OAM 为l= 2 的涡旋波束,对应交叉极化通道L-R 中实现了OAM 为l= 3 的涡旋波束;当入射波为RHCP 时,其同极化传输通道R-R 中同样实现了OAM 为l= 2 的涡旋波束,且其交叉极化通道R-L中实现了OAM 为l= 1 的涡旋波束,符合预期理论设计,验证了三通道极化复用的可行性.

图9 携带OAM 模式l=1, 2, 3 的涡旋波束仿真(左列)及测试(右列)结果Fig. 9 Simulated(left) and measured(right) results of vortex beam carrying OAM modes with l=1, 2, 3 respectively
为进一步分析超构表面在不同圆极化传输通道中产生涡旋波束的性能,对透射场中所产生的涡旋波束OAM 纯度进行计算和分析. OAM 纯度定义为预期OAM 模式在总模式中所占比例,根据xoy平面内相位分布的实测结果对OAM 的纯度进行定量计算[23]:

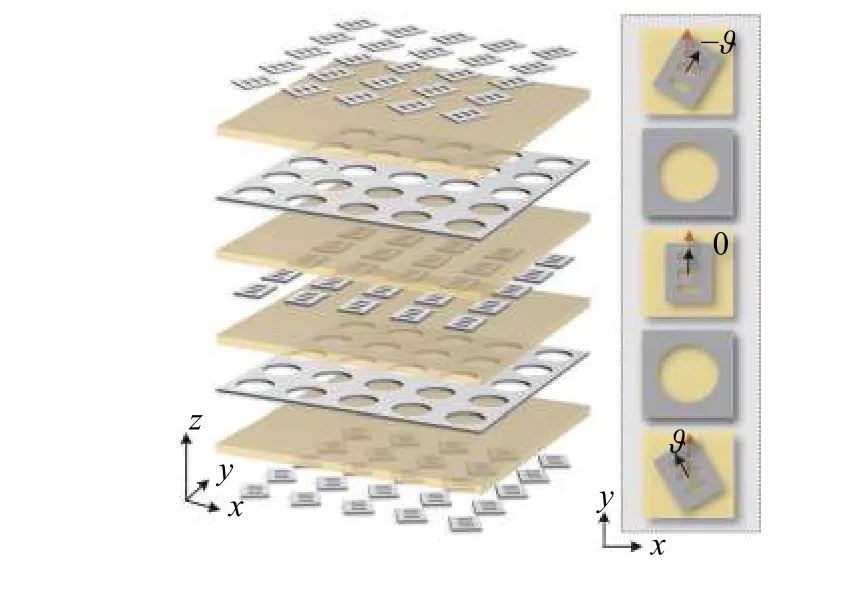
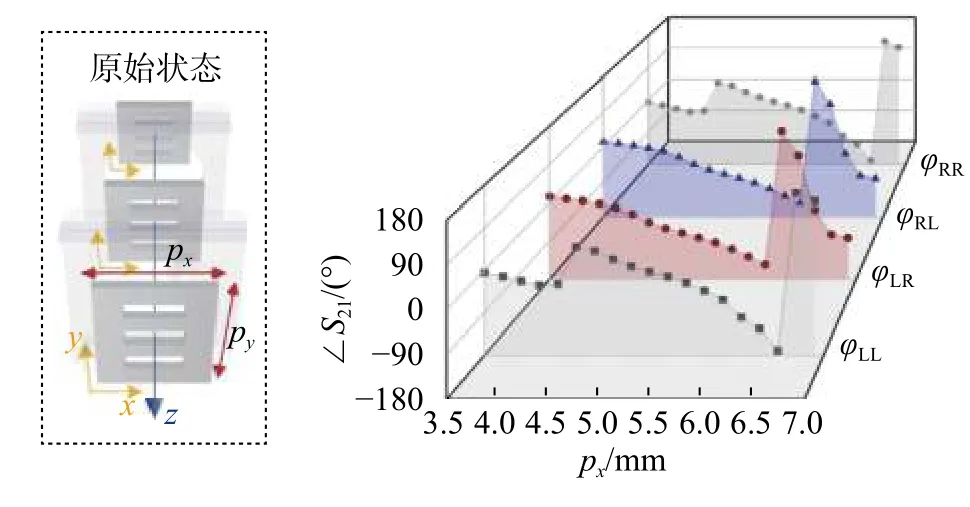
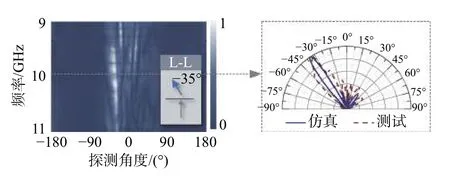
式中,ψ(φ)表示探测平面内沿方位角方向的空间相位分布. 若考虑OAM 模式数范围为la~lb,待测涡旋波束的模式数为l0且有la 根据式(14) 可得超构表面所产生的携带OAM模式数为l= 1、2、3 的涡旋波束在带宽9.5 ~10.5 GHz内的模式纯度,如图10 所示. 可以看出,在工作频点10 GHz,模式数为l= 1、2、3 的OAM 纯度分别可达到88.6%、84.6%、82.7%,且在带宽范围内,三种涡旋波束均能保持较高的模式纯度. 这一结果证明了该超构表面能够在不同圆极化传输通道中实现高纯度的整数模式涡旋波束,有效验证了圆极化三通道复用的理论可行性. 图10 三种OAM 模式的纯度分析Fig. 10 Purity analysis of 3 OAM modes 由于传播相位不具有手性响应,因此圆极化的两个同极化传输通道无法被加载独立的波前分布.因此,本文通过推导普适的琼斯矩阵分析传播相位、手性诱导相位、几何相位对圆极化四个传输通道间相干耦合性的调控作用,从而在不同通道加载独立相位分布函数,实现四通道复用波前调控[24]. 首先从宏观角度分析,当入射电磁波穿过超构表面模型后,可产生四个极化传输通道,为了实现四个传输通道的独立调控,需在四个通道中分别加载不同波束的相位分布函数FLL(x,y)、FLR(x,y)、FRL(x,y)、FRR(x,y),可得到超构表面整体的线极化基琼斯矩阵模型如下: 从微观角度分析,对于任意不具有旋转对称特性的亚波长单元结构而言,其普适的复琼斯矩阵可表示为 根据以上分析可知,通过调节亚波长单元结构所引入的传播相位、几何相位以及手性诱导相位响应,结合四个已确定的相位分布函数构建多功能集成型超构表面,实现对圆极化全通道的波前人工调控. 即通过综合三种相位对正交圆极化电磁波的共同作用,解耦传输系数四个相位响应的相干耦合性,从而实现对圆极化全通道的独立调控 为实现手性诱导相位,延用上节所提出的多层级联型单元结构,通过调节各层贴片间的相对旋转角度在原结构中引入手性特征,单元阵列示意图如图11 所示. 将该单元等效为由三个完全相同的单层双折射矩形波片级联而成的传输系统,其中每层波片的旋转角度分别为-ϑ、0、ϑ,此处定义ϑ为内部旋转角度. 因此,多层单元的等效级联网络的四个圆极化传输系数可表示为: 图11 具有手性特征的单元结构拓扑示意图Fig. 11 Schematic of meta-atom with chiral characteristic 式中,t0xx和t0yy分别表示单层矩形贴片理想模型的双折射传输系数. 首先,将单元矩形贴片层的宽度px和长度py作为传播相位的调控自由度,图12 左侧部分所示为该单元只具有传播相位调控自由度时的结构示意图. 固定py,px从3.5 mm 增大至7 mm 时,传输系数相位响应的仿真结果如图12 右侧部分所示,同极化和交叉极化通道具有不同的传播相位响应,趋势也随着px的增大而改变,两个同极化相位始终一致,交叉极化相位同样保持一致. 图12 单元的传播相位响应验证Fig. 12 Verification of propagation phase of meta-atom 其次,将单元贴片的相对转角作为调节手性诱导相位的结构自由度,图13 左侧部分给出了该单元只具有手性诱导相位调控自由度时的结构示意图.当ϑ从-90°均匀变化至90°时,两条同极化相位曲线产生了完全相反的变化趋势,如图13 右半侧部分所示,即两个同极化相位的相干性被打破,且解耦的两个同极化相位响应可分别覆盖2π 范围. 在此过程中,两个交叉极化通道的相位响应虽然有所改变,但两条曲线趋势则保持一致. 图13 单元的手性诱导相位响应验证Fig. 13 Verification of chirality-assisted phase of meta-atom 最后,调控几何相位的结构自由度是单元结构的整体旋转角度,即三层金属贴片的同步旋转角度.图14 左侧部分为该单元只有具有几何相位调控自由度时的结构示意图. 通过图14 右侧部分给出的传输系数曲线可知,随着外部旋转角度θ 从-90°增大至90°,两个交叉极化相位响应产生了共轭对称的变化趋势,而两条同极化相位曲线基本保持不变,这是几何相位调控方法能够有效控制交叉极化分量的基础条件. 图14 单元的几何相位响应验证Fig. 14 Verification of geometric phase of meta-atom 通过以上的验证可知,四个圆极化传输通道的相位响应可通过单元矩形贴片的长宽尺寸、内部转角和外部转角进行调节. 传播相位、手性诱导相位、几何相位可分别对圆极化四个传输系数之间的相干性产生去耦调控作用,并且三种相位调控方法可同时通过独立的结构自由度实现,有效地验证了三种相位工作机理的兼容性和可行性,为圆极化四通道的波前独立调控设计打下理论基础. 本文所设计的四通道偏折波束超构透镜的示意图如图15 所示,在LHCP 和RHCP 电磁波的入射下,透射场中的四个圆极化传输通道中可分别产生具有不同传播方向的偏折波束. 图15 四通道偏折波束超构透镜示意图Fig. 15 Schematic of quadruplex-angle refraction meta-lens 根据广义折射定律,四个偏转出射波束的空间相位分布函数表示为 图16 四通道偏折波束超构透镜的加工样品照片Fig. 16 Picture of quadruplex-angle refraction meta-lens 图17 所示为该超构透镜在LHCP 电磁波的照射下,工作带宽9~11 GHz 内的同极化远场电场测试结果,越是明亮的区域表示远场场值越强. 可以看出,同极化出射波的远场电场峰值出现在方位角-35°左右,并且在整个工作带宽9~11 GHz 内,远场模式下的偏转角度会随频率的变化稍有偏移,这是由色散现象引起的. 图17 L-L 通道中出射方向与法线夹角为-35°的偏折波束Fig. 17 Refracted beam with angle of -35° in L-L channel 图18 所示为该超构透镜在LHCP 入射条件下的交叉极化透射分量在远场的电场强度分布结果,同样在工作带宽9 ~ 11 GHz 内,最为明亮的场值分布区域出现在方位角0°附近,在透射波垂直出射的情况下,其峰值不随频率的变化而变化. 在工作频点10 GHz 处的远场方向图由右侧的极坐标图表示,其仿真与测试的曲线峰值均能很好地证明左旋交叉极化出射波能够维持入射波的传播方向,沿+z轴不偏折出射. 图18 L-R 通道中出射方向与法线夹角为0°的偏折波束Fig. 18 Refracted beam with angle of 0° in L-R channel 当该超构透镜的入射电磁波为RHCP 时,其同极化和交叉极化出射波束在工作带宽9~11 GHz 内的远场场值分布情况如图19 所示. 可以看出:远场方向图的峰值出现在+58°附近,由于偏折角度较大,其有效的工作带宽大致范围为9.5~10.2 GHz;而在其他范围内,最为明亮的场值分布区域则出现在0°附近. 通过其在工作频点10 GHz 处的仿真和测试远场分布曲线可知,主瓣方向为+58°,同时其旁瓣的场值也高于其他传输通道中的偏折波束. 图19 R-L 通道中出射方向与法线夹角为56°的偏折波束Fig. 19 Refracted beam with angle of 56° in R-L channel 由图20 可观察得到,在对应的右旋同极化透射场中,波束在工作带宽9 ~11 GHz 内均能保持良好的-16°偏折特性,且在工作频点处的远场场值曲线也能很好地与理论设计相吻合. 值得注意的是,在测试过程中,由于暗室环境中存在难以避免的反射、散射噪声,因此测试结果中的远场场值曲线不如仿真结果的平滑. 但测试曲线的峰值均能较好地符合理论仿真结果,证明该超构透镜能够在圆极化的四个传输通道中加载四个具有独立传播方向的偏折波束,验证了圆极化全通道调控方法的理论可行性. 图20 R-R 通道中出射方向与法线夹角为-16°的偏折波束Fig. 20 Refracted beam with angle of -16° in R-R channel 本文简要回顾了本课题组关于圆极化复用型多功能超构表面的研究工作. 从几何相位的共轭对称响应出发,基于理想超构表面的等效琼斯矩阵模型,推导了交叉极化的去耦合调控方法,设计了涡旋/汇聚双功能超构表面,实现了圆极化波的双通道复用调控. 进一步利用传播相位对同极化与交叉极化分量的幅相调控作用,结合圆极化状态的正交隔离特性,实现了携带三种不同模式OAM 的涡旋波束集成,验证了三通道复用型多功能超构表面的有效性.最后,通过引入手性诱导相位,结合传播相位与几何相位对正交圆极化波的共同作用,设计了四通道偏折超构透镜,实现了对圆极化传输通道的最大化拓展. 仿真及实测结果能很好地与理论设计保持一致,有效证明了本文所提出的系列极化复用波前调控方法的理论可行性,为现代通信系统的信道扩容、速率提升提供了理论指导.

3 圆极化四(全)通道的复用调控



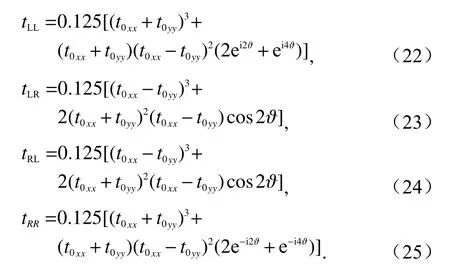








4 结 论

