基于智能反射面的无线抗干扰通信方法

孙艺夫 安康 朱勇刚 李程 李勇

（国防科技大学第六十三研究所，南京 210007）

引 言

信息化战争条件下，制信息权是决定战场胜负的关键因素之一. 由于无线信道的开放性，军用无线通信系统不仅面临各种复杂、时变、未知的自然干扰，而且面临窃听者攻击、数据篡改攻击以及干扰攻击等对抗性电磁威胁[1-3]. 如何提高军用无线通信系统的战场生存能力，是打赢信息化局部战争首先需要解决的焦点和难点问题.

传统抗干扰手段主要包括跳频扩频(frequency hopping spread spectrum, FHSS)、直序扩频(direction sequence spread spectrum, DSSS)、自适应功率控制技术等[4]. 近年来，随着干扰技术的不断发展，特别是动态干扰、“灵巧”式干扰、认知干扰等高效干扰技术的出现，使得传统抗干扰技术受到日益严峻的挑战[5].为了应对智能化干扰威胁，研究者从“以智能对抗智能”的角度出发，提出了基于博弈论的抗干扰方法.博弈论需要以已知的干扰策略集为基础，建立起干扰者和传输者之间决策互动模型. 文献[6-9]将抗干扰信道决策问题建模为零和博弈，以得到最佳信道选择策略；文献[10-13]将基于功率控制的抗干扰决策问题建模为Stackelberg 博弈. 然而，上述方法均是以已知干扰策略为前提的，这在实际应用中难以实现. 为了解决干扰策略未知带来的抗干扰决策问题，研究人员将Q 学习等无模型强化学习(reinforcement learning, RL)算法应用于抗干扰决策[14-15]. 文献[16-18]应用Q 学习算法获取概率干扰下的最佳跳频模式.但是，Q 学习等算法存在的显著缺点是：当状态空间和行为空间较大或者干扰环境较复杂时，其收敛时间显著增长，严重影响了该类算法在时变环境中的可用性. 受深度强化学习(deep reinforcement learning,DRL)在其他领域的启发[19]，文献[20-22] 使用DRL解决了上述Q 学习的“维度灾难”问题. 但是，DRL 算法往往需要大量样本来训练神经网络，计算复杂度大且训练时间长，导致该算法实用性不强. 随着干扰智能化程度不断提高，基于RL 或DRL 的信道选择抗干扰方法往往难以准确预测和躲避干扰，导致频谱利用率降低和多用户频谱接入协同困难.

天线阵列提供的空间分集可以有效提高接收信干噪比(signal-to-interference-plus-noise ratio, SINR)，因此多天线技术被认为是一种有效的抗干扰技术[23].当前多天线技术可以分为发射阵列设计和接收阵列设计. 文献[24-26]提出在发射端设计最佳波束以获取空间分集对抗干扰，但波束成形需要大量发射天线. 除此之外，多天线技术还被应用在接收端以消除干扰. 文献[27-28]提出调整接收端滤波器使得多天线在空间零陷中接收干扰信号，从而使得干扰功率增益为零以消除干扰. 虽然多天线技术在其他方法失效的情况下仍然有效，但由于接收端滤波器也可以抑制有用信号，因此需要最佳的接收滤波器设计.

针对上述传统抗干扰方式“以变制扰”的劣势，本文提出使用内生安全的思想去抵抗干扰攻击. 广义内生安全(endogenous safety and security，ESSE)概念最早来源于网络空间，是指目标对象在一定约束条件下，不依赖关于攻击者的先验知识，与附加型安全措施不相关或弱相关，主要凭借本体构造设计或算法的内源性效应来获得针对其ESSE 问题的广义不确定扰动之鲁棒控制能力. ESSE 思路在5G/6G 移动通信、光纤通信领域安全体制构建中得到了应用[29]. 军事无线抗干扰通信体制下的ESSE 架构必须基于无线信道电磁环境特征设计. 无线通信的本质是开放式的无线信道，无线信道的内生属性是信道特征. 以信息超材料赋能的数字可编程智能反射面(intelligent reflecting surface, IRS)利用材料科学与信息科学交叉融合产生的非线性增益强化赋能ESSE，为未来无线通信对抗和博弈领域提供了重要的理论、技术和方法支撑，在无线抗干扰通信中得到了学术和产业界的广泛关注[30-31]. 因此，为实现高频谱和能量效率、低复杂度以及高可行性的内生抗干扰手段，本文提出利用IRS 作为实现内生抗干扰的解决方案. IRS 是一种具有人工设计的结构并呈现出天然材料所不具备的超常物理性质的信息超材料表面，在超表面单元与数字信息之间建立联系，通过各种可调手段对电磁波各参数进行实时动态调控，实现如波束扫描、极化转换、幅度/相位调制等不同功能[31-33]. 信息超材料的发展促进了物理空间和信息空间的有机统一，实现了无线信道环境的按需可重构.文献[34]通过引入IRS，使得通信网络的覆盖范围得到大幅提升. 文献[35]进一步考虑了实际系统中的离散相位设定，调节IRS 离散相移提高系统功率效率. 文献[36-38]考虑了利用IRS 提高物理层安全，其中文献[36] 在安全容量的限制下最小化传输功率，而文献[37-38]在功率限制下最大化安全容量. 文献[39]进一步联合人工噪声和IRS 提升物理层安全性能. 文献[40]首次提出了利用IRS 去对抗干扰攻击，以实现总传输速率最大化，但是其忽略了IRS 也可以反射干扰信号，而在本文我们进一步考虑该实际场景.

本文针对IRS 辅助的无线内生抗干扰通信系统开展研究，其中多天线通信发射机在多天线干扰机存在的场景下，借助IRS 协同进行可靠、低功率内生抗干扰通信. 相对传统抗干扰方案，所提方案以固定频点和低功率对抗干扰攻击，使得频谱和功率效率得到大幅度提升. 相对基于博弈论和RL 的智能抗干扰方案，所提方案不以获知干扰模型为前提，且不需要训练时间，实时性和可行性更强. 相对传统的空域抗干扰，所提方案能够对信道按需重构，且能耗更低，不需要大量天线与射频端部署. 本文的主要创新点可归纳如下：1)针对高功率压制干扰或智能干扰威胁，提出了一种基于IRS 的无线内生抗干扰通信方法. 具体来说，在传统无线通信系统中引入IRS，通过联合优化传输波束和IRS 相移使得传输功率最小化，以实现在固定频点以低功率对抗干扰攻击，进而提升频谱和功率效率，最终实现“以不变应万变”的内生抗干扰通信. 2)针对联合优化求解难的问题，我们提出基于交替最优化算法和半定松弛(semidefinite relaxation, SDR)方法交替求解最优解. 3)针对优化模型复杂度高的问题，提出利用拉格朗日对偶函数求解发射波束的闭式解. 4)针对实际系统中干扰机传输信道状态信息(channel state information, CSI)难以准确获取问题，提出了一种经验算法，利用三角不等式和最大率传输(maximum ratio transmission, MRT)准则分别计算IRS 相移和最佳波束，在无需CSI 条件下保证了抗干扰通信的可靠性.

1 系统模型和问题建模

1.1 系统模型

1.2 问题建模

在接收机的SINR 大于阈值的限制条件下，通过最优发射波束和IRS 相移联合设计以实现发射功率最小化. 发射功率最小化意味着利用最小功率对抗干扰功率，即在功率有限的条件下，提高干扰容限和功率效率. 对应的最优化问题被公式化为

图1 基于IRS 的抗干扰通信系统模型Fig. 1 System model of IRS-based anti-jamming communications

2 问题求解

首先，我们提出最优算法，使用SDR 工具求解最优 ωt和 Θ. 然后，为了解决最优算法计算复杂度高的问题，我们提出了低复杂度算法，利用拉格朗日对偶函数求解 ωt的闭式解. 最后，针对干扰机CSI 无法获取的极端场景，提出了基于三角不等式和MRT 准则的经验算法，虽然只能得到次优解，但抗干扰性能非常靠近最优性能.

2.1 最优算法

式(6) 为标准的半正定式(semidefinite programming,SDP)，可以被CVX 工具[41]求解. 最后，传输波束可以通过特征值分解和高斯随机化法求得，由于在文献[34]中详细展示了该方法的步骤，在这里我们为了简洁故省略.

2.1.2 最佳相移设计

进而我们可以得到

2.2 低复杂度算法

在这一小节中，针对上一节最优算法复杂度高的问题，我们提出使用拉格朗日函数求解 ωt∗的闭式解以降低复杂度.

给定相位 Θ，将P2 展开可得P6，其公式如下：

2.3 经验算法

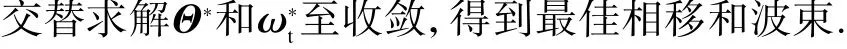
3 结果与分析

本小节利用仿真结果来验证所提算法的有效性.假设发射机和干扰机采用均匀线性阵列(uniform linear array，ULA)，其中发射机和干扰机装备的天线个数分别为M=8,L=2. IRS 采用沿着x轴与y轴分布的均匀矩形阵列(uniform planer array，UPA)，即N=NxNy，其中Nx和Ny分别代表x轴和y轴上的反射元个数. 如图2 所示，发射机-IRS 链路、干扰机-接收机链路、干扰机-IRS 链路和IRS-接收机链路的距离分别为：

图2 位置示意图Fig. 2 Simulation deployment

如图3 所示，我们首先评估了所提三种算法的收敛性. 从图3 可以看出，对于不同的IRS 元个数设定，所有算法都在最多四步内完成收敛. 因此，我们提的三种算法具有很低的复杂度. 进一步观察可以看出，经验算法只需要三步就完成收敛，表明该算法具有最低复杂度.

图3 算法收敛性分析Fig. 3 Convergence of the algorithms

在图4 中，我们分析了不同算法发射功率随干扰功率变化曲线. 结果显示本文所提最佳算法和低复杂度算法均获得最低发射功率. 另外，以Pj=50 dBm为例，未部署IRS 方案需要57.53 dBm 的发射功率，而最佳算法和低复杂度算法仅需26.99 dBm 发射功率，降幅高达29.54 dB. 这说明只进行波束成形无法抵抗高功率干扰，而IRS 相移和波束联合设计却能够抵抗，这使得功率博弈成为可能. 我们通过横向对比还发现，当发射功率固定时，最佳算法和低复杂度算法可对抗的干扰功率较未部署IRS 方案提升约30 dB.比如，当系统最大发射功率为30 dBm 时，未部署IRS 方案仅能对抗28 dBm 的干扰功率，而所提算法可以对抗58 dBm 干扰功率. 这个现象表明所提算法干扰容限大幅度提升，抗干扰能力显著提高. 最后，所提经验算法所需发射功率虽然比最佳算法高了2.62 dB，但是仍然远远低于未部署IRS 方案. 因此，以较低的性能代价换取可行性是可取的. 除此之外，从图4 还可以看出，如果发射波束设计和IRS 相移不是最优的，性能有一定的下降. 因此，联合设计可以使信号功率和干扰功率达到最佳平衡，以实现抗干扰能力最大化.

图4 发射功率随干扰功率变化图Fig. 4 Transmit power vs. jamming power

图5 展示了发射功率与反射元数量N的关系.随着N的增加，引入了IRS 的所有算法所需发射功率均呈下降趋势，最大降幅为8.61 dB，并且前期快而后期趋近平缓. 因此，在实际中，我们可以通过增加反射元数量来降低发射功率，从而提升抗干扰性能和系统能效. 但与此同时，N的增加会导致反射干扰功率提高，那么此时经验算法中忽略干扰信道CSI所造成的影响就会上升，从而拉大该算法与功率下界之间的差距.

图5 发射功率随反射元个数变化图Fig. 5 Transmit power vs. the number of reflecting elements

图6 和图7 分别展示了发射功率与发射机-IRS 垂直距离dvirs、发射者-IRS 水平距离dirs的关系. 在图6 中，所有算法(除未部署IRS 方案)的发射功率都随着dvirs的减小而大幅度下降. 这得益于所采用的联合设计算法，此时接收机信号功率和干扰功率达到了最佳平衡. 综上，减小dvirs能够降低发射功率，提高功率效率和可对抗的干扰功率.

图6 发射功率随发射机-IRS 垂直距离dvirs变化图Fig. 6 Transmit power vs. transmitter-IRS vertical distance,dvirs

在图7 中，所有引入IRS 算法的发射功率随着dirs的增加呈现先增大后减小的趋势，在dirs=40 m 时达到峰值. 分析得到造成该现象的原因为：dirs越接近40 m，IRS 与干扰机的距离就越近，此时路径损耗就越小，反射干扰功率越高. 但因为反射面小型化且为半波长天线，故发射天线靠近IRS 时不会发生对偶现象. 所以，可以通过减小dirs(靠近发射机部署IRS)来降低传输功率. 值得注意的是，在dirs=40 m 的极端情况下，所提算法发射功率比未部署IRS 方案仍有6 dB 的下降，这也体现了所提算法在极端场景下仍能实现抗干扰性能的提升. 另外，随机相位方案的发射功率随着dirs增长呈起伏变化，甚至超过了未部署IRS 方案. 这个现象是随机相位未有效平衡信号功率和干扰功率造成的，也进一步说明动态调整相位的重要性.

图7 发射功率随发射机-IRS 水平距离 dirs变化图Fig. 7 Transmit power vs. transmitter-IRS horizontal distance dirs

4 结 论

本文提出利用智能反射表面能够操控电磁波环境、使无线通信信道变得灵活可控的特点，打破了将抗干扰通信研究重点全部放在收发机设计上的传统认识. 以无线信道唯一性、多样性等内生属性入手，从主动改变无线传输环境的观念出发，跳出了收发机被动适应信道的传统角度. 利用通信方先天具备的主动优势和先发优势，基于无线信道内生属性，构建动态捷变、空间异构和参数冗余的电磁传播环境.通过引入IRS 并智能调整其相移，提升系统抗干扰性能和能效. 具体来说，在给定接收SINR 的限制下，联合最优化发射机波束成形和IRS 相移以最小化系统发射功率. 通过应用SDR 和交替优化技术，我们提出了有效算法以权衡系统性能和计算复杂度. 而且，针对实际中干扰机CSI 难以获取的问题，提出了低复杂度次优以提升实际系统的抗干扰性能. 仿真结果表明，与传统空域抗干扰系统相比，在各种场景下，所提算法都能显著提高无线网络可对抗的干扰功率和功率效率. 并且，我们还给出了部署IRS 的有用见解，从而为实际设计和实施提供了有用的指导.在接下来的研究中，我们还得考虑CSI 获取不准确以及多用户之间的互扰问题.