北极东北航道商船陀螺罗经航向误差修正算法*

吴建华 杜 威 王 辰 付 鹏 聂根政 江心博

（1.武汉理工大学航运学院 武汉 430063；2.武汉理工大学内河航运技术湖北省重点实验室 武汉 430063；3.交通运输部规划研究院 北京 100020）

0 引 言

随着北极东北航道实现季节性通航[1]，商船急需能够满足极地水域航行需要的导航指向设备。传统磁罗经会受到磁场分布的影响，使其几乎无法在北极东北航道为船舶提供航向[2]，随着纬度升高，陀螺罗经会出现较大指向误差；光纤罗经[3]在极区水域使用精度好，然而由于成本高，尚未在商船上普遍使用；GPS卫星罗经价格低、精度高和备机时间短，但缺点是GPS信号可能会受到外界干扰[4]，造成卫星罗经不能正常工作。

陀螺罗经在实际使用过程中，航向误差与纬度、速度以及稳定性能等因素有关[5]。在提高陀螺罗经稳定性能方面，袁群哲等[6]根据陀螺罗经力矩方程和主轴运动方程，仿真研究了纬度、速度等与陀螺罗经性能指标的关系，提出提高陀螺罗经稳定时间的方法，但并未考虑极区高纬度对陀螺罗经稳定性能的影响；在此基础上，周红进等[7]仿真研究了在极区纬度下，静基座和动基座2个方面启动对陀螺罗经在极区稳定性能的影响，提出在极区合适纬度启动罗经能提高陀螺罗经稳定性。

在航向效应补偿方面，施闻明等[8]归纳了陀螺罗经航向效应，在陀螺仪三轴角速度输出的基础上，对航向效应进行了标定与补偿来处理陀螺罗经航向，提高了陀螺罗经的航向精度；在此基础上，廉璞等[9]分析了陀螺航向误差的传播机理，通过陀螺罗经航向效应与陀螺漂移之间的映射关系解算出漂移误差，实现陀螺罗经标定。夏卫星等[10]利用最小二乘法对船舶在匀转向过程中产生的航向误差建立了补偿模型用于误差修正，但并未考虑船舶在普通转向情况下航向变化误差补偿。

以 “吉非替尼”、“间质性肺病”、“间质性肺炎”为关键词进行检索CNKI、VIP及万方数据库，以“gefitinib”、 “interstitial lung disease”、 “interstitial pneumonia”为英文关键词检索PubMed数据库。检索时间为2002年7月～2018年5月。

在陀螺罗经回路控制和对准方面，陈建国等[11-12]研究了电控陀螺罗经的控制回路原理，提出变传递系数阻尼方法和可变修正回路传递系数方法用于中低纬度电罗经的航向修正。Liu等[13]引入方位轴旋转调制、缩短陀螺旋转周期和重新设计的罗经参数，以消除或减轻由旋转引起的罗经回路中低频传感器误差，提高了罗经对准精度。Xu等[14]采用数据重复计算算法，缩短了参数变化引起的对准时间延长，快速有效地实现动基座下的罗经对准；在此基础上，Wei等[15]仿真实现了大方位角偏差下陀螺罗经快速、准确地对准。

综上所述，针对陀螺罗经的相关研究大多围绕稳定性能、航向效应误差补偿以及陀螺罗经对准[16]展开，已有的研究成果主要体现在从陀螺罗经内部原理仿真分析、捷联惯导罗经航向对准以及罗经内部回路控制研究等方面来提高罗经航向精度，对利用高纬度航区如北极航道内陀螺罗经真实数据来对罗经航向误差进行拟合修正分析的研究较少。

贵州观赏石资源受控于省内三大岩性、地貌单元和两大地表水系。这三大岩性、地貌单元是：以碳酸盐岩类为主的喀斯特地貌单元，主要分布于贵州西部、南部和中部，面积约11万平方公里；以红色砂岩和页岩为主的丹霞地貌单元，主要分布于贵州北部地区，面积约1万多平方公里；以元古代浅变质岩为主的苗岭地貌单元，主要分布于贵州东部地区，面积约5万平方公里。

因此，随着北极航行常态化的进行，为保障船舶在高纬度下获得高精度陀螺罗经航向，本文将结合陀螺罗经的普适性和GPS卫星罗经高精度及低成本优势，利用“永盛”轮北极航行时采集的陀螺罗经、GPS卫星罗经历史数据，从纬度、航向，以及纬度与航向3个影响因素出发，采用最小二乘法开发并遴选出适用于北极东北航道商船的陀螺罗经/GPS卫星罗经误差拟合模型对陀螺罗经进行一次修正；基于GPS卫星罗经对一次修正后的航向采用卡尔曼滤波进行二次修正，以期为航行北极东北航道船舶驾驶人员提供高精度、高可靠性的船舶导航技术支持。

1 GPS卫星罗经航向解算模型

GPS罗经提供的航向精度与纬度无关，只与GPS接收的信号有关[17]。GPS卫星罗经是通过主、从GPS接收机接收卫星电波信息，提取卫星的位置和伪距、相位参数，比较卫星到2台GPS接收机的距离差，利用三者之间几何关系解算出船舶航向。

1.1 航向解算几何模型构建

依据GPS卫星与主、从天线之间的距离差，考虑主、从天线基线在站心坐标系中的几何关系建立方程，构建航向解算模型。

生态、低碳、环保是时代发展的潮流，也是档案保护发展的必然趋势。档案馆建筑群体及设备设施应遵循绿色环保的观念，最大限度地节约资源、保护环境、减少污染，提供健康、适用和高效的使用空间，与自然和谐共生。档案的保护方式以前是追求快速建造，现如今在逐渐向高效建造发展，更注重生态保护、低毒、无残留，从实质上迎合国家开展的绿色环保政策，从而保证档案馆的合理化建设。

站心坐标系见图1，以主天线位置O′为坐标原点(0,0,0)，从天线位置O′的坐标点为(X,Y,0)，X，Y未知待求，r为基线O′O′的长度（已知）。

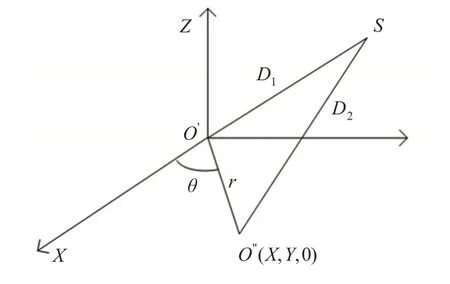
图1 主、从天线基线在站心坐标系中的几何关系Fig.1 Master and slave antenna baseline geometric elationships in the topocentric-coordinate system

Z轴与O′点的椭球法线相重合，X轴垂直于Z轴指向椭球的短轴即指向地理真北，而Y轴垂直于XO′Z平面指向地理东。只要计算出主从天线基线O′O′与X之间的夹角θ，就可以解算出卫星罗经航向。

设(Xh,Yh,Zh)为GPS卫星S在站心坐标系中的位置，则GPS卫星S到主天线O′的距离为

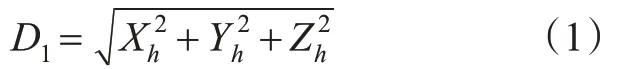
北极东北航道陀螺罗经航向一次修正算法的原理见图3。首先利用纬度、陀螺罗经航向和GPS卫星罗经航向的历史数据拟合GPS卫星罗经与陀螺罗经航向在北极东北航道高纬度航线的航向误差δψ，并得到拟合方程；然后测定航行船舶陀螺罗经航向值ψe及船舶纬度φ，代入拟合方程得到陀螺罗经拟合航向值ψe′；当GPS信号受到干扰，卫星罗经航向信息无法更新时，将直接输出陀螺罗经拟合航向值ψe′。

卫星与主从天线之间的距离差为

基线长度与从天线位置坐标关系为

联立式（1）～（4），建立卫星与主、从天线之间距离差方程。如果能求出ΔD，则可以得到X和Y的解，进而求出主、从天线构成的基线与地理真北之间的角度。

1.2 卫星与主、从天线的距离差

通过接收GPS卫星星历表可以计算出卫星在地心直角坐标系中的位置(XG,YG,ZG)，接收主、从天线位置的经纬度数据可以分别转换为地心直角坐标系中的位置，得到主天线O′（基准天线）在地心直角坐标系下的坐标为(X1,Y1,Z1)；从天线O′′在地心直角坐标系中的坐标为(X2,Y2,Z2)。因此，在地心直角坐标系中卫星到主天线的距离为

卫星到从天线的距离为

卫星与主、从天线之间的距离差为

1.3 航向解算

根据式（7）空间位置解析得到的GPS卫星与主、从天线之间的距离差ΔD和基线长度r求解基线方位θ，定义中间量为

当下,各类高端检测仪在临床检验领域有广泛应用,所以临床检验基本上都是仪器检测,因此尿干化学分析仪和尿沉渣分析仪是目前常用的现代化检验仪器。但如果要单项对比对红细胞的检测,在实际工作中的检测结果显示,尿干化学分析以比光学显微镜检测的阳性率更高,所以光学显微镜镜检可作为尿液红细胞检测的一个参考标准[10];对于尿中溶解的红细胞,光学镜检不能检测出,尿干化学分析仪可检测;尿沉渣分析仪的检测对尿红细胞的定量分析具有意义,但易受干扰影响,所以要用光学显微镜确认。

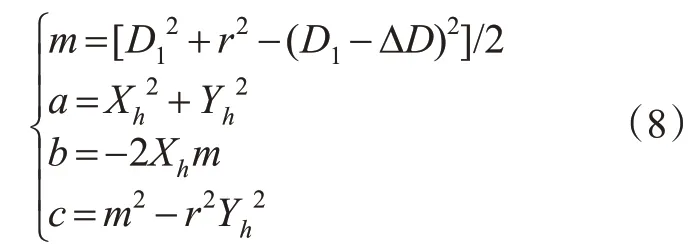
如果b2-4ac＜0，无解；如果b2-4ac＞0，则

对上述项目之外，现阶段无法预料的其他费用，按不包括固定资产折旧和利息净支出之外的其他各项费用之和的5%计算，按除折旧和利息净支出。

1.4 GPS卫星罗经航向精度分析

为了检验前述GPS卫星罗经航向解算模型的解算精度，通过实验采集提取主天线的#GPSEPHEMA、#BESTPOSA语句信息，从天线#MATCHEDPOSHA语句信息以及经过信号处理器解析的#HEADINGA语句信息，分别代入GPS卫星航向解算模型，计算出本船的解算航向，与本船的真航向即#HEADINGA语句中的基线方位进行比对，由此测算出GPS卫星罗经航向解算模型的解算精度。

向GPS航向解算模型输入基线长度为1.175 7 m，代入GPS卫星罗经航向解算模型运行程序得到解算航向，由真航向减去解算航向得到解算误差。解算航向及解算精度见图2。

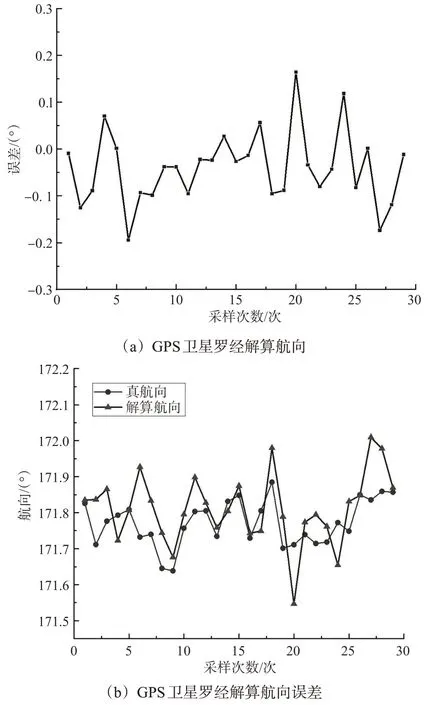
图2 GPS卫星罗经解算航向及精度误差Fig.2 Calculated GPS-satellite compass heading and accuracy error

为了分析纬度拟合模型的理论精度，将测试集纬度数据代入式（11）～（12）得到陀螺罗经拟合航向差值，又根据对应的卫星罗经航向数据比对出陀螺罗经拟合航向的精度，以此分析纬度拟合模型的理论精度。残差在数理统计中是指实际观察值与估计值（拟合值）之间的差，船舶实际航向（真航向）为卫星罗经航向，陀螺罗经拟合航向是船舶航向的拟合值，因此卫星罗经与陀螺罗经拟合航向的差值等于拟合航向残差值，以陀螺罗经拟合航向残差图表示纬度拟合模型的理论精度，分别见图6（a）～（b）。

聚束钻井液体系由聚束剂HMP、聚合物降滤失剂组成HFL-2、抑制剂胺基硅醇HAS和有机铝HOA-2、封堵剂HBJ-3、温压成膜封堵剂HCM、高效润滑剂HLB组成。高分子聚合物胶束分子中的疏水基团以类似表面活性剂憎水基团相互聚集形成胶束方式，相互聚集成疏水微区，导致分子内和分子间缔合，分子内缔合可增加分子刚性，而分子间缔合则可形成连续的网状结构，因为这种分子在水溶液中由静电、氢键或范德华力作用而在分子间产生具有一定强度但又可逆的物理缔合，形成巨大的三维网状结构。聚束钻井液以无毒、可生物降解的天然材料改性为主，具有较好的环保特性[4]。

2 GPS卫星罗经/陀螺罗经拟合修正

基于前述GPS卫星罗经航向精度与地理位置无关的结论，将GPS卫星罗经航向值作为标准值，利用北极航道历史数据得到卫星罗经与陀螺罗经航向的差值，即陀螺罗经在北极航道的航向误差。利用最小二乘法依次分析在纬度、航向以及纬度与航向影响下，对航向误差进行拟合，建立拟合方程，用拟合航向误差值对陀螺罗经输出航向进行修正，即为陀螺罗经修正后的航向，提高陀螺罗经的航向精度，保障北极航道船舶使用高精度、高可靠性的航向。

2.1 误差拟合原理

卫星到从天线O′的距离为

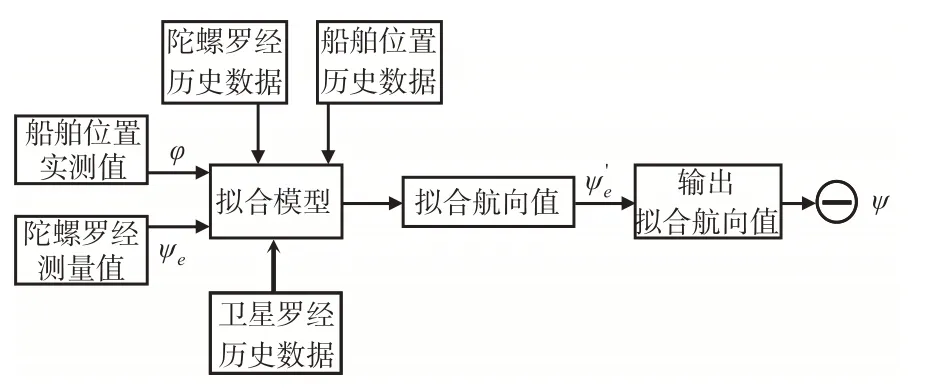
图3 北极东北航道陀螺罗经航向一次修正Fig.3 Firstly correction of gyrocompass in the Northeast Passage of theArctic

2.2 基于纬度影响的误差拟合

因纬度增加和纬度降低，陀螺罗经与GPS卫星罗经差值变化较大，对“永盛”轮2015年航行北极东北航道高纬度航线（北纬60°以上）的航行数据按从低纬往高纬航行和高纬向低纬航行分为2组，同时对每组数据进行划分，75%用作数据拟合，25%用作精度分析。以陀螺罗经与GPS卫星罗经航向差为拟合对象，航行纬度作为影响因子自变量，采用最小二乘法曲线拟合探究陀螺罗经与卫星罗经航向差和纬度之间的关系。

导入采样点pi(φi,δψi)，其中i=1,2,…,n，φi采样点纬度值，δψi为采样点陀螺罗经与卫星罗经航向差值，求近似曲线δψ=g(φ)，并使得近似曲线δψ=g(φ)与采样点的偏差平方和最小，近似曲线在点pi处的偏差为δi=g(φi)-δψi，i=1,2,…,n，偏差平方和为

北斗卫星导航系统是中国自行研发的全球卫星导航系统。可在全球范围内全天候、全天时为各类用户提供高精度、高可靠定位、导航、授时服务， 定位精度10m，测速精度0.2m/s，授时精度10纳秒。北斗卫星导航系统还具有短报文通信能力，用户可以一次传送40个～60个汉字的短报文信息，这是GPS等其他卫星定位系统所不具备的。

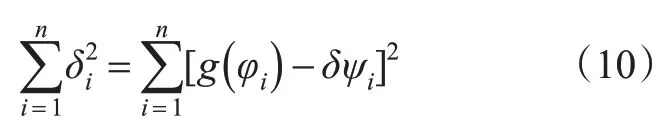
使偏差平方和达到最小即为最小二乘法曲线拟合[18]。并使用多项式函数，调整多项式的最高次幂，多次拟合遴选出残差较小的拟合模型，分组后的误差拟合曲线参见图4～5。

七年前，岳无影刚当上青城派掌门，出战皖南黑星寨，率人一口气杀了黑星寨上上下下几百人，直到剩下最后一个孕妇。

图4 纬度增加时误差拟合曲线Fig.4 Fitting curves of the errors with the increased latitude

图5 纬度减小时误差拟合曲线Fig.5 Fitting curves of the errors with the reduced latitude

2条曲线均为一元二次方程，低纬往高纬航行时GPS卫星罗经与陀螺罗经差值的拟合曲线方程见式（11）。

最终得到GPS卫星罗经航向θ。

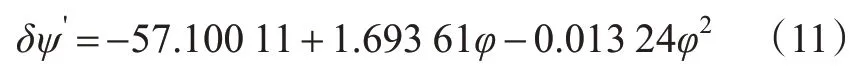
式中：x为纬度，（°）；y为陀螺罗经航向，（°）；f(x,y)为卫星罗经与陀螺罗经拟合航向差，（°）。

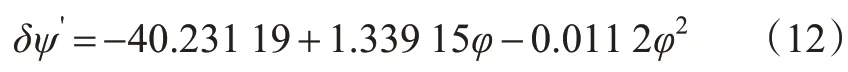
式中：δψ′为卫星罗经与陀螺罗经拟合航向差，（°）。根据实际航行过程，将纬度数据代入方程式（11）或（12）中，计算得到卫星罗经与陀螺罗经拟合航向差值δψ′，并根据陀螺罗经航向值ψe求取陀螺罗经拟合航向值ψe′，见式（13）。

由图2可知：解算误差较小，误差保持在±0.2°以内，精度较高，可以用GPS卫星罗经作为船舶真航向用于陀螺罗经的航向修正。

由图6可知：排除个别偶然误差较大的点，当纬度增加时陀螺罗经拟合航向残差保持在±3°以内，其中79%保持在±1°以内；纬度降低时陀螺罗经拟合航向残差保持在±2°以内，其中95%保持在±1°以内。纬度拟合模型对陀螺罗经航向具有一定的修正作用。

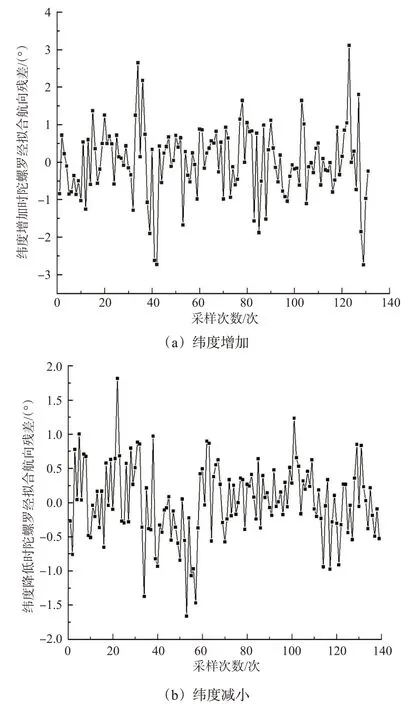
图6 陀螺罗经纬度拟合模型残差Fig.6 Residual error of the latitude fitting model of the gyrocompass

2.3 基于航向影响的误差拟合

同理以GPS卫星罗经与陀螺罗经航向差为拟合对象，采样数据点的陀螺罗经航向作为影响因子自变量，利用最小二乘法拟合的方法研究陀螺罗经与卫星罗经与航向差和陀螺罗经航向之间存在的数值关系。

令样本点为(ψei,δψi)。其中i=1,2,…,n，ψei为样本点陀螺罗经航向值，δψi为样本点卫星罗经与陀螺罗经航向差值，设拟合曲线为三次函数，

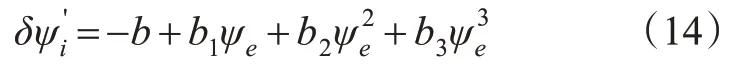
式中：δψ′

i为卫星罗经与陀螺罗经拟合航向差，（°）；b，b1，b2，b3为函数系数。

误差平方和为

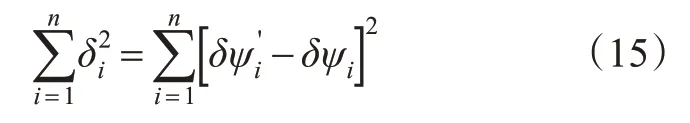
按照上述原理进行编程，使误差平方和最小，运行计算后可得到函数系数b，b1，b2，b3的值，并绘制出拟合曲线图见图7。

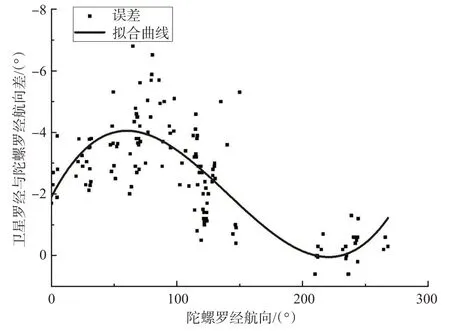
图7 基于航向拟合曲线图Fig.7 Fitting curves based on heading

拟合函数为

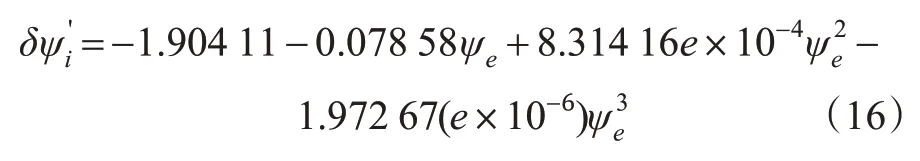
将训练集数据导入式（16），计算得拟合误差，以陀螺罗经拟合航向残差描述航向拟合模型的理论精度，见图8。可知：残差保持在±4°以内，其中67%保持在±1°以内，93%保持在±2°以内，基于陀螺罗经航向影响的拟合模型对比纬度拟合模型的理论精度要低。

图8 陀螺罗经航向拟合模型残差图Fig.8 Residual error of the heading fitting model of the gyrocompass

2.4 纬度和航向影响下的误差拟合

单独依据纬度数据来拟合GPS卫星罗经与陀螺罗经的航向差，其拟合函数得到拟合航向的精度基本在±3°以内；而单独依据陀螺罗经航向数据来拟合GPS卫星罗经与陀螺罗经的航向差，其拟合函数得到拟合航向的精度基本在±4°以内，以上2种拟合模型都能够在一定程度上修正陀螺罗经在北极东北航道高纬度航线产生的指向误差，提高航向测量的精度，但误差仍然较大。现综合考虑船舶航行时的纬度和航向，把地理纬度、陀螺罗经航向当作2个自变量对卫星罗经与陀螺罗经的航向差进行拟合，以期更近一步修正陀螺罗经产生的指向误差。

设采样点数据(xi,yi,zi),i=1,2,…,n，xi为纬度，yi为陀螺罗经航向，zi为陀螺罗经与卫星罗经航向差，需要在给定的函数类f上根据这些离散数据做出逼近曲面z=f(x,y)。

对于给定1个含参数c1,c2,…,cm的函数表达式z=f(x,y)和1组数据采样点(xi,yi,zi),i=1,2,…,n，需要求出表达式z=f(x,y)的参数。

首先，构造函数，见式（17）。

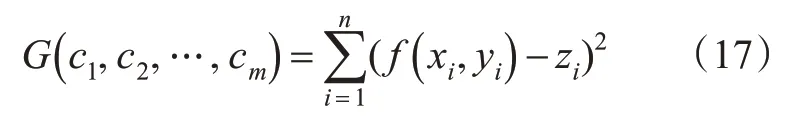
然后，根据最小二乘法的原理，要使函数G达到最小。利用数学分析的方法，G对cj,j=1,2,…,m求偏导数，得到m个方程。

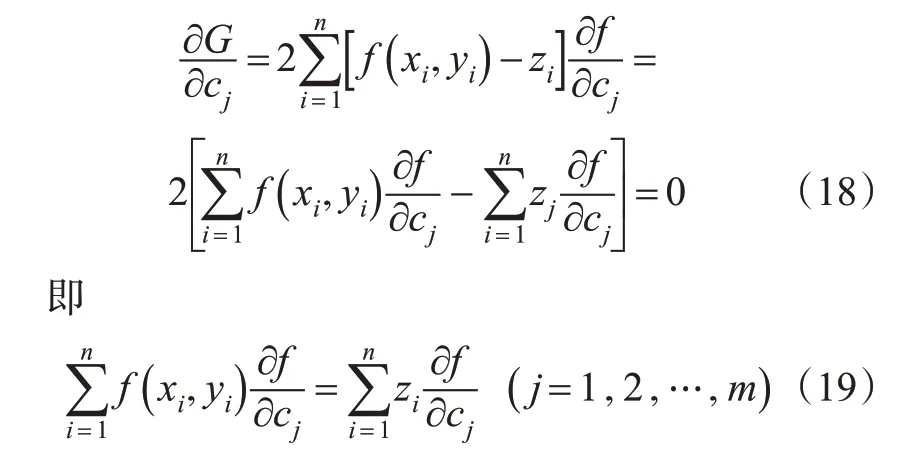
基于纬度、航向以及同时考虑纬度和航向的3种拟合，还不能判定哪种拟合模型的精度最高，引入计算卫星罗经与陀螺罗经拟合航向之间的均方根误差，均方根误差数值越小说明偏差越小，数学拟合模型的理论准确度越高，均方根误差计算公式为

拟合函数见式（20）。

高纬往低纬航行时GPS卫星罗经与陀螺罗经差值的拟合曲线方程见式（12）。

绘制的拟合曲面见图9。分析可知：当北极东北航道高纬度航线的航行船舶航向保持不变时，陀螺罗经航向误差随着纬度升高而逐渐增大；又当航行船舶位置保持不变时，船首方位越接近真北方位0°或360°，航向误差有增大的趋势。

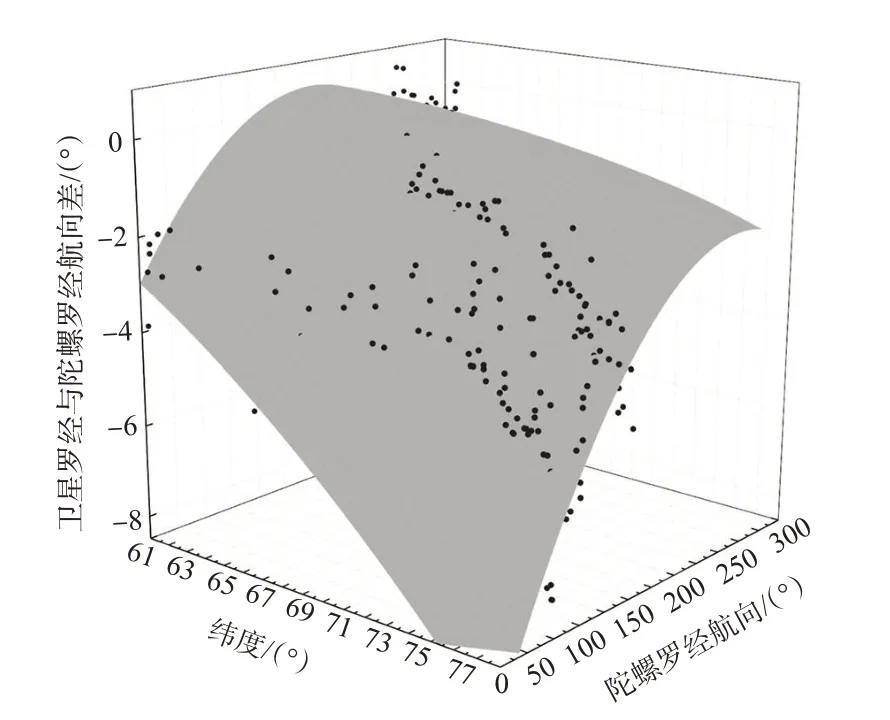
图9 纬度与航向合成拟合曲面图Fig.9 Synthetic fitting surface based on latitude and heading

为了研究纬度与航向合成拟合模型的理论误差，将测试数据代入模型，计算残差见图10。

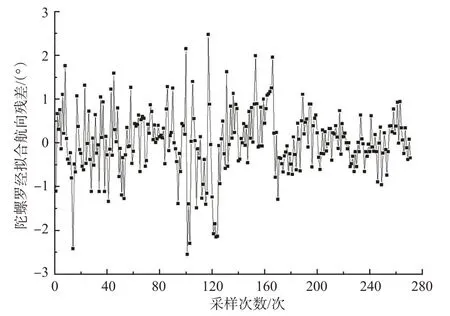
图10 陀螺罗经纬度与航向合成拟合模型残差图Fig.10 Residual error of the synthetic fitting model based on latitude and heading of the gyrocompass

由图10可知：陀螺罗经拟合航向残差保持在±2.5°以内，其中83%保持在±1°以内，同时经该拟合数学模型修正输出的陀螺罗经拟合航向值比较平滑，所以陀螺罗经纬度与航向合成拟合模型与样本数据具有较好的拟合度。

根据私募通发布的一份数据显示，2016年1～11月，中国并购市场共完成交易2904起，披露金额的并购案例总计2256起，共涉及交易金额13392.16亿元，同比上升37.19%，平均并购金额为5.94亿元。其中物流企业并购案例41起，并购金额达519.56亿元。另一组数据则显示，2006年至2014年间，中国物流企业共发生收购并购664起。笔者虽然没有找到2017年的确切数字，但是从物流行业的相关协会那里得知，这两年物流行业的并购案例以及并购金额比往年只多不少。

3 拟合模型适应性分析

3.1 拟合模型理论精度分析

最后，利用牛顿法求解这个非线性方程组，得到参数c1,c2,…,cm的解，这样便完成了曲面函数z=f(x,y)的拟合。

式中：ψGPS为卫星罗经航向；ψe′为陀螺罗经拟合航向。将所有拟合数据代入式（21）计算3种拟合结果的均方根误差，见表1。

表1 拟合模型理论均方根误差统计表Tab.1 Theoretical root-mean-square error statistics of the fitted model

计算得卫星罗经与陀螺罗经原始数据的均方根误差为3.404 890 251。由表1可知：各类拟合模型的均方根误差都较小，拟合的总体偏差最大的是航向拟合模型，偏差最小的为纬度与航向合成拟合模型，其总体偏差小于0.8°，与原始数据相比具有较好的修正效果。分析可知：纬度与航向合成拟合模型理论精度较高且较为平滑，该模型对北极东北航道高纬度航线航行船舶陀螺罗经的误差修正具有一定的参考价值。

3.2 拟合模型应用适应性分析

为了评价陀螺罗经航向误差拟合模型的实用性，本文以划分的25%测试集陀螺罗经航向数据、纬度数据和卫星罗经航向数据依次输入上述3类拟合模型，得出陀螺罗经拟合航向值，然后计算卫星罗经与陀螺罗经拟合航向差，即为拟合模型的应用精度，统计数据并绘制拟合模型应用精度比对见图11。以期验证拟合模型的适用性并遴选出总体偏差最小的数学拟合模型，作为修正北极东北航道高纬度航线陀螺罗经较大指向误差的方法。

图11 拟合模型应用精度比对图Fig.11 Comparison of the fitting model's application accuracy

分析可知：纬度拟合模型的应用精度基本保持在±3°以内；纬度与航向合成拟合模型的应用精度基本保持在±2°以内，航向拟合模型的应用精度较差一些，达到±4°。通过计算拟合模型的均方根误差来判断其总体偏差，结果见表2。

2）处理倍数。3月1日开始用国光大果进行处理的，每10 mL对水4.3 kg；3月2日下午开始用吡效隆加强型进行处理的，每10 mL对水8 kg。

表2 拟合模型应用精度均方根误差Tab.2 Root-mean-square error of the applied accuracy of the fitted model

由表2可知：纬度与航向合成拟合的总体偏差最小为0.70°。综合考虑，航向拟合模型的应用精度较高，纬度拟合模型次之，纬度与航向合成拟合模型的应用精度最高，说明该模型的适用性最好，因此遴选出纬度与航向合成拟合模型修正陀螺罗经实测航向，作为航向融合算法的一次修正。

4 基于卡尔曼滤波的二次修正

尽管利用GPS卫星罗经航向与陀螺罗经航向之差拟合的方法对高纬度环境下陀螺罗经航向误差有较大幅度的修正作用，但是离陀螺罗经在普通纬度使用时的航向精度还有一定的差距。因此，这里提出当GPS卫星罗经工作正常时，采取对陀螺罗经航向实施二次修正以期进一步提高指向精度的方法，即利用基于实时测量的GPS卫星罗经航向将一次修正后的陀螺罗经拟合航向值用卡尔曼滤波进行二次修正，得到陀螺罗经二次修正后的滤波航向。GPS卫星罗经与二次修正后的滤波航向的差值即为陀螺罗经二次修正后的精度。

当GPS正常时，可以对陀螺罗经航向实施二次修正；当GPS异常时也可以对陀螺罗经航向实施一次修正，提高陀螺罗经的航向精度，保障北极航道船舶使用高精度、高可靠性航向。基于卡尔曼滤波的GPS卫星/陀螺罗经航向二次修正的方法见图12。

随着国内葡萄酒行业、侍酒师行业的发展，越来越多人像他们那样，一边工作，一边考试升级，不断努力，只为让自己更专业。正如戴鸿靖所说：“这个时代给予了无限可能。距离很多东西其实都很近，比如距离Michelle Rolland只相隔了一个人，近距离观察Rolland怎么做调配也不远。所以有梦想，去做，身边所有人都会帮你的。”

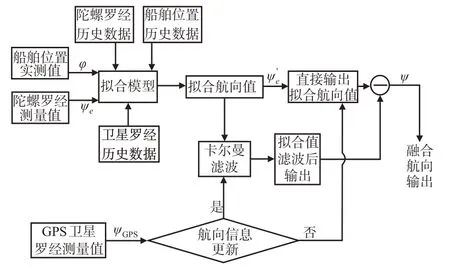
图12 基于卡尔曼滤波的陀螺罗经/GPS卫星罗经航向二次修正Fig.12 Second correction of the heading of the gyrocompass/GPS satellite gyrocompass based on Kalman filter

4.1 卡尔曼滤波模型

卡尔曼滤波的基本思想[19]是：以K-1时刻的最优估计为准，预测K时刻的状态变量，同时又对该状态进行观测，得到观测变量Zk，再在预测与观测之间进行分析，或者说是以观测量对预测量进行修正，从而得到K时刻的估计量xk。

基于卡尔曼滤波的基本思想利用GPS卫星罗经航向测量值ψGPS去修正陀螺罗经拟合航向值ψ′e，从而输出滤波航向ψ。正常航行于北极东北航道航线的船舶是按计划航线航行的，所以在短暂的时间内可以认为K时刻的船舶实测航向与K-1时刻的实测航向相等，船舶航向也不是随时间连续变化的，而是离散的并没有误差更新迭代的过程，每个离散实测航向量都相互独立。

最后，苹果音乐和世界知名唱片公司(如环球音乐唱片公司和华纳兄弟唱片公司等)的长期战略合作保证了其音乐品质的高水准和音乐内容更新的及时性，并邀请美国多位知名艺人如Lady Gaga、Bruno Mars和Chance the Rapper作为Beats1访谈环节的常驻嘉宾，使节目的专业化水准大大提升。

具体的滤波方法为：当GPS信号正常时，可以采集到同时刻同地点的北极东北航道陀螺罗经航向测量值ψe和GPS卫星罗经航向测量值ψGPS，因受到高纬度环境的影响，陀螺罗经航向误差δψ较大无法满足船舶指向需求，因而采用遴选出的基于纬度和航向合成的拟合模型修正陀螺罗经航行值ψe，得到拟合航向值，作为陀螺罗经航向的预测值，将卫星罗经航向测量值ψGPS作为观测值Zk再去修正陀螺罗经航向预测值，最后将输出更高精度的滤波航向ψ作为航向估计量xk。

然后，得到航向估计量xk，见式（23）。

4.2 滤波结果

用Matlab编译卡尔曼滤波算法，将经过一次修正的陀螺罗经拟合航向数据和GPS卫星罗经观测航向ψGPS数据导入算法中，运行程序得到滤波航向ψ并保存。

为了说明北极东北航道高纬度环境下陀螺罗经/GPS卫星罗经航向融合算法的适用性，结合“永盛”轮航行试验数据绘制卫星罗经与陀螺罗经航向差、陀螺罗经一次修正后的误差以及陀螺罗经二次修正后的误差（即滤波航向）对比见图13。

广西工程建设地方标准《绿色建筑质量验收规范》（以下简称《验收规范》，DBJ/T45-068-2018）将于今年11月1日开始实施。这意味着广西开展绿色建筑工程质量验收工作将有据可依、有规可循。

图13 陀螺罗经航向误差修正对比图Fig.13 Comparison of the heading error-correction of the gyrocompass

分析可知：①当GPS信号异常时，航向修正算法可以通过数学拟合的方法进行一次修正陀螺罗经指向误差，一次修正后的陀螺罗经航向精度总体保持在±2°以内，其中航向精度在±1°以内的航向修正率为88.4%；②当GPS信号正常时，GPS卫星罗经/陀螺罗经航向修正算法可以对陀螺罗经进行二次修正，输出的滤波航向非常平滑且精度高，航向精度保持在±1.0°以内的航向修正率为98.9%；在±0.5°以内的航向修正率为88.9%。

5 结束语

本文基于北极东北航道卫星罗经和陀螺罗经历史数据，提出了1种利用最小二乘法考虑航向、纬度等影响因子分别对卫星罗经与陀螺罗经的航向误差进行拟合分析比较，最终建立基于纬度和航向共同影响的陀螺罗经误差修正模型。当GPS异常时，可通过该模型进行陀螺罗经航向一次修正，提高指向精度；当GPS正常时，可基于卫星罗经航向对一次修正值采用卡尔曼滤波进行二次修正，进一步提高指向精度。研究结果表明，修正模型能够修正北极东北航线上陀螺罗经的大部分误差，其中经过一次修正模型修正后航向精度在±1°以内的修正率高达88.4%，二次修正模型修正后修正率高达98.9%，能够明显提高北极东北航道商船陀螺罗经的指向精度。在未来的研究中，可进一步探索船舶在北极其他航道航行时陀螺罗经的误差修正算法。