面向智能网联汽车定位的协同地图匹配算法*

陈 伟 杜路遥 孔海洋 傅率智 郑洪江

（1.武汉理工大学自动化学院 武汉 430070；2.上海博泰悦臻电子设备制造有限公司 上海 200030；3.上海智能网联车载终端工程技术研究中心 上海 200000）

0 引 言

近年来，随着高精度地图和高精度定位技术的发展，协同地图匹配作为智能网联环境下低成本高精度的定位新方式得到越来越多的关注。该方式利用智能网联环境下车辆之间共享全球导航卫星系统（global navigation satellite system，GNSS）定位数据和道路约束信息，然后在地图匹配过程中应用联网车辆的道路约束条件，消除公共偏差，提高车辆定位精度[1]。协同定位思想最早由Karam等[2]提出，他们通过无线通信实现1组车辆状态信息的互换，然后利用扩展卡尔曼滤波（extended Kalman filter,EKF）进行数据融合实现车辆定位精度的提高。Yao等[3]对1种协议进行了改正，改进后的协议有效的解决了协同定位所需的大量状态信息交换时所增加的车辆网络分组碰撞率问题，也提高了协同定位的有效性。罗文慧等[4]基于扩展卡尔曼滤波融合车辆全球定位系统(global positioning system，GPS)和航位推算（dead reckoning，DR）数据得到交叉口车辆的初始定位，再结合地图协同匹配(cooperative map-matching，CMM)算法修正，提高了车辆定位精度。徐宏宇等[5]通过实测GPS数据验证了EKF算法，实验结果表明了该算法对于GPS的定位数据具有较好的过滤效果。Schubert等[6]提出利用道路约束条件实现协同定位和地图匹配，但是这种定位方式需要借助激光雷达等传感器获取车辆之间的相对位置，增加了算法的计算复杂度和设备成本，且还可能出现过度收敛问题。此后，Khaoula等[7]提出了1种协作的全分布式估计方法，该方法不会使估计过度收敛。而Efatmaneshnik等[8]提出了1种新车载网络定位算法，该算法融合地图匹配较大的减少了迭代次数和收敛时间。在此基础上，Alam等[9]提出了1种通过融合车辆伪距观测数据改进车辆定位结果的方式，使车辆定位精度得到提升，但是该方式仍然没有解决需要增加传感器的问题。Mohsen等[10]提出通过原始GNSS定位数据修正公共偏差，利用道路约束条件改进定位结果的方式。该方式不仅不需要额外增加传感器设备，还提高了车辆定位精度。Mohsen还使用了移动参考站来扩展DGPS的方法。该方法中，附近车辆生成的伪距以广播的形式传送给相邻近的车辆所接收使用。但此方法中由于移动的参考站不具有精确的已知位置，这使得由它们产生的伪距校正有着明显的不确定性。Liu等[11]提出了基于车间距检测的分布式位置估计算法，该算法的实现仅依赖于不够准确的全球定位系统的伪距测量和获得的车间距，而不用任何的参考点进行定位校正，但是也带来了定位的不确定性。Mohsen等[12]中提出了1种基于GPS数据与车距测量数据融合的分散贝叶斯协同车辆方法。该方法不仅提高了车辆定位精度，还讨论了这种方法对于降低定位不确定性、过度收敛问题的影响。殷鹏等[13]基于粒子匹配精度以及匹配效率的自适应调整方法，解决了在特定环境下机器人协同匹配的粒子退化及粒子收敛速度过慢的问题。为了定量评估道路约束对于CMM算法精度的影响，Shen等[14]提出了1项理论研究，为相关的评估提供了1个参考标准。此后，Shen等[15]提出了1种基于Rao-Blackwellized粒子滤波的协同地图匹配算法，该算法利用伪距误差模型计算公共偏差，能够进一步提高车辆定位精度。但是，通过算法仿真和分析可知，随着迭代次数和联网车辆数目的增加，地图匹配约束条件逐渐增强，算法出现“粒子耗尽”问题的概率有所提升。因此，Rao-Blackwellized粒子滤波只能在短时间内满足算法的一致性要求，而随着时间推移和联网车辆数目的增加可能无法持续满足这一要求。本文针对协同地图匹配算法中随着时间推移和联网车辆数目的增加容易出现的“粒子耗尽”问题，提出了1种基于自适应遗传Rao-Blackwellized粒子滤波（RBPF）的协同地图匹配算法，将自适应遗传步骤引入到粒子滤波的重采样过程中，以增加粒子的多样性，解决传统粒子滤波算法中容易出现的“粒子退化”和“粒子耗尽”问题，从而实现持续的高精度车辆定位。

1 算法研究

1.1 协同地图匹配算法原理

如图1所示，绿色圆点表示车辆实际位置，红色圆点表示GNSS接收机解算位置，红色椭圆表示接收机定位置信区域的误差椭圆。图1中所示车辆利用专用短距离通信（DSRC）技术实现互联，并按照图2内容共享自身GNSS定位原始数据（时间戳、伪距测量值），以及所处位置的地图数据信息（道路中心线及道路宽度）供目标车辆使用。

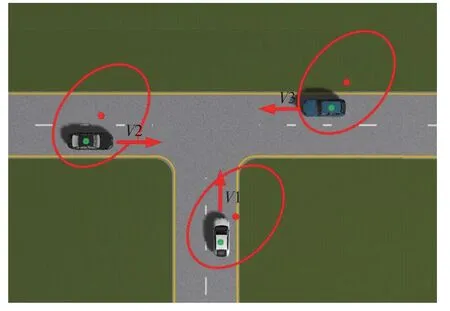
图1 典型协同地图匹配场景Fig.1 Typical scenario of the cooperative map

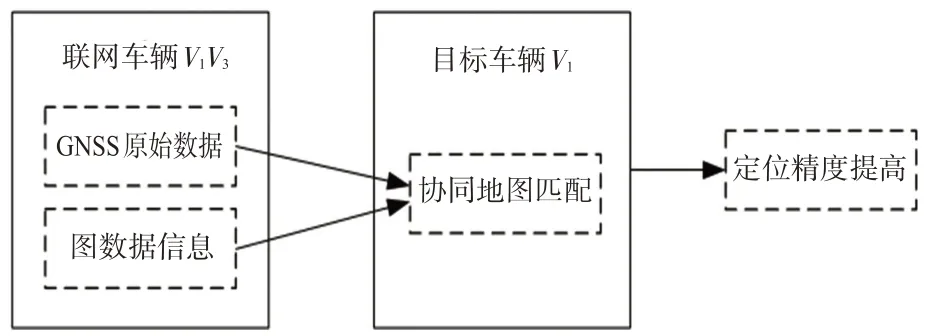
图2 网联数据链Fig.2 Datalink of the Internet of Vehicles

假设白色汽车V1为目标车辆，即该车使用协同地图匹配算法实现车辆的高精度定位，图3展示了典型协同地图匹配应用场景下联网车辆数目为3时目标车辆定位置信区域的变化过程。将GNSS接收机进行长时间静置，可以得到接收机北向误差的标准差σx、东向误差的标准差σy及协方差σxy，从而计算得到误差椭圆的置信区域。正常情况下车辆只能行驶在道路上，目标车辆首先利用自身道路约束条件可以将其定位误差区域缩小至图3（a）白色网状区域内；然后，利用黑色车辆V2共享的地图约束信息，误差区域可以缩小至图3（b）所示白色网状区域；最后，利用蓝色车辆V3的道路约束条件，可以将定位误差范围进一步缩小至图3（c）白色网状区域。

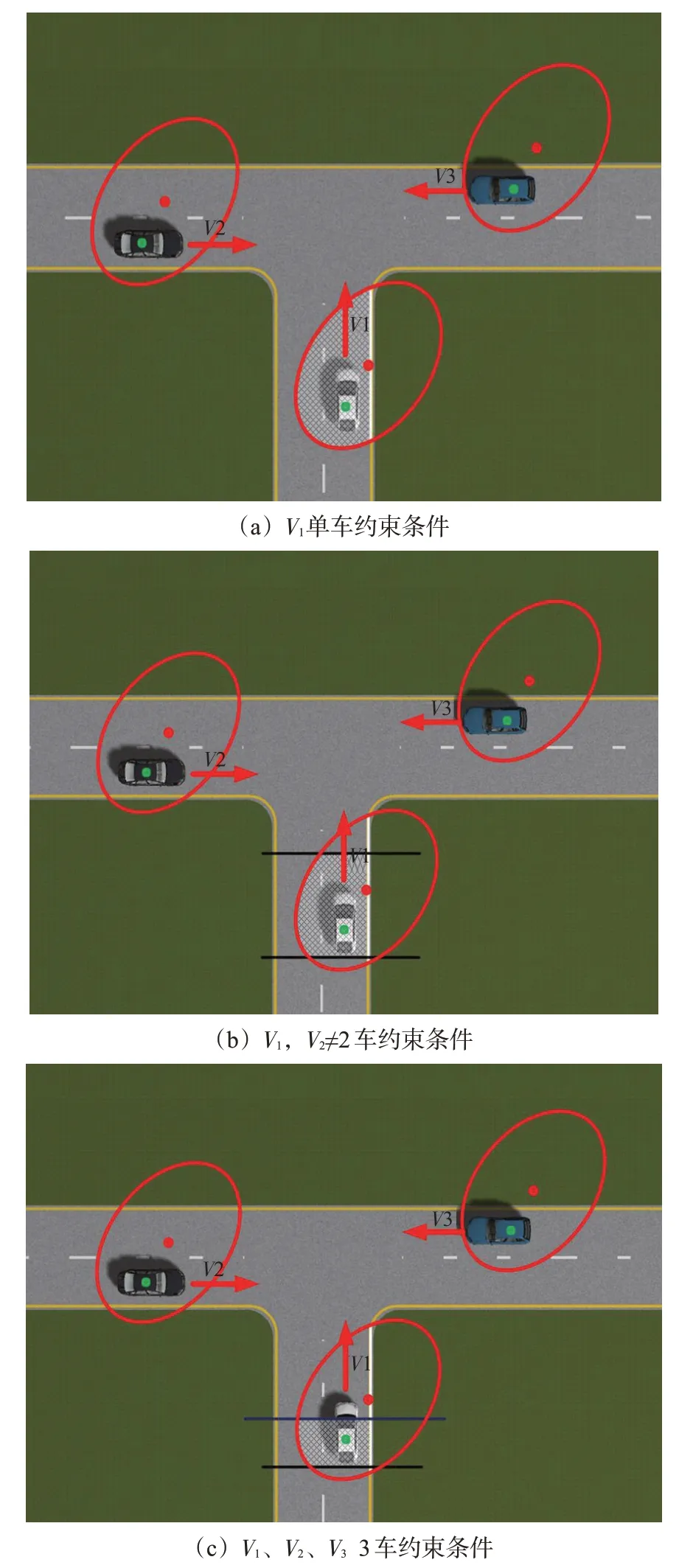
图3 对目标车辆使用道路约束条件Fig.3 Applying vehicles road constraints to the target vehicle

1.2 基于自适应遗传粒子滤波的协同地图匹配算法

为了增加粒子多样性，解决“粒子退化”和“粒子耗尽”问题，根据协同地图匹配算法基本原理，结合文献[6]中所提出的地图约束条件匹配方法及文献[15]中所提出的rao-blackwellized粒子滤波方法，并将自适应遗传步骤引入粒子滤波的重采样过程中，提出并建立基于自适应遗传粒子滤波的协同地图匹配方法，算法流程见图4。协同地图匹配算法执行步骤如下。

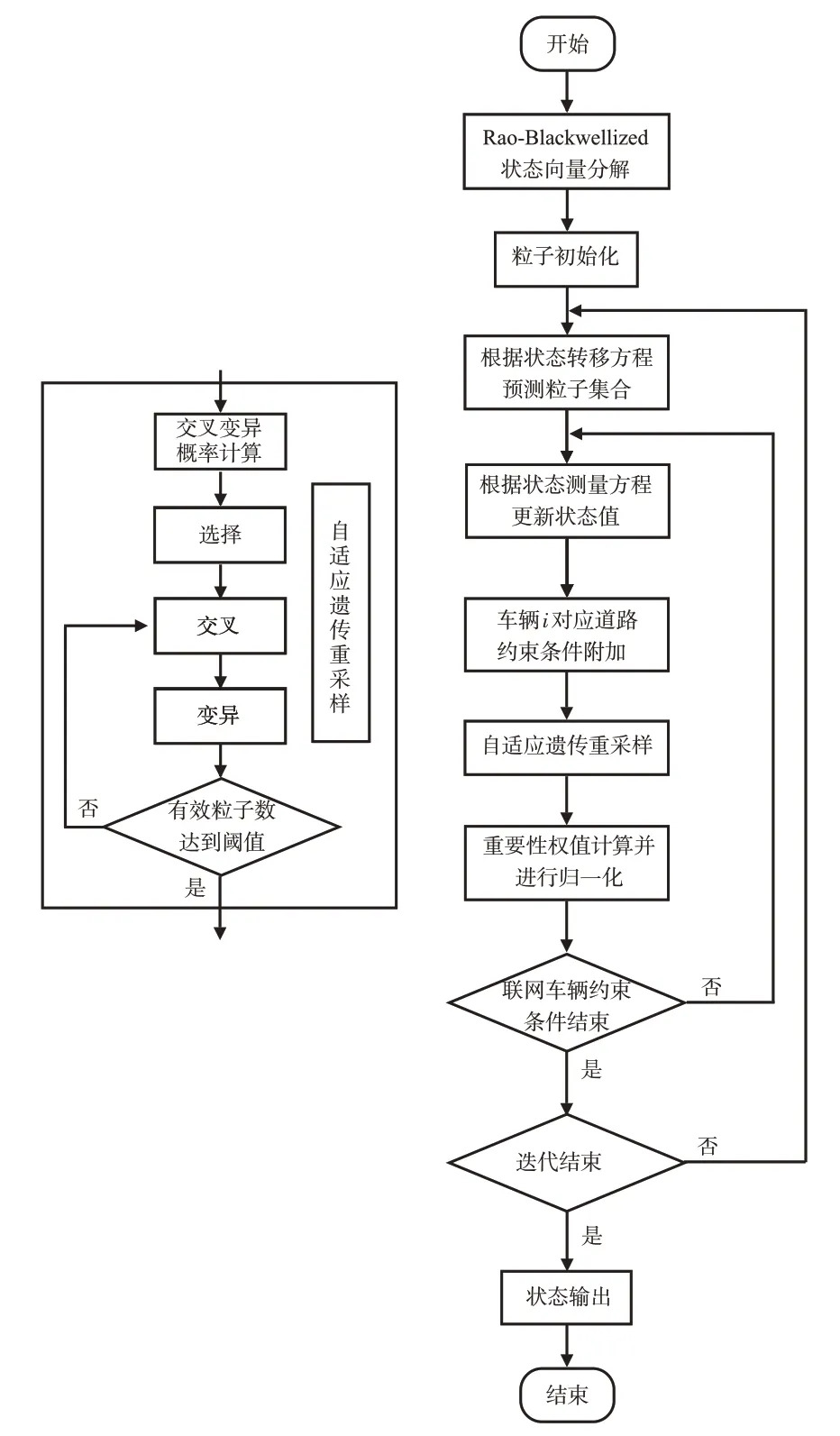
图4 算法执行步骤Fig.4 Steps of the algorithm

步骤1。粒子初始化，根据车辆状态以及公共偏差值初始化一群粒子。

步骤2。根据状态转移方程分别估计公共偏差状态和车辆状态值[3]。

步骤3。计算粒子权重并根据状态测量方程更新车辆状态和公共偏差状态值[3]。

步骤4。根据道路约束条件重新计算粒子权重[7]。

步骤5。自适应遗传重采样，包括选择、交叉、变异步骤。

1）选择操作。根据轮盘赌法在采样粒子集合中选择一定数目的粒子作为新的粒子集成员。

2）交叉操作。在新的粒子集合中随机选取2个粒子作为交叉父本进行交叉配对，得到的交叉概率pc进行交叉操作，经过交叉配对后得到的2个新个体分别为

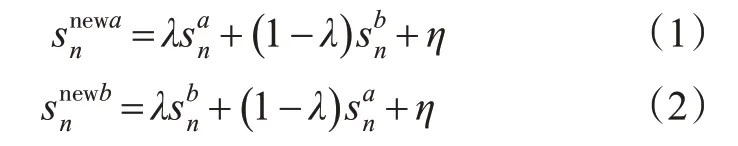
式中：λ:U[0,1]；η:N(0,∑)；U[0,1]为λ符合在[0,1]区间内的均匀分布；N(0,∑)为η符合均值为0，方差为∑的高斯分布。其中，λ为交叉配对产生的新粒子中保留对应父本粒子信息源的比例。

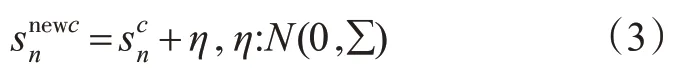
根据n时刻的状态观测值，计算粒子的适应度值以及交叉概率pc和变异概率pm。

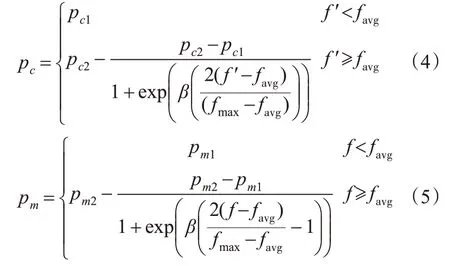
式中：favg为迭代过程中采样粒子集合的平均重要性权值；fmax为采样粒子集中最大的重要性权值；f′为粒子群体中需要进行交叉操作的2个粒子中较大的重要性权值；f为需要进行变异操作的粒子重要性权值；β为常数。

随机选择粒子进行交叉变异操作，根据Metropolis准则决定新粒子的去留，最后得到新的粒子集并进行权值归一化处理。即如果满足，则交叉得到的新粒子就会保留在新的粒子集合中，否则该粒子将以概率保留在新粒子集中。同理，对于新粒子将采取同样的方式决定其是否留在新的粒子集中。对于变异得到的新粒子，如果满足，则接收该粒子

步骤6返回至步骤3，直到针对所有联网车辆的道路约束条件应用结束。

步骤7返回至步骤2，直到算法迭代次数满足条件。

2 仿真分析

针对提出的基于自适应遗传RBPF的协同地图匹配算法模型进行仿真实现和结果分析。为更加客观地评价算法性能，仿真过程中引入传统粒子滤波和卡尔曼平滑粒子滤波方式进行对比；同时，为了验证算法的适应性，文章针对不同联网车辆数目下的定位结果进行比较和分析。

2.1 仿真环境搭建及参数设置

动态场景仿真实验平台为Prescan软件，同时结合Matlab R2019b实现算法仿真，为了更好的模拟GNSS定位中的公共偏差以及卫星数据，本文选择使用第三方提供的GPSoft Satellite Navigation工具箱作为车辆定位数据来源。该工具箱可以实现导航卫星、传播环境、接收机测量以及数据处理等卫星导航功能的模拟，利用开普勒参数对卫星星座进行仿真。仿真参数设置参见表1。其中：pc为交叉概率；pm为变异概率；β为常系数；Ns为可见卫星数量；Nv为联网车辆数目；n为迭代次数。公共偏差初始化过程中，在实际公共偏差的基础上增加方差为=0.25m2的白噪声。

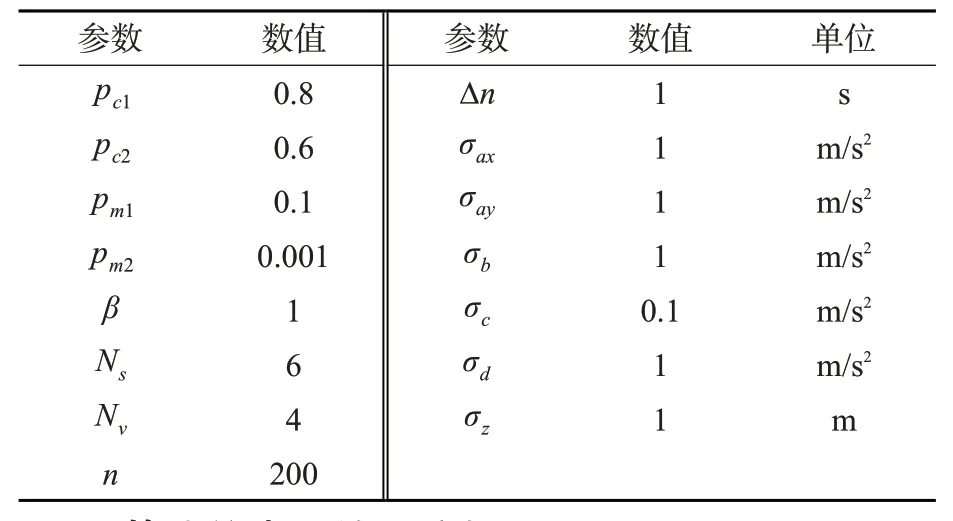
表1 仿真参数设置Tab.1 Values of simulation parameters

2.2 算法仿真及结果分析

为了分析算法定位效果，针对算法的定位结果进行了仿真研究和分析。仿真实验场景为正交十字路口，道路长1 200 m，车道宽度3.5 m，车辆宽度1.8 m，4台实验车辆均以10 m/s的速度沿车道中心线向十字路口作匀速直线运动并于路口右转弯，算法迭代次数n为200次。仿真过程中，GNSS接收机的原始水平定位误差均值为4.0 m，地图约束过程中对应的地图精度为1.0 m。

粒子数目Nm=100时，某次独立重复实验的仿真结果见图5。图5（a）展示了协同地图匹配在3种不同滤波算法下目标车辆V1的水平定位误差范数值；图5（b）展示了3种算法对应的协方差行列式范数值。

由图5（a）可知，对于GNSS接收机得到的原始定位数据直接使用静态粒子滤波方式进行协同地图匹配得到的定位效果最差。因为接收机得到的原始数据在不经过预处理直接参与地图匹配的情况下，其运算结果受到漂移和噪声的影响较为严重，很难得到较好的滤波效果；通过卡尔曼滤波将接收机数据平滑之后，可以有效滤除部分噪声，使定位结果有所改善；但是笔者提出的自适应遗传RBPF算法定位效果最好，水平定位误差明显小于其他2种算法。

由图5（b）可得，所提出的算法估计协方差行列式范数值和波动程度均明显小于其他2种算法，这得益于该算法符合贝叶斯估计模型。在估计过程中算法考虑到公共偏差随时间的变化，不仅将当前误差计算在内也将历史数据中的公共偏差考虑在内，而公式（2）进一步加强了公共偏差的时间相关性，使算法能够利用道路约束条件的叠加进行误差估计和消除。其他2种算法没有考虑公共偏差的时间相关性，直接将公共偏差与非公共偏差一并消除，导致算法估计不稳定，定位效果不理想。

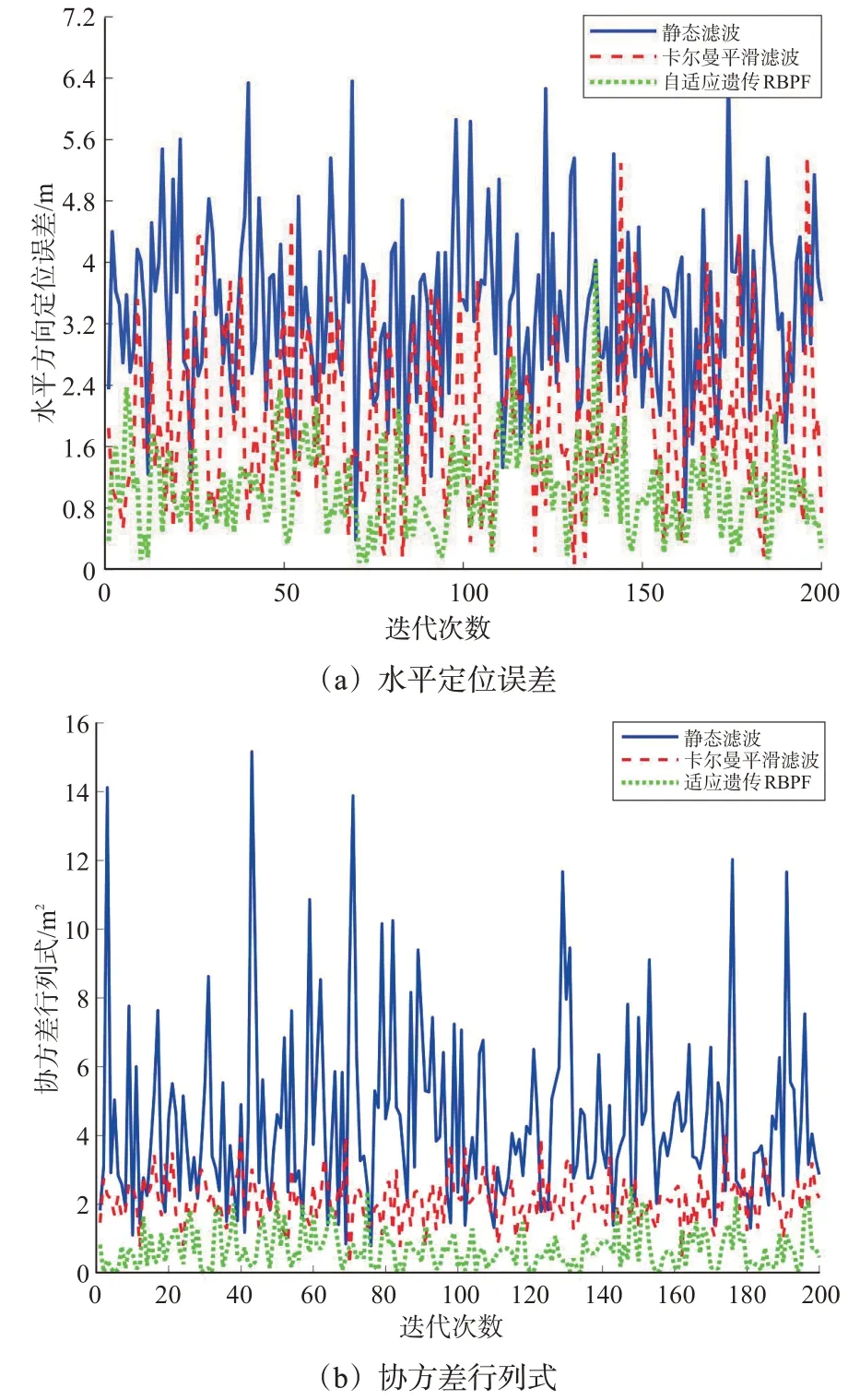
图5 3种不同算法对应仿真实验结果Fig.5 Simulation results of three different algorithms

为了更加客观地分析所提出的协同地图匹配算法性能，笔者通过50次蒙特卡洛独立重复实验统计3种算法对应的仿真结果，见表2。

从表2可见：随着粒子数目的增加，3种算法的水平定位误差均有所降低。在粒子数目相同的情况下，所提出的基于自适应遗传RBPF的协同地图匹配算法水平定位误差比静态粒子滤波和卡尔曼平滑粒子滤波更小。当粒子数目为200时，笔者提出的协同地图匹配算法的水平定位误差范围缩小至1.08 m。此外，通过3种算法平均耗时对比可以看出，在粒子数目较少的情况下，自适应遗传RBPF算法实时性相对较好，但是随着粒子数目增加，算法耗时与其他2种算法之间的差距逐渐增大。对于自适应遗传RBPF算法，粒子数目由50增加到200，其水平定位误差平均降低了0.38 m。即便在粒子数目相对较少的情况下，其定位结果受到的影响也不是特别大。因此，为了保证算法实时性，在实际工程应用中应选择相对较少的粒子。仿真结果表明：该算法的滤波性能以及定位效果均优于静态粒子滤波以及卡尔曼平滑粒子滤波，但是为了平衡算法实时性和定位精度需要选择较为合适的粒子数目进行滤波估计。

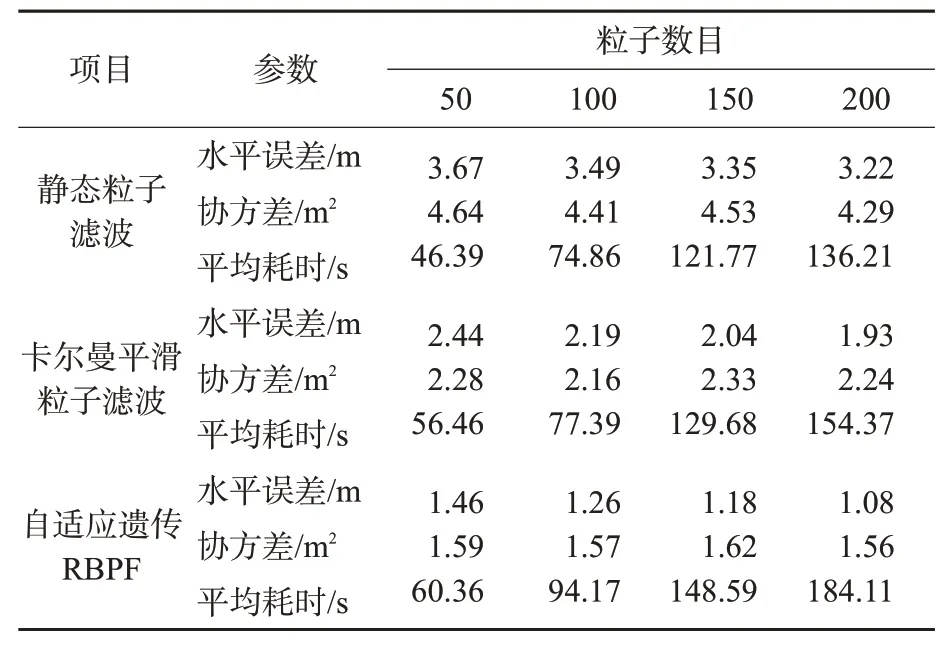
表2 50次蒙特卡洛实验定位结果均值Tab.2 Means of positioning result of 50 Monte Carlo experiments

为了验证算法的适应性，针对不同联网车辆数目情况下算法对车辆定位的影响进行了研究和分析，仿真实验场景为正交十字路口，见图6。图中车辆编号从V1到V10，箭头表示车辆运动方向，车辆以10 m/s的速度沿车道中心线做匀速直线运动，图中所示为算法仿真过程中某一时刻车辆所在位置，仿真条件和参数同表1，且精度一致。本文针对2～10辆不同联网车辆数目情况下，算法对定位精度的影响进行仿真实验。当联网车辆数目为2时，选择编号为V1、V2的2辆车运行；当联网车辆数目为3时，选择车辆编号为V1～V3的3辆车运行；联网车辆为4～10辆时以此类推；最终实现9种联网车辆数目情况下算法对车辆定位精度的影响。

图6 多车十字路口场景Fig.6 Scene of multi-vehicle intersection

为了客观地分析算法性能，通过50次独立重复的蒙特卡洛实验得到9种不同情况下的定位结果，实验统计分析结果见图7～9及表3。实验结果分别展示了算法的水平定位误差、公共偏差估计误差以及协方差行列式与联网车辆数目之间的关系。

表3 不同联网车辆数目下定位结果Tab.3 Positioning results under different numbers of connected vehicles

图7 水平定位误差与联网车辆数目之间的关系Fig.7 Relationship between horizontal position errors and the number of connected vehicles

图8 公共偏差与联网车辆数目之间的关系Fig.8 Relationship between the errors of common deviation and the number of connected vehicles

通过实验结果对比可以看出，在使用单车地图匹配方式可以大幅提高车辆定位精度的情况下，如果使用协同地图匹配算法进行定位，其定位误差会随着联网车辆数目的增加而减小，但是二者之间并非线性关系。这是因为随着道路约束条件的增加，车辆定位的误差范围逐渐减小，出现在道路外侧的粒子数目也会变少，此时约束条件对粒子无法起到约束作用。此外，从图9可看出，同水平定位误差以及公共偏差估计误差一样，图中所示粒子的协方差行列式也随着联网车辆数目的增加而有所降低。这表明随着联网车辆数目的增加，估计位置的不确定性在减小，算法估计的准确度有所提高。

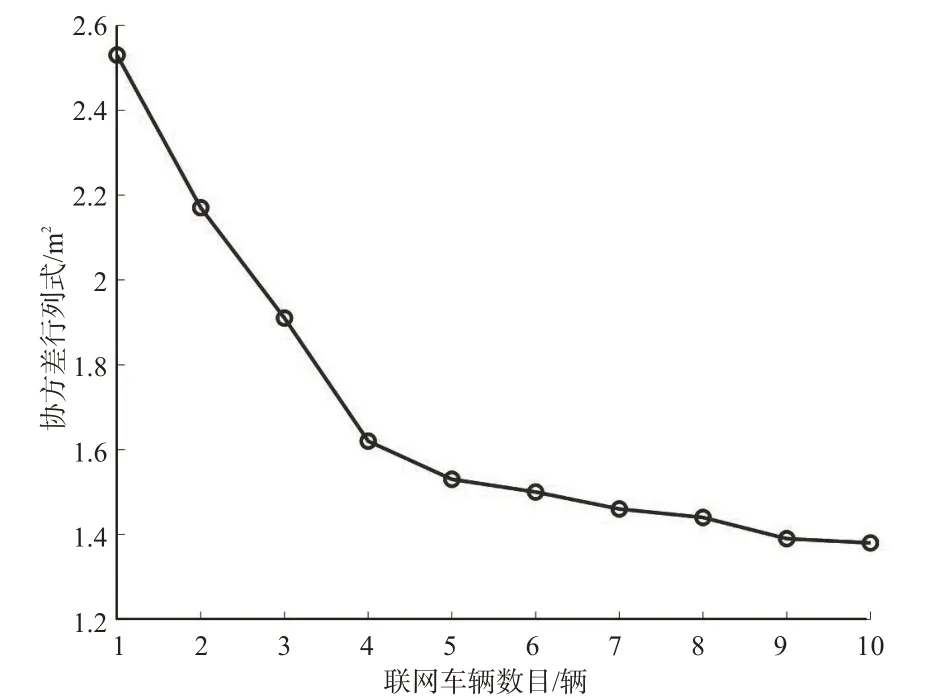
图9 协方差行列式与联网车辆数目之间的关系Fig.9 Relationship between covariance determinant and the number of connected vehicles

3 实测分析

3.1 测试场景描述

目前，测试中用到的智能网联车载终端无法实现实时协同地图匹配，仅能实现基于DSRC通信的定位数据信息同步，所以实际测试采用离线数据处理的方式进行，将GNSS定位数据采集后再利用协同地图匹配算法进行处理。动态测试的真实参考值是1段车辆行驶轨迹，选择使用M600 GImini GNSS接收机的定位结果作为真实参考值。该接收机是由司南导航研发的高精度GNSS定位接收机，支持载波相位差分定位和惯性导航定位，利用千寻位置提供的载波相位差分定位时动态水平定位精度可达10 mm+10-6，高程定位精度达20 mm+10-6[16]。测试所用的智能网联车载终端基于u-blox公司设计生产的VERA-P1型DSRC通信模块设计，定位模块为u-blox M8N，标称水平定位精度2.5 m（CEP）[17]。该终端能够实现对GNSS原始定位数据的采集和共享，包括伪距、卫星编号以及时间戳等，通信范围约为1 km。测试过程中使用4台测试车辆，测试设备连接示意图见图10，图10中所示天线置于车顶且增益均为50 dB。对于M600 GImini接收差分信息所需的4G天线经测试置于车内信号良好，故将其置于车内。实际测试过程中为更加贴近真实情况，4台测试车辆以10～30 km/h的时变速度在DSRC通信范围内跟随行驶[18]。此外，为了更加清晰地分析算法在实际应用场景中的定位效果，采用蒙特卡洛方式进行10次独立重复实验，测试环境和参数设置参见表4。

表4 测试环境和参数设置Tab.4 Test environment and values of parameters

图10 实车测试场景及设备连接示意图Fig.10 Test scenario and equipment connection

数据测试完成后根据智能网联车载终端原始GNSS定位数据得到接收机位置、时钟偏差和时钟漂移的初始值；由M600 GImini接收机定位结果与实测伪距的差值估计公共偏差的初始值作为算法公共偏差初始值以供协同地图匹配算法使用。

3.2 测试结果分析

数据采集完成后根据GNSS 原始数据的时间戳选择一组同步数据代替仿真数据，通过Matlab实验平台进行算法验证。为了保证算法的实时性，处理过程使用50个粒子进行滤波估计，统计时间为500 s，其他参数设置参见表1。实验结果见图11～14，其中图11为实际测试过程中水平方向的定位误差及协方差行列式。

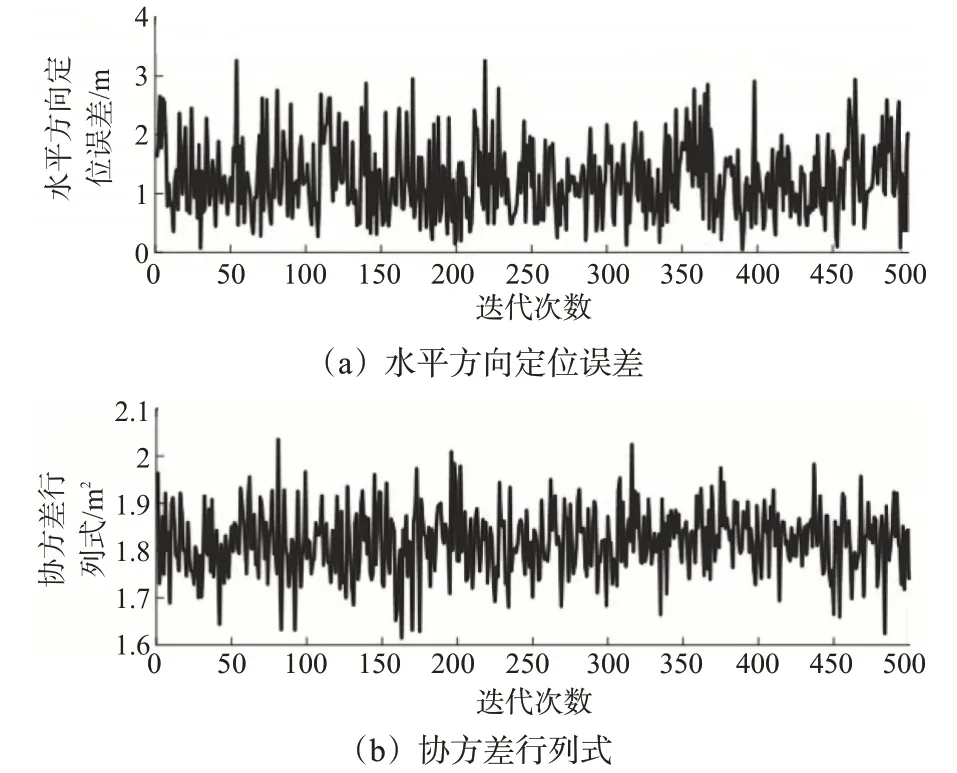
图11 水平方向定位误差和协方差行列式Fig.11 Horizontal positioning error and covariance determinant

图12为测试过程中，协同地图匹配算法对公共偏差的估计误差。公共偏差的真实值以M600 GImini GNSS接收机定位结果与实测伪距的差值计算得到。

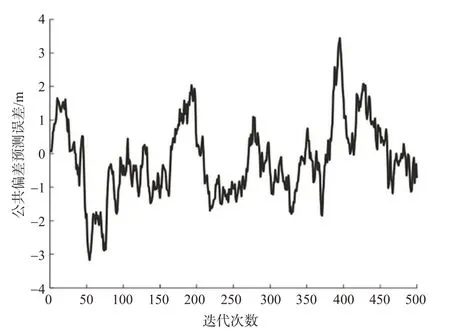
图12 公共偏差估计误差Fig.12 Error estimate of common deviations

图13为目标车辆在协同地图匹配情况下对应的水平定位误差分布，图14为实际测试结果中GNSS原始定位、单车地图匹配以及协同地图匹配3种方式对应的水平方向定位误差累积分布曲线。

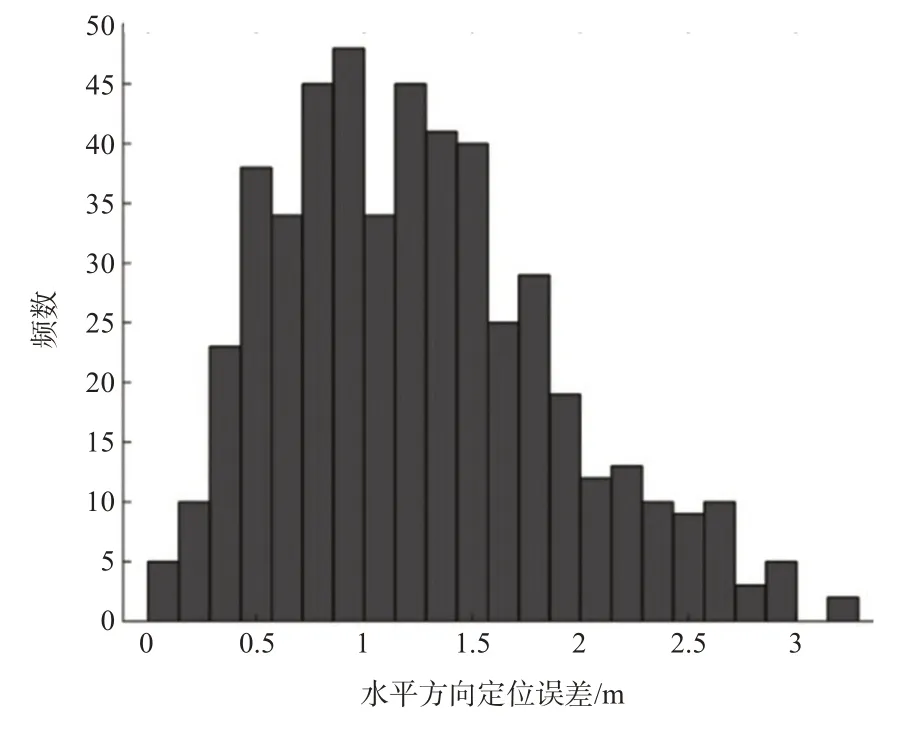
图13 水平方向定位误差分布Fig.13 Distribution of horizontal positioning errors

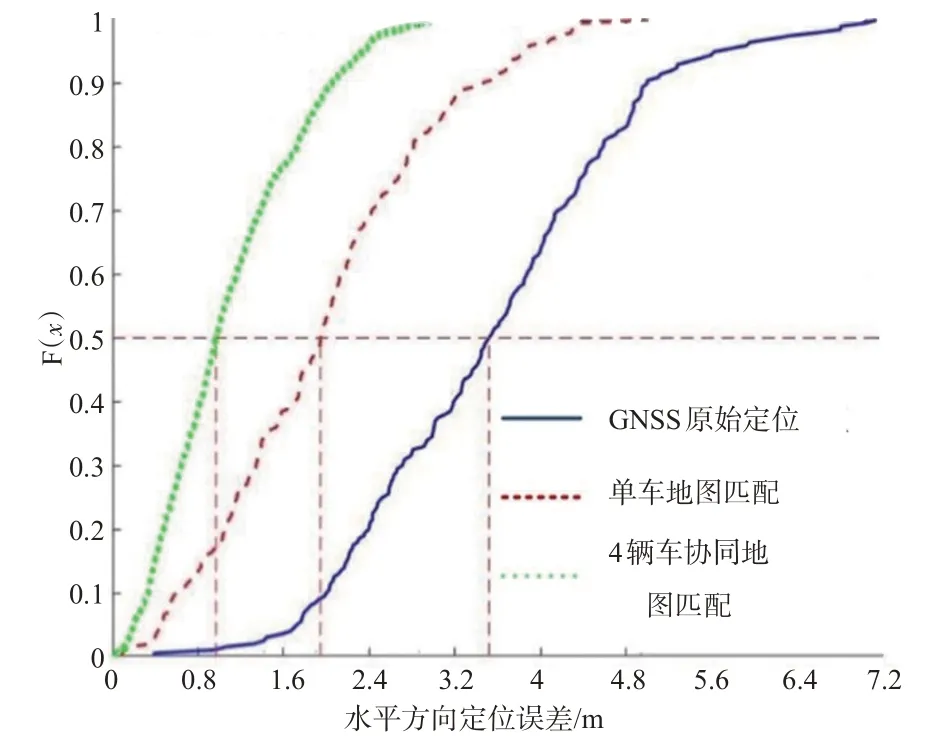
图14 水平方向定位误差累积分布曲线Fig.14 Cumulative distribution curves of horizontal positioning errors

通常情况下用圆概率误差（circular error probable，CEP）来描述GNSS接收机的定位精度。以5 m CEP为例，它表示以定位真实值为圆心，5 m为半径画圆，有50%的定位结果会落在圆内，即该GNSS接收机定位误差在5 m范围内的概率为50%，其定义见式（6）～（7）[19]。

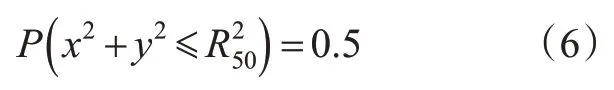
式中：x和y分别为定位结果的北向和东向误差。

为了更加清晰地对比实验结果，这里将10次蒙特卡洛独立重复实验的均值以及GNSS接收机和单车地图匹配定位结果统计见表5。

表5 GNSS，单车地图匹配以及协同地图匹配测试结果Tab.5 Experimental results of GNSS,single map matching,and cooperative map matching

根据实际测试结果与仿真实验结果对比可知，将实际定位数据应用到协同地图匹配算法中，算法的定位精度比仿真数据有一定程度的降低。在实际应用中，GNSS定位结果受到信号遮挡、传输延迟、多径效应等多种因素的影响，与仿真过程存在一定的差异，这些因素造成的定位偏差也很难完全消除。但是，将该定位结果与原始GNSS接收机以及单车地图匹配定位结果进行对比发现，该算法的水平定位误差范围分别降低至原始GNSS接收机的41.03%和单车地图匹配的56.80%。同时，利用协同地图匹配算法，车辆的统计定位精度由原来的3.58 m提高到1.06 m。这表明该算法在实际应用中也具有较好的定位效果，能够提高传统GNSS接收机的定位精度。

4 结束语

本文对智能网联环境下的低成本、高精度定位进行研究，利用联网车辆的位置信息和道路约束条件消除公共偏差，提高定位精度，并针对协同地图匹配算法中容易出现的“粒子耗尽”问题，建立了基于自适应遗传Rao-Blackwellized粒子滤波的协同地图匹配算法模型。仿真实验结果表明：该算法与协同地图匹配应用的传统粒子滤波和卡尔曼平滑粒子滤波相比，具有更高的定位精度和估计准确性。其定位精度受粒子数目影响较小，但是实时性受粒子数目影响较大，因此实际应用中应合理选择粒子数目。算法定位精度受联网车辆数目影响，且随着联网车辆数目的增加，车辆定位精度会有一定程度的提高，但由于随着道路约束条件的增加，车辆定位的误差范围逐渐减小，出现在道路外侧的粒子数目也会变少，此时约束条件对粒子无法起到约束作用，因此二者之间并非线性关系，随着联网车辆数目的增加，精度的提升效果也会逐渐减弱。实际测试结果表明：在单车地图匹配可以有效提高车辆定位精度的情况下，使用协同地图匹配算法能够进一步提高车辆定位精度。该算法定位的水平定位误差分别是原始GNSS接收机的41.03%和单车地图匹配的56.80%。此外，协同地图匹配算法将原始GNSS接收机的定位精度由3.58 m提高至1.06 m，能够得到较好的定位效果。在未来的研究中，还可以在当前仿真和离线数据处理的基础上，利用智能网联车载终端实现算法移植和实时协同地图匹配的测试。