时变阻尼系数的等温可压缩欧拉方程组光滑解的爆破研究
于慧敏 隋 莹
( 山东师范大学数学与统计学院, 250358, 济南 )
1 引 言
在拉格朗日坐标系下, 本文考虑含时变阻尼系数的一维可压缩Euler方程
(1)
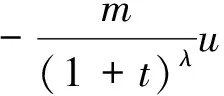
(τ,u)(x,0)=(τ0,u0)(x)
(2)
下古典解的爆破现象.
关于双曲守恒律方程组的奇性形成问题, 已有大量的文章进行了研究. 文献[1]中有关于该问题研究的综述. 总体来说, 在一维空间中, 小初值解(即在常状态附近的解)的爆破结果已经比较完善[2-6].但是, 目前关于大初值问题的研究还远远不够. 对于2×2的一致严格双曲系统, Lax[3]在1964年给出了一个奇性的形成结果, 这种方法可直接应用于γ>3的p-系统的研究中, 但是对于3>γ≥1的情况Lax的方法并不适用, 其主要的原因是原来的p-系统随着t→∞可能失去严格双曲性.
陈庚等人[7]通过研究p-系统在3>γ>1时密度的下界估计, 成功地绕开了Lax[3]文章中所需要的严格双曲条件, 并得到了等熵(γ>1)p-系统“大”初值解爆破的充要条件.众所周知,阻尼效应从能量估计的角度来看不能提高解的正则性. 一个自然的问题为:若在p-系统中考虑(与时间相关的)阻尼效应的影响, 光滑解的爆破会如何变化呢?
另外, 一般来讲系统(1)光滑解的爆破有三种重要的形式:
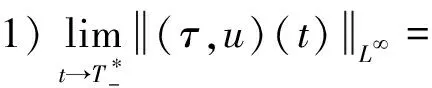

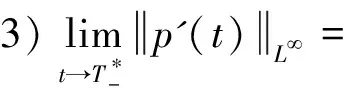
若方程组(1)、(2)的古典解爆破, 那么它们是以1)-3)中的哪种形式产生的奇性呢?是否形成了“激波”(即未知函数自身有界但导数爆破)?这些都是值得研究的问题.
2020年,陈庚等人[8]研究了含时变阻尼可压缩Euler方程的Cauchy问题光滑解的整体存在性与有限时间爆破的问题. 作者指出阻尼系数中的参数λ和m会影响方程光滑解的全局性. 然而, 文献[8]中有个重要的假设:即初始的两个Riemann空间变量必须是单调的. 在本文中,研究带有时间依赖阻尼系数的等温Euler方程光滑解的激波形成问题, 值得指出的是本文并不需要初始Riemann不变量的单调性假设, 并且本文所采用的方法可应用到γ>1的情况.
受文献[3]与文献[7]的启发, 本文定义了与Riemann不变量空间导数相关的两个变量, 并证明了这两个变量沿着相应的方向导数满足Riccati方程, 利用Riccati方程解的形式得到了带有时变阻尼系数的等温Euler方程组Riemann不变量导数爆破的充分条件. 特别地, 当λ=0时, 系统(1)转化为具有常系数阻尼的等温可压缩Euler方程, 当m=0时, 系统(1)对应于著名的等温Euler方程. 在这两种情况下,可以得到光滑解存在的充要条件. 另外, 作为主要结论的副产品,本文给出了初值问题(1)、(2)任意光滑解密度的下界估计, 这对进一步研究该方程组整体解的其他性态, 诸如大BV解的整体存在性、长时间行为等提供了基础.
2 预备知识和Riccati型方程
对于齐次可压缩的等温Euler方程
(3)
用c表示非线性拉格朗日声速, 则
(4)
通过计算, 可以得到方程(3)的两个特征值为
λ1=-λ2=c.
(5)
两个Riemann不变量是
(6)
利用Riemann不变量z和w将方程(1)对角化为
(7)
(8)
其中
(9)
设α=wx,β=zx, 现定义两个新变量
(10)
(11)
下证y和q满足以下引理1:
引理1设τ(x,t)和u(x,t)为方程(1)、(2)的古典解,y和q如(10)式与(11)式所定义, 则y和q满足如下方程
y'=-a2y2-a0,
(12)
q、=-a2q2-a0,
(13)
其中
(14)
(15)
证由(7)式可得

则
(16)
又由(4)式和(6)式得
因此(16)式变成
(17)
同理可得
(18)
以上两个方程(17)和(18)是关于α和β沿两个不同特征方向的方程.
下面将Riemann不变量关于空间变量的导数(α或β)转化成比容沿特征线的导数, 从而实现方程(17)和方程(18)的解耦. 由(1)式和(9)式得
(19)
因此
再由(17)式得
(20)
(21)
即
(22)
现定义一个新的变量
(23)
则
从而(21)式可以变为
(24)
这里
(25)
令
(26)
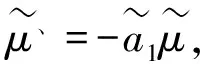

(27)
则(24)式变成
y、=-a2y2-a0,
其中
(28)
(29)
同理, 由(1)式和(9)式可得
故
并由(18)式得
因此
(30)
类似(23)式,定义一个新的变量
(31)
因此
故(30)式可以写成
(32)
q'=-a2q2-a0,
(33)

3 密度的下界估计
引理2由问题(1)与(2)的古典解τ(x,t)和u(x,t)出发所定义的变量y和q,可得下面的估计:
y(x,t)≤max {1,sup(y(x,0))}∶=Y,
(34)
q(x,t)≤max {1,sup(q(x,0))}∶=Q.
(35)
证当λ>0时,a0,a2都是非负的, 很容易由引理1证得引理2成立.
下面给出任意经典解的密度随时间变化的下界估计, 这一点在本文主要结论的证明中起着非常重要的作用.
引理3对于方程组(1)与(2)的古典解τ(x,t)和u(x,t), 下述结论成立:
(36)
其中Y和Q如(34)式和(35)式中所定义.
证当λ≠1时, 由引理2和(7)式、(10)式可得
(37)
类似地, 由引理2和(8)式、(11)式可得
因此
对上式两边关于t积分可得
(38)
于是有
τ-1(x,t)=ρ(x,t)


(39)
当λ=1时, 与上面的证明类似可得
(40)
从而可以得到
证明完毕.
4 主要结果
定理1假设初值(τ,u)(x,0)∈C1(R)满足下述条件:
1)τ(x,t),|u(x,t)|,|τx(x,t)|,|ux(x,t)|一致有上界, 即存在某一常数M0>0, 使得
τ(x,t)+|u(x,t)|+|τx(x,t)|+|ux(x,t)| 2)τ(x,0)一致远离零, 即存在δ0>0使得τ(x,0)>δ0; 3) 如果存在某一点x0∈R满足 (41) 或者 (42) 则ux或者τx一定在有限时间内爆破, 即存在t*>0,使得 (43) 证由(12)可得 y'=-a2y2-a0<-a2y2<0, 将上述不等式的两边关于t沿特征积分得 (44) 则 (45) 因此 (46) 由不等式(46)可知:若存在x0∈R使得y(x0,0)<0, 并且 则一定存在有限时间t*使得y(x(t),t)在t*之前爆破. (47) 由(14)式可得 (48) 类似,当λ=1时, 由(40)式可知, 存在一个T>0,当t>T时有 又由(14)式可得 (49) 1) 由Riemann不变区域理论容易知道问题(1)与(2)的古典解τ(x,t)和u(x,t)都是关于时间一致有界的, 即存在M(仅与初值有关)使得0≤τ-1(x,t)≤M, |u(x,t)|≤M, 从而定理1说明形成奇性是由激波引起的. 2) 当m=0或λ=0时, 引理1中的a0=0, 此时, 利用关于标准的Riccati方程的讨论, 可得如下经典解爆破的充要条件的定理2. 定理2假设初值(τ,u)(x,0)∈C1(R),满足: 1)τ(x,t),|u(x,t)|,|τx(x,t)|,|ux(x,t)|一致有上界, 即存在某一常数M0>0, 使得 τ(x,t)+|u(x,t)|+|τx(x,t)|+|ux(x,t)| 2)τ(x,0)一致远离零, 即存在δ0>0使得τ(x,0)>δ0, 则问题(1)与(2)存在整体古典解的充要条件为:对任意x∈R都有 和 即初始Riemann不变量处处不压缩(wx(x,0)≥0,zx(x,0)≥0,∀x∈R),原方程存在整体古典解;只要w或z存在一点压缩, 原方程的解就会爆破. 3) 由定理2可知, 相比于p-系统, 对于带有阻尼的p-系统需要初始Riemann不变量“更大”的压缩性(即(41)式和(42)式)才能保证古典解的爆破. 这说明从能量估计的角度来看阻尼效应虽不能得到系统解更高的正则性, 但还是能在一定程度上阻碍系统古典解的爆破.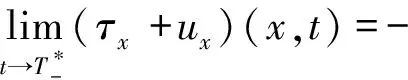




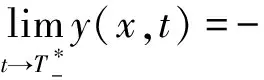
5 评论和展望

