三相异步电机矢量控制系统

陈蕾蕾，程林琳，熊兴中

（四川轻化工大学自动化与信息工程学院，四川 宜宾 644000）

引 言

共振弯曲疲劳试验平台可以用来进行海洋立管、钻柱等大直径旋转结构的疲劳测试试验，而电动机是共振弯曲试验平台加载系统的主要部件，为疲劳试验提供动力。异步电动机具有结构简单、可靠性高、价格低廉、坚固耐用、易于维护等特点［1］，因此可以在共振弯曲疲劳试验中选用三相异步电机作为加载系统部件。

早期的电压恒定控制和频率控制等理论研究异步电机的控制原理和特性都是建立在异步电机处于稳态时的数学方程理论基础上，20世纪的德国学者首次提出了矢量控制的原理，异步电机的矢量控制动态特性的研究也有了很大的提高，异步电机的矢量控制理论已经为交流传动的高性能控制技术奠定了坚实的理论基础［2］。随着电机控制系统技术的进步与发展，电压的空间向量调制理论被引入到逆变器及其控制中，形成了一种称为空间向量脉宽调制的理论［3］（简称SVPWM）。空间向量脉宽调制原理是通过切换逆变器6个功率启动开关的闭环状态，以一个内切多边形逼近椭圆型的方法来逼近发电机空间中气隙的一个理想圆型旋转磁场［4］。该方法可以有效地削弱驱动器和电机的转矩脉动，提高了驱动器在电力系统中运行时的性能。与其他传统的正弦波脉宽调制（以下简称SPWM）方式相比，SVPWM更加易于直接实现完全数字化的控制，能够有效地抑制交流电压和谐波，提高了直流输出电压的利用率［5］。

文献［6］在Simulink中采用转速、磁链双闭环的异步电机矢量控制系统仿真，有效抑制了负载扰动，实现恒流升速。文献［7］在Simulink中验证了改进SVPWM后的异步电机矢量控制系统，可使转速跟踪性增强。文献［8-9］研究的是无速度传感器的异步电机矢量控制系统算法，但考虑实际工程的应用，一般使用由速度传感器的矢量控制算法。文献［10］介绍了PLC技术与变频器组合，使得三相异步电机能够实现调向、调速控制。文献［11］中使用带有ProfiBus总线接口的西门子MM440变频器作为实现PLC与三相异步电机之间的信号转换设备，采用一种改进的积分分离PI控制算法来实现系统控制。文献［12-14］基于DSP建立了异步电动机的矢量控制系统，并在一定程度上提高了电机的控制速度。

本文针对三相异步交流电机的矢量控制系统进行模块化设计。首先在Simulink环境中建立矢量控制系统，其中SVPWM采用带死区的设计方法，观察实验结果分析其性能；其次用硬件描述语言对各部分模块编译设计，SVPWM作为此矢量控制系统的核心部分，在采用硬件描述语言设计时也实现了死区可调；最后使用Modelsim对各部分模块进行波形仿真验证，为提高电机运行、调速性能提供重要依据。

1 矢量控制系统原理

电机对转速的控制，归根结底是通过对其转矩的控制实现的。在从三相静止坐标系变换到两相旋转坐标系后，电机的控制变得简单。矢量控制原理图如图1所示，图中可见矢量控制系统主要由SVPWM模块、PI控制模块、Clark变换、Park变换以及Park反变换模块等组成。

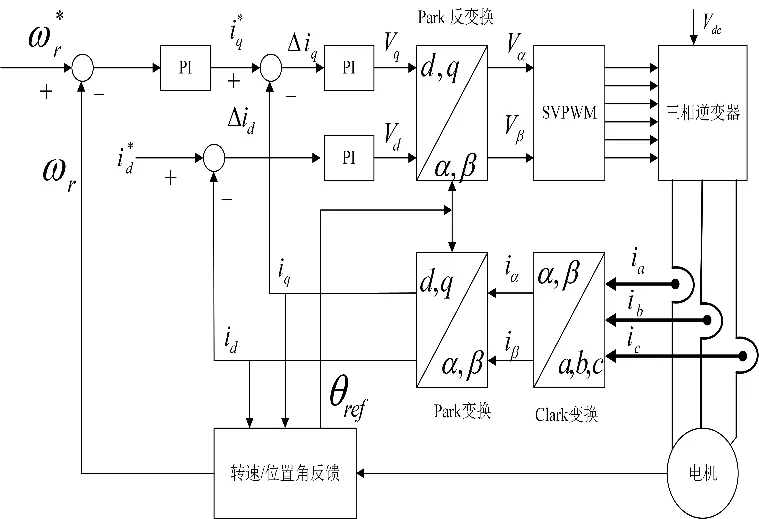
图1 矢量控制系统原理结构图

1.1 SVPWM模块

空间脉宽调制（SVPWM）主要是从三相输出电压的一种整体响应效果入手，使其所产生的磁链运动轨迹呈圆形,从而促进输出的电流和频率接近于理想正弦波。其具体工作原理如下：三相桥6个开关可以构成8个开关状态，包括6个非零矢量U1(001)、U2(010)、U3(011)、U4(100)、U5(101)、U6(110)，以及两个零矢量U0(000)和U7(111)，通过8个状态的不同组合来构成定子电压矢量Vref［15］，满足式（1）:

式中，V k、V k+1为开关状态矢量，T s为PWM周期，T k、T k+1为相应的开关状态矢量的导通时间，T0为初始开关状态矢量的导通时间，由下式计算：

式中，Vdc为三相逆变电压，Vα，Vβ为两相静止坐标系α-β下的定子电压。由式（2）即可生成SVPWM波。

1.2 PI模块

PI控制算法简单、鲁棒性好、技术成熟，被广泛用于过程控制、机器人控制、自动化等领域，尤其适用于可建立精确数学模型的确定性控制系统［16］。文献［17］中对异步电机矢量控制的电流环控制器进行了比较研究，为电机矢量控制中电流控制器提供了参考。本矢量控制系统的电流控制采用PI控制算法调节，由于FPGA的控制实际是一种离散数字控制，为保证离散系统和连续系统具有相同的稳定性，采用双线性变换，得到PI调节器迭代公式为：

其中，P(k)为比例，I(k)、I(k-1)为积分，K P为比例增益，K I为积分增益，e(k)、e(k-1)为误差输入。

1.3 Clark模块

Clark变换指三相定子坐标系a-b-c转换到两相定子静止坐标系α-β。Clark变换有功率不变和幅值不变两种形式，由于幅值不变的Clark变换在硬件实现上占用资源较少，与功率不变的情况相比，差别在于 2 3的系数，因此三相电流的幅值不变的Clark变换公式如下：

式中，i a、i b、i c分别表示三相异步电动机的三相定子电流；iα、iβ表示在静止坐标系α-β下的定子电流。

1.4 Park变换及Park反变换

Park变换即两相静止坐标系α-β变换到两相旋转坐标系d-q的变换，关系如下：

式中，i d，i q为旋转坐标系d-q下的定子电流，θ为旋转角度。

Park反变换即两相旋转坐标系变换到两相静止坐标系的变换，如下式：

式中：Vα，Vβ为静止坐标系下的定子电压；V d，V q为旋转坐标系d-q下的定子电压。

Park变换和反变换涉及的正余弦值的实现方法大体有3种：查表法、泰勒级数展开法和CORDIC（Coordinate Rotation Digital Computer）算法。CORDIC算法具有易于实现、可移植性强、精度可调等特点［18］，使用移位与加/减算术运算可求得所需值，适合数字硬件实现。

CORDIC算法基本原理如图2所示。

图2 CORDIC算法原理图

依据原理图可得下式：

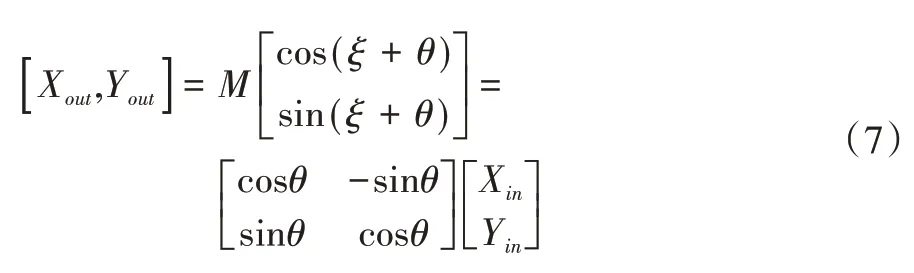
式中：X in，Y i n为输入；X ou t，Y ou t为输出；ξ为初始角度；M为常数；θ为旋转角度。

CORDIC算法使模长产生畸变，需要校正因子补偿。本文中对输入X in、Y i n预先乘以模校正因子K=，其迭代公式如下：

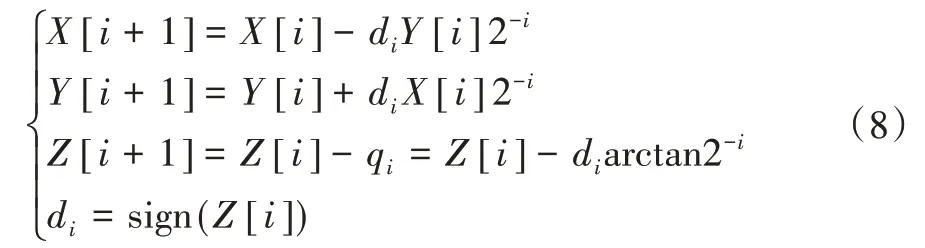
式中，Z[i]为新引入的变量，用来记录每次旋转以后与实际角度之差值。δi为方向信号，定义如下：

2 矢量控制系统Simulink仿真分析

利用Simulink仿真工具，根据图1的原理图搭建了三相异步电机矢量控制模型，得到的电磁转矩、电机转速波形仿真分别如图3、图4所示。

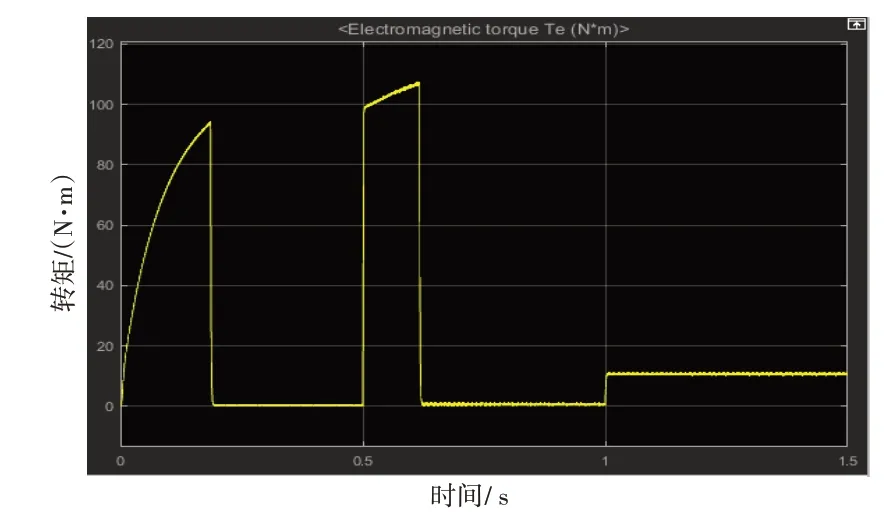
图3 电机转矩变化曲线

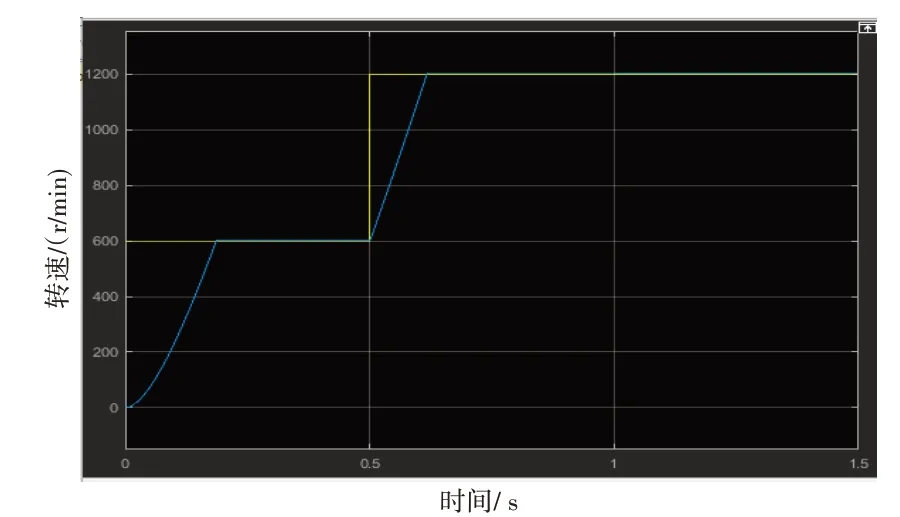
图4 电机转速变化曲线

由仿真波形图4可知，参考转速：在0~0.5 s内为600 r/min，在0.5 s后为1200 r/min。开始时电机转速有一些超调量，但是其动态响应速度较快。当负载在0.5 s变化时，速度转矩和定子电流会发生相应的波动。经过对PI参数的调节后，速度可以快速跟随给定值，但一般在稳定状态下达到给定值可能需要更长的时间。三相电流随正弦波的变化而变化，幅值在负载变化后有明显的幅值跳变，但也能迅速稳定。对于转矩（图3），外部负载扰动有一个动态的向前运动，从0.5 s后参数的转换可以看出电机的各项参数趋于稳定。总之，可以看出，矢量控制系统下的三相异步电机具有很强的稳态性能和抗干扰能力，并且也具有一些动态性能。

3 基于FPGA的矢量控制系统设计验证

3.1 SVPWM模块

SVPWM主要模块首先通过两相电压Vα、Vβ判断空间电压矢量所处扇区位置；然后计算中间变量X、Y、Z；再根据所处扇区计算相邻两个基本电压矢量合成空间电压矢量的时间T1、T2，转化成对应的占空比T cma、T c mb、T cmc，占空比与三角载波比较，输出6路两两互补带死区的PWM，如图5所示。

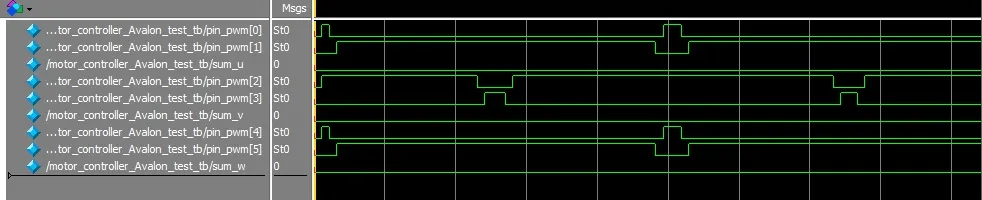
图5 带死区的PWM波

3.2 PI调节器设计

PI模块硬件实现如图6所示。为预防寄存器产生溢出，需要给调节器设置饱和限幅。PI调节器的设计利用积分分离的方式，在积分器输出达到饱和状态时，将积分环节关闭，实现快速去饱和，减小超调的目的。使用场合不同时，调节两个参数K P和K I，以控制角度跟踪系统的带宽，在抑制干扰的同时，保证相位滞后较小，使跟踪系统最优化。在程序内设置限幅u m，当u(k)>u m时，以u m作为输出，假设设定值为1000，当反馈值为1000时，其仿真结果如图7所示。

图6 PI模块硬件实现结构图

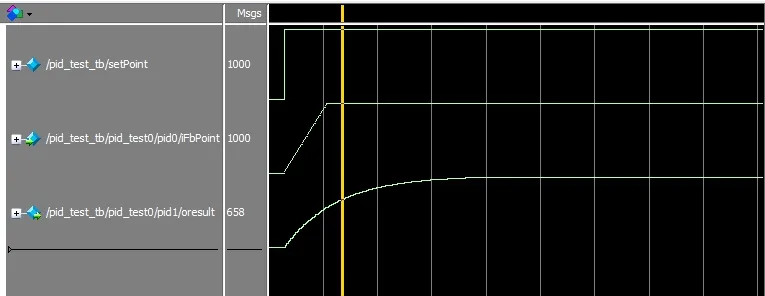
图7 PI模块验证结果

3.3 Clark模块

当输入相位相差120°的三相正弦波电流时，使用Modelsim仿真得到alpha和beta的波形如图8所示，alpha和beta为相差90°的正弦波。

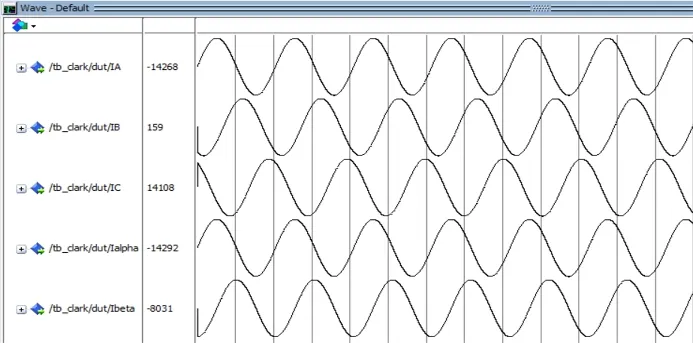
图8 Clark模块验证结果

3.4 Park模块及反变换

由于Park变换和反变换模块的正余弦部分使用CORDIC算法，验证的取值结果如图9所示，图中可见其误差也较小。Park变换验证结果如图10所示，图中可见符合Park变换将两相电流转换成为常数值的基本理论。Park反变换验证结果如图11所示，图中可见符合Park反变换将常数值的电流转换成正弦波的基本理论。

图9 CORDIC算法验证结果

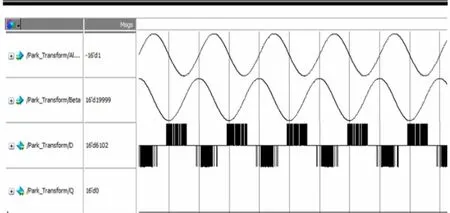
图10 Park变换验证结果

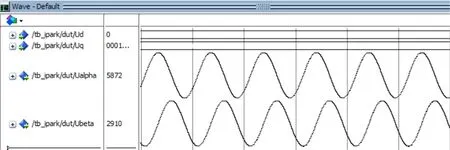
图11 Park反变换验证结果

4 结束语

通过Simulink验证矢量控制系统算法的有效性，再用硬件描述语言描述矢量控制算法的主要分布模块，并用Modelsim仿真验证，为基于FPGA实现的电机矢量控制系统设计提供可行性。因此，在共振弯曲疲劳试验这种实时性要求较高的控制场合，本文方法可以极大地发挥控制系统的性能。