基于参数分层辨识的RMA-UKF算法SOC估计
寇发荣,王甜甜,王思俊,门 浩
(西安科技大学机械工程学院,陕西 西安 710054)
以电池模型为基础的参数辨识是荷电状态(SOC)估计的前提[1]。H.Rahimi-Eichi等[2]提出一种可变窗口的最小二乘法,利用可变窗口特点截取工况信息,以实现参数辨识和SOC估计;朱瑞等[3]提出分布式最小二乘法的锂离子电池建模及参数辨识。这些方法虽然能实现电池参数的在线辨识,但未考虑模型参数之间存在相互干扰的问题,使辨识的模型参数鲁棒性欠佳。针对噪声干扰下SOC估计精度不足的问题,F.F.Yang等[4]用长短时记忆神经网络和无迹卡尔曼滤波(UKF)联合进行SOC估计;M.M.Zeng等[5]使用模糊控制与UKF联合进行SOC和健康状态(SOH)估计;丁洁等[6]提出加权多新息无穷滤波算法进行锂离子电池SOC估计。以上估计均使用σ点集来逼近具有附加高斯噪声的非线性系统,当观测噪声中有污染时,性能将严重退化,使估计结果失真。
本文作者从提高模型参数辨识精度和噪声干扰下SOC估计精度两方面进行分析,提出参数分层辨识架构和鲁棒似然估计的自适应无迹卡尔曼滤波(RMA-UKF)算法,联合进行SOC估计,并使用半实物仿真系统,对噪声干扰下的锂离子电池模型SOC估计算法进行准确性验证。
1 模型建立及参数辨识
1.1 二阶RC模型
等效电路模型的准确建立是SOC估计的第一步。二阶RC等效模型是较好的电池估算模型,同时考虑了电池的瞬态和稳态特性,如图1所示。
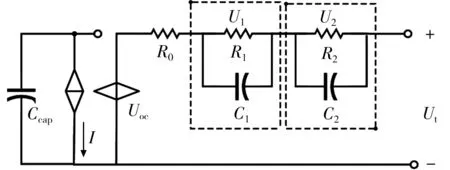
图1 二阶RC模型Fig.1 Second-order RCmodel
图1中:R0为欧姆内阻;R1、R2分别为电化学和浓差极化电阻;C1、C2分别为电化学和浓差极化电容;U1、U2分别为电化学和浓差极化电压;Ut为端电压;Ccap为电池容量;Uoc为开路电压(OCV);I为电流。该等效电路模型的方程为:
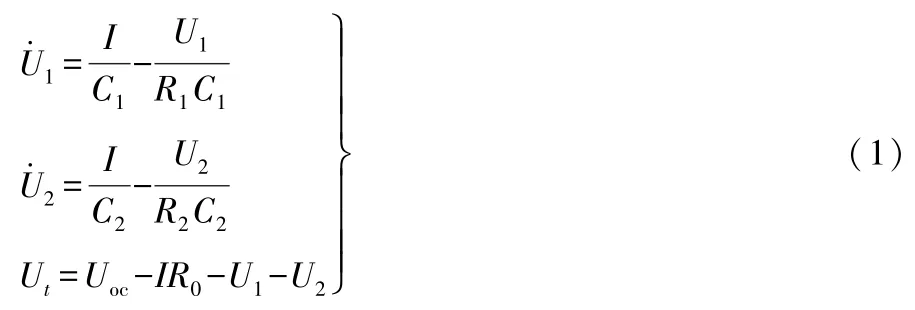
式(1)中:1和2为RC并联环节的电压降。
1.2 开路电压辨识
采用ITS5300型动力电池测试系统(南京产)进行实验。实验对象为18650型锂离子电池(松下公司),正极活性材料为钴酸锂,标称容量为32 Ah,工作电压为2.7~4.2V。
电池在开路状态下的端电压为OCV,选用静置法离线测得。受RC惯性环节的影响,在线辨识测得的是端电压。
OCV-SOC的标定:以1/3C恒流放电,每次放出5%的最大可用容量,静置1 h,可得到OCV,不断循环,直到电压降至2.7V。使用Lsqcurvefit函数拟合OCV与SOC的关系,得到:
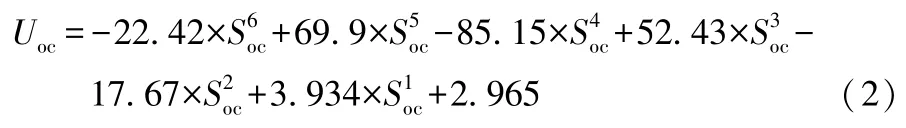
式(2)中:Soc为电池的SOC。
1.3 阻容参数分层辨识
传统参数辨识采用单一的离线辨识方法,在辨识过程中,因极化参数变化较大,导致辨识准确性较低。为了提高参数辨识精度,实验提出阻容参数分层辨识框架,将R0和极化参数分开辨识,不仅可提高辨识精度,还能降低矩阵计算维度。由于R0与电池自身特性有关,采用混合功率脉冲特性(HPPC)实验对参数R0进行辨识,并通过多项式拟合;极化阻抗是由于电池的电化学反应引起内阻值的变化,具有时变特性,采用带遗忘因子的偏差补偿递推最小二乘法(FFBCRLS)实现极化参数的辨识。
1.3.1 欧姆内阻特性辨识
由HPPC特性实验对R0进行离线辨识,一般用两段的平均值来表示欧姆值。R0为突变的压降除以放电电流,即:

式(3)中:Ua、Ub、Uc和Ud分别为HPPC实验前静置平衡点处的电压、放电瞬间下跌电压、放电10 s后电压及放电结束后的回弹电压。
通过MATLAB中的cftool工具箱对R0拟合,得到:
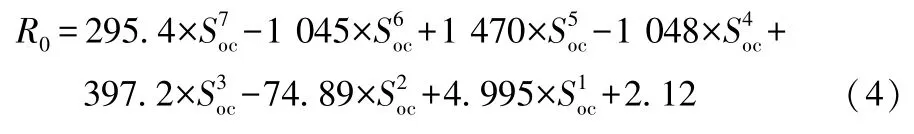
1.3.2 极化参数在线辨识
考虑到极化参数的时变性,采用FF-BCRLS对极化参数进行辨识。电池系统简化成I为输入、Ut为输出的单输入输出系统。分析电池模型,建立并求解系统的状态方程,进而推导出等效电路模型的R1、R2和C1、C2等参数。
将式(1)所示的离散状态空间方程化为差分方程形式:
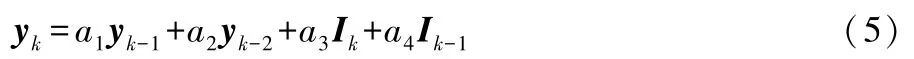
式(5)中:下标k表示当前时刻,下标k-1表示前一时刻,下标k-2表示前两时刻;a i(i=1、2、3、4)为常系数;I和y分别为系统的输入和输出矩阵。

式(6)中:h和θ分别为系统的数据矩阵和参数矩阵。
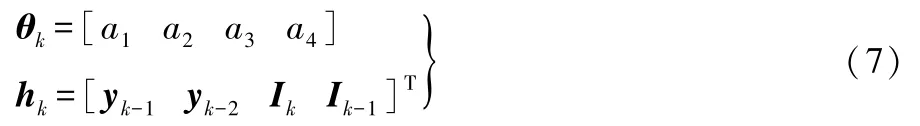
式(7)中的待定系数a1、a2、a3和a4为:
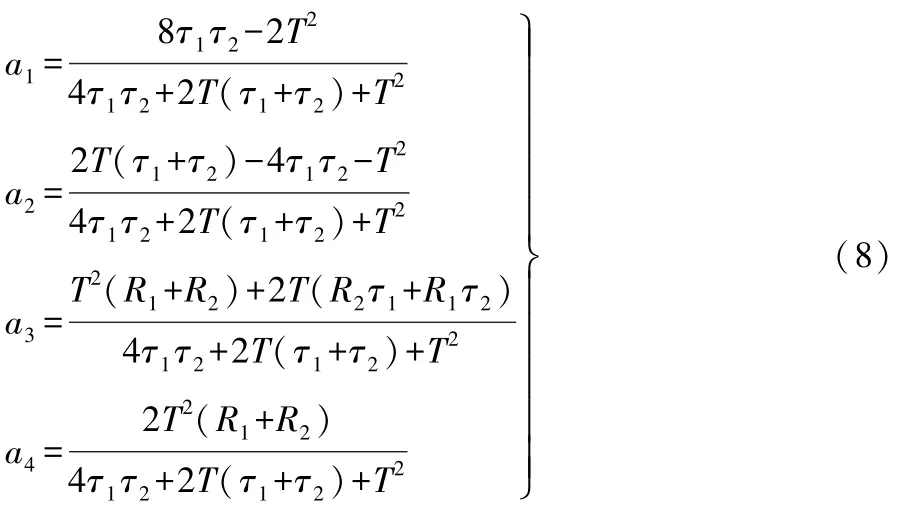
式(8)中:τ1和τ2分别电化学和浓差极化的时间常数;T为采样时间间隔。
FF-BCRLS具体递推过程如下:
①计算系统输出y k和估计误差e k

②计算增益矩阵K k

式(10)中:λ为遗忘因子;P为协方差矩阵。
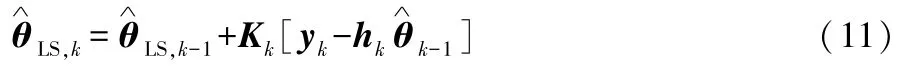
④误差函数J k计算

⑥更新协方差矩阵P和偏差补偿估计值
最后,进行参数计算:
2 基于RMA-UKF算法的SOC估计
RMA-UKF算法在传统UKF的基础上,通过损失函数最小化来解决问题,得到修正因子来修正噪声协方差矩阵,并利用量测数据过滤系统随机噪声,解决噪声干扰问题,提高SOC估计精度。假定k时刻系统状态量为x k,系统输入为u k,系统观测量为z k,以f(x k,z k)为系统状态方程,h(x k,u k)为量测方程,得到系统空间方程:

式(18)-(19)中:A为状态转移矩阵,用来联系前后两个时刻的系统状态;B为输入控制增益矩阵;C为量测矩阵;D为前馈矩阵;ηT为温度修正系数,取值1;ηc为放电倍率的修正系数,实验设定为0.97;Cmax为电池最大可用容量,取值为32 Ah;ω和υ分别为相互独立的量测高斯白噪声。
RMA-UKF通过修正因子修正噪声协方差矩阵来实现系统的自适应性和容错性。UKF算法可参考文献[7];修正因子的推导如下。
由式(18)构建非线性回归模型:

式(21)中:R k为UKF算法的观测噪声协方差矩阵。

定义损失函数J(x k):

函数ϑ(ζ k)的表达式为:
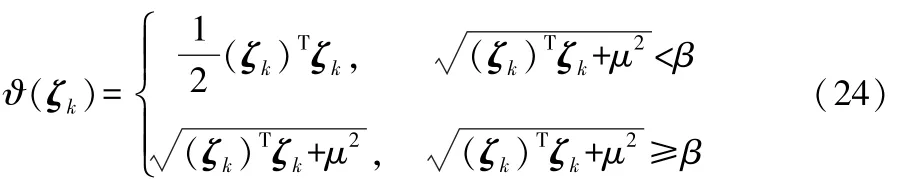
式(24)中:β为回归损失函数参数值,为了达到所需的估计精度,需要合理选择,文献[8]建议β取1.345。



由式(22)可得到环境ζ k,再对φ k作进一步展开:
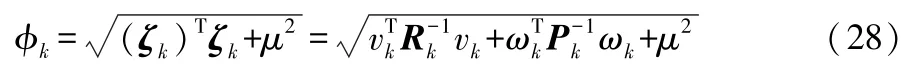
实际上,真实状态值不可知,代入的是外推估计值,从而ω k=0,因此有e k为υ k,定义
构造修正因子Ω:

通过修正因子对观测噪声协方差进行重构,得到修正后的协方差矩阵为:

由式(28)和(29)可知,修正因子Ω和φ k都是对观测噪声协方差矩阵进行修正,由式(30)可得:

式(31)中:λ k=1/γ k。
时间更新阶段、量测更新阶段,观测预测值的计算与UKF算法相同,互协方差P zz,k/k-1以及滤波更新的公式为:
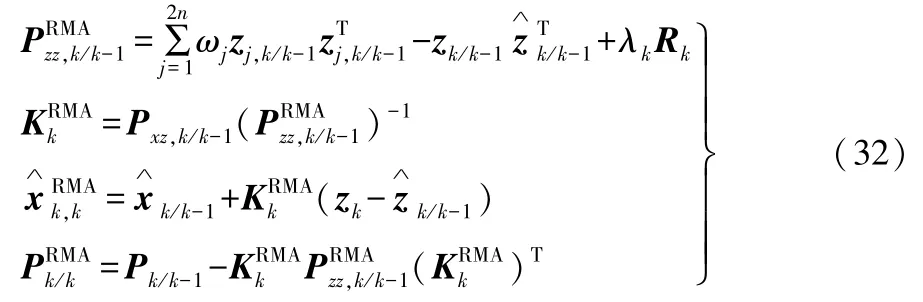
式(32)中:k/k-1代表k-1时刻到k时刻的值;j为状态估计结果中第j个σ点。
3 实验设计与结果分析
3.1 快速控制原型实验设计
采用MicroAuto Box硬件(德国产)进行算法模型的快速控制原型(RCP)验证,通过搭建半实物仿真实验平台,将PC端MATLAB/Simulink中搭建的控制算法模型、MicroAuto Box硬件和动力电池测试系统结合起来,完成算法的在线验证。
3.2 模型参数分层辨识精度验证
为验证提出的参数辨识方法的精确性,以美国城市道路循环工况(UDDS)作为参数辨识的验证工况。将传统参数辨识法[9]、分层参数辨识法计算得到的端电压分别与实测端电压数据进行对比,结果如图2所示。
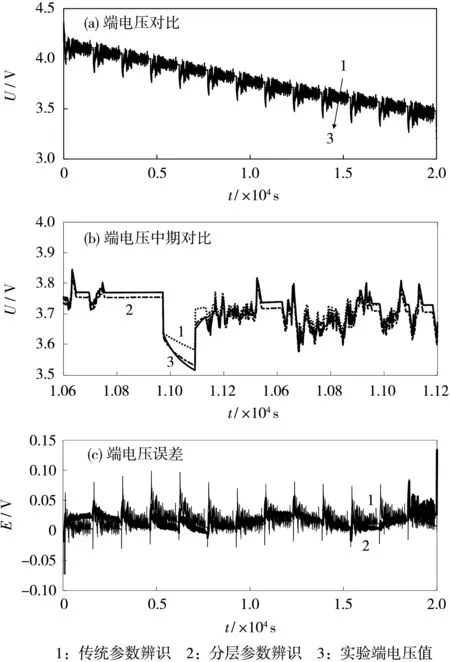
图2 端电压以及误差对比Fig.2 Comparison of terminal voltage and error
从图2(a)可知,在放电初期,传统参数辨识法因参数初始化收敛速度缓慢,存在较大偏差;而分层参数辨识法收敛速度较快,误差较小。放电后期电池SOC过低时,电池内部化学反应不稳定,导致辨识参数剧烈变化,分层参数辨识法的误差略低于传统参数辨识法。从图2(b)可知,因分层架构具有较好的时变性和参数抗干扰性,可在线自适应地调节参数。从图2(c)可知,相比于传统参数辨识方法,分层参数辨识法的效果较好,端电压误差基本维持在合理范围内,波动较平稳,能较好地描述实际输出情况。
3.3 UDDS工况SOC估计精度验证
为进一步验证RMA-UKF算法在有噪声干扰下的精度以及鲁棒性,实验选用UDDS工况进行锂离子电池动态性能测试。验证RMA-UKF算法的鲁棒性时,与传统UKF算法[6]进行对比。无高斯噪声干扰时两种算法的估计结果见图3;有高斯噪声干扰时两种算法估计结果见图4。
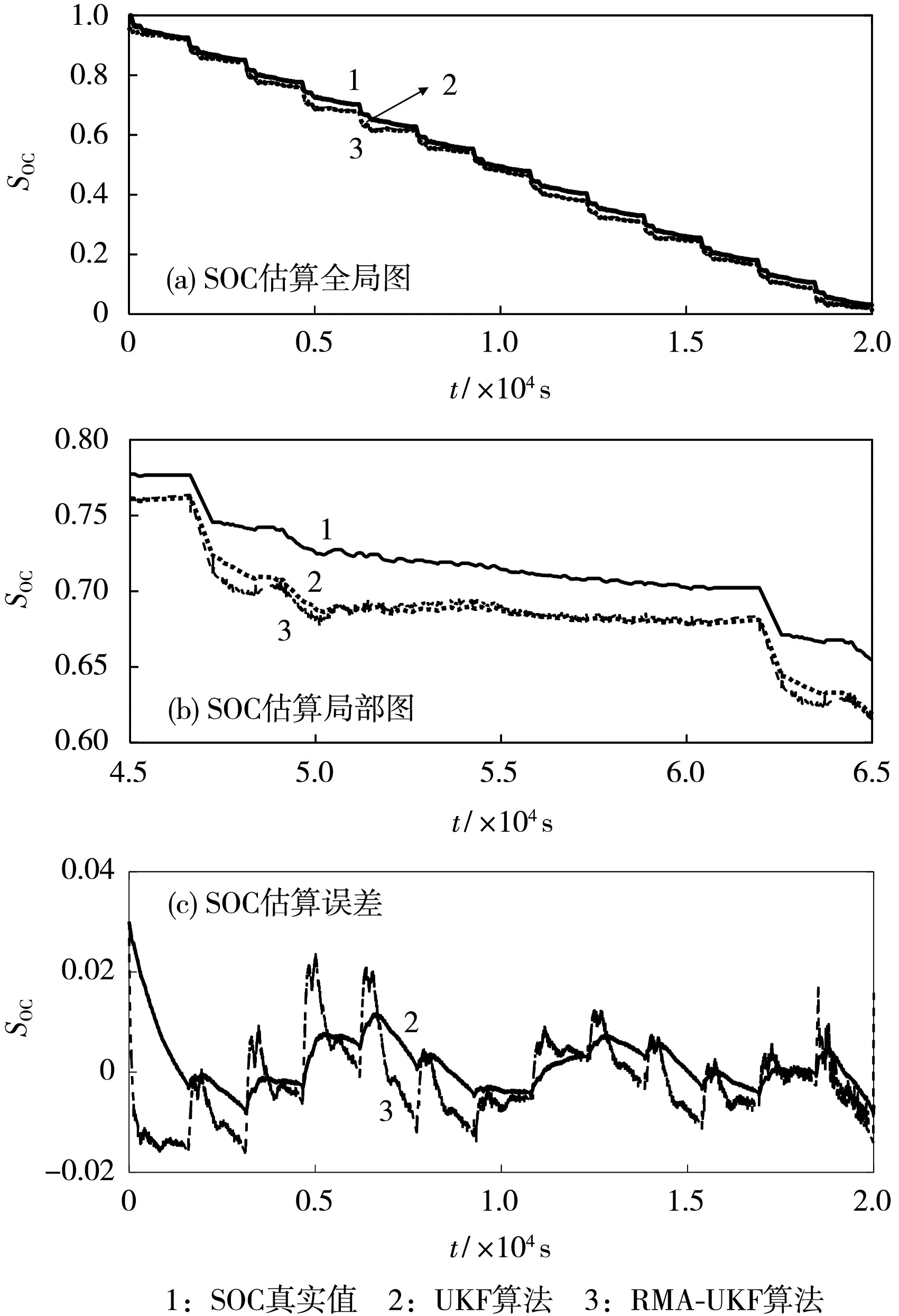
图3 无高斯噪声干扰的SOC估计结果Fig.3 State of charge(SOC)estimation results without Gaussian noise interference
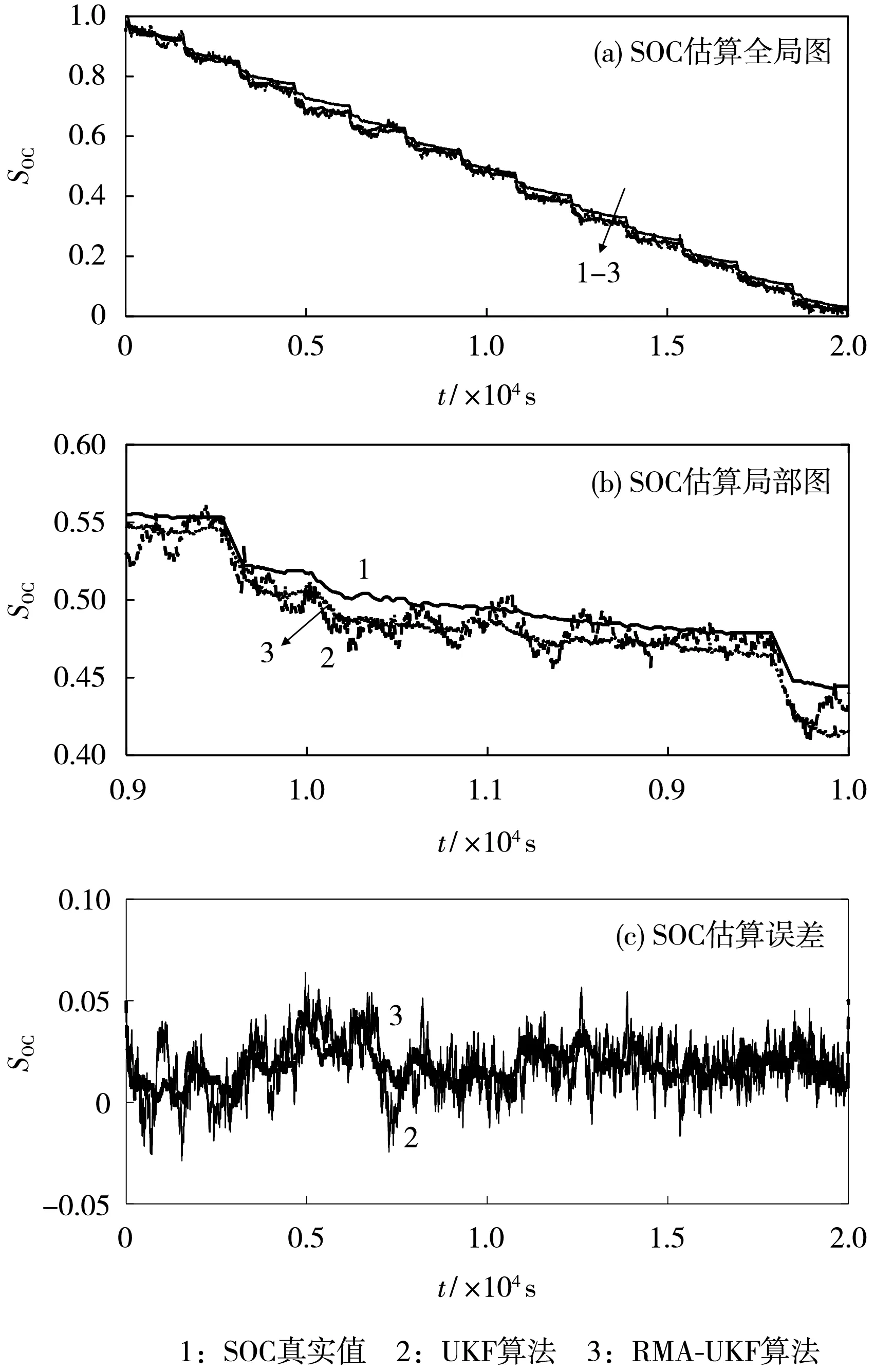
图4 有高斯噪声干扰的SOC估计结果Fig.4 SOC estimation results with Gaussian noise interference
从图3(a)、(c)可知,在无高斯噪声干扰的情况下,放电初期RMA-UKF算法因存在噪声协方差补偿部分,相比于传统UKF算法能更快地收敛到真实SOC值,证明RMA-UKF算法对存在初始误差的系统具有较高的抗干扰性。在放电中期和后期,RMA-UKF算法有较强的跟随能力,从图3(b)可知,RMA-UKF算法优化噪声协方差的精度高于传统UKF算法,整体误差略低。
从图4(a)、(c)可知,当附加高斯噪声干扰时,用UKF算法估计SOC,曲线存在严重的波动,RMA-UKF算法的估计精度优于传统UKF算法。RMA-UKF算法可充分利用每一步测量的数据,根据新测量的信息得到修正因子,并及时修正观测噪声协方差矩阵,增强对噪声滤波的效果,因此,对噪声干扰有较好的抑制作用。特别是从图4(b)可知,相较于UKF算法,RMA-UKF算法的误差整体波动小,说明能够在外界噪声干扰下实现电池SOC的精确估计。
3.4 工况误差分析
为更加准确地分析RMA-UKF算法和传统UKF算法的精度及鲁棒性,实验引入最大误差(MAX)、平均误差(MAE)和均方根误差(RMSE)等3个评价指标,对基于RCP平台的实验结果进行分析。误差统计结果如表1所示。
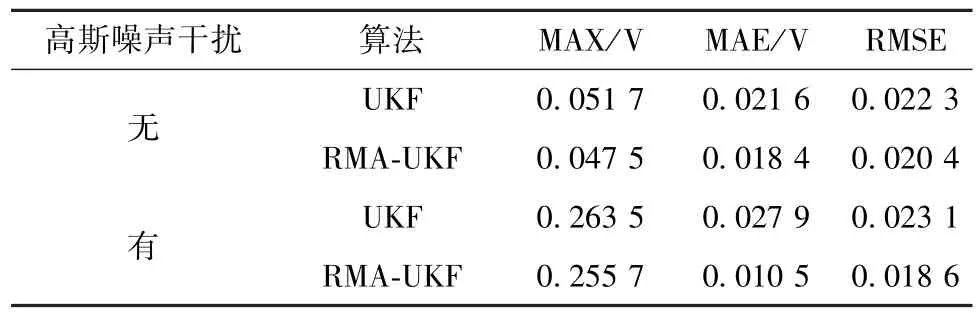
表1 RMA-UKF和UKF算法精度对比分析Table 1 Accuracy comparative analysis of RMA-UKF and UKF algorithm
从表1可知,在无高斯噪声干扰的情况下,整体上RMAUKF算法的误差比传统UKF算法略低,可在各种复杂工况下较好地跟随SOC的剧烈变化。在UDDS工况下,MAX、MAE和RMSE分别降低8.12%、1.48%和8.52%。在有高斯噪声干扰的情况下,RMA-UKF算法的各项误差指标均高于传统UKF算法,能够较好地应对噪声污染,同时保持较高的精度和较快的收敛性。在 UDDS工况下,MAX、MAE和RMSE分别降低2.96%、6.24%和1.95%。实验结果表明,RMA-UKF算法的高精度、高鲁棒性能够满足各种复杂工况下的工程要求。
4 结论
为解决传统电池模型参数极化抗干扰性差的问题,提出双层阻容参数辨识的架构。参数精度验证结果说明:相比于传统参数辨识法,分层辨识法平均误差降低6.7%,能较好反映参数的实时性和无偏性。
针对噪声干扰下全生命周期SOC估计算法适应能力差的问题,提出RMA-UKF算法。该算法通过损失函数最小化得到修正因子,修正观测噪声协方差矩阵,过滤掉噪声污染中的观测野值,能较好地反映SOC估计算法的适应性和鲁棒性。实验结果表明,在无高斯噪声干扰的情况下,RMA-UKF算法平均误差为1.84%,相较于传统UKF算法降低1.48%;在有高斯噪声干扰情况下,RMA-UKF算法平均误差为1.05%,相较于传统UKF算法降低6.24%。

