基于多测点云相似的混凝土坝变形性态关联分析
李子阳,李涵曼,2,李政勰,李永江
(1.南京水利科学研究院水文水资源与水利工程科学国家重点实验室,江苏 南京 210029;2.武汉大学水利水电学院,湖北 武汉 430072;3.河南省水利技术中心,河南 郑州 450003;4.河南省河口村水库管理局,河南 济源 454650)
变形监测是馈控混凝土坝变形性态和安全运行的重要手段[1]。对大型混凝土坝工程来说,一般会在坝顶、廊道、坝基的各个坝段设置包括视准线、引张线、垂线等多个种类、数量众多的变形测点,为获取丰富、全面的大坝变形监测信息提供保障,但多测点海量监测数据给资料及时整编分析和大坝安全性态实时评估预警带来困难。目前工程上常用的大坝安全监测资料分析主要还是建立在单测点序列逐个分析的基础上[2-4],不仅工作量大,而且单测点数据可能受观测误差等影响呈现不稳定性和不确定性,难以判断某个或某几个测点的数据异常变化是否反映了大坝的主要性态变化趋势;而现有的证据组合[5]、模糊推理[6]、关联向量机[7]等大坝多测点融合分析方法,多是考虑空间连续性[8]对大坝安全性态的定性评价,并不能很好地解决大坝不同测点表征大坝性态能力的差异性问题,对海量数据的分析处理仍然效率不高。如何建立混凝土坝多测点数据之间、测点与大坝整体性态之间的关联性并定量体现测点表征大坝性态的能力,是当前大坝安全监测海量数据处理面临的主要问题。
云模型是概率论与数理统计和模糊集交叉融合基础上的一种处理不确定信息的手段,在处理模糊性和随机性上具有很好的表现,由于云理论在表征数据关系方面的优势,其逐渐被用到各种监测数据的处理和趋势分析中。在大坝安全监控领域,杨海彦等[9-10]使用云模型理论来分析大坝的运行状态,并在此基础上提出了一种基于云模型的RBF神经网络改进算法对沉降量进行拟合和预测,以此提高预测精度;Qin等[11]将云模型应用于大坝安全监测,通过正向云发生器和逆向云发生器的使用,实现了“定量—定性—定量”的转化,通过转化后的确定度来确定大坝监测数据是否在正常变化范围内;何金平等[12-13]将云模型引入大坝安全评价,并在此基础上,改进了云合并算法来对大坝进行健康诊断;Wang等[14]提出了一种考虑随机性、模糊性和不完全信息的云模糊模型对堆石坝的堆石压实质量进行评价;朱文锋等[15]建立基于AHP-DEMATEL及云模型的重力坝安全综合评价模型,充分考虑评价指标和评价集之间的不确定性映射,使用云模型来确定其隶属度使得模型评价结果更为可靠;刘可心等[16]利用正态云模型期望曲线和内外轮廓线对混凝土坝的变形进行安全评价,并用实例证明了方法的适用性;Li等[17]利用云参数过程线发现测点的异常值,并提出了使用测点间的相似度实现测点分级的设想。
可以看出,云模型在大坝整体运行性态分析评估方面具有优势。本文进一步使用云模型理论对大坝多测点的安全监测数据进行分析,基于云参数计算表征不同测点反映大坝变形状态的差异,基于云相似系数计算建立大坝各测点之间以及与大坝整体变形性态之间的相关性,并用聚类分析实现大坝测点的差异分组管理及大坝变形性态关联性的高效分析。
1 云模型
1.1 云的概念
云模型是由李德毅院士在概率论和模糊数学的基础上提出的一个定性概念和定量数据相互转化的模型,主要用来描述事物的不确定性。云模型由大量云滴组成,可由云滴群得到云的数字特征[18]。
定义:设x是定量数值表示的集合,U是一个用数值表示的定量论域,C是U上的定性概念,若定量数值x∈U是定性概念C的一次随机实现,x对C的确定度μ(x)∈[0,1]是具有稳定倾向的随机数,即
μ∶U→[0,1],∀x∈U,x→μ(x)
(1)
则x在论域m上的分布称为云,每一个x称为一个云滴。
1.2 云参数计算
云模型使用3个云参数:期望E、熵En和超熵He来表征一个整体概念,是定性概念的定量表示,具有能同时表达概念的随机性和模糊性,并实现不确定性的定性与定量转换的优势[19-20]。期望即数据的平均值,反映云滴在论域C(E,En,He)内分布的期望,是云滴在论域空间分布的中心值,是最能够代表定性概念的点;熵反映云模型的离散程度(随机性)和亦此亦彼性(模糊性),描述了云滴在论域U内可被接受的范围,熵值越大,可接受的范围越大;超熵反映熵的离散程度,是对熵的不确定性的度量,即熵的熵,表现为云滴的凝聚程度,超熵值越小,被接受的程度越高。
云参数的获得是通过逆向云发生器实现的,本质上是基于统计学的参数估计方法,因为云模型是基于不确定性信息的一种模型,所以逆向云算法可根据数据集是否携带确定度信息分为两种算法模型,由于实际工程样本常常不带确定度信息,所以此处采用无须确定度的逆向云算法。输入m个云滴即样本数据xj(j=1,2,…,m),不携带确定度信息的数据集的云参数的计算算法如下。
步骤1设置初始值:
E0=0,En0=0,He0=0
步骤2根据xj分别计算样本期望:
步骤3计算样本方差:
步骤4计算样本熵:
步骤5计算样本超熵:
每增加一个云滴xj,计算一次Ej,Enj,Hej,最后得到m个云参数C(Ej,Enj,Hej),其中j=1,2,…,m。
2 大坝多测点的云计算
云模型是一个定性定量转换的认知模型,从云模型的概念出发,将每个监测数据看作一个云滴,则每个云滴是定性概念在数学模型上的一次反映,且随着云滴的增多,云参数逐渐趋于稳定,这既符合云的特征,也符合常规状态下随着运行时间的增加,坝体整体运行性态趋于稳定的现状。因此在对坝体监测数据分析时引入云模型,通过对云模型参数的分析来对监测数据特征和大坝运行性态特征进行研究,主要思路为:由坝体监测数据建立云模型,根据同一工程监测范围内不同测点的云模型参数相似度计算测点相互之间的相关性,以此进行坝体多测点表征工程变形性态的关联分析。
2.1 云相似度计算
由云模型概念可知,可用3个云参数来表征不同性质的云。当存在多个不同性质的云时,可用相似云考察其相互之间是否具有关联性,以及关联性大小。相似云概念(concept of similar cloud, CS)的提出开始了对云和云之间相似度的研究,不同学者利用云的3个参数E、En、He对云进行度量,描述不同云之间的相似程度,目前几种常用的云相似度计算方法包括SCM云相似度[21]、协同过滤算法LICM[22]以及ECM和MCM云相似性计算[23]。若将混凝土坝监测数据的云模型参数认为是一个向量,由于其测值的云模型参数E反映的是混凝土坝变形的总体性态数据,对于一个正常运行状态的大坝来讲,其监测数据都是在一个正常数值范围内波动,所以E的数值基本不会存在远大于En和He的情况,因此本文采用向量的夹角余弦法来确定大坝多测点表征大坝性态的相似度。
对于n个同一监测类型(水平位移、垂直位移)的混凝土坝变形测点,每个测点以时间顺序的m个测点的监测数据作为待处理数据,表示为如下矩阵形式:
(2)
式中:xij表示第i(i=1,2,…,n)个测点的第j(j=1,2,…,m)个监测数据。
将每个测点看作一个云滴,构建大坝变形监测数据的云模型,云模型参数设置为C(Eij,Enij,Heij)。对于单测点来说,设定每个测点的初试值均为0,随着每个监测数据的加入,通过逆向云算法重新计算测点的最新云模型参数C(Eij,Enij,Heij),第m个测值加入后得到测点的云模型参数C(Eim,Enim,Heim),最后得到n个测点的最终云模型参数,简记为C(Ei,Eni,Hei)。
将混凝土坝各变形测点的云模型参数认为一个向量:
Vi=(Ei,Eni,Hei) (i=1,2,…,n)
(3)
两个向量之间的相似度计算公式为
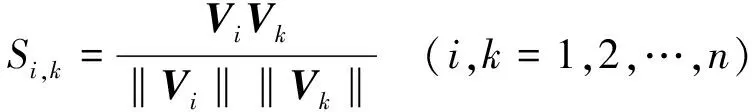
(4)
式中:Si,k表示第i和第k个测点之间的相似度。
为计算测点相互之间的关联性,进一步构建所有测定的云相似度矩阵:
(5)
对于矩阵的每一行,数值相加,最后得到每一个测点相对于其他所有测点的总相似度:
(6)
式中:Si为第i个测点与其他所有测点的相似度。将所有测点组成的云模型集合看作混凝土坝整体变形性态的表征,则Si可认为是第i个测点与大坝整体变形性态的相似度,反映了第i个测点表征大坝总体变形性态的能力。
2.2 云相似系数计算
将测点的总相似度进行归一化处理后得到多测点表征大坝变形的相似系数。假设各测点表征大坝变形性态的重要性相同,根据各个测点的相似度Si,以相似度最大的值Si max作为基准,对各个测点的相似度进行归一化处理,得到各个测点表征大坝总体变形性态的相似系数:
(7)
以相似系数作为测点表征大坝总体变形性态相关性的一个度量因子,根据相似系数的聚类特征对不同测点进行分组划分,从而实现混凝土坝多测点监测数据的差异分组管理及与大坝变形性态关联性的高效分析,能够快速发现异常变形坝段和异常测点。
3 实例分析
某大型水利工程混凝土重力坝长为1 141 m,坝顶高程176.60 m(黄海高程体系),最大坝高117.00 m。大坝共分58个坝段,自右至左分别为右联13~1号坝段、右岸1~7号坝段、泄洪深孔8~13号坝段、溢流表孔14~24号坝段、厂房25~32号坝段、左联33~43号坝段,坝型较为复杂。为监测混凝土坝垂直位移,为右联6~43号坝段每个坝段上下游侧各布置1个精密水准点,共设置100个测点。选取2013年7月至2017年12月各坝段上游共50个测点的监测资料序列进行计算分析。
3.1 全坝段数据分析
采用云模型的方法对大坝垂直位移监测数据进行分析,采用逆向云发生器计算各测点的云参数以及测点之间的云相似度(式(4)~(6));为验证相似系数是否能够准确表示各个测点之间的关联,进一步计算这50个测点的云相似系数(式(7))并按照测点在大坝上的排列顺序绘图,其云参数和相似系数如图 1所示。图中测点编号1~14号为右联6~7号坝段,编号15~20号为泄洪深孔8~13号坝段,编号21~31号为溢流表孔14~24号坝段,编号32~39号为厂房25~32号坝段,编号40~50号为左联33~43号坝段。可以看出:除了不同类型坝段的交接坝段测点外,同一类型坝段测点的相似系数较为接近,表现为较为稳定的变化趋势。同类型坝段中,25号测点与周围其他同类坝段测点的相似系数差距明显,该坝段为坝顶18号坝段,是纵向围堰与坝体的交叉坝段;38号测点与周围其他同类坝段测点的相似系数差距明显,主要是由该测点数据异常引起的。左联坝段的相似系数浮动较大,需对此区间坝段测点进行重点关注。由此可见,通过云相似系数的方法可以快速确定复杂坝型多个坝段中需要重点关注的坝段。
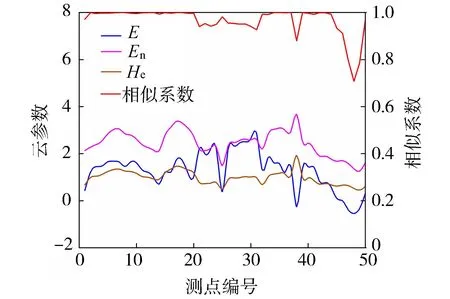
图1 坝顶垂直位移测点的云参数和相似系数
3.2 重点坝段数据分析
根据上节分析,左联坝段测点数据呈现不稳定变化趋势,进一步对左联坝段11个测点进行重点分析。首先观察其垂直位移过程线,如图2所示。

图2 左联坝段测点垂直位移过程线
可以看出:①测点的垂直位移变化总体平稳,主要受温度影响呈现周期性变化,气温降低,坝顶位移增加(坝顶下沉);气温升高,坝顶位移减少(坝顶上抬),且温度对垂直位移的影响呈现一定的滞后性,垂直位移整体有逐渐增大趋势。②2017年库水位抬升期间,坝段各测点垂直位移有所增加,总体与往年同时期变化规律保持一致,因为更多是受温度影响,水位抬升对坝顶垂直位移影响不大。③47~49号测点整体位移变化规律与其他测点保持一致,但其位移值及变幅相对较小,这也验证了利用云模型可快速找出与大坝整体位移状态存在差异的点的结论,说明了云相似方法发现异常测点的有效性。
3.3 多测点分组
通过3.2节的分析验证了本文提出的方法的可行性,因此可以对3.1节得到的不同测点进行与混凝土总体变形性态的关联分析。由于坝体运行整体处于正常状态,因此正常点位占据多数,少数的测点存在异常数据变化序列,需要对其进行重点关注。根据所有测点的相似系数,使用SPSS软件的K均值聚类将测点分为两组:正常测点和异常测点,对应的测点个数分别为47个和3个,除正常测点外,异常测点为47、48、49。由于38测点存在明显的拐点,因此将该点也进行分析,4个异常测点的相似度和相似系数如表 1所示,并增加相似度最高的测点37作为对比参照。

表1 测点分组后的异常测点
通过分析可以发现,38号测点存在明显的数据异常,其他几个查找到的异常测点数据变化规律整体表现较好,但与表征大坝整体位移变化规律相似性最高的37测点数据变化规律有所差别,表现为其位移极值及变幅的差异。
可以看出,通过多测点相似系数聚类分析对测点进行分组能够有效找出数据变化规律与大坝整体数据变化规律异常的测点,在证明了数据分组有效性的同时,也为工程管理人员关注重点测点提供了数据支撑,管理人员可以对那些反映坝体正常运行性态的多数测点和对坝体运行性态起到关键作用的少数测点给予不同的关注。因此通过测点之间的相似系数对测点进行分组的方法能够实现测点分级管理,在识别大坝异常点位的同时提高数据分析的效率。
4 结 语
云模型可以反映自然语言中概念的不确定性,不但能够通过经典的概率论和模糊数学对其作出解释,并且能够很好地反映随机性和模糊性之间的关联,且在大数据的处理上具有很好的效果。本文针对混凝土坝变形监测数据分析中测点多,分析数据量大,单测点分析难以反映与大坝整体变形性态关联的不足,引入云模型进行混凝土坝变形监测数据的关联分析。通过将每个测点视为一个云,采用云计算方法对监测数据的云参数和云特征进行分析,利用云模型定性定量转换的双向认知模型的特点,将给定的数据样本集合转换成多个可以用云来表征的定性概念,实现定量数据到定性概念的转化。将混凝土坝每个测点的监测数据视为一个云,测值视为云滴,通过逆向云算法计算出不同变形测点的期望、熵、超熵等云模型参数,进一步使用余弦相似度方法计算大坝不同测点之间的云相似度并归一化处理得到云相似系数,表明云相似计算可以表征测点之间的相似程度,验证了云相似系数表征测点之间相似性的可行性;同时根据相似度的聚类特征对测点进行分组整编分析,可以实现大坝变形性态的关联分析,对于迅速发现复杂坝型中运行状态异常坝段具有良好的效果,大幅度提高了多测点海量监测数据的分析效率。

