喀斯特地区双荚决明单根抗拉变形特性

潘 露， 张乔艳， 郭 欢， 唐丽霞†

(1.贵州大学林学院，550025，贵阳；2.贵州省国有扎佐林场，550025，贵阳)

植物根系在加强边坡稳定、增强土体强度等方面有显著作用，能有效地防控水土流失、浅层滑坡及泥石流等地质灾害[1-5]。植物根系的固土作用主要体现为以深粗根的锚固、浅细根的加筋以及植物蒸腾降低坡体孔隙水压力来增加斜坡的稳定[4,6]；而植物的抗拉特性是决定根系护坡的关键，在含根土体受到剪切作用时，根系所受的剪切应力因变形拉直转化为拉应力，故单根抗拉是研究根系固土的基础[7-8]。

国内外学者对植物根系抗拉力学特性开展大量的研究。Baets等[9]对地中海地区25种植物根系进行单根拉伸试验得到植物单根抗拉力随根径增加呈增加趋势，且单根抗拉强度与根径为负相关，其函数关系受植物的种类影响。吕春娟等[10]和刘亚斌等[8]对不同植物根系的单根抗拉研究也得到相似的结果。上述研究主要探究植物种类以及根系直径对单根抗拉特性的影响。为进一步解释根径与抗拉力及抗拉强度的关系，李可等[11]和张乔艳等[12]通过拉伸断面电镜扫描，得出根系的微观结构是决定根系力学特性的主导因素。李宁[13]和Sluiter等[14]从根系化学成分方面探讨木质素和纤维素对力学特性的影响。吕春娟等[15]和张乔艳等[16]对不同植物根系的化学成分及力学性能进行测定，结果表明根系化学成分对其力学性能有影响。李长暄等[17]结合应力应变曲线特征对蒙古栎(Quercusmongolica)的抗拉力学特性进行研究，得出不同径级的应力应变曲线均为单峰型，表现出弹塑性材料特征，这与王萍花等[7]对乔木单根拉伸的应力应变曲线研究结果一致。单根的应力应变曲线是揭示根系抗拉过程的基础，不同树种、不同年龄、不同根长、不同根径以及不同拉伸速率都可能会影响其本构关系[18]。

以上研究从不同角度解析根系抗拉力学特征及其影响因素，为植物根系固土护坡提供一定的理论支撑，贵州省是我国西南喀斯特区的核心，区内基础设施的建设导致形成大量裸露边坡，土少石多、蓄水难等现状使得生态修复难度大，植物护坡对该地区的生态修复与重建起重要作用。笔者以适应性广、萌芽能力强、耐干旱瘠薄的双荚决明(Cassiabicapsularis)根系为研究对象，通过单根拉伸试验测定不同根长和拉伸速率对其单根抗拉力、抗拉强度以及应力应变曲线的变化特征，以期探究喀斯特石质边坡上双荚决明单根受力变形特性，为喀斯特地区边坡根系固土机理研究、生态恢复和防治滑坡提供理论研究价值和实际指导意义。

1 研究区概况

研究区位于贵州省贵阳市花溪区，地理位置为E 106°27′～106°52′，N 26°11′～26°34′，海拔为1 030～1 326 m，该区属亚热带季风湿润气候，年均降水量1 229 mm，年平均气温15 ℃[19]。区内土壤主要为酸性黄壤土和石灰土，土壤分布不均，土被破碎。喀斯特区边坡土少石多，生态修复中常以土石混合堆积为主，辅以铁丝网格稳定后，以种植灌木来达到固土护坡目的。植物根系侧根在表层土壤中水平分布，主根穿透混合土石，沿岩石缝隙扎到坡体深处以达到边坡防护。边坡防护多为喜钙和石生植物，主要有火棘(Pyracanthafortuneana)，野蔷薇(Rosamultiflora)，荚蒾(Viburnumdilatatum)，花椒(Zanthoxylumbungeanum)，多花木蓝(Indigoferaamblyantha)，双荚决明(Cassiabicapsularis)等[20]。

2 材料与方法

2.1 根系采集及制备

于2019年7月进行根系的采集与制备，以撒种生长5 a，长势一致，无病虫害的双荚决明作为实验株。采用全挖法获取根系，清除根系表面杂质后，将根系制成标距分别为50、100 mm的试验样(根段总长分别为110和160 mm，两端各留30 mm自由端用于与夹具接触)并置于自封袋封袋保存，进行室内拉伸试验。当天未能完成测定的根系，放于4 ℃冰箱保持根系的鲜活，所有根系于7 d内完成实验。

2.2 根系抗拉力学特性的测定

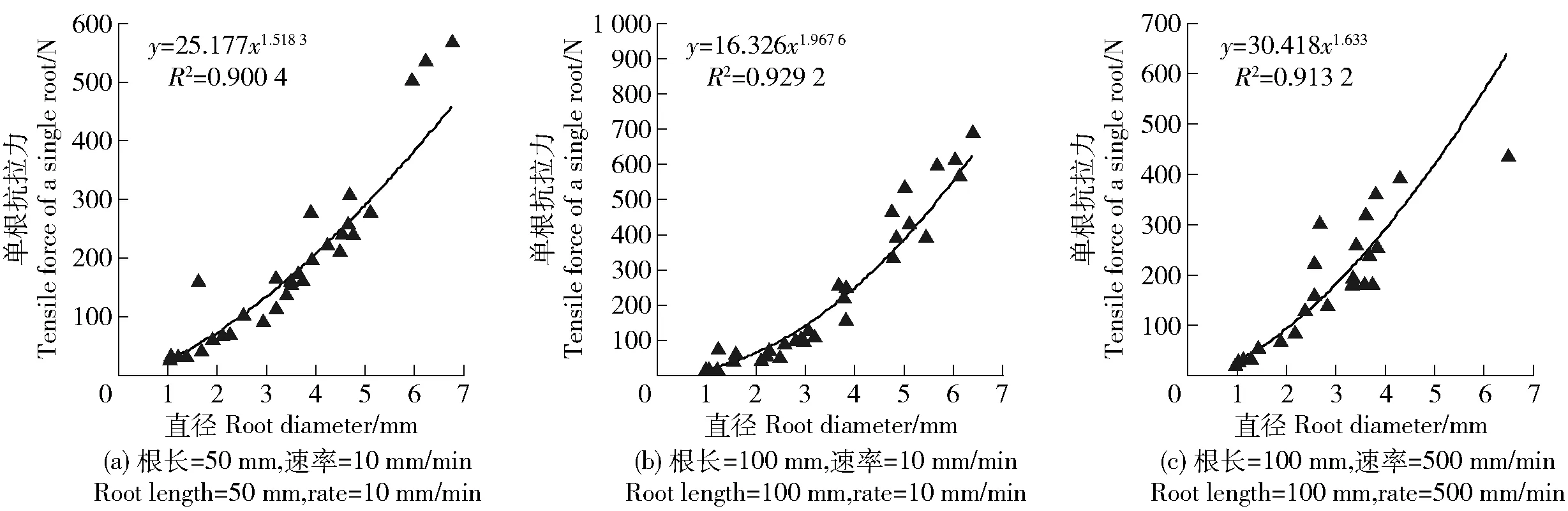
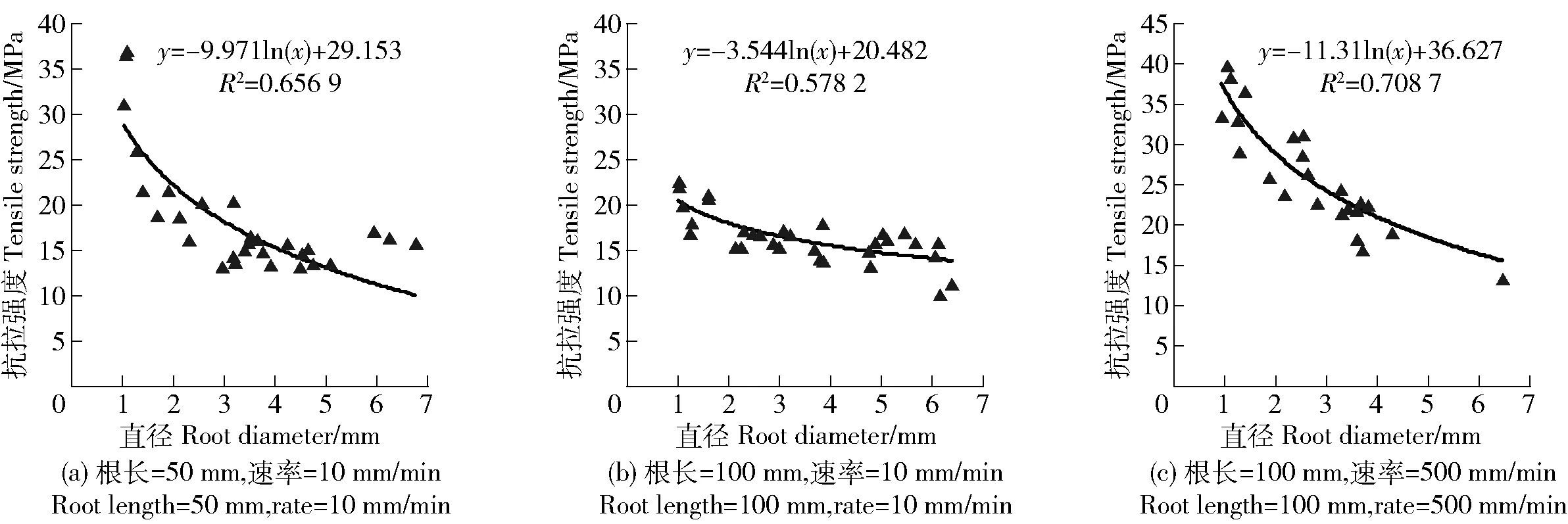
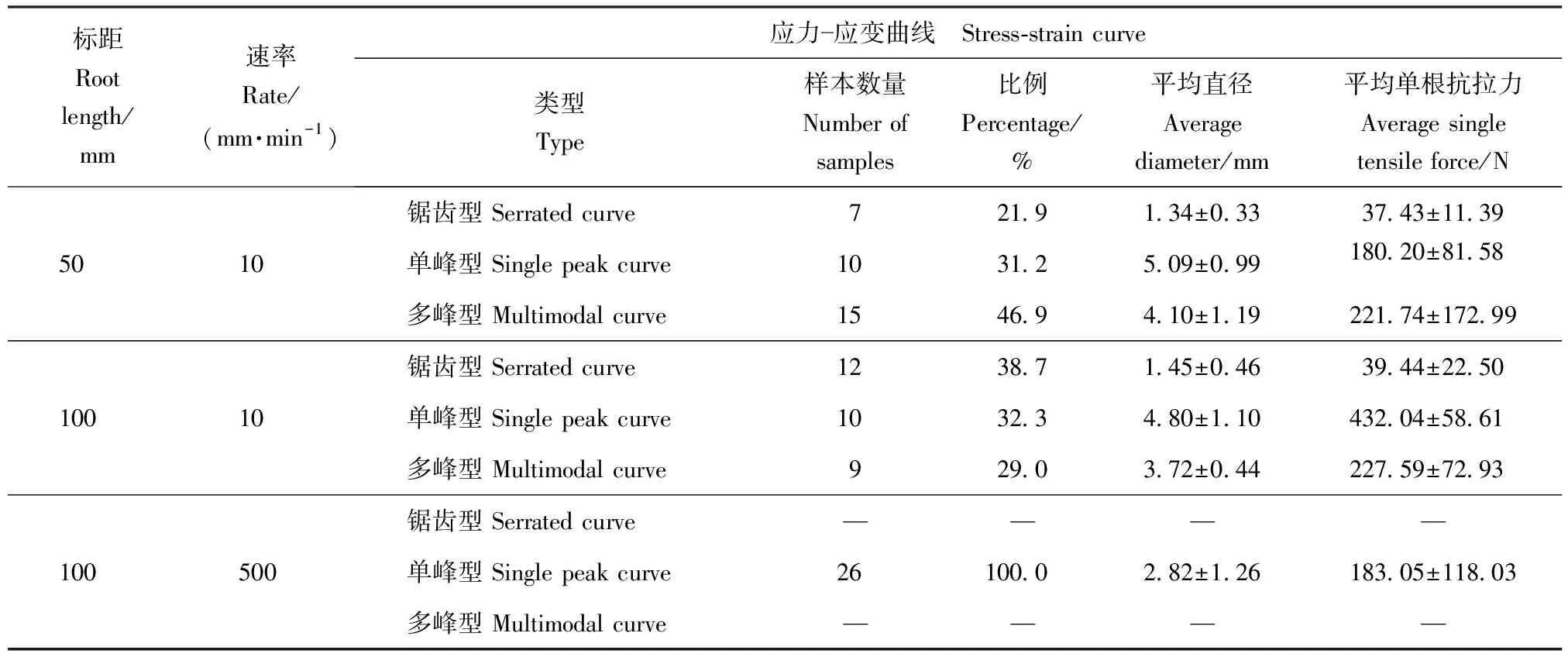
用电子游标卡尺分别测量根段标距两端和中间的直径，取其平均值作为该根段的直径。根据平均直径D将实验根分为5个径级，分别为径级Ⅰ(0.5

实验仪器采用济南耐尔试验机DWD-10，最大量程为10 kN，速度0.001～500 mm/min。为减少试验误差，根系滑出夹具或被夹断均视为无效试验，当根系断裂处明显远离夹具时为成功试验。试验总根数为210根，有效根系为89根，成功率为42.38%。

在研究根长对根系变形的影响时，拉伸速率选用10 mm/min，标距分别为50、100 mm。预实验表明，标距小于50 mm的根段很难固定在万能试验机上，而大于100 mm的顺直根段很少，故选用50和100 mm这2个标距。为模拟在自然状态下滑坡缓慢发生和大风条件下的滑坡发生[21]，在研究拉伸速率对根系变形的影响时，标距选用100 mm，拉伸速率分别为10、500 mm/min。

2.3 数据处理

林木根系的抗拉强度是指根系在外力拉伸下抵抗破断的能力[9]。公式如下：

P=4Fmax/πD2；

(1)

σ=4F/πD2；

(2)

ε=ΔL/L。

(3)

式中：P为根系抗拉强度，MPa；Fmax为根系极限抗拉力，N；F为实时拉力，N；σ为应力，MPa；D为根系平均直径，mm，由于在实验过程中无法测量根系断裂时的直径，所以认为实验过程中直径没有变化；ε为纵向线应变即延伸率；ΔL为根系的延长量，mm；L为两夹具之间受到拉伸作用的根长，mm，即为标距。数理统计方法为卡方独立性检验。

3 结果与分析

3.1 单根抗拉力学特性

3.1.1 不同根长、拉伸速率下单根抗拉力与根径的关系 由图1a和1b可见不同根长下双荚决明单根抗拉力与直径均呈幂函数关系增长，根长对单根抗拉力与根径之间的关系影响不大。由图1可知不同拉伸速率下双荚决明单根抗拉力与直径之间均呈幂函数关系增大，表明拉伸速率对单根抗拉力与根径之间关系影响不大。

图1 双荚决明单根抗拉力与根径的关系Fig.1 Relationship between tensile force of a single root and root diameter of Cassia bicapsularis

不同条件下最大抗拉力与直径之间的函数关系式不同。根长50 mm，拉伸速率10 mm/min；根长100 mm，拉伸速率10 mm/min和根长100 mm，拉伸速率500 mm/min条件下单根抗拉力与直径之间函数关系式分别为y=25.177x1.518 3(R2=0.900 4)；y=16.326x1.967 6(R2=0.929 2)；y=30.418x1.633(R2=0.913 2)。

3.1.2 不同根长、拉伸速率下单根抗拉强度与根径的关系 图2为双荚决明单根抗拉强度与根径之间的关系曲线，可见不同根长条件下单根抗拉强度与根径之间均呈对数函数关系减小，对比图2b及图2c可得不同拉伸速率下单根抗拉强度与根径之间均呈对数函数关系减小，表明根长和拉伸速率对单根抗拉强度与根径之间关系影响不大。

图2 双荚决明单根抗拉强度与根径的关系Fig.2 Relationship between tensile strength of a single root and root diameter of Cassia bicapsularis

3.2 应力-应变曲线

应力应变曲线可表现出多个拉伸力学性能指标，如弹性模量、极限延伸率、抗拉强度等，此外，应变状态还能反映单根受力时的变形情况。本研究结果表明，双荚决明单根拉伸应力应变曲线多样，主要表现为锯齿型、单峰型和多峰型3种(图3)。

图3 双荚决明单根应力应变曲线类型Fig.3 Types of stress-strain curve of a single root of Cassia bicapsularis

图3a为锯齿型曲线，在受力初期，OA段应力随应变呈直线增加，锯齿波动不明显，单根为弹性变形，随着拉力持续增加，曲线斜率发生变化，AB段锯齿型逐渐变明显，即出现屈服阶段，小范围内应变增加而应力没有变化，单根变形为弹塑性变形。当应力达到最大值时，根系断裂，应变达到最大值。

图3b为单峰型曲线， OA段为受力初期，应力随应变呈线性递增，此阶段为弹性变形阶段。AB段为单根受力中期，应力应变曲线呈非线性，单根进入弹塑性变形阶段，单根在力的作用下开始屈服。经过屈服阶段后， BC段为受力后期，单根进入硬化阶段，应力随应变增大而增大，直至达到应力峰值，单根断裂，应力迅速下降为0，此阶段为塑性变形。

图3c为多峰型曲线， OA段为弹性变形阶段，应力与应变关系曲线近似直线。AB段为屈服阶段，应力应变曲线呈非线性，撤去拉伸力后，单根不能完全恢复至拉伸前的状态，而保留一部分残余变形。BC段为硬化阶段，应力与应变之间增长关系近似线性增长，应力增至C点后根皮撕裂，应力下降。CD段为根皮撕裂阶段，应变增加，应力呈多峰型上下波动，根皮断裂后中柱继续抵抗变形，故D点处应力表现为增大至最后一个峰值后迅速下降至0。

3.3 不同根长、不同速率对应力应变曲线的影响

通过在不同拉伸速率下对不同根长的双荚决明根系进行单根拉伸试验，将应力应变曲线进行分类汇总得到表1。

表1 双荚决明应力应变曲线类型汇总表Tab.1 Summary of the types of stress and strain curves of Cassia bicapsularis

3.3.1 不同根长下的应力应变曲线 由表1可见，双荚决明根系在拉伸速率为10 mm/min，根长为50和100 mm条件下应力应变曲线多样，锯齿型、单峰型和多峰型均有，且不同根长下各类型占比不同。根长为50 mm条件下多峰型曲线占比最大，且其对应的根径范围较广。根长为100 mm条件下各类型曲线占比相差不大。值得注意的是，2种根长条件下锯齿型曲线均为根径小于2 mm的单根应力应变曲线，说明直径较小的根系对外界拉力的缓冲能力更强。对不同根长的实验结果进行卡方独立性检验，结果表明，根长与应力应变曲线类型没有显著的相关性，χ2=2.801，P=0.247>0.05，接受原假设，即根长对应力应变曲线无显著影响。

3.3.2 不同速率下的应力应变曲线 由表1可见，在根长均为100 mm，拉伸速率为10 mm/min条件下，应力应变曲线类型多样且各类型占比均匀。拉伸速率为500 mm/min时所有应力应变曲线均为单峰型。对2种拉伸速率下的实验结果进行卡方独立性检验，结果表明，拉伸速率与应力应变曲线类型间有显著的相关性，χ2=27.887，P=0.00<0.05，拒绝原假设，即拉伸速率对应力应变曲线类型有显著影响。

4 讨论

单根的应力应变曲线是揭示根系抗拉过程的基础，曲线反映单根受拉力过程中的变形特性。笔者通过在不同拉伸速率下对不同根长的双荚决明进行单根拉伸实验，试图探究喀斯特地区双荚决明单根抗拉变形特性。结果表明：

1)双荚决明单根抗拉力随直径增大而呈幂函数递增，单根抗拉强度随直径增大呈对数函数递减。这与前人对其他植物单根拉伸的研究结果相近，李可等[11]对早熟禾和柠条锦鸡儿的研究结果表明2种植物根系抗拉力与根径间均呈幂函数关系增长，抗拉强度随根径增加而递减，2种植物递减关系不同。吕春娟等[10]对5种乔木抗拉特性进行研究，表明5种乔木根系极限抗拉力与直径之间为幂函数关系，油松和白桦根系抗拉强度随着直径增大以幂函数递减，蒙古栎、落叶松和榆树根系的单根抗拉强度随根径增大呈对数函数关系递减。

2)喀斯特地区双荚决明单根抗拉变形多样且过程复杂，根据应力应变曲线形态可将曲线分为3种类型，锯齿型、单峰型和多峰型。锯齿型主要包括弹性阶段和屈服阶段2个阶段，对应的变形特征为弹性变形和弹塑性变形，与软钢受拉的应力应变曲线有所不同，锯齿型曲线没有强化阶段和局部颈缩阶段。单峰型曲线表现为弹塑性材料受拉变形过程，主要包括弹性阶段、屈服阶段和强化阶段，单根形态变化为弹性变形后到弹塑性变形，再到塑性变形直至断裂。多峰型主要包括弹性阶段、屈服阶段、强化阶段和局部颈缩阶段，由于根系属于高分子材料，材质具有不均匀性，在局部颈缩阶段变形体现为根皮撕裂，单根形态变化过程包括弹性变形、弹塑性变形、塑性变形、根皮撕裂和完全断裂。李长暄等[17]对蒙古栎的单根拉伸应力应变曲线研究结果表明各径级应力应变曲线均为单峰型，这与本研究结果有所差异，这可能是树种差异造成的。

3)对应力应变曲线类型进行统计分析，在速率为10 mm/min，根长为50和100 mm条件下，3种应力应变曲线均有出现，根长对应力应变曲线类型无显著影响。在根长为100 mm，速率为500 mm/min条件下，应力应变曲线均为单峰型，拉伸速率对应力应变曲线类型有影响，说明在拉伸过程中，拉伸速率对单根变形特征有影响，其原因可能是在较快的速率下，纤维束来不及发挥自身的抗拉特性，根系经硬化阶段后迅速断裂。锯齿型曲线均为根径<2 mm的单根，这与细根的生物学特性有关，根径<2 mm的单根木质部发育不成熟，纤维素含量高，各组织分化不明显，根皮和内部组织间黏附力强，故没有强化阶段和根皮撕裂阶段。这种非光滑的曲线特征与钢筋受拉的应力应变曲线完全不同，说明细根在拉伸过程中对外界拉力具有较强的缓冲能力。这与王萍花等[7]、ZHANG[22]的研究结果一致。

5 结论

1)喀斯特地区双荚决明单根抗拉力与根径之间呈幂函数关系递增，抗拉强度与根径之间呈对数函数关系递减，其抗拉特性与非喀斯特地区植物一致。

2)双荚决明单根受拉变形多样且过程复杂，应力应变曲线可分为锯齿型、单峰型和多峰型，单根以弹性变形、弹塑性变形以及根皮撕裂等变形方式来抵抗破坏，具有较强的变形能力。且变形方式与根径有关，细根仅能发生弹性变形和弹塑性变形。

3)根长对应力应变曲线类型没有显著影响。拉伸速率对应力应变曲线影响较大，拉伸速率为500 mm/min时，应力应变曲线均为单峰型。在较快速率下，根系更容易被破坏。直径较小的根对外界拉力具有较强的缓冲能力。