一种基于步长指数递减策略的果蝇优化算法

秋兴国，黄润青

（西安科技大学计算机科学与技术学院，陕西西安 710054）

果蝇优化算法是潘文超[1]于2011 年提出的一种新型演化式群体优化算法[2]，该算法模型的构建是基于果蝇觅食行为的仿生学原理[3]，目的是寻找全局最优值，与其他算法相比具有参数少、易于实现和局部搜索能力强[4]等优点，但它同时具有收敛速度慢、不够稳定、易陷入局部最优等局限性[5]。为提高传统果蝇算法的性能，文献[6]提出了一种融合变异机制的果蝇优化算法，通过使位于种群中心的个体进行变异操作来避免算法易陷入局部极优值的情况；文献[7]提出的果蝇优化算法融合了模拟退火的思想，使用非均匀变异的思想优化果蝇迭代步长，使算法收敛速度和精度得到了提高；文献[8]将莱维飞行和反向学习引入果蝇算法中，通过对果蝇个体进行位置更新来控制算法的收敛速度和精度。

文中提出一种基于t分布及自适应步长策略的果蝇优化算法(TEFOA)，该算法从种群位置初始化、果蝇位置更新两个方面来进行优化。通过t分布对果蝇位置更新时进行位置扰动，使种群具有更加随机的特点，引入指数递减步长调整因子，优化了原有算法的位置更新方式。对5 个经典性能函数进行仿真测试，结果表明，提出的果蝇优化算法有较好的收敛速度收敛精度，降低了算法陷入局部极值的可能性。

1 果蝇算法基本介绍

果蝇优化算法是一种演化式群智能优化算法，是基于果蝇觅食行为提出的。果蝇在嗅觉和视觉[9]上的敏感性优于其他物种。在觅食过程中，每个果蝇个体携带有食物味道浓度，在算法中将果蝇个体与原点位置距离的倒数作为味道浓度判定的方法[10]，果蝇群体中所有个体朝味道浓度最优的果蝇个体位置飞去[11]，该味道浓度最优的果蝇个体位置作为下一次迭代寻优过程中果蝇种群的初始位置，通过数次迭代，不断更新果蝇群体的最优位置，直到得出最优解或达到最大迭代次数[12]。图1 显示了果蝇搜寻食物的逻辑迭代过程。

图1 果蝇群体进化图

根据果蝇觅食过程中的行为特点，将标准的果蝇优化算法归纳为以下步骤[13]：

1）初始化相关参数，主要包括果蝇种群规模(Sizepop)、群体最大迭代次数(Maxgen)、果蝇个体初始位置X-axis、Y-axis，并进行群体位置初始化，其中rand()表示[0,1]间的随机数。

2）确定初始果蝇群体中果蝇个体位置和方向。RValue为果蝇随机搜索距离和方向的随机数。

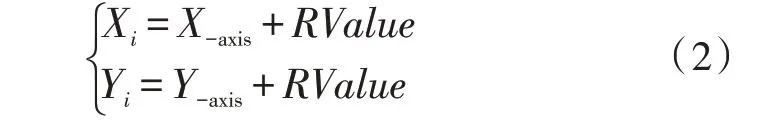
3）利用每个果蝇个体位置坐标与原点的距离Di来计算其味道浓度判定值Si，Si为距离Di的倒数。

4）将味道浓度判定值Si代入适应度函数判定函数[14](或称为适应度函数，Fitness function)，该函数是为了计算该种群中果蝇个体的味道浓度Smell(i)。

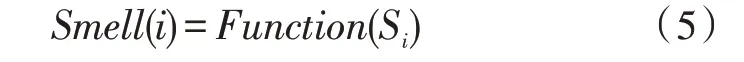
5）找出种群当前味道浓度最优的果蝇个体位置，记录其坐标和味道浓度值。

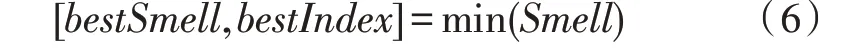
6）记录最优味道浓度值及对应的横纵坐标，此时群体果蝇根据视觉向最优个体位置飞去，形成新的果蝇群体。

7）迭代寻优阶段，重复执行步骤2)～步骤5)，判断当前迭代次数是否小于最大迭代次数，当前味道浓度是否优于所记录的最优味道浓度，若成立，执行步骤6)。

2 改进的FOA算法(TEFOA)

2.1 指数递减步长

搜索步长是决定FOA 算法搜索能力的关键因素。由指数函数确定的自适应步长在初期迭代搜索时，可在较大范围内展开全局搜索，这有利于跳出局部最优解[15]，加快算法的收敛速度，降低运行时间；随着迭代次数的增加，在算法运行后期，由于已经步入了有潜力的搜索区域，只需要在区域内进行局部搜索，即设置较小的搜索步长在当前搜索区域进行精细搜索[16]。受文献[9]的启发，用指数递减策略对果蝇算法进行优化。所使用的指数递减策略表达式为：

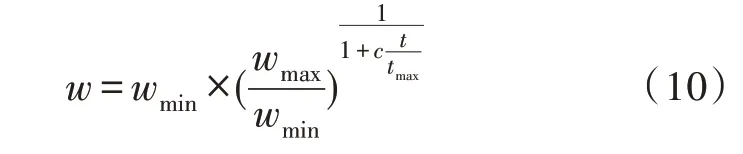
其中，wmax、wmin分别表示w的最大值和最小值，取wmax=1，wmin=0.4[13]；t表示当前迭代次数；tmax为最大迭代次数；参数c取值与文献[9]保持一致，即c=10。该函数图像如图2 所示，在果蝇算法迭代寻优初期，w随迭代次数的增加以较快的速率下降，可使果蝇个体在初期能够保持一个较大的搜索步长。该算法搜索能力较强，为避免出现算法陷入局部极优值的情况[17]。在算法迭代寻优后期，当迭代次数逐渐增加时，w以非线性的动态逐步减小，搜索步长变小，可以进行精细搜索。这不仅能够避免因步长较大而跳过最优解的可能性[18]，而且还提高了算法后期的收敛精度和时间效率[19]。

图2 指数递减因子的变化曲线

指数递减结合果蝇算法的具体公式下，其中t(Iteration)为变异策略。

2.2 t变异策略

1908 年，威廉·戈塞[20]首先推导出t分布。t分布图像形态与n(自由度)有关。自由度越小，t分布的曲线愈平坦，曲线中间越低，曲线双侧尾部越高。自由度n=1 时，t分布的曲线为柯西分布曲线，即t(n=1)=C(0,1)，C(0,1)为柯西分布；自由度越大，t分布的曲线越接近正态分布曲线[21]；自由度n→∞时，t分布的曲线近似为高斯分布曲线[22]，即t(n→∞)→N(0,1)，其中N(0,1)为高斯分布。即t分布的两个特殊情况[23]是柯西分布和高斯分布。t分布的自由度分布曲线如图3所示，在算法优化中，t分布自由度的取值为当前迭代次数。

图3 t分布曲线图

3 仿真实验及结果分析

3.1 测试函数验证

为了检验算法的有效性，选取了5 个经典性能测试函数对标准果蝇算法和文中优化算法在相同环境下进行Matlab 仿真实验对比(求最小值)，所选函数均有不同特性，使用这些函数进行测试所得的实验结果可以全面地反映算法的性能，更具有说服力。

实验中所采用的经典测试函数如表1 所示。

3.2 固定迭代次数下实验仿真分析

在测试函数过程中，借助Matlab 2016a 平台，设置迭代次数为1 500 次，种群规模为20，算法独立重复实验50 次。为了使测试结果更具有说服力，选取FOA、LGMS-FOA[24]、TEFOA 这3 种算法进行同条件测试，记录实验过程中的平均值、标准差和测试函数最优值作为评价标准。实验中所采用的标准测试函数如表1 所示，实验结果如表2 所示，其中Mean 表示函数的平均值，Std 表示函数的标准差，Best 表示函数可达到的最优值，并绘制迭代次数增加时适应度值的变化曲线。

表1 测试函数

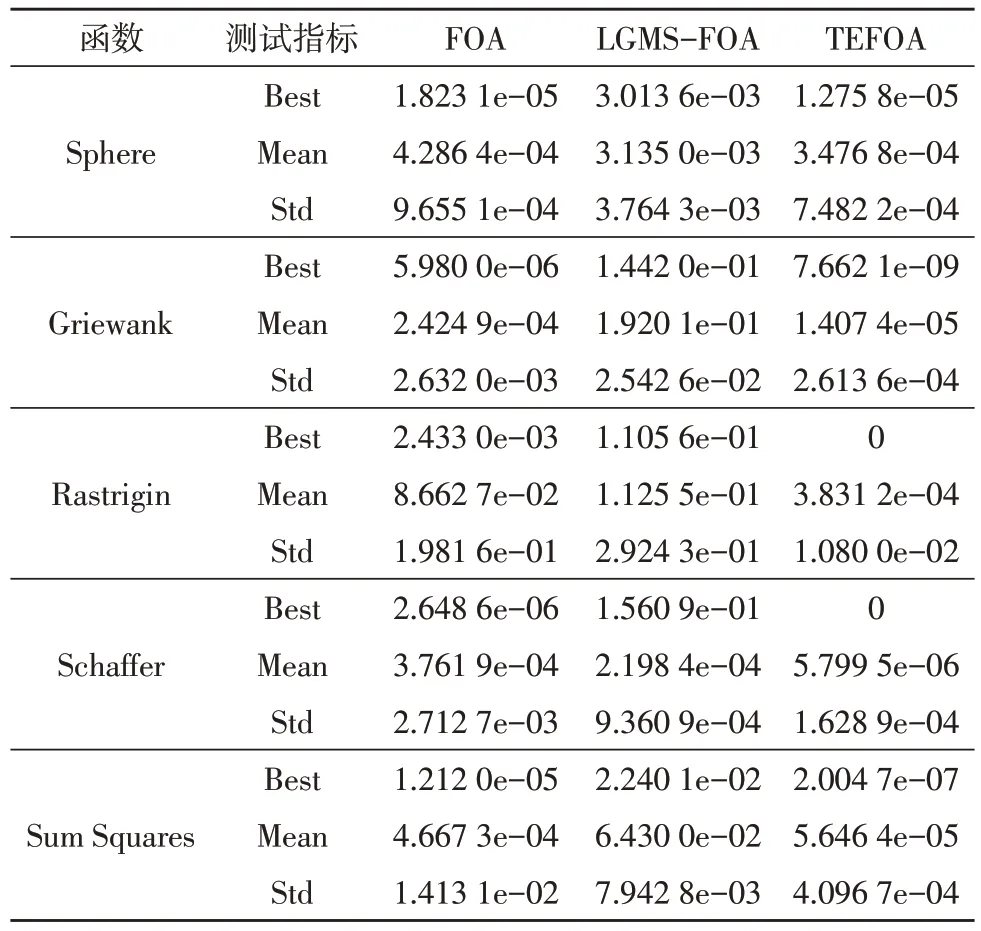
表2 测试结果表

测试函数的变化曲线如图4～8 所示。

图4 Sphere函数变化曲线

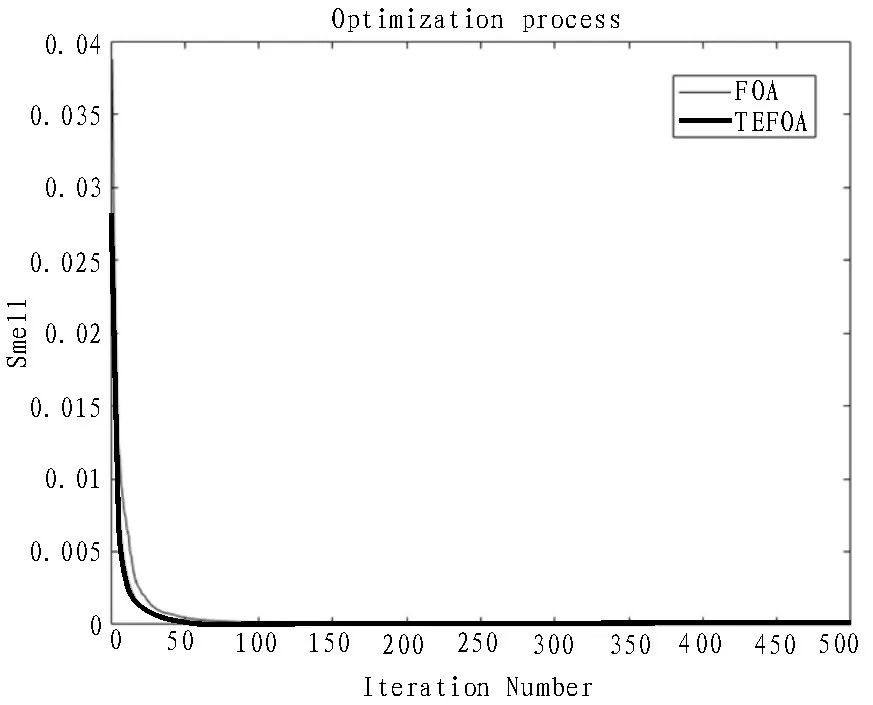
图5 Griewank函数变化曲线

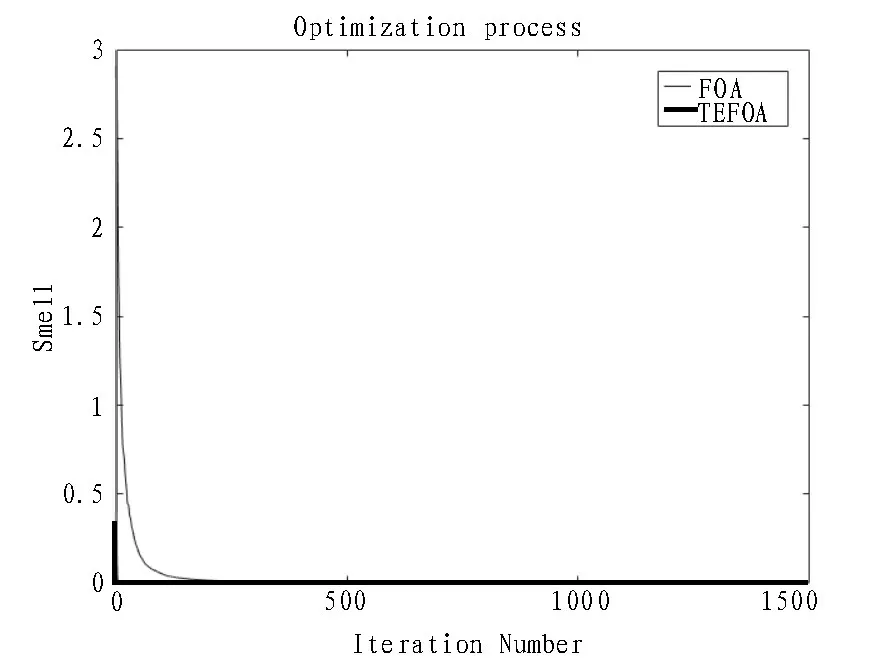
图6 Rastrigin函数变化曲线

4 结束语

图7 Schaffer函数变化曲线

图8 Sum Squares函数变化曲线

通过对实验结果进行分析可知，尽管函数对于不同的算法有着不同的寻优精度，但在5 种标准函数的测试中，文中优化算法比标准FOA 算法的运算精度均有不同程度的提高。所以，提出的TEFOA 算法优于传统的FOA 算法，尤其是在Rastrigin 和Schaffer 两个测试函数上表现优异，在迭代过程中训练得出的最优值均可达到函数本身的最优值；另外，从适应度值的变化曲线可以看出，平均迭代不到500次就可获得最优值，TEFOA 算法的收敛速度优于传统的FOA 算法，收敛速度得到了较大的提高。这充分说明了文中的改进算法具有更高的收敛精度、更优的搜索能力和更快的收敛速度，在一定程度上也可以避免局部最优[25-26]。

FOA 算法是近年来提出的种群智能优化算法，但传统的果蝇算法存在着局限性和不足之处，如难以跳出局部最优值、收敛缓慢、精确度不高等。文中考虑到这些方面的问题，在优化算法中对果蝇算法的移动步长部分作了指数调整策略，即在迭代的初期阶段保留了算法较大的搜索步长，也保留了迭代后期算法的精细搜索能力；并在果蝇位置更新时添加扰动策略，避免算法难以跳出局部最优解。经Matlab 平台对标准函数进行测试实验，结果表明，文中的算法改进使得算法易陷入局部最优和收敛速度慢的不足得到了优化，并提高了求解效率。接下来的任务是将改进算法应用于实际问题，验证解决实际问题的能力。