有限元分割的共轭方向优化算法

李有堂，梅鹤龄

（兰州理工大学机电工程学院，甘肃兰州 730050）

随着科技的进步和发展，精密、超精密设备与加工技术标志着一个国家制造领域的尖端技术水平，已成为当今世界各国进行科技竞争的一个重要手段[1]。计算机的快速发展以及互联网的迅速普及，信息在互联网上爆发式增长，文本、图像、音频、视频等的发展导致表达数据需要更高的维度[2]。这些改变无疑对数据类问题的处理提出了更高的要求，不仅对数据的处理效率和便捷度提出了要求，对估算计算的数值要求有更高的准确度(误差降低到满足要求的范围内)。

无约束优化算法作为最优化方法的基础，在交通运输、工农业生产、金融、贸易等众多领域有着广泛应用。伴随着信息技术的飞速发展,变量维数的剧增以及结构复杂性的增强，能有效求解大规模无约束优化问题的算法显得尤为重要[3]。在优化算法的发展过程中，1964 年由鲍威尔提出的共轭方向法(Conjugate Direction Method)起到了举足轻重的作用。共轭方向法可以在有限步数内找到二次函数的极值点和极值，并且对非二次函数只要具有连续二阶导数，也是一种有效的算法[4]。但是，共轭方向法的主要缺点是更换方向后所产生的n个矢量有可能是近似线性相关的，即这些矢量接近于平行。这样就会出现维度退化现象，导致只能找到局部最优解，有可能使真正的全局最优解漏掉[5]。

针对共轭方向法的该缺陷，在实际工程应用中通过与其他算法组合或对算法进行改进以提高解决问题的准确度[6]。例如：在一些优化问题中，当粒子群算法(PSO)经过一段时间的迭代后，会陷入局部最优解的局部极小值中，这时采用共轭方向法，以局部最优解作为初始猜测，将高维函数优化问题转化为低维函数优化问题，帮助粒子群算法克服局部极小问题[7]；对于移动机器人全局路径规划问题，先用共轭方向法搜索局部最优解，再用改进模拟退火算法(SAA)跳出局部最优解，依此更新温度值，如此反复操作，直至找到全局最优解[8]；针对遗传模拟退火算法的局部搜索能力不足，并且有可能早熟和遗失最优解的问题，提出一种将遗传模拟退火算法和共轭方向法相结合的混合遗传模拟退火算法[9]；还有对多维优化问题的求解，通过对Powell 机械优化方法的改进，提出了方向组不降维的构造共轭方向法[10]。

随着科技的发展，基础科学也在进步，对于不同的优化问题采用不同的优化算法，一些有约束问题往往采用无约束优化算法进行求解。通过以上综合分析，提出了一种求解有约束优化问题的有限元分割共轭方向法，可以杜绝所求优化解为局部最优解的产生。

1 共轭方向法

共轭方向法是利用共轭方向作为搜索方向的无约束极小算法，而且已证明这类算法应用于具有正定Hesse 矩阵的二次函数时，最多n次迭代即可达到极小点。这类算法具有有限收敛性，形成共轭方向的方法很多，每一种不同的构造共轭方向的方法形成一种具体的共轭方向法，因而共轭方向法是一大类算法[4]。

1.1 共轭方向法基本原理

m个n维向量S1,S2,…,Sm，满足=0，i≠j且A正定，则这m个向量一定是线性无关的。在n维空间中的任意向量，均可以用n个线性无关的n维向量表示。

设目标函数为：

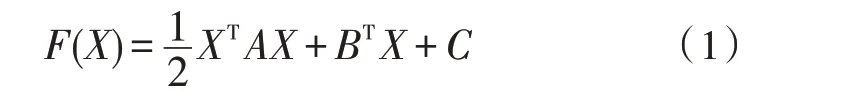
它的极小点为X*，初始点X0,S0,S1,S2,…,Sn-1为关于A的n个共轭向量，则有：

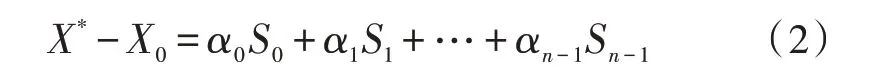
将式（2）写成差分格式：

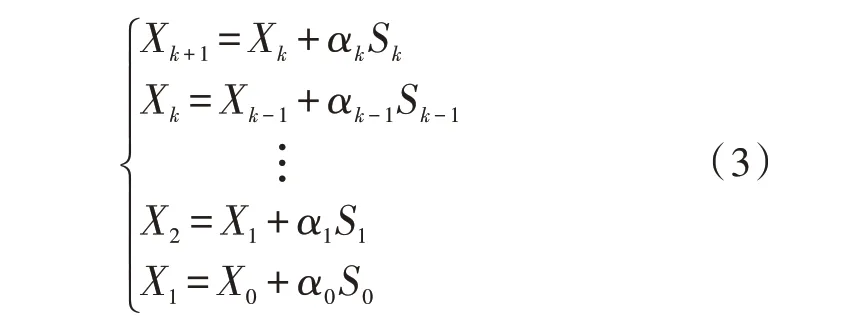
式（3）表明，经(k+1)次迭代后，Xk+1→X*,Xk+1为目标函数沿Sk方向的一个极小点。则：

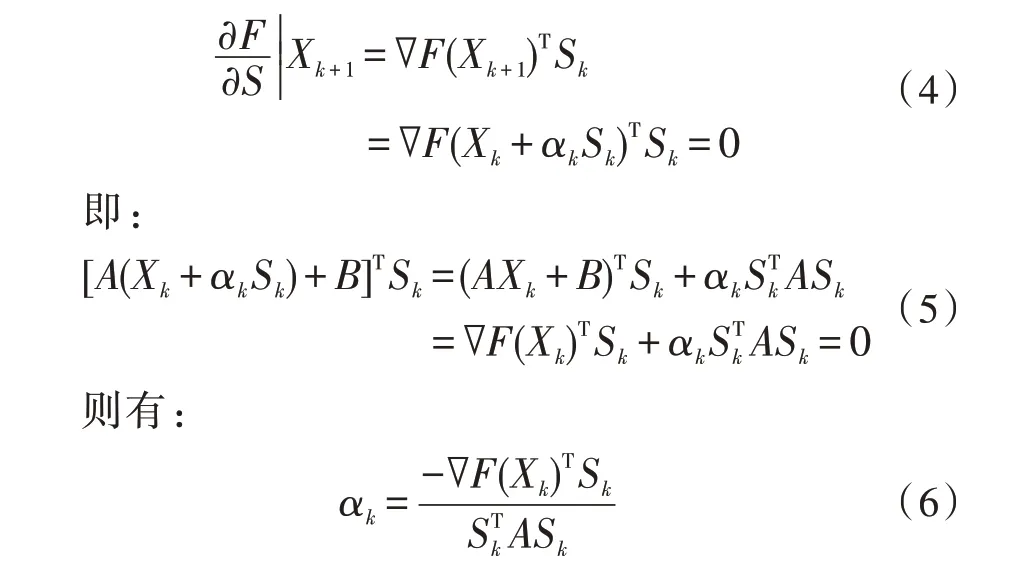
对于二元二次函数只需进行两次直线搜索就可以求到极小值点。

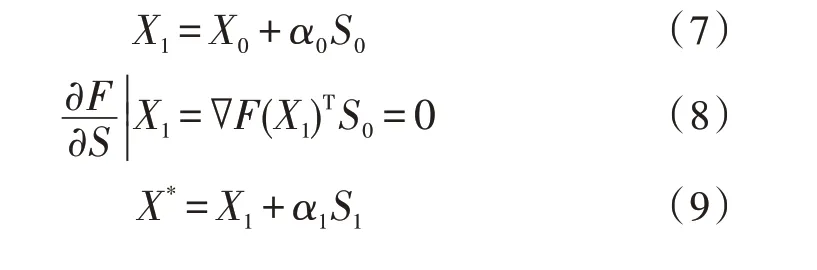
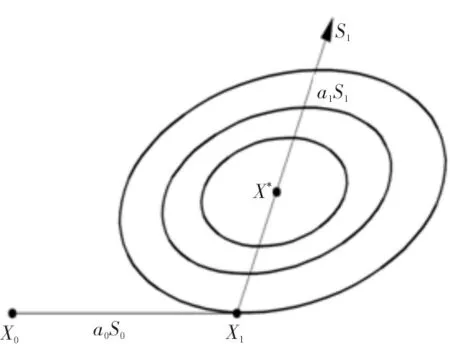
图1 二元二次函数搜索图

1.2 共轭方向法

共轭方向法具有二次终止性，是一个概念性算法，实现算法的关键在如何选取共轭方向[11]，不同的选取会产生不同的共轭方向法。其通用格式如下：

第一步：任取X0∈Rn,0 ≤ε＜＜1,k=0，计算g0=g(X0)和初始点X0的下降方向d0，s.t.；第二步：求解minf(Xk+αdk),λ≥0，得解αk(即αk是一维搜索的最优解)；

第三步：计算αk、Xk+1，使得Xk+1=Xk+αkdk；

第四步：若Xk+1满足迭代终止准则‖gk+1‖≤ε，停止迭代，输出Xk+1；否则，转至第五步；

第五步：根据共轭方向的构造方法获得搜索方向dk+1，使得dTk+1Gdj=0,j=0,1,…,k。令k=k+1，转至第二步。

共轭方向法的程序流程图如图2 所示。

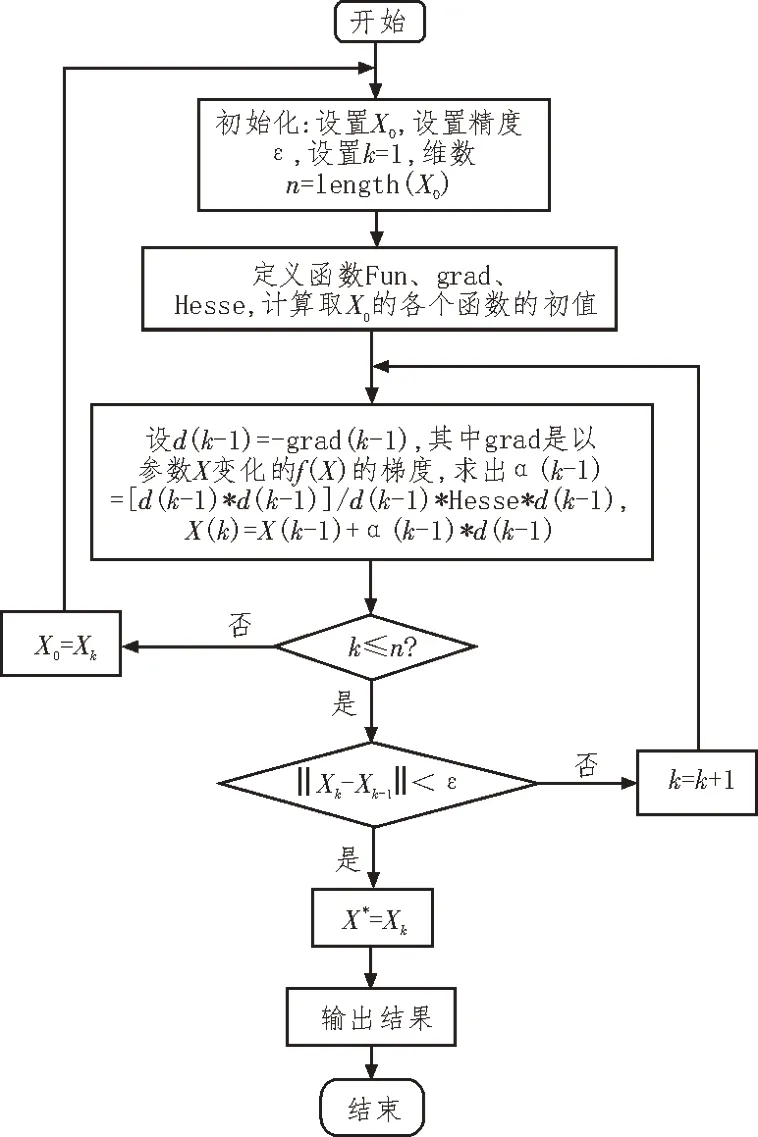
图2 共轭方向法的程序流程图

2 有限元分割共轭方向法

许多优化算法在理论上是用来解决无约束优化问题的，但是在实际工程问题中往往需要解决的是有约束的优化问题[12]，所以一些有约束优化问题往往采用无约束优化算法进行求解[13]。针对共轭方向法所求解有可能为局部最优解的问题，对共轭方向法加以改进，用以求解有约束的优化问题。算法执行过程如下所示：

第一步：任取X0∈Rn,X0=(x1,x2,…,xn)，若x1∈[a1,b1],x2∈[a2,b2],…,xn∈[an,bn],ai,bi∈R,i=1,2,…,n。将各个维数的取值区间进行有限分割，按各个维数的区间划分节点进行排列组合。例如：令xi=[ai,b1]∪[c1,c2]∪,…,∪[cm-1,cm]∪[cm,bi]，然后依次取区间分割节点ai,c1,c2,…,cm,bi为xi的值，最后将xi的节点其他xj的节点依次进行排列组合，取得初始点X0,m∈R,i≠j,i=1,2,…n,j=1,2,…n。

第二步：取初始点X0,0 ≤ε＜＜,1,k=0，计 算g0=g(X0)和初始点X0的下降方向d0,s.t.dT0g0＜0；

第三步：求解minf(Xk+αdk),λ≥0，得解αk(即αk是一维搜索的最优解)；

第四步：计算αk,Xk+1，使得Xk+1=Xk+αkdk；

第五步：若Xk+1满足迭代终止准则‖gk+1‖≤ε，停止迭代，输出Xk+1，将其保存于极值保存数组，然后转至第一步选取新的起始点；否则，转至第六步；

第六步：根据共轭方向的构造方法获得搜索方向dk+1，使得。令k=k+1，转至第三步。

第七步：根据极值保存数组所得各个极值中求取最小值点，最后输出在该约束内的全局最优解。

有限元分割共轭方向法的程序流程图如图3所示。

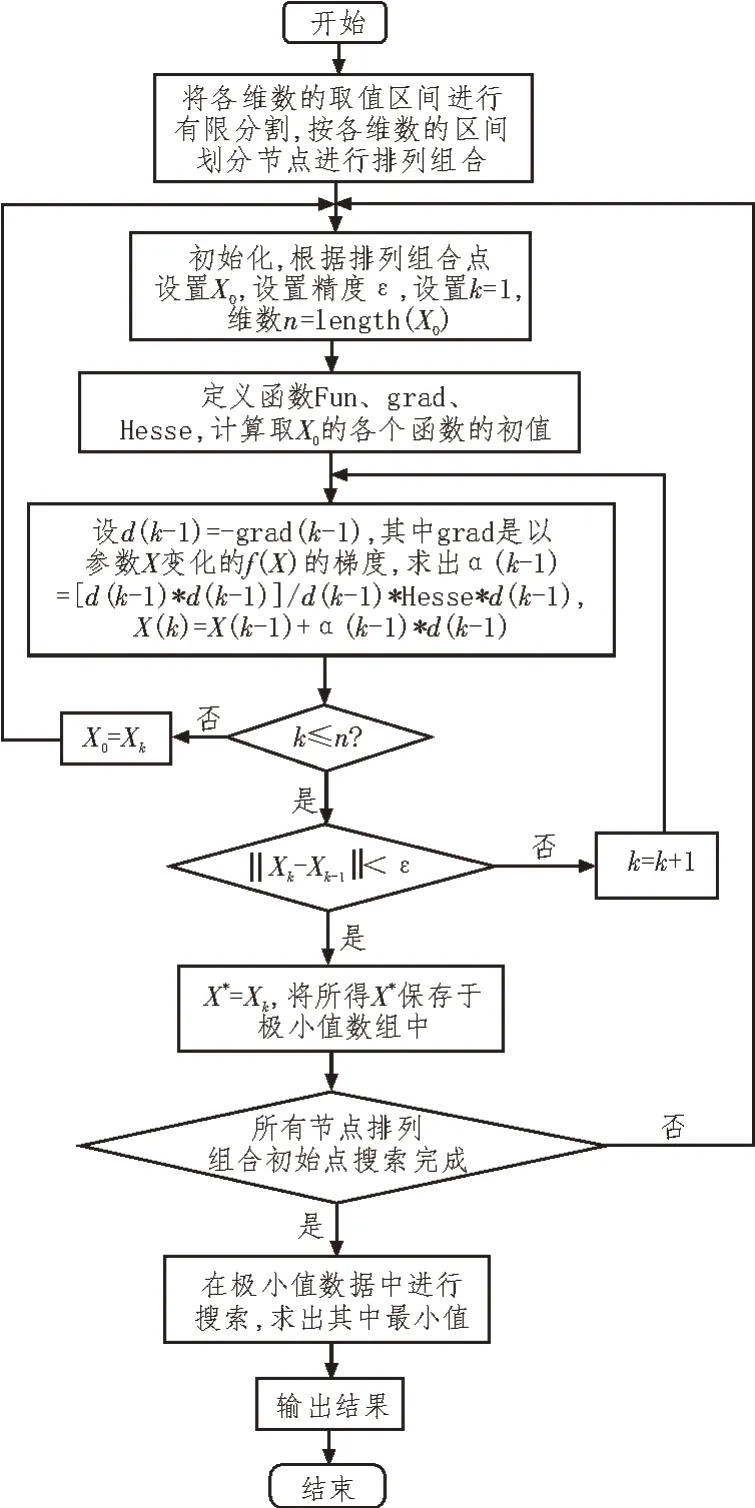
图3 有限元分割共轭方向法的程序流程图

3 目标函数的算例验证

以求解f(x)最小值为例：

目前多数优化问题的解决依赖于计算机软件，如MATLAB 软件的优化工具箱[14]，可用MATLAB 根据以上两种算法的执行过程进行编程，然后用所编程序分别求解以上目标函数的最优解。

3.1 共轭方向法的算例验证

根据图2 所介绍的共轭方向法的程序流程图用MATLAB 进行编程，定义精度为0.000 01，计算程序如下：

选取不同初值X0进行迭代计算，可以得到不同的极值和极值点，如表1 所示。

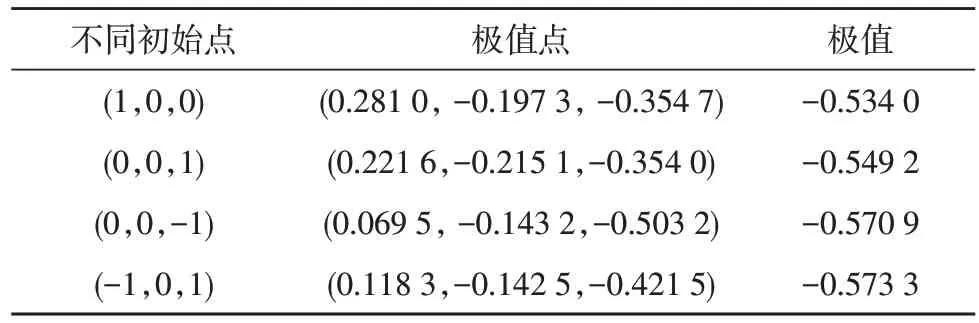
表1 共轭方向法不同初始点迭代结果

从计算结果可以看出，虽然定义的精度相同，但是选择不同的初始点进行迭代，所得到的极值点和极值各不相同，并且计算结果的差距较大。该结果充分证明了共轭方向法存在的缺点，会陷入局部极值而无法找到全局最优点。就科技的发展而言，计算速度已不是问题，最主要的问题是计算结果的准确度，这就意味着需要更优的计算方法解决准确度问题[15]。

3.2 有限元分割共轭方向法的算例验证

根据图3 的有限元分割共轭方向法的程序流程图进行MATLAB 编程，定义精度也为0.000 01，并设置预期极值为0(所设预期极值应大于最终计算极值，如果所设预期极值不大于计算极值，计算结果将会是设置的预期结果，需重新设置预期极值进行重新计算)，计算程序如下：

令初始点X0=(x1,x2,x3)，由题知x1,x2,x3∈[-1,1]，设每个分割单元的长度均相等，分割单元长度为0.1，则x1、x2、x3的分割节点可取为-1,-0.9,…,0.9,1。将所设参数代入所编程序中进行迭代计算，可以得到最终的极值和极值点，如表2 所示。

表2 有限元分割共轭方向法迭代结果

由表2 所得极值与表1 所得极值进行对比，可以得出表2 所得极值小于表1 所有极值。这说明有限元分割共轭方向法的迭代结果优于共轭方向法，并且可以避免在求解过程中陷入局部最优解的缺点。通过编程验证可知，当有限元分割共轭方向法的分割单元长度越小，则所得解越优，就当今科技发展的程度，计算速度已不是问题[16]，所以该优化计算算法具有很大的实际应用价值。

4 结论

该文在共轭方向法的基础上提出了有限分割的共轭方向法，并通过MATLAB 编程对两种算法的寻优结果进行对比，可得出的主要结论如下：

1）提出的有限元分割共轭方向法的迭代结果优于共轭方向法，并且可以避免在求解过程中陷入局部最优解的缺点。

2）有限元分割共轭方向法具有可移植性，可以根据不同的问题可以进行不同参数设置，可以作为求解大规模优化问题的主要方法。

3）有限元分割共轭方向法克服了最速下降法的慢收敛性，并且保留了共轭方向法的优点，具有二次终止性。

4）有限元分割共轭方向法具有简单、易于编程、需要的储存空间小等优点。

5）有限元分割共轭方向法不受维度限制，可以用于多维问题的求解。

6）当有限元分割共轭方向法的分割单元长度越小，则所求解越优。