时滞下忆阻突触耦合Hopfield神经网络的动力学行为分析*
马杰 高洁 独盟盟 杨丽新
(陕西科技大学文理学院,西安 710021)
引言
在人工神经网络领域中,Hopfield神经网络一直是一类重要的神经网络模型,并且广泛应用于联想记忆、模式识别、数据储存、保密通信等各个领域[1].换个方面,从动力学角度来看的话,Hopfield神经网络模型是一个复杂的非线性系统,有着丰富的动力学行为,而这些丰富的动力学特性对网络有着重要的影响[2].文献[3]介绍了神经动力学在各个领域的发展及应用,以及利用神经动力学来揭示神经系统中的一些独特现象和规律.
忆阻有着类似大脑神经突触在生物电信号激励下的非线性电学特性,因此,忆阻可被用于模拟突触,并用之来构建忆阻型神经网络.利用忆阻可实现神经网络模型连接权重的可变性,能够有效地模拟神经网络的动力学行为[4-6].根据法拉第电磁感应定律,细胞内外的带电离子穿越细胞膜会产生电磁感应效应.因此在传统的神经模型引入磁通变量并研究磁感应对电活动模式的影响更具有实际意义.利用磁控忆阻器来实现神经元磁通量与膜电位之间的耦合,进一步来模拟神经元间膜电位差引起的电磁感应电流[7].电磁感应在调节神经网络的动态行为中起重要作用,而将忆阻突触引入生物神经网络为揭示人脑神经系统的记忆行为提供有用的线索[8].
自突触是神经元连接自身的特殊结构,这种自突触通常称为电性自突触,其对神经元膜电位的调制可以表示为Iout=r(x(t-τ)-x(t)),r表示反馈增益,τ表示信号传递过程中引发的时滞.电自突触能够影响神经元的放电行为,甚至诱发一类周期性、混沌放电等现象,此外还可以调控神经元网络群体的电活动规律以及神经元之间的迁移[9].而神经元之间的信息表达和信息传递是通过动作电位实现的,因此在实现过程中难免会出现延迟的行为,时滞不仅会影响神经元系统的稳定性,而且也会在某些条件下诱发出复杂的动力学行为,故在神经网络中引入时滞具有重要的意义[10].文献[11]研究了含时滞的忆阻耦合HR神经元系统,讨论了平衡点的局部稳定性以及时滞对神经元系统动力学行为产生的影响.在神经形态中,多稳定性对神经元的记忆以及信息处理都有着显著的影响,因此从动力学角度来阐述系统平衡点的稳定性,有助于深入解释神经动力学方面对脑功能的影响.
本文在文献[12]的基础上加入时滞,构建了一种由时滞诱发的四维忆阻HNN模型,在两个神经元之间引入了非理想忆阻突触,探究零平衡点处系统的动力学,并且随着时滞增加到一定程度时,系统只会诱导出周期解;分析系统随忆阻耦合强度k产生的动力学行为变化,并且加入固定的时滞改变忆阻耦合强度来与无时滞时不同忆阻耦合强度下系统的动力学行为进行比较,观察系统的动力学行为变化规律;发现在不同的忆阻耦合强度下,系统存在着周期极限环、混沌吸引子等动力学行为.
1 数学模型与稳定性分析
1.1 数学模型
磁控忆阻突触的数学模型[12]:

其中,φ为忆阻内部状态变量,W(φ)=kφ为忆导函数表达式,k为非理想忆阻耦合强度,UEM为神经元之间的膜电位差,IEM为神经元1和神经元2之间膜电位差作用于非理想忆阻突触所产生的磁感应电流.为了简化分析,神经元1和神经元2保留完整的突触连接,非理想忆阻突触耦合位于神经元1和神经元2之间,电自突触位于神经元3上,基于文献[12]的3神经元HNN,将时滞加于神经元3上,神经元3仅与其他神经元单向连接,则构建的时滞下忆阻突触耦合的4维HNN的表达式为:

其中,xi为第i个神经元的状态,k为非理想忆阻突触的耦合强度,双曲正切函数tanh(xi)表示从第i个神经元电压输入的神经元激活函数,系数aij表示突触权重,也就是表示两个相邻神经元之间的连接强度,r表示电自突触.
原点(0,0,0,0)为系统的零平衡点,则在零平衡点附近的线性化系统的特征方程为:
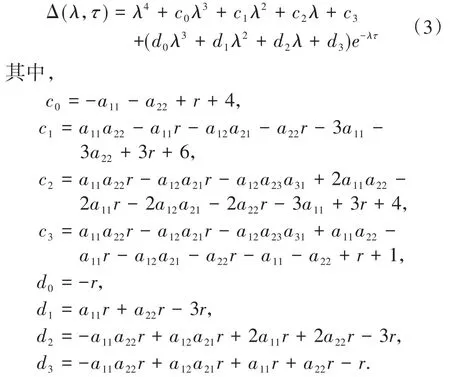
1.2 稳定性与Hopf分岔
为确定系统的稳定性,首先考虑τ=0的情况,当τ=0时,
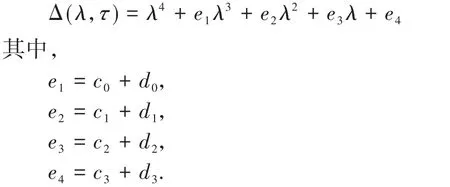
根据Routh-Hurwitz判据可知,当Δi>0时系统稳定,其中,
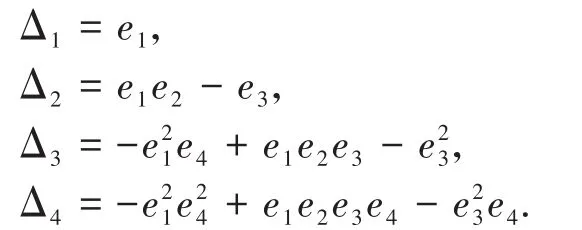
当τ>0时,若方程(3)有一对纯虚特征根为λ=iw,则
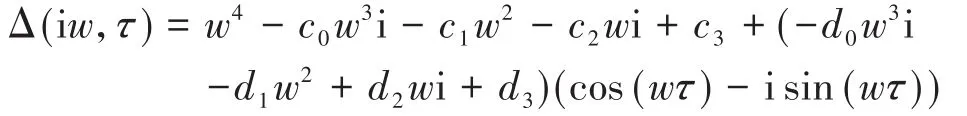
分离实部与虚部,

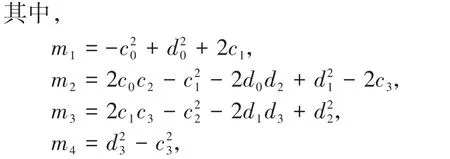
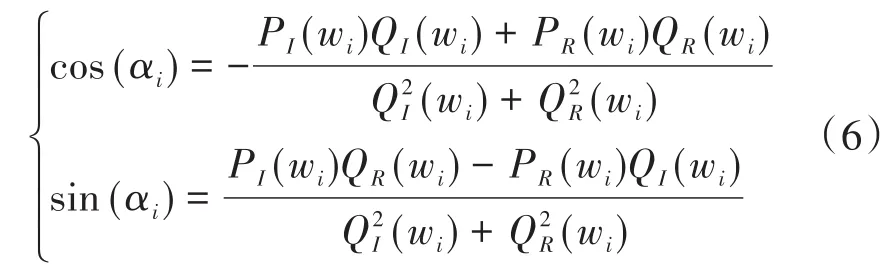
则根据微分方程稳定性与分岔理论[3]可知:当Δi>0时有:
1.若式(5)无正实根,则系统的零平衡点是全时滞局部渐进稳定.
2.若式(5)存在正实根,则存在某个常数τ0> 0,使得系统的零平衡点在τ∈ (0,τ0)内是局部渐进稳定的,并且系统在τ=τ0发生Hopf分岔,产生周期运动,其中τ0=min(τi,j).
2 数值算例
取系统参数为a11=-0.1,a12=0.6,a31=0.1,a21=0.15,a22=0.2,a23=0.05,r=-2,k=-0.5.此时经过计算可得Δ1=3.9>0,Δ2=18.436>0,Δ3=53.438>0,Δ4=45.367>0.根据Routh-Hurwitz判据可知,系统的特征根均有负实部,那么零平衡点是局部渐进稳定的.当τ>0时,式(5)可写为:
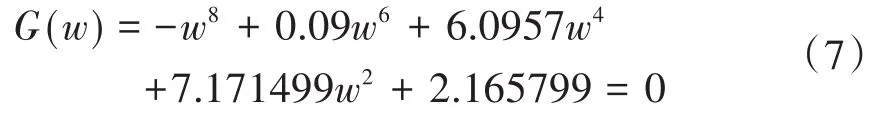
解得唯一正实根w=1.73191813,则由式(4)可得相应的一组临界时滞τj=0.605,4.232,...根据定理可知:当τ∈[0,0.605]时,系统的零平衡点是渐进稳定的,而当τ>0.605时,系统的零平衡点是不稳定的.因此,当τ=0.605时,系统发生了Hopf分岔.
给定初始条件为(1.2,0.5,-1.2,0.3),当时滞τ=0时,系统的响应图(系统的时间序列曲线)如图2所示.由图2可知,当时滞τ=0时,此时系统在零平衡点处是渐近稳定的.当τ=0.55和τ=0.606时,系统的响应图如图3所示.由图3(a)可知,在τ=0.55时系统状态收敛到零平衡点;在τ=0.606时,由图3(b)可知系统在零平衡点失去稳定性,出现了振荡,这与定理的结论相一致.
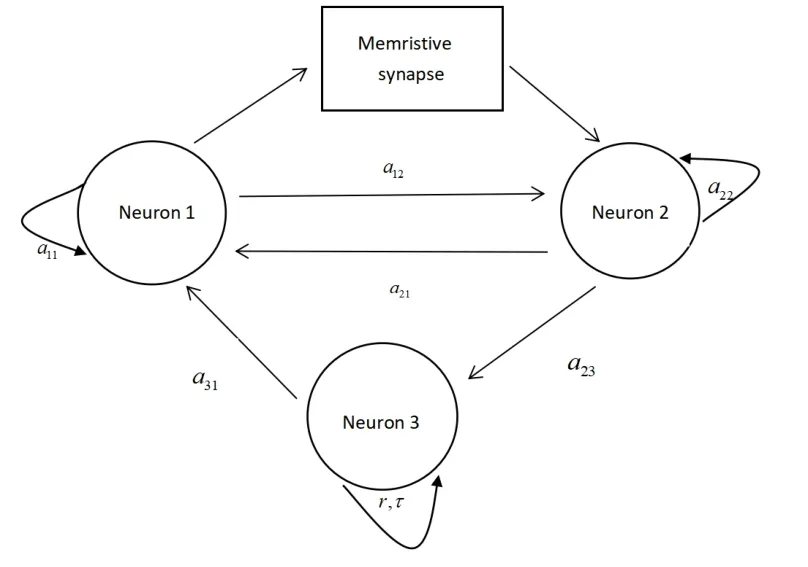
图1 基于非理想忆阻型突触的HNN的连接拓扑Fig.1 Connection topology of HNN based on non-ideal memristive synapse
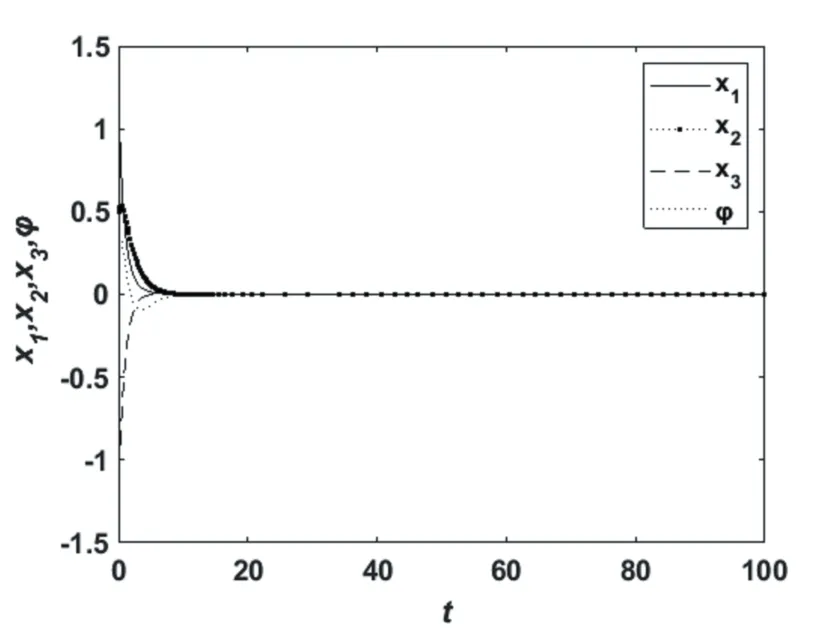
图2 τ=0时的系统响应图Fig.2 System response graph whenτ=0
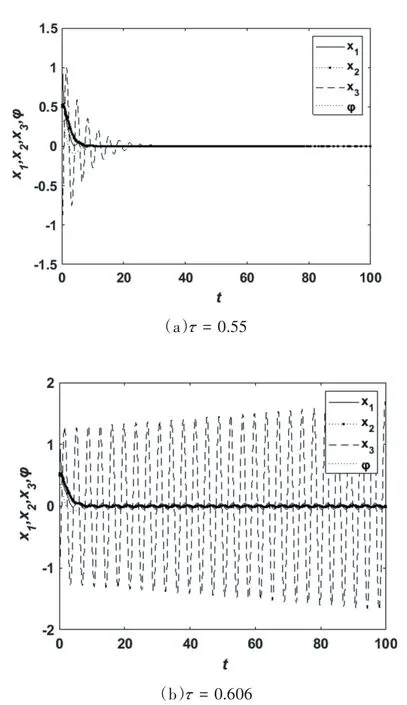
图3 τ=0.55及τ=0.606时的系统响应图Fig.3 The system response diagram whenτ=0.55andτ=0.606
3 时滞和忆阻耦合强度对系统动力学的影响
3.1 时滞对系统在平衡点稳定性的影响
当取系统参数为a11=-1,a12=4,a31=-5,a21=0.5,a22=-2,a23=3,r=0.5,k=-0.3时,系统给定初始值为(1.2,0.5,-1.2,0.3),做出不同时滞下系统的时间序列曲线以及x2-x3平面的相图.
由图4可知,当时滞τ=0.2时,系统在平衡点(0,0,0,0)是不稳定的,此时系统发生周期振荡.如图5所示,当时滞为τ=0.8时,系统在平衡点(0,0,0,0)是局部渐进稳定的,此时系统响应图也表明系统在平衡点处是局部渐进稳定的.
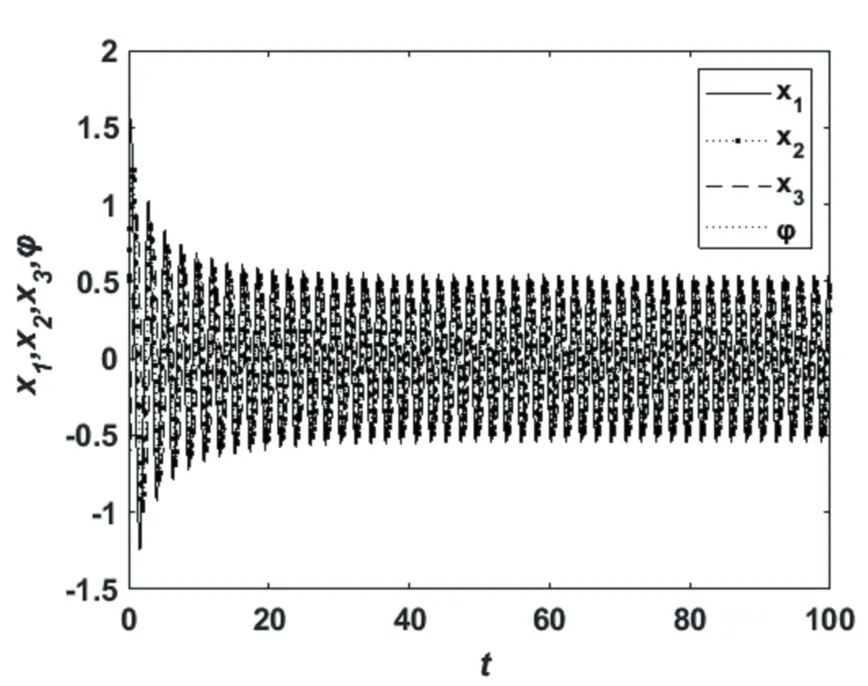
图4 τ=0.2时的系统响应图Fig.4 The system response diagram whenτ=0.2
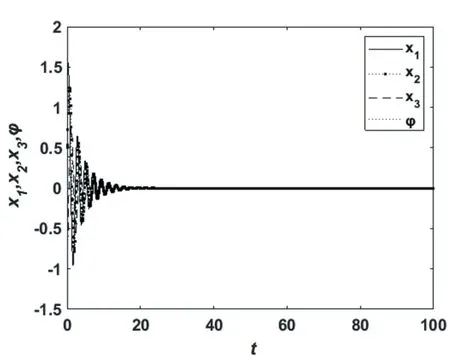
图5 τ=0.8时的系统响应图Fig.5 The system response diagram whenτ=0.8
当时滞增加到τ=3.4时,图6的系统响应图与相图表明此时系统在平衡点处是局部渐进稳定的.由图7可知,当时滞τ=10时,系统在平衡点(0,0,0,0)是不稳定的,此时系统发生周期振荡.由图8可知,当时滞τ=13时,系统在平衡点(0,0,0,0)是不稳定的,此时系统为概周期运动.
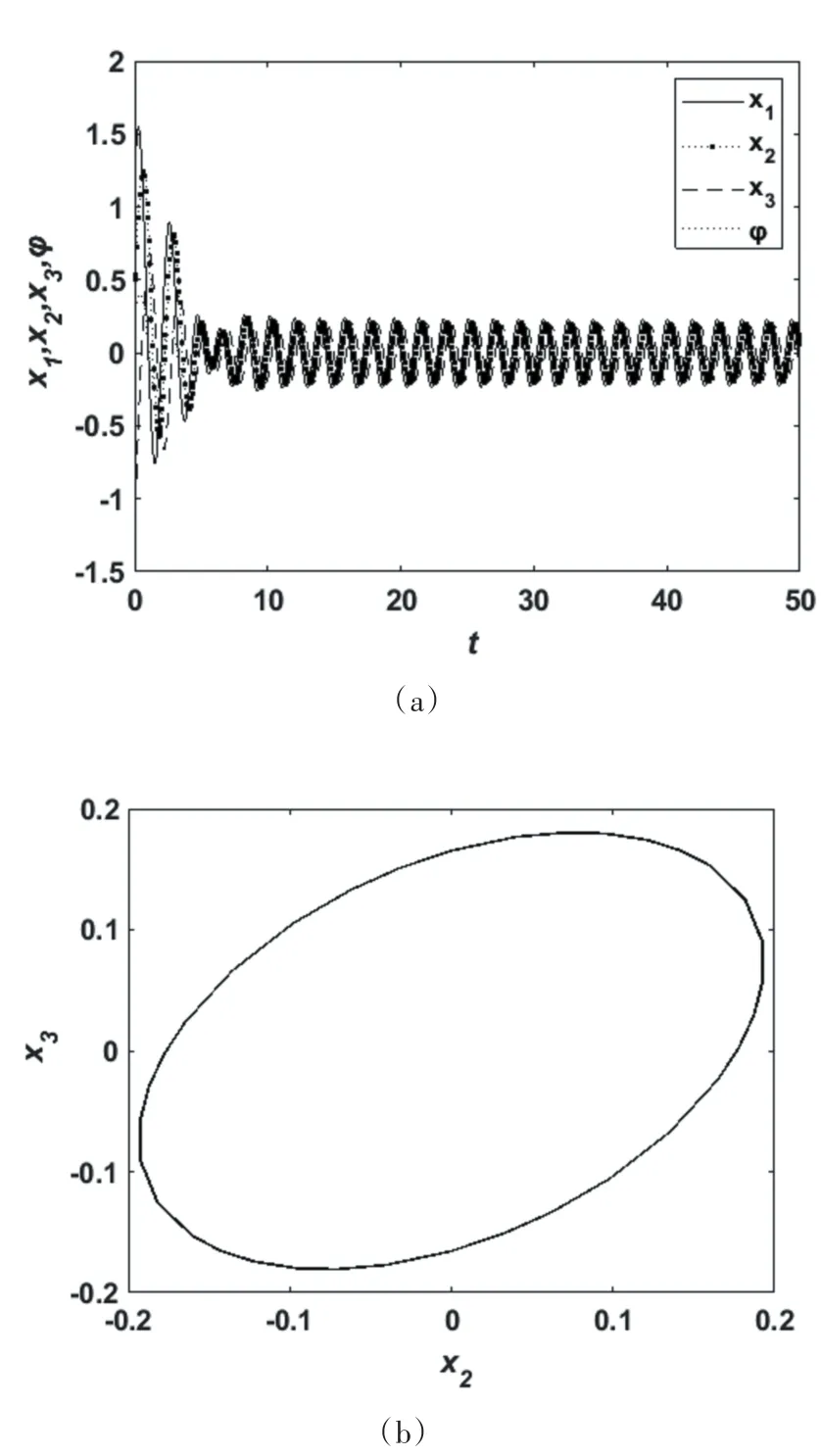
图6 τ=3.4时的系统响应图及在x2-x3平面的相图Fig.6 The system response diagram whenτ=3.4and the phase diagram on thex2-x3plane
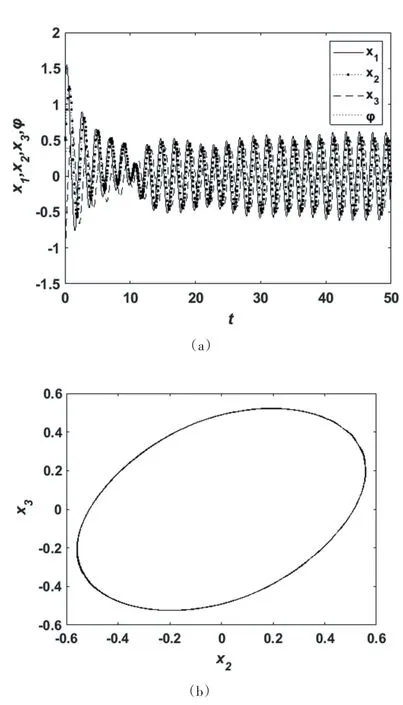
图7 τ=10时的系统响应图及在x2-x3平面的相图Fig.7 The system response diagram whenτ=10and the phase diagram on thex2-x3plane
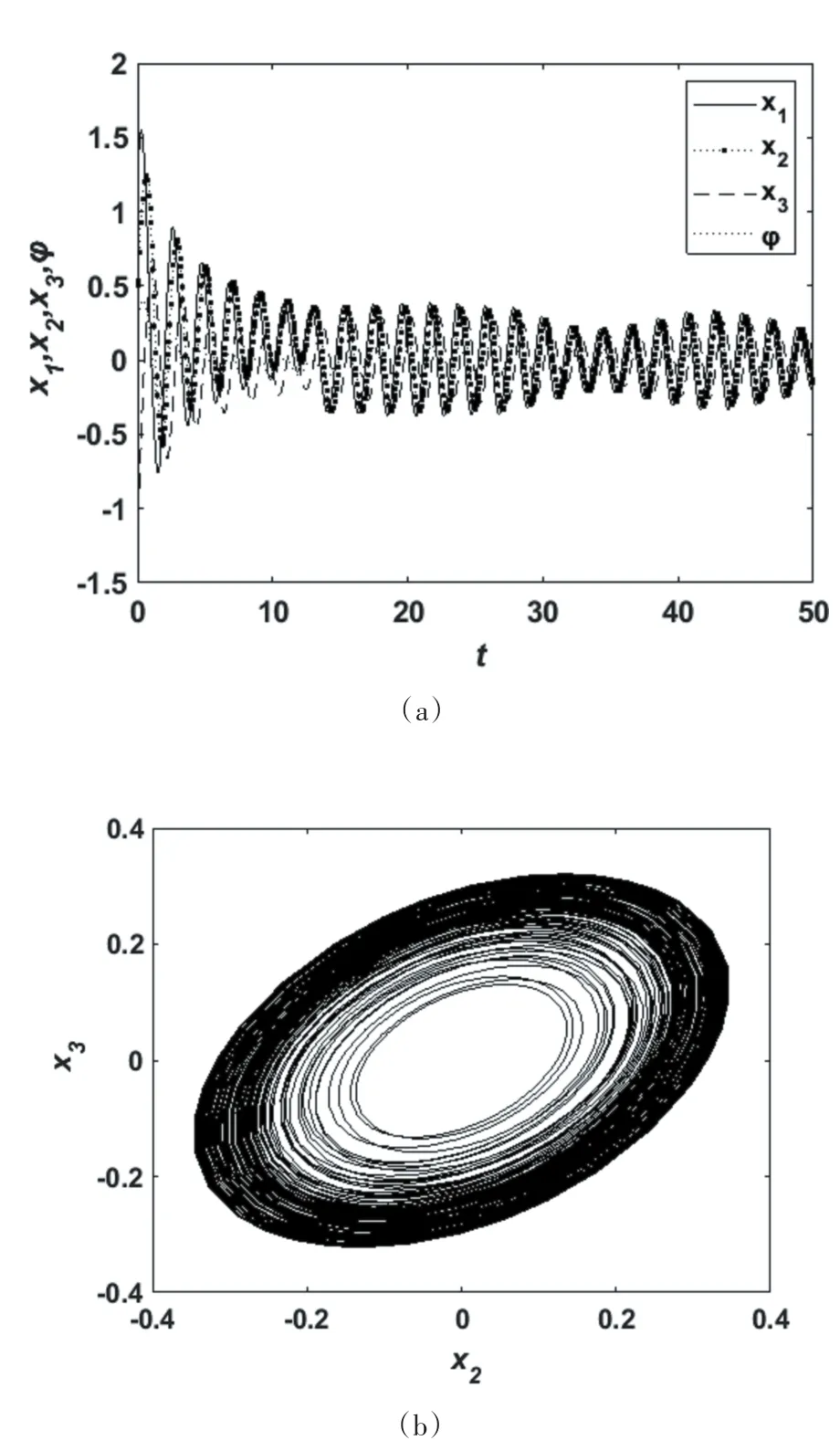
图8 τ=13时的系统响应图及在x2-x3平面的相图Fig.8 The system response diagram whenτ=13and the phase diagram on thex2-x3plane
故由上可知,系统存在一组临界时滞,当改变时滞时系统在零平衡点处的状态也会有所不同,因此,随着时滞的改变,系统的动力学行为也随之改变.随着时滞从零增大,系统在稳定平衡点、周期运动之间发生有限次切换,相应存在的一系列临界时滞可由式(6)计算可得,并且在时滞增加到某个值之后,系统一直为周期运动.
3.2 时滞下系统随忆阻耦合强度变化的动力学
文献[12]给出了无时滞时系统在不同忆阻耦合强度下会产生多个不稳定平衡点,说明系统可以产生混沌吸引子,且易产生依赖于状态初值的多稳定现象.若在系统中某个神经元加入固定的时滞,通过改变忆阻耦合强度k来观察系统的动力学行为变化.给定系统参数为a11=1.5,a21=2.8,a22=1.2,a23=-20,a31=0.5,a12=-1.5,r=0.5.由于系统对初值非常敏感,给定系统不同的初值(0,10-4,0,0)与(0,-10-4,0,0),取不同的忆阻耦合强度k,观察两组初值在x1-x3平面相图的变化.
系统无时滞时,图9(a)为忆阻耦合强度k=0时,系统在平面的相图,此时系统存在共存的周期极限环;当忆阻耦合强度k=0.7时,如图9(b)所示,此时系统存在共存的周期极限环和混沌吸引子;当忆阻耦合强度k=-0.4时,如图9(c)所示,此时系统存在混沌吸引子.
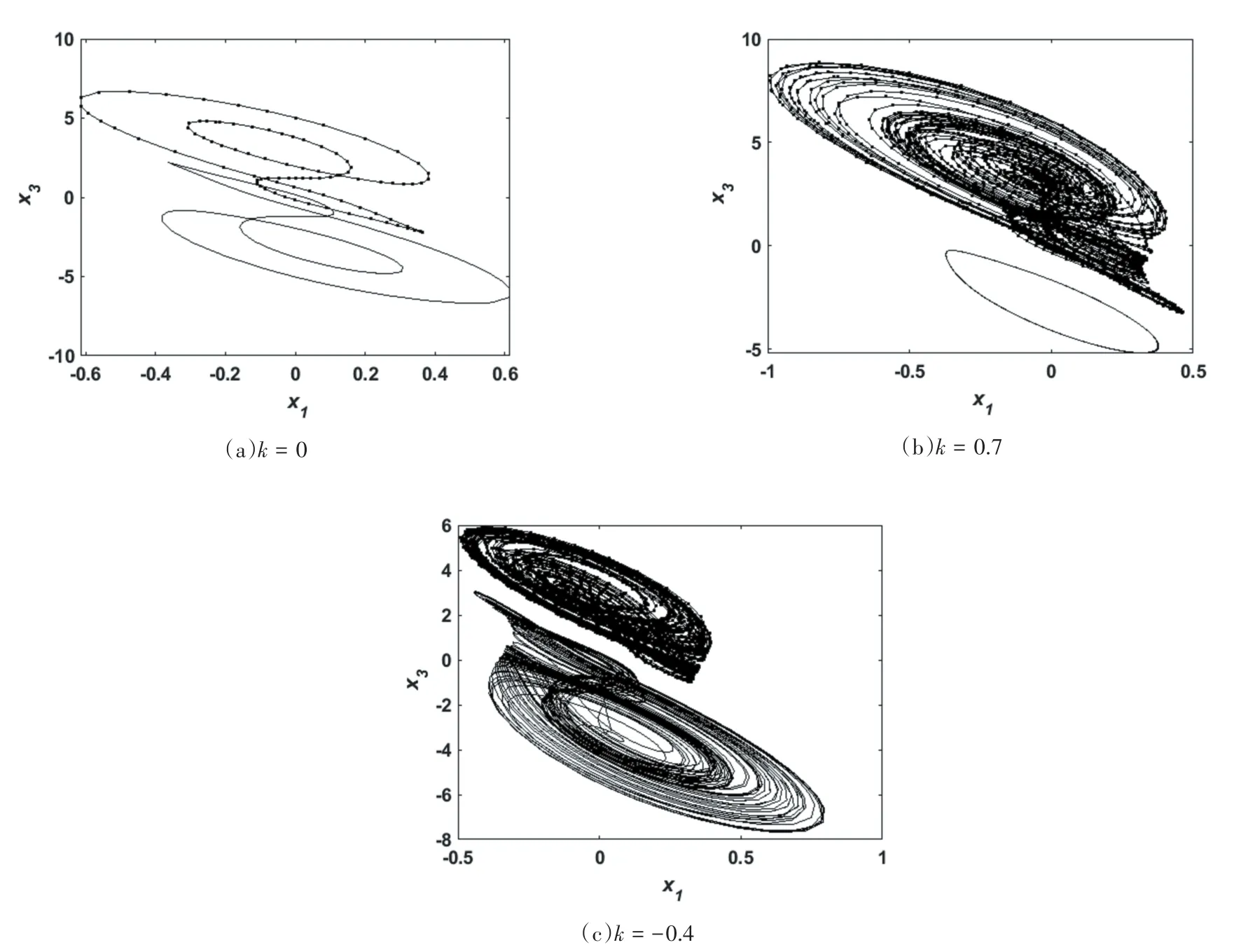
图9 τ=0时不同忆阻耦合强度下系统在x1-x3平面的相图Fig.9 Phase diagram of the system in thex1-x3plane withτ=0and different memristive coupling strengths
当在系统中加入固定时滞τ=0.5,图10(a)为忆阻耦合强度k=0时,系统在x1-x3平面的相图,此时系统存在多周期极限环;当忆阻耦合强度k=0.7时,如图10(b)所示,此时系统存在周期极限环;当忆阻耦合强度k=-0.4时,如图10(c)所示,此时系统存在多周期极限环.
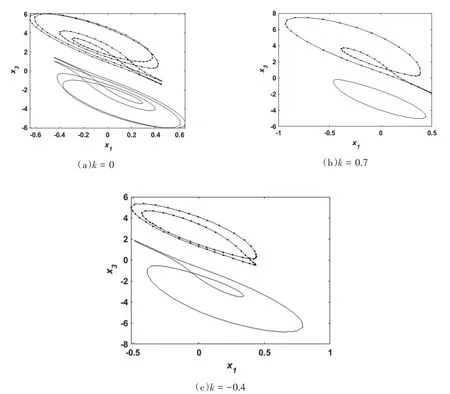
图10 τ=0.5时不同忆阻耦合强度下系统在x1-x3平面的相图Fig.10 Phase diagram of the system in thex1-x3plane withτ=0.5and different memristive coupling strengths
在系统中加入固定时滞τ=2,图11(a)为忆阻耦合强度k=0时,系统在x1-x3平面的相图,此时系统存在周期极限环;当忆阻耦合强度k=0.7时,如图11(b)所示,此时系统存在周期极限环;当忆阻耦合强度k=-0.4时,如图11(c)所示,此时系统存在周期极限环.
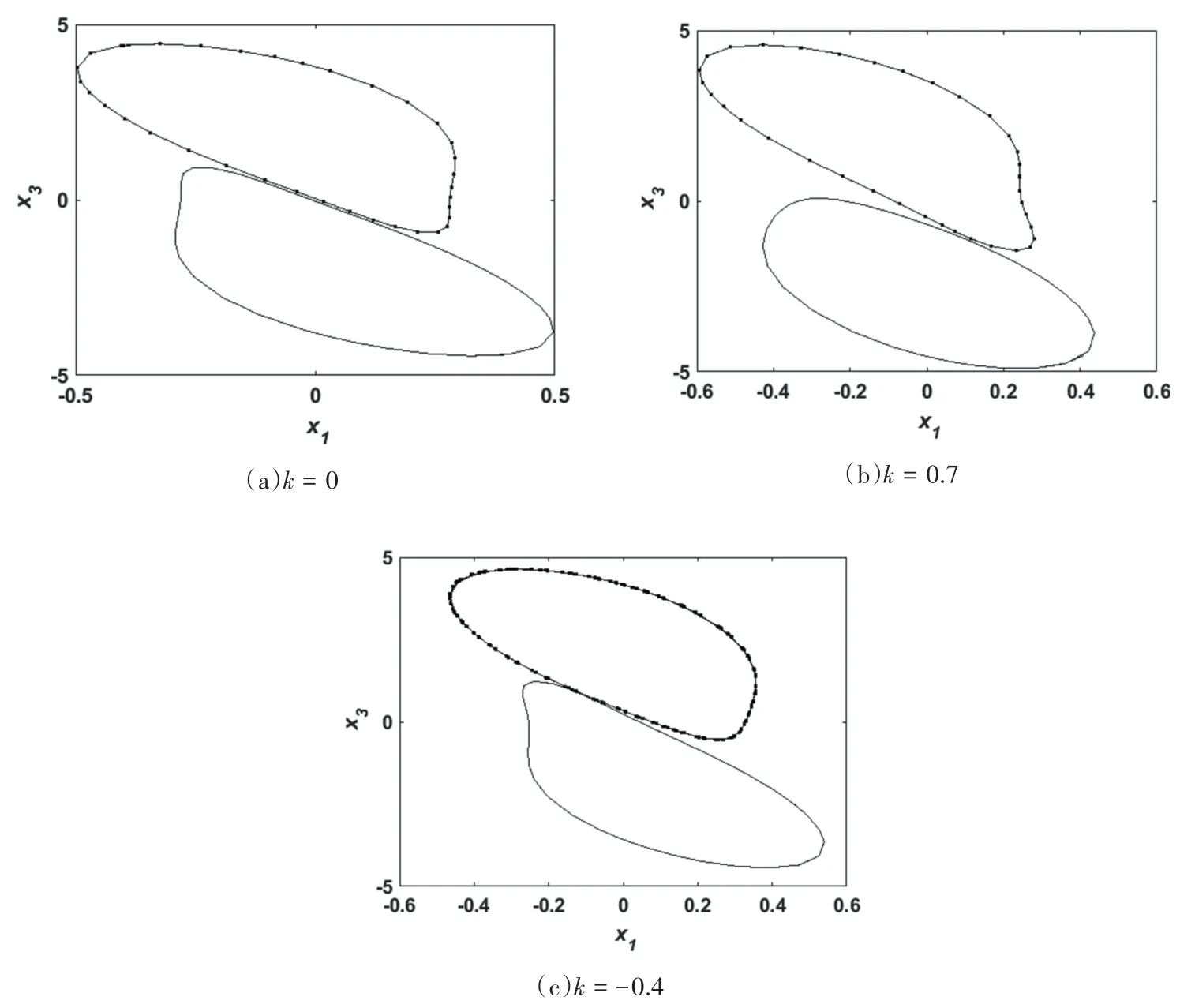
图11 τ=2时不同忆阻耦合强度下系统在x1-x3平面的相图Fig.11 Phase diagram of the system in thex1-x3plane withτ=2and different memristive coupling strengths
但是当时滞增加到τ=5时,此时系统在不同的忆阻耦合强度下的动力学又发生了变化,并且系统由τ=2时存在的周期极限环变为更为复杂的多周期极限环、共存的周期极限环和混沌吸引子.
因此在系统无时滞时,系统的动力学行为是十分丰富的,例如存在混沌吸引子,共存的周期极限环和混沌吸引子等.但是给系统加入固定时滞后,在不同的忆阻耦合强度下系统的动力学行为也发生了改变.
4 总结
本文研究了含有时滞的忆阻突触耦合型Hopfield神经网络,根据特征方程的根分布情况得到了系统在零平衡点处的稳定性以及系统失稳时发生Hopf分岔的时滞条件.探究了时滞以及忆阻耦合强度对系统动力学行为的影响,并通过数值模拟揭示了多种有趣的动力学现象,如混沌吸引子、周期极限环等.
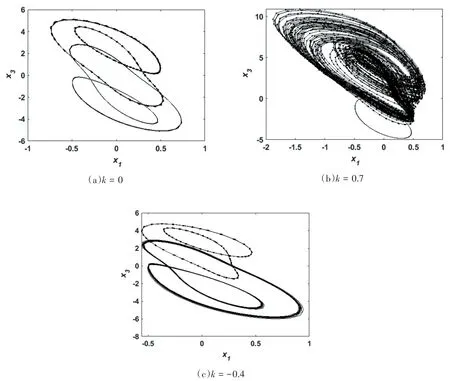
图12 τ=5时不同忆阻耦合强度下系统在x1-x3平面的相图Fig.12 Phase diagram of the system in thex1-x3plane with andτ=5different memristive coupling strengths

