多波束渔用声呐波束成形算法设计与FPGA实现

程 婧，王志俊，李国栋，魏 珂

(中国水产科学研究院渔业机械仪器研究所，上海 200092)

渔用声呐作为在渔业领域利用声波对水下鱼群进行探测的重要助鱼仪器[1]，近几十年来，在海洋捕捞渔业中发挥重要作用[2]。渔用声呐从利用声波波束的角度可分为单波束[3]、分裂波束[4]、多波束等多种方式[5]，其中多波束渔用声呐通过多个换能器阵子协同工作，可在较短的时间内进行扫海，相较于单波束可以更加准确地探测较大范围内的鱼群距离和方位[6-7]，主要在中大型围网和拖网捕捞渔船上使用[8]，提高了捕捞效率[9-11]。

波束成形作为多波束声呐的一项核心技术，是一种抗噪声和混响干扰的主要方法[12]，其实现性能决定了声呐探测距离和空间分辨能力[13]。相位补偿的波束成形方法资源占用少且运算速度较快，在窄带波束成形中有较多使用。相较于窄带技术，宽带技术由于具有更好的抗混响和距离分辨能力[14]被广泛应用在渔业探测中[15-17]，然而因其相位的实时变化，相位补偿的方法将不再适用。常用的宽带波束成形方法有时移法、频域变换法[18]和移边带波束成形法(SSB)等，其中时移法主要使用延时滤波器组对宽带信号中不同频率的信号幅度与相位加权[19]，其精度受采样周期的制约；频域变换法是先将宽带信号变换到频域，然后将多个频率分量，对不同频点的信号采用窄带波束成形进行波束合成，最后再变换到时域上[20]，其波束成形精度受频点精细度的影响，精细度越高运算量越大[12]；SSB算法采用下变频的方法，将较高的载频信号先搬移到较低频率然后进行相位和时间补偿，避免了采样率的限制，可在较低的采样率下达到较高精度，然而由于其相位和时间补偿过程采用并行运算，参与波束成形的阵子数越多，运算量和硬件资源占用量越大[21]，制约了其在渔船这类对空间和能耗要求较严苛的搭载仪器上的使用。

本研究根据现有硬件的资源和运算能力[22-23]，提出一种基于分布式的全方位渔用声呐多波束扫海方式，并对SSB算法进行改进，采用串行处理代替原有算法的大量并行运算，并结合FPGA的特性[24-25]采用时分复用设计，实现了在未降低算法性能的同时，大量节省片上资源，并提高了信号处理速度。

1 圆柱阵多波束渔用声呐全向扫海方式

多波束探鱼仪工作时，采用旋转定向扫描发射，即在某一时刻一个扇区内同时发射多个波束，然后在下一时刻水平旋转至下一扇区继续发射多个波束，以便保证各个方位都可以被波束覆盖到。对于多波束探鱼仪的接收部分采用多个阵子同步接收，并对回波进行信号处理。

接收波束成形中的关键环节是对各个阵子接收相位延时进行精准的控制与计算[26-27]，使得回波波束的聚焦点小，指向性好从而获得更加清晰的图像。

由于圆柱阵换能器的阵子较多，单板无法对信号进行处理，因此为了提高波束成形的运算速度，采用分布式跨板间计算。所用换能器基阵采用8块多通道接收机构成，每块多通道接收机由32个阵子组成，共计256个阵子组成所需圆柱阵。

如图1、2所示为每块多通道接收机中的阵子排列方式：水平方向上共4列换能器，每列由8个阵子组成，相邻两列阵子与坐标系中心连线的夹角为11.25°，每个多通道接收机可以分别与其左侧和右侧的多通道接收机组成对应虚拟扇区。该探鱼仪在垂直方向上两个阵子之间的间距为0.042 m，单个阵子的半径为0.185 m，指向性开角约为78°，圆柱阵周长为1.18 m。每个扇区可以完成20个波束，从-21.375°至21.375°，波束间隔为2.25°。单个多通道接收机参与40个波束，前20个波束与其右侧的多通道接收机一起完成，后20个波束与其左侧多通道接收机一起完成。

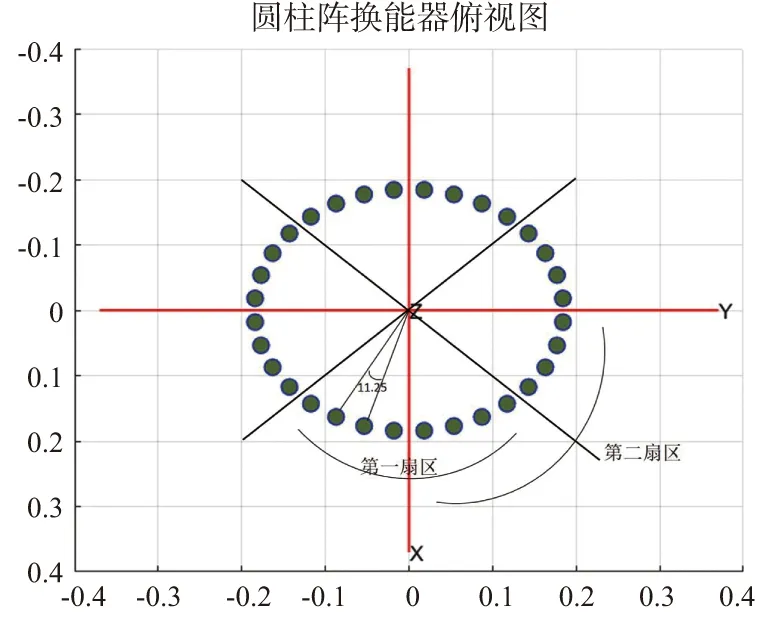
图1 扇区划分Fig.1 Sector division

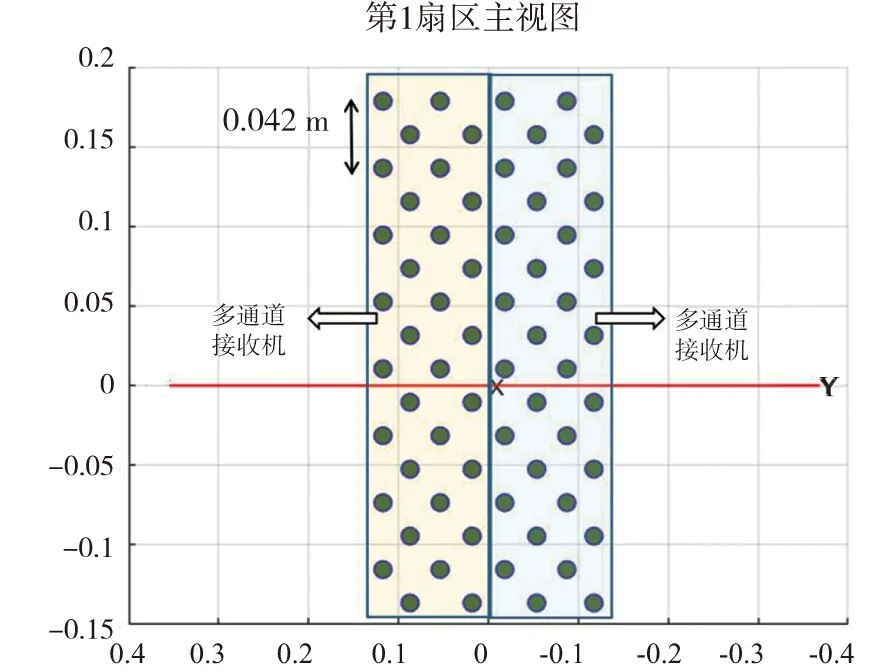
图2 第一扇区Fig.2 First sector

2 波束成形算法改进

2.1 传统移边带波束成形算法

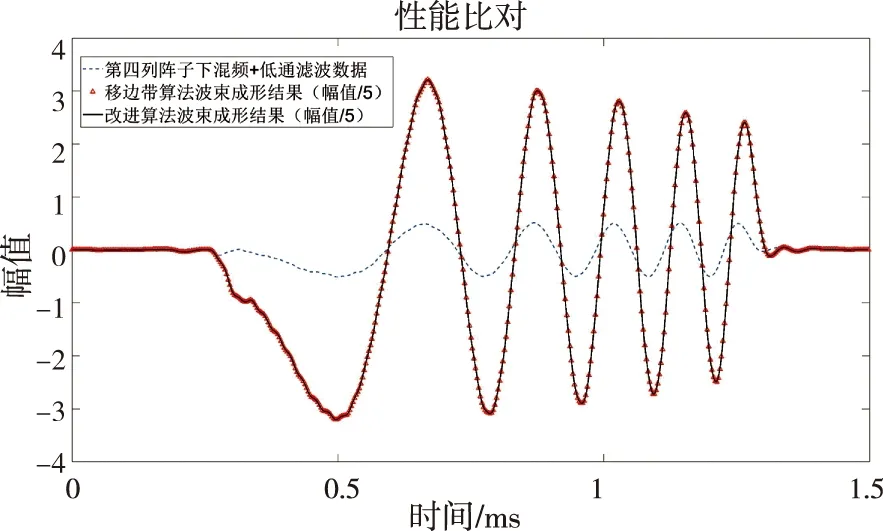
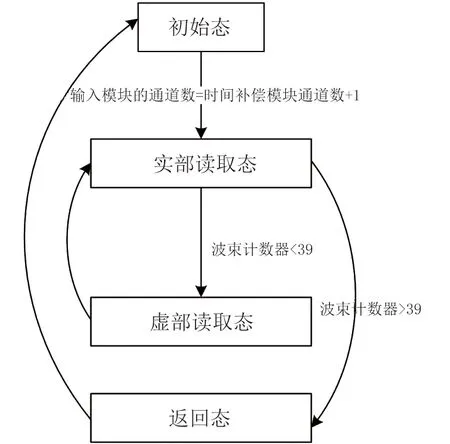
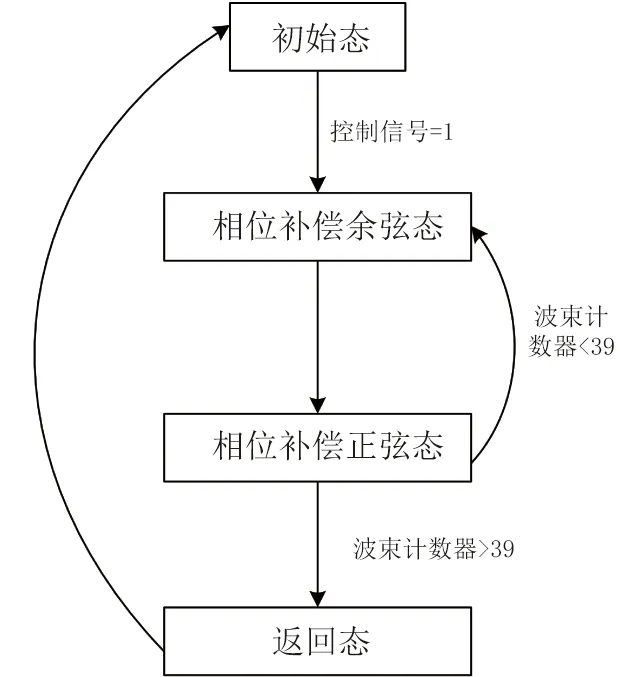
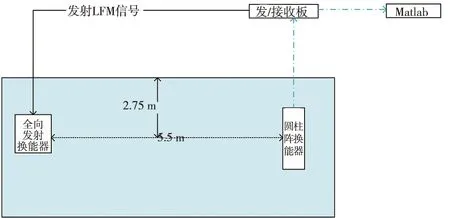
移边带波束形成算法原理如图3所示，具体为将接收到的信号移动f1至中频f0-f1，信号被调制为exp(-iω1t)的限制条件为：0

波束成形的输入信号形式见(1):

xm(t)=x(t-τm)exp[iω0(t-τm)]

(1)

式中：xm为阵子m接收到的回波信号(m=1,2,3,...,M)；τm为阵子m相对于坐标原点的时延值，s；ω0为基带信号的中心角频率，rad/s。经过下混频模块，可得到信号的实部与虚部分别为：

xsmr(t)=xm(t)×2cos(ω1t)

(2)

xsmi(t)=xm(t)×2sin(ω1t)

(3)

式中：xsmr与xsmi分别为经过下混频模块后的实部与虚部信号；ω1为载波信号的角频率，rad/s。当下混频后的信号经过低通滤波器，可将(ω0+ω1)过滤掉，仅保留(ω0-ω1)，此时对应的信号表达式为：

xfmr(t)=x(t-τm)[cos(ω0-ω1)t-ω0τm)+jsin(ω0-ω1)t-ω0τm)]

(4)

xfmi(t)=x(t-τm)[sin(ω0-ω1)t-ω0τm)-jcos(ω0-ω1)t-ω0τm)]

(5)

式中：xfmr与xfmi分别对应经过低通滤波的实部与虚部信号。将低通滤波后的信号经过相位补偿后输出信号见公式(6)。

xmpn(t)=xfmr(t)×cos(ω0τm)-xfmi(t)×sin(ω0τm)=x(t-τm)exp[i(ω0-ω1)t]

(6)

式中：xmPn为阵子m的波束n相移之后的信号(m=1,2,3，...，M，n=1,2,3，...，N)。

(7)

式中：bn为累加过后的第n个波束(n=1,2,3，...，N)；m为对应的阵子数(m=1,2,3，...，M)。

2.2 算法改进

全方位圆柱阵多波束渔用声呐算法是在SSB算法的基础上进行改进，主要调整了模块的顺序，采用时分复用的技术，将传统的并行结构进行了串行处理，且采用分布式多板同步的方式进行波束累加(图4)。

图4 算法改进原理框图Fig.4 Diagram of the improved algorithm

移时模块的串行处理如图5所示，每个阵子对应的存储器分别存储N个波束的补偿参数，将低通滤波的输出依次写入对应的缓冲区，同时额外存在一个指针，根据传入的补偿参数在此指针位置上进行对应地址的读取，最后依次串行输出N个波束的实部和虚部至对应阵子的相位补偿模块进行下一级的运算。与图3相比，模块数量由原来的M×N个变为现在的与阵子数M保持一致，减少了FPGA存储器的资源同时提高了后续在FPGA中信号处理的运算速度。

图5 改进算法的串行处理原理Fig.5 Principal of the improved algorithm with serial processing

2.3 两种算法仿真比较

基于Matlab软件对以上两种算法进行仿真研究与对比。仿真时接收信号为线性调频(LFM)脉冲信号[28]，工作频率为20 kHz～ 30 kHz[29]，带宽Bw为10 kHz，中心频率f0为25 kHz，脉宽T为1 ms，基波频率f1为 20 kHz。以一块多通道接收机M=32为例，当期望指向性角度为水平方向0°垂直方向90°时，两种算法的仿真结果如图6所示，其中上三角对应SSB算法，实线为本研究提出的改进算法，虚线为经过低通滤波后输入补偿模块的波形。

图6 算法性能比对Fig.6 Comparison of algorithm performances

为了更加直观地进行比较，图6将两算法的仿真输出幅值同时缩小5倍。两种算法的32路阵子累加结果进行对比可得对应的波形、幅值、以及频率一致且结果完全重合，与单列阵子经过低通滤波后输出的波形相比，幅值明显提高。幅值的增加体现了波束成形空间滤波器的性质，完全重合的结果表明改进算法与传统算法的性能一致。

3 改进算法的FPGA实现

3.1 模块设计与实现

3.1.1 下混频及低通滤波模块

该模块主要由FPGA的直接数字频率合成(DDS)IP核、乘法器以及91阶低通滤波器[30]组成。实现过程中系统时钟为200 MHz，采样时钟为1 MHz。由于下混频包括实部和虚部，因此一个扇区中的32个阵子，在一个采样时钟内将产生64组数据，为节省资源采用64路时分复用。

一个采样周期内，32路各传输一个数字信号，先后与DDS产生的余弦值和正弦值经过乘法器相乘，最后经低通滤波器向时间补偿模块输入一组数据。下一个采样周期时，32路将各传输另一个数字信号值，并按照上述过程向下一级输出另一组数据，以此类推。

3.1.2 时间补偿模块

时间补偿模块状态机如图7所示，分为初始态、实部读取态、虚部读取态、以及返回态。初始态主要判断上一模块输出通道数的高五位与时间补偿模块的对应通道数是否相等。当两者相等且控制信号处在高位时，时移缓冲区的地址写入当前指针值，同时时移缓冲区依次写入上一模块输出数据的实部和虚部。虚部写入完毕后转至实部读取态，当波束计数器小于39 时，状态机跳转至虚部读取态进行地址运算，否则状态跳转至返回态而后回到初始态进行下一个采样时钟的时移计算。

图7 时间补偿状态机Fig.7 State machine of time compensation

3.1.3 相位补偿模块

由相位补偿模块的计算公式可得，算法实现时需要对输入本模块的实部乘上对应的正余弦值。为节省片上资源，只将0°～90°精度为0.1°的900个正弦值sin(2πf0τ)存入只读存储器(rom)中，根据正余弦转化公式，实时计算出相对应的余弦值。最后通过乘法器和加法器按照公式(6)计算出相位补偿模块的输出值。

相位补偿模块的状态机见图8。初始态时上一模块的有效值输出，对应的控制信号置于高位，状态机跳转至下一状态。相位补偿余弦态和正弦态分别利用乘法器完成输入数据的虚部与正弦相乘、实部与余弦相乘，同时在余弦态中，完成上一组输入数据正余弦相乘后的相加，且在正弦态中，当波束计数器大于39时状态跳转至返回态。

图8 相位补偿状态机Fig.8 State machine of phase compensation

3.2 资源消耗对比

若使用传统移边带算法进行FPGA的实现，由于其并行的结构特点，需要例化32个存储器分别计算并输出对应通道的相位补偿数据，每个通道输出40个波形数据。然后将每个采样时钟对应的移项后的数据存入缓冲区，根据时间补偿参数进行地址运算，此时每个通道将产生40个时间补偿模块，需例化40个存储器。每一个时间补偿模块消耗0.5个块随机存储器(BRAM)，故参数补偿部分需要消耗0.5×40×32=640个BRAM。

若使用改进算法进行FPGA的实现，由于采用了时分复用的串行结构，经过下混频模块后的数据先进行时移计算，每个通道对应一个时间补偿模块，每个时间补偿模块串行输出对应的40组移时数据。随后进行移项时只需要实时计算出当前的相位补偿值并串行输出给下一级，不需要占用额外的存储器。此时每路阵子只对应一个时间补偿模块和一个相位补偿模块，且一块多通道接收机在进行补偿计算时只消耗32×0.5=16个BRAM，相较于传统算法而言改进算法节省了更多的BRAM。

改进算法主要优化了实现过程中的资源消耗量，将通过FPGA实现的两种算法的资源消耗量进行对比，由表1可得，查找表(LUTs)、寄存器(Register)的资源消耗变化不大，然而相较于传统算法，改进算法的BRAM消耗量大幅度减小，且随着阵子数量的增加，节约的BRAM数量显著增加，当阵子数为64时节约了近90.6%的BRAM见图9。

表1 两种算法32路阵子的资源消耗对比Tab.1 Comparison of the resource consumption of the two algorithms for 32 arrays

图9 BRAM消耗对比Fig.9 Consumption comparison of BRAM

4 试验测试

为了进一步检验改进算法的波束成形性能，在消声水池中进行了相关试验。综合考虑水池的测试条件，选取圆柱阵的相邻同层的4个阵子，进行波束成形测试。同时为方便观察接收波束成形的效果，采用收发分离的测试方案来搭建测试平台如图10所示，全向发射的换能器和圆柱阵换能器置于消声水池中，入水深度均为2.7 m，两者距离为5.5 m。全向发射的换能器作为LFM信号发射端，连续发射脉冲为1 ms的LFM信号，由圆柱阵换能器接收回波信号。

图10 测试平台Fig.10 Test system

为了测试单个阵子的性能，首先对4个阵子的指向性进行了测试，其指向性见图11，可得试验使用的换能器阵子1开角为82°，阵子2开角为86°，阵子3开角为90°，阵子4开角为78°，且相邻两阵子间夹角约为22°。

图11 阵子指向性Fig.11 Arrays directivity

根据上文扫海方式，主要对-10°、-5°、0°、5°、10°几个特殊的角度进行测试。将四阵子各自对应的指向性作为加挡函数并带入指向性函数[8]即可得到理论结果。最后将测试时采集到的数据与理论结果进行对比，并分析误差。

测试结果见图12，虚线为理论值，实线为实际测量值。当期望指向性为0°时，测量结果与理论结果的主瓣几乎重合，两者指向性均为0°；当期望指向性为5°和-5°时，测试结果的指向性分别为5°和-6°，理论结果的指向性分别为5°和-5°；当期望指向性为10°和-10°时，测试结果的指向性分别为10°、-9°，理论结果的指向性分别为10°、-10.5°。

图12 实测与理论在不同角度的指向性对比Fig.12 Comparison of directivity between test and theory at different angles

根据测量结果可得，当期望指向性角为±5°时，理论和实测的指向性角度大约偏差1°左右，可能是由于测量时伺服机精度不够造成误差。当期望指向性为10°时，旁瓣值高，造成的原因可能是此时的声程差较大，带来的测量误差较大，即当指向性角越向正向偏离0°，声程差越大，对应旁瓣越高。同时本试验所用换能器采用了束控，这也是导致旁瓣较高的原因之一[31]。实测的波束图相较于理论仿真[12]的偏差在合理范围中，进一步证明改进算法与传统移边带[21]算法在性能上的一致。

5 结论

基于传统的移边带波束成形算法原理，改进算法对传统移边带算法的时间补偿和相位补偿模块进行了顺序的调整与改进，将原有资源占用量较大的并行处理优化为串行运算，并结合FPGA的特点利用时分复用的方法降低资源的消耗量，在保留原有算法精度的前提下提高了硬件处理速度，同时节省了硬件的成本。本研究主要考虑了硬件处理方面的资源消耗与波束成形性能之间的关系，要更加直观地观察回波是否击中目标物体，还需要通过上位机的界面显示来实现，然而由于网口传输的数据量有限，因此今后还应对波束成形过程中各个模块的数据进行相应的截位，并对采集到的数据进行分析，以实现在波束成形性能不变的同时，传输更多的数据，从而获得更加清晰的图像。

□