农村垃圾处理PPP项目三方演化博弈分析

周镇浩，王艳伟

(云南农业大学 建筑工程学院，云南 昆明 650201)

0 引 言

改善农村人居环境是实施乡村振兴战略和建设美丽中国的重要组成部分，垃圾处理设施的建设是改善人居环境不可或缺的一环[1].随着农村经济的迅速发展以及城镇化进程的加快，农村垃圾数量逐年递增[2].因此，有效地提高垃圾处理水平，增强农村垃圾处理设施建设迫在眉睫[3].

政府与社会资本方合作模式(Public-Private-Partnership, PPP)[4]是一种公共部门与社会资本方合作提供公共产品或公共服务的模式，由于其能够有效缓解政府部门的财政压力，提供优秀先进的管理经验，在农村基础设施建设方面采用PPP模式是目前一种有效的途径[5].

在PPP项目中由于各方利益需求不同，故而在各个利益相关方之间存在博弈行为，目前有不少学者将博弈论应用于PPP 项目研究.杜杨和丰景春[6]、吴孝灵等[7]都基于Stackelberg 博弈模型研究了 PPP 项目的补偿机制; 王颖林等[8]通过建立政府部门与社会资本方之间博弈模型分析了社会资本方的投机行为;吴凡等[9]利用讨价还价博弈理论对政府和社会资本方进行收益分配，并根据计算结果对项目的特许期进行更为合理的决策.由于传统博弈论假定博弈参与方都具有完全理性，然而人们通过习惯或生活经验去决策，不可能实现博弈论中通过计算得出的最优策略，故而以 Maynard Smith 为代表的理论生物学家提出了演化博弈论，他们通过运用经济学中的博弈框架来分析生物之间的相互依存与斗争，从而将自然选择带来生物演化的思想与博弈论相结合[10].目前国内多名学者对演化博弈的应用进行了广泛研究.薛殿中[11]通过演化博弈探讨了媒体报道策略选择的概率以及媒体不实报道程度对食品安全网络舆情的影响.白璐瑜[12]利用三方演化博弈模型探讨了农产品网络舆情中政府、媒体、网民的行为策略选择及其互相作用关系；田泽等[13]利用演化博弈探讨了政府和企业间双方策略选择的规律；胡振华等[14]基于演化博弈的视角探究 PPP 模式下城市基础设施项目公私双方的合作关系，发现在 PPP 项目中，仅依靠合作双方的自身演化无法达到策略最优解，需要引入监管机制.鉴于此，目前相关研究主要局限于政府、社会资本方两方主体间的博弈，很少对三方演化博弈行为的研究.

在运用PPP模式运营垃圾处理设施的过程中，社会资本方为了追求利益最大化倾向于投机行为[15]，在垃圾处理设施PPP项目的运营过程中，社会资本方的投机行为主要表现在降低运营期间的成本，导致设施质量不过关或提供垃圾处理服务质量下降，最终致使环境污染等一系列有损社会利益的事件发生.为了避免由于社会资本方的投机行为导致出现有损社会利益的事件，政府监管是必然选择.当政府采取监管策略时，会对社会资本方的行为进行实时监控(比如在污水处理 PPP 项目中，通过在线检测设备实时监测经过处理后的出水水质、污泥含水率和尾水排放等指标)[16].当监测发现社会资本方采取了投机行为后，给予社会资本方处罚.叶晓甦和邓云[17]提出PPP项目成功的关键在于政府部门、社会资本方与公众方的合作，建立合理的奖惩制度，优化监督机构，引入公众监督来避免社会资本方采取投机行为.公众参与监督可以通过新闻媒体披露，也可以对PPP项目进行质量追踪与监测，同时也可以向政府部门举报社会资本方采取投机行为.

合理的公众参与监督对于PPP项目的可持续发展有重要意义[18]，因此，政府和社会资本方以及公众之间的利益均衡成为了三者利益博弈的焦点.本研究采用演化博弈模型以及matlab仿真模拟探讨影响政府、社会资本方、公众三方之间博弈稳定性的相关因素.

1 农村垃圾处理设施PPP项目三方演化博弈模型构建

1.1 模型的基本假设

假设2博弈的各参与主体会根据其他方选择的策略来对自身采取的策略进行修改.由于目前我国在农村垃圾处理设施应用PPP模式还处于一个相对发展较低的水平，所以需要政府的补贴和扶持.

假设3政府的策略是积极监管或消极监管.政府采取积极监管的行为概率为x(0≤x≤1),消极监管的概率为1-x.社会资本方的策略是采用积极行为和投机行为.社会资本方采取积极行为的概率为y(0≤y≤1)，采取投机行为的概率为1-y.公众的策略是积极监管或不监管.公众积极监管的概率为z，公众不参与监管的概率为1-z(0≤z≤1).

假设4在博弈过程中，当政府选择积极监管时，会支持社会资本方建设和运营垃圾处理项目，给予财政资助I，若政府的支持力度为α，则社会资本方受到的财政资助为αI，同时会对社会资本方的投机行为进行检查从而给予惩罚M，若惩罚的力度为β，社会资本方受到的惩罚为βM.消极监管的时候只有在公众监督且社会资本方采取投机行为时会给予社会资本方惩罚.当公众采取积极监管的时候政府会给予公众奖励Rp，若奖励力度为γ，公众受到的奖励为γRp.政府选择积极监管获得的收益(政府采取监管时获得的社会评价、上级领导给予的奖励等)为Rg，政府采取积极监管的成本为Cg；政府采取消极监管的成本为Cg′(Cg>Cg′).在运营过程中出现有损社会利益的事件时各个参与方受到的损失为Fp.社会资本方选择积极行为的成本为Ce，若选择投机行为的成本为Ce′(Ce>Ce′)，当政府或者公众发现潜在问题，经检查不合格时检测费用K由社会资本方承担，反之则由政府承担.对于公众而言，积极监管的成本为Cp，来自政府的奖励为Rp，相关参数及含义如表1.

表1 相关参数及含义

1.2 构建收益矩阵

根据上述假设建立收益矩阵如下：

1.3三方演化博弈均衡分析

根据表2中的收益矩阵，可得政府、社会资本方、公众三方主体的期望收益如下：

表2 不同策略组合下的收益矩阵

UA1=yz(Rg-Cg-γRp-K-αI)+y(1-z)(Rg-Cg-K-αI)+(1-y)z(Rg-Cg-γRp+βM)+(1-y)(1-z)(Rg-Cg+βm)

(1)

UA2=yz(-Cg′-γRp-K)+y(1-z)(-Cg′)+(1-y)z(-Cg′-γRp+βm)+(1-y)(1-z)(-Cg′-Fp)

(2)

(3)

UB1=xz(αI-Ce)+x(1-z)(αI-Ce)+(1-x)z(-Ce)+(1-x)(1-z)(-Ce)

(4)

UB2=xz(-Ce′-βM-K)+x(1-z)(-Ce′-βM-K)+(1-x)z(-Ce′-K-βm)+(1-x)(1-z)(-Ce′-Fp)

(5)

(6)

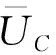
UC1=xy(γRp-Cp)+x(1-y)(γRp-Cp)+(1-x)(1-y)(γRp-Cp)+(1-x)y(γRp-Cp)

(7)

UC2=(1-x)(1-y)(-Fp)

(8)

(9)

三方博弈主体的复制动态方程和演化稳定性分析：

基于复制动态方程原理，根据式(1)和式(2)构造出政府采取积极监管策略的复制动态方程为：

(10)

1)当z=a时，F(x)≡0表明所有的策略都是稳定状态，即此时的策略选择比例不会随着时间的推移而变化，该博弈处于稳定状态.

根据式(4)和式(5)可构建社会资本方采取积极策略的复制动态方程为：

=y(1-y)[Fp+Ce′-Ce+zk+zβm-zFp+x(βm+k-Fp+zFp-zk-zβm)]

(11)

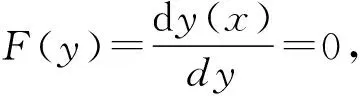
1)当x=b时，F(y)≡0，此时所有的策略选择比例都是稳定状态，即此时的策略选择比例不会随着时间的推移而变化.

根据式(7)和式(8)可构建公众采取参与监督策略的复制动态方程为：

(12)

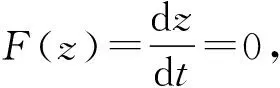
1)当y=c时，F(z)≡0，此时所有的策略选择比例都是稳定状态，即此时策略选择比例不会随着时间的推移而变化.

2 三方演化博弈系统的均衡分析

在讨论了政府、社会资本方、公众三方博弈行为的复制动态行为后对整个演化博弈系统进行均衡分析.

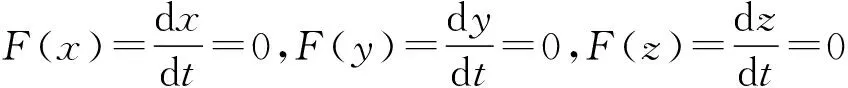
根据Friedman[20]提出通过分析系统的雅可比矩阵来判断均衡点的稳定性，求解式(10)、式(11)、式(12)的关于x、y、z的偏导得到雅可比矩阵.

由于只需要讨论纯策略的纳什均衡解(系统均衡点的渐进稳定性).

由动力系统理论可知，任何线性系统的解的稳定性问题都可以化为对应的线性齐次系统的零解的稳定性问题[21].对于线性齐次常系数系统x=Ax(t∈-∞,+∞),x∈Rn，A为n*n常值矩阵，其零解是局部稳定的必要充分条件是A的一切特征值都是负实部[22].

由上述文献分析可得判断某纯策略的纳什均衡解的渐进稳定性只需要将该点代入判断雅可比矩阵的特征值符号.

博弈系统在(0,0,0)时的雅可比矩阵为：

此时特征值λ为：

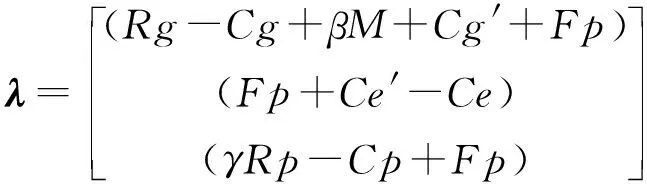
若同时满足(Rg-Cg+βM+Cg′+Fp)<0,(Fp+Ce′-Ce)<0,(γRp-Cp+Fp)<0,此时(0,0,0)是渐进稳定点.

博弈系统在(0,0,1)时的雅可比矩阵为：

此时特征值λ为：

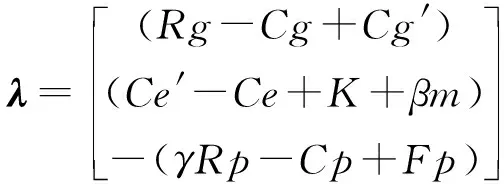
若同时满足Rg-Cg+Cg′<0,(Ce′-Ce+K+βm)<0,-(γRp-Cp+Fp)<0,此时(0,0,1)是渐进稳定点.

博弈系统在(0,1,0)时的雅可比矩阵为：

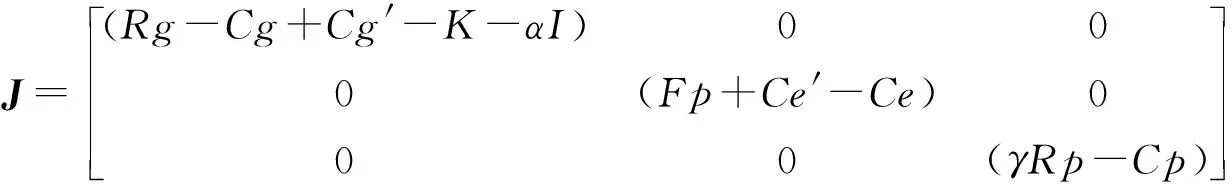
此时特征值λ为：

若同时满足(Rg-Cg+Cg′-K-αI)<0,-(Fp+Ce′-Ce)<0,(γRp-Cp)<0,此时(0,1,0)是渐进稳定点.

博弈系统在(1,0,0)时的雅可比矩阵为：

此时特征值λ为：

若同时满足-(Rg-Cg+βM+Cg′+Fp)<0，(Ce′-Ce+K+βm)<0,(γRp-Cp)<0,此时(1,0,0)是渐进稳定点.

博弈系统在(1,1,0)时的雅可比矩阵为：

此时特征值λ为：

若同时满足-(Rp-Cg+Cg′-K-αI)<0,(Ce′-Ce+K+βm)<0,(γRp-Cp)<0,此时(1,1,0)是渐进稳定点.

博弈系统在(1,0,1)时的雅可比矩阵为：

此时特征值λ为：

若同时满足-(Rg-Cg+Cg′)<0,(Ce′-Ce+K+βm)<0,-(γRp-Cp)<0, 此时(1,0,1) 是渐进稳定点.

博弈系统在( 0,1,1)时的雅可比矩阵为：

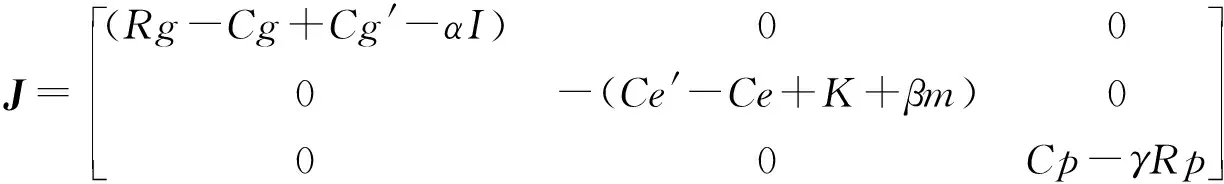
此时特征值λ为：

若同时满足(Rg-Cg+Cg′-αI)<0,-(Ce′-Ce+K+βm)<0,Cp-γRp<0,此时(0,1,1)是渐进稳定点.

博弈系统在(1,1,1)时的雅可比矩阵为：

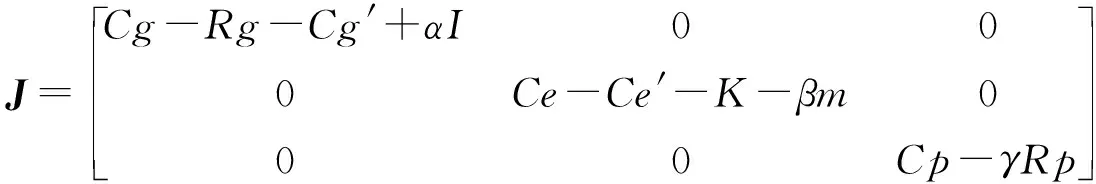
此时特征值λ为：

若同时满足Cg-Rg-Cg′+αI<0,Ce-Ce′-K-βm<0,Cp-γRp<0,此时(1,1,1)是渐进稳定点.

综上所述各个平衡点的渐进稳定性如表3所示.

表3 各平衡点的渐进稳定性

3 仿真模拟

3.1 策略初始值变化模拟

根据得到的复制动态方程,运用matlab软件模拟仿具体的政府-社会资本方-公众三方演化博弈，部分数值来自于广州番禺垃圾焚烧发电厂案例[23],根据本研究需要以及农村垃圾处理设施PPP项目三方演化博弈的实际情况进行调整.

各参数设为Ce= 33，Ce′ = 25，K=1.5，Rg= 18，Cg= 17，Cg′ = 13，Rp= 12，Cp= 5，Fp= 12，I=19,α=0.5,M=20,β=0.5，γ=0.5.

各方策略的初始值不同的情况下演化结果如图1所示.x取值范围为(0,1)，y取值范围为(0,1)，z取值范围为(0,1).

图1 不同策略初始点演化博弈图Fig.1 Evolutionary game diagram of the initial point of different strategies

X、Y、Z三轴为政府、社会资本方、公众三方策略选择的概率.由图可见无论初始值选择如何变化，最后系统总是趋近于点(1,1,1)，由此说明在此系统中(1,1,1)为唯一稳定点，即政府会采取监管的策略，社会资本方会采取积极行为的策略，公众会采取积极监管的策略.

3.2参数变化模拟

基于matlab软件进行仿真模拟，根据分析结果，讨论政府对于社会资本方的帮扶力度(α)、政府对于社会资本方选择投机行为的惩罚力度(β)、公众积极监管时政府奖励力度(γ)对系统稳定性的影响.由于在(1,1,1)点的雅可比矩阵的特征值为Cg-Rg-Cg′+αI、Ce-Ce′-K-、Cp-γRp，即代表了在均衡点(1,1,1)α的变化只对x，即政府方的策略产生影响，β的变化只对y社会资本方的策略产生影响，γ的变化只对z公众方的策略产生影响.因此探讨政府对于社会资本方的帮扶力度(α)、政府对于社会资本方选择投机行为的惩罚力度(β)、公众积极参与时政府奖励力度(γ)对系统稳定性的影响只需要分别讨论α对政府方决策的影响、对社会资本方决策稳定性的影响，γ对公众决策稳定性的影响.

3.2.1 政府对社会资本的帮扶力度

α取值为0.2、0.4、0.6、0.8、1分别对应低帮扶标准、中低帮扶标准、中等帮扶标准、中高帮扶标准以及高帮扶标准.

由上述模拟可知初始点的选择不会对系统稳定性产生影响，本文选择1/3为初始策略点探讨α政府对于社会资本方的帮扶力度对于政府方决策的影响.对应的演化博弈结果见图2.

图2 不同帮扶力度对政府方决策的影响Fig.2 The impact of different levels of assistance on government decision-making

由图可得当α的取值为1，即高强度补贴时会吸引社会资本方的加入使得政府短期内提升积极监管的策略选择意愿，但后期政府会因为财政压力过大导致选择消极监管的策略；过高强度的补贴会导致政府选择消极监管策略.

3.2.2β政府对社会资本方选择投机行为的惩罚力度

β取值为0.2、0.4、0.6、0.8、1分别对应低惩罚标准、中低惩罚标准、中等惩罚标准、中高惩罚标准以及高惩罚标准.本文选择1/3为初始策略点探讨β政府对社会资本方选择投机行为的惩罚力度对于社会资本方决策的影响.对应的演化博弈结果见图3.

图3 不同惩罚标准对社会资本方策略选择意愿影响Fig.3 The impact of different punishment standards on the willingness of social capital to choose strategies

由图3可知，当β取值为0.2时，即低惩罚标准时社会资本方就会选择投机行为，同时可以看出高的惩罚标准会加快社会资本方选择积极行为；过低的惩罚力度会导致社会资本方做出投机行为的决策.

3.2.3γ公众积极参与时政府奖励力度

γ取值为0.2、0.4、0.6、0.8、1分别对应低奖励标准、中低奖励标准、中等奖励标准、中高奖励标准以及高奖励标准.本文选择1/3为初始策略点探讨γ政府对于公众参与的奖励力度对公众决策的影响.对应的演化博弈结果为图4.

图4 不同的奖励力度对公众方策略选择意愿的影响Fig.4 The impact of different rewards on the public’s willingness to choose strategies

由图4可知，当选择中低奖励力度或者中等奖励力度都会导致公众方选择不监管的意愿.由于政府补贴的形式新颖，在选择中低奖励力度时可能对短期提高公众方选择积极监管的意愿有帮助，但是后期因为过低的补贴会导致公众方选择不监管；过低的补贴力度会导致公众做出不监管的决策.

4 结论及启示

本文利用有限性理性原则，建立了农村垃圾处理设施PPP项目的演化博弈模型，结合了matlab软件模拟仿真了政府、社会资本方以及公众在项目建设运营中的博弈行为.研究表明：

在政府积极监管获得的收益大于两种策略的成本差加上对企业的资助，同时社会资本方两种策略的成本差小于检查成本加上政府对社会资本方投机行为的惩罚，以及政府对公众参与监督的奖励大于公众参与监督的成本时，系统会趋于(1,1,1)的稳定状态，即政府会选择积极监管，社会资本方会采取积极行为，公众会积极参与.

对于政府而言选择高补贴力度并不会提高社会资本方选择积极监管的意愿，反而会因为过高的补贴力度会导致政府选择消极监管.当政府采取低等级的惩罚时会因为社会资本方的天然逐利性导致社会资本方采取投机行为，提高惩罚力度会导致社会资本方采取积极行为的意愿提升.对于公众而言，低等级以及中低等级的奖励力度都会导致公众参与意愿下降.

由研究结论，得到以下启示：

1)县级政府部门应当加大对于农村垃圾处理设施PPP项目的推进，同时提高对建设完成以及在建垃圾处理设施的乡镇政府部门的嘉奖.此外，乡镇政府应当优化管理结构，引入管理人才，降低政府监管社会资本方的成本；

2)由于农村垃圾处理设施对社会资本方缺乏吸引力，适当的补贴可以提高社会资本方参与投资的意愿.同时应当注意过高的补贴会导致政府财政压力过大，所以需要将补贴控制在一个适当的范围；

3)政府加大对社会资本方采取投机行为的处罚力度，会提高社会资本方采取投机行为所付出的成本，可以有效地降低社会资本方采取投机行为的意愿.政府应当加大对社会资本方采取投机行为的处理力度；

4)提高补贴力度可以加强公众参与监督的意愿，为了提高公众参与监督的意愿，政府加大公众参与监督的意愿，政府应当加大对公众参与监督补贴的力度.

本文基于演化博弈理论和matlab工具建立了农村垃圾处理设施PPP项目演化博弈模型，通过研究结论提出了相关建议，但由于演化博弈的收益矩阵所限，未能将影响模型的情况考虑完善，比如补贴力度对于社会资本方的吸引，以及惩罚力度对社会资本方参与意愿的影响，这正是今后研究的重点.