玻璃微珠/环氧树脂复合泡沫材料的力学性能及其理论分析

王 杰,郭行洪,王 俊

(南京工业大学土木工程学院,江苏南京 211800)

1 前 言

以空心玻璃微珠（hollow glass microsphere,HGM）填充聚合物基体制备而成的复合泡沫材料,由于空心微珠独特的闭孔结构,使得微珠泡沫材料相比于传统泡沫材料具有低密度、高比强度和刚度、低吸湿性和相当高的热稳定性,被广泛应用于轻质高强夹芯材料、航天工业领域的结构构件、阻尼板材、浮力材料和隔热材料[1-4]。空心微珠种类繁多,如玻璃微珠、碳微珠、陶瓷微珠、聚合物微珠和金属微珠。环氧树脂（epoxy resin,EP）、酚醛树脂、聚酯树脂、聚氨酯、有机硅等都是常见的基体材料[5-6]。

不同组分的微珠泡沫体现出不同的力学性质。Gupta等[7]研究了不同壁厚和密度的空心微珠对复合泡沫拉伸和压缩性能的影响,微珠体积填充量由30%增至60%时尽管强度和模量呈减小趋势,但压缩比强度和比模量却逐渐增加；Zhang和Ma[8]通过改变空心微珠的含量,讨论了酚醛复合泡沫压缩和弯曲强度的变化,微珠含量的增加减弱了微珠与基体间的界面黏结性从而导致压缩强度及弯曲强度的降低；Wang等[9]研究了空心微珠/环氧树脂泡沫材料的压缩性能,发现复合泡沫材料的压缩强度和模量与其密度呈幂次定律关系。Nian 等[10]对空心微珠/环氧树脂泡沫的失效行为进行了分析并使用有限元模型进行了模拟,结果表明,复合泡沫的拉伸强度随着壳厚度的增加而增加；Wouterson等[11]对含有空心玻璃微珠和酚醛微珠的复合泡沫材料的断裂韧性进行了研究,与酚醛微珠相比,空心玻璃微珠具有更高的断裂韧性；随着微珠体积分数的增大,断裂韧性下降,主要原因是微珠和树脂基体的剥离导致应力集中及过早的裂纹。

现有研究都侧重于复合泡沫材料的静力性能,对复合泡沫材料的低速冲击性能和理论研究较少。本研究设计并制备了空心玻璃微珠（HGM）/环氧树脂（EP）复合材料,分析了HGM 的含量对复合材料抗压强度、拉伸强度以及冲击性能的影响,并结合SEM 图像分析其影响机制。通过夹杂方法将宏观的微珠泡沫用细观力学来预测其有效模量,为实际工程应用提供理论支持。

2 实 验

2.1 主要原料

微珠泡沫复合材料的基体采用惠柏新材科技（上海）股份有限公司生产的双酚A 型环氧树脂（GE-7118A）和固化剂（GE-7114B）,其中环氧值约为0.57 eq/100 g、胺值约为565 mg KOH/g；3-氨基丙基三乙氧基硅烷（KH550）由上海源叶生物科技有限公司供应；HGM 由美国3M 公司供应,密度为0.25 g/cm3,粒径为55μm,壁厚为2μm,抗压强度为5.2 MPa。

2.2 试件制备

将EP和固化剂按2∶1体积比配置。浇筑试件时,先将EP和固化剂放在75 ℃的油浴锅里加热以降低其稠度,待到两者充分稀释、流动性好时加入经偶联剂处理过的HGM,在55℃油浴条件下搅拌30 min。采用注模成型工艺制备微珠泡沫复合材料,在室温固化24 h后脱模。分别设计了微珠体积分数为50%、70%和75%的试件,所对应的理论密度分别为725、535 和487 kg/m3,编号分别为G50、G70和G75,其中G 表示试件中含有空心玻璃微珠,后面的数字表示加入空心玻璃微珠的体积分数。复合泡沫材料示意如图1所示。

图1 微珠泡沫复合材料示意Fig.1 Schematic diagram of microspheres in syntactic foam composites

2.3 试验方法

压缩试验在600 k N 的万能试验机上进行。参考ASTM D1621-10[12]标准。试件尺寸为100 mm×100 mm×50 mm,每组试样取5个平行试块。试块侧面中心位置处各贴一个应变片,采用2 mm/min 的速率连续加载。

拉伸试验在300 k N 的万能试验机上进行。参考ASTM D638-02a[13]标准。试件尺寸为165 mm×19 mm×5 mm,每组试件取5个平行试件。两端粘贴铝片保证试件拉伸时端部不会被夹具夹坏。试件中部粘贴横向和竖向应变片各一个,以测量拉伸应变和泊松比,加载速率为3.75 mm/min。

低速冲击试验在落锤式DTM1203低速冲击试验机上进行。参考ASTM D7136/D7136M-2005[14]标准,试验装置如图2所示。低速冲击试验机的冲击锤头质量为5.5 kg,冲击头为直径16 mm 的半球体。试件尺寸为150 mm×100 mm×20 mm 的微珠泡沫板,每种微珠体积含量取3 个平行试件,在0.8、0.9 和1.2 m 三种不同的冲击高度下进行试验,冲击能量分别为43、49和65 J,对应的冲击速度为3.96、4.20和4.85 m/s,记为Ⅰ、Ⅱ、Ⅲ。

图2 低速冲击试验装置Fig.2 Low velocity impact test set-up

3 结果与讨论

3.1 复合泡沫材料静力性能

微珠泡沫的压缩破坏可归纳为三个阶段——线弹性阶段、塑性变形阶段和压缩密实破坏阶段（图3）。在线弹性阶段,结合表1可以得出,复合泡沫G50比G70的抗压强度和压缩模量分别提高了132%和86%；G50比G75的抗压强度和压缩模量分别提高了185%和120%。可知,随着微珠体积分数的增加,复合泡沫的压缩强度和压缩模量呈减少的趋势。减少的趋势表明,当微珠体积分数增加时,体系中引入了更多的空心体积,在降低材料绝对质量的同时也降低了材料的压缩强度。在塑性变形阶段,压缩强度略有下降,其原因是空心微珠在树脂基体内产生破裂。当大量空心微珠被压碎和压实时,荷载的进一步增加导致复合泡沫的致密化,材料进入压缩密实破坏阶段。

图3 压缩应力-应变曲线Fig.3 Curves of compressive stress-strain

根据图4可以看出,拉应力随着拉应变线性增大,到达峰值后突然破坏,呈现出明显的脆性断裂特征。结合表1可知,复合泡沫G50比G70的抗拉强度和拉伸模量分别提高了24%和23%；G50 比G75 的抗拉强度和拉伸模量分别提高了65%和42%。图5分别给出了微珠体积分数为70%和75%的微珠泡沫拉伸断面SEM 照片。如图5（a）所示,玻璃微珠和树脂基体间的强结合力阻碍了微裂纹的扩展,使其朝不同方向发展而形成“褶皱状结构”,这种褶皱结构可以吸收额外的断裂能量,保证复合泡沫具有一定的拉伸强度。随着微珠体积分数的增大,单位体积内树脂含量降低,两者之间的界面作用减弱,过多的微珠在树脂基体中发生团聚（图5（b））,产生应力集中,从而使其拉伸强度降低。

图4 拉伸应力-应变曲线Fig.4 Curves of tensile stress-strain

图5 微珠泡沫拉伸断面SEM 照片Fig.5 SEM images of microspheres syntactic foam tensile specimens

表1 不同微珠含量微珠泡沫复合材料的拉伸和压缩性能Table 1 Microspheres syntactic foam static performance

3.2 复合泡沫材料冲击性能

试件的冲击荷载曲线显示出类似的半正弦曲线（图6及图7）。对比冲击能量相同,微珠体积比不同的试件（G50-Ⅲ,G70-Ⅲ,G75-Ⅲ）（图6）,结合表2,以G50-Ⅲ为参考对象,G70-Ⅲ和G75-Ⅲ冲击力峰值分别降低了21%和30%,吸收能量分别降低了7%和19%,而冲击作用时间分别增加了9%和19%,凹陷深度分别增加了24%和35%,比吸能（SEA）分别增大了29%和21%。上述性能变化表明随着微珠体积分数的增加,材料整体刚度和冲击力峰值有所降低,而冲击作用时间和凹陷深度随之增大,其中体积分数为70%的微珠泡沫板在65 J时SEA最大,吸能效果最好。

图6 不同微珠体积分数泡沫板冲击荷载-时间曲线Fig.6 Impact load-histories of syntactic foams with different microspheres volume fraction

图7 G70微珠泡沫板冲击荷载-时间曲线Fig.7 Impact load-histories of G70 microspheres syntactic foam plate

表2 微珠泡沫板低速冲击试验结果Table 2 Impact test results of syntactic foam

从图8（a）可以看出空心玻璃微珠在环氧树脂基体中较均匀,并且每一颗空心玻璃微珠都被环氧树脂浸润包围,具有很好的粘结效果。在冲击能量为65 J时,G70-Ⅲ中的空心玻璃微珠被冲击能量完全冲碎且环氧树脂也在冲击后表面出现碎裂,紧密粘结的微珠和树脂在受到冲击能量后微珠因受到冲击而破碎的同时树脂作为缓冲基体将能量卸去（图8（b））；G75-Ⅲ相对于G70-Ⅲ冲击面后的微珠有少部分并没有破碎,表明随着微珠体积分数的增大,过多的微珠在树脂基体中会发生团聚,影响微珠泡沫板的吸能效应（图8（c））。

图8 微珠泡沫板低速冲击SEM 照片 （a）G70-Ⅲ冲击前的冲击面；（b）G70-Ⅲ冲击后的冲击面；（c）G75-Ⅲ冲击后的冲击面Fig.8 SEM images of syntactic foam board low velocity impact （a）impact surface before G70-Ⅲimpact；（b）impact surface after G70-Ⅲimpact；（c）impact surface after G75-Ⅲimpact

对比微珠体积比相同,受到冲击能量不同的试件（G70-Ⅰ,G70-Ⅱ,G70-Ⅲ）（图7）,结合表2,以G70-Ⅰ为参考对象,G70-Ⅱ和G70-Ⅲ冲击力峰值分别增加了9%和37%,冲击作用时间分别增加了7%和14%,凹陷深度分别增加了18%和26%,冲击能量分别增加了21%和64%,SEA 提高了18%和64%。上述性能变化表明随着冲击能量的增大微珠泡沫板的碰撞接触时间稍有增大,冲击力峰值也会上升,吸收能量增加,比吸能也同样提高。

3.3 微珠泡沫复合材料有效模量预测理论值与试验值对比

根据复合材料细观力学的理论,由椭球型夹杂理论可以得出球型夹杂理论公式[15]:

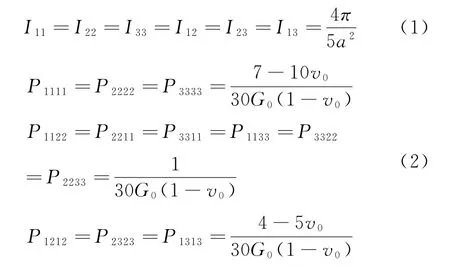
式中:I i是椭球型夹杂形状的相关常数,I ij由I i确定,P injp由I ij和I i确定,v0是泊松比。

对于球型夹杂,各向同性张量P只有两个独立分量,用体积和剪切模量来表示泊松比:

式中:G0为基体的剪切模量,K0为基体的体积模量。

则球型夹杂张量B的表达式为:

式中:K1为夹杂的体积模量,G1为夹杂的的剪切模量；并且有:

依据试验试件的材性参数代入上述公式中,可得表3理论值与试验值进行比较。

由表3可知,只加入空心玻璃微珠的微珠泡沫误差较小,在10%左右,属于试验过程中不可避免误差,所以理论值与试验值较为吻合。

表3 微珠泡沫有效模量理论值与试验值对比Table 3 Comparison of theoretical and experimental values of effective modulus of microbeads

4 结 论

研究了空心玻璃微珠/环氧树脂复合泡沫材料在不同玻璃微珠体积分数下的力学行为,得到如下结论:

1.当微珠体积含量从50%增加到75%时,微珠泡沫的抗压强度和模量分别降低了65%和55%,抗拉强度和模量分别降低了39%和30%。空心玻璃微珠含量增大有助于减轻复合泡沫的密度,但过多的玻璃微珠在树脂基体中易发生团聚,材料之间界面作用减弱,脆性增强,导致强度和模量降低。

2.在相同冲击能量下,随着微珠体积比的增大,复合泡沫的冲击接触时间和凹陷深度随之增大,而冲击力峰值和吸收能量随之减小,并且体积分数为70%的微珠泡沫在65 J时SEA 最大,吸能效果最好；随着冲击能量的提高,复合泡沫SEA 整体呈增大趋势。

3.基于复合材料细观模型,通过夹杂方法得出考虑微珠体积分数的模量理论计算公式。理论预测值与试验结果吻合较好。