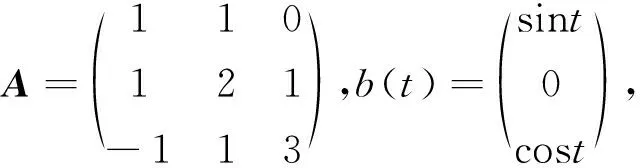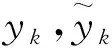常微分方程波形松弛方法的收敛稳定
范振成
(闽江学院 数学与数据科学学院, 福建 福州 350108)
在芯片(大规模集成电路)设计领域, 仿真计算作用重大。 描述芯片的数学模型一般是高维的微分代数方程组, 使用诸如线性多步法和Runge-Kutta方法等经典数值方法进行仿真计算时, 因其计算量太大, 效果不理想。 描述芯片的高维微分代数方程组, 一般是由若干联系微弱的小方程组构成, 针对这个特点, 基于解代数方程组的迭代法, Lelarasmee等[1]提出了解微分方程的波形松弛(WR)方法, 其基本想法是先利用迭代技术将大系统分成若干独立的小系统, 然后根据各小系统的特点选用适合的经典数值方法进行求解计算。与经典方法相比, 波形松弛方法因具有并行性和多速率两个优点, 而更具优势。当实际计算时, WR方法的初始值和中间过程不可避免存在误差, 因此研究误差的传播规律(即稳定性)是有意义的。
对WR方法的研究集中于收敛性, 稳定性的研究不多见。Bellen A等[2]和范振成[3]专注于数值方法是否保持解析解的性质, 给出了离散WR方法的压缩或绝对稳定条件。考虑初值和过程误差是否可控问题, 范振成[4]提出了连续WR方法的收敛稳定, 给出了泛函微分方程波形松弛方法收敛稳定的条件。然而文献[4]中的条件较严格, 很多常见情形不满足。本文将证明在标准的Lipschitz条件下, 常微分方程初值问题的WR 方法是收敛稳定的。
1 假设与准备
对泛函微分方程
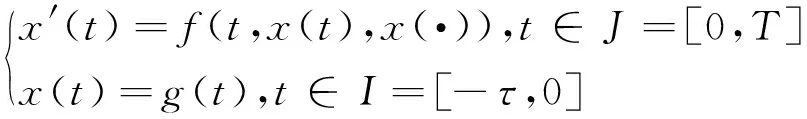
(1)
的连续WR方法(下文简称WR方法)

(2)
其中,分裂函数F(t,x,x,y(·))=f(t,x,y(·)), 初始解x0(t)=g(t),t∈I,k=0,1,…。文献[4]证明了当F满足单边Lipschitz条件(H1)和全局Lipschtiz条件(H2) 时,F和g的微小变化所引起的解序列{xk}变化可控,文献[4]中称之为收敛稳定, 说明了WR方法具有较强的抗干扰能力。然而文献[4]中的条件(H1)较严格, 很多常见情形不满足(H1)。
考虑常微分方程的初值问题
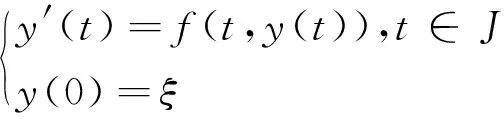
(3)
及其WR方法

(4)
其中,y,yk∈C1(J,Rn),F(t,x,x)=f(t,x)。此处和下文用Rn表示n维实数域,R表示实数域,R-表示负实数集,R+表示正实数集,C1(J,Q)表示区间J到数集Q上有一阶连续导数的函数集,C(J,Q)表示J到Q上连续函数集。
假设分裂函数满足以下两个Lipschitz条件:

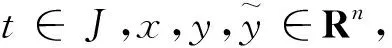
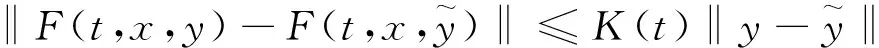
其中,〈·,·〉:Rn×Rn→R表示内积,‖x‖=〈x,x〉1/2。
此时,文献[4]的结果变成:当(H3)和(H4)成立时, WR方法式(4)是收敛稳定的, 即式(4)与其扰动系统

(5)
解的差满足:存在C>0使得
由于条件(H3)中的m(t)<0, 这是较严格的限制, 排除了诸如F(t,x,y)=x+y等常见情况, 考虑更宽松的标准Lipschitz条件:

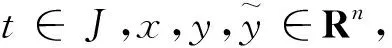
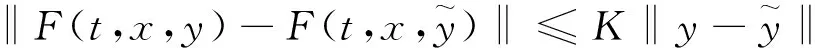
式中,L可以取正数, 因此(H1′)比(H3)更宽松, 在(H1′)使用L∈R而不是更简单的L>0, 只是为了扰动解的误差上限更准确, 后文将推出其与L+K有关, 见式(8)。此外, 若(H4)成立, 则(H2′)成立, 这说明(H2′)比(H4)更宽松。
本文将证明当(H1′)和(H2′)成立时, WR方法(4)是收敛稳定的。首先证明两个引理。
引理1 .1当(H1′)和(H2′)成立时, WR方法式(4)产生的函数序列{yk}收敛于式(3)的解, 即
证明:由文献[5]中定理7.3 或式(7.15), 易知本引理成立。
引理 1.2 假设u∈C1(J,R+),v∈C(J,R+),L1≠0,L2>0,γ1>0,γ2>0且
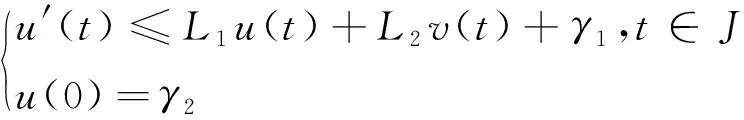
(6)
若存在γ≥max{γ1,γ2},V∈C(J,R+),U∈C1(J,R)满足V(t)>v(t),t∈J和
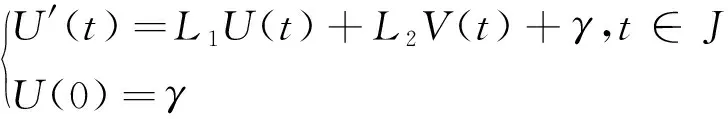
(7)
则U(t)≥u(t),t∈J。
证明:式(7)减式(6)得
两边乘以e-L1t得
(e-L1t(U(t)-u(t)))′≥
e-L1tL2(V(t)-v(t))+e-L1t(γ-γ1)
两边从0到t积分得
e-L1t(U(t)-u(t))≥γ-γ2+
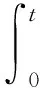
由引理条件, 上式右端大于零, 因此U(t)≥u(t),∀t∈J. 证毕。
2 主要结果
定理2.1当(H1′)和(H2′)成立时, WR方法式(4)是收敛稳定的, 即式(4)和它的扰动系统式(5)生成的函数序列满足:
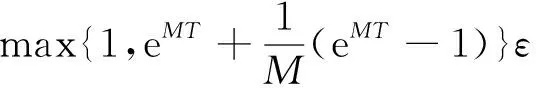
(8)


由此式和内积的性质, 得
由上式, (H1′)、 (H2′) 以及Cauchy-Schwarz不等式, 推导出
〈ηk+1(t),ηk+1(t)〉′≤2L‖ηk+1(t)‖2+
2K‖ηk+1(t)‖‖ηk(t)‖+2‖ηk+1(t)‖‖δk+1(t)‖
(9)
另一方面
〈ηk+1(t),ηk+1(t)〉′=(‖ηk+1(t)‖2)′=
2‖ηk+1(t)‖(‖ηk+1(t)‖)′
(10)
由式(9)和(10)得
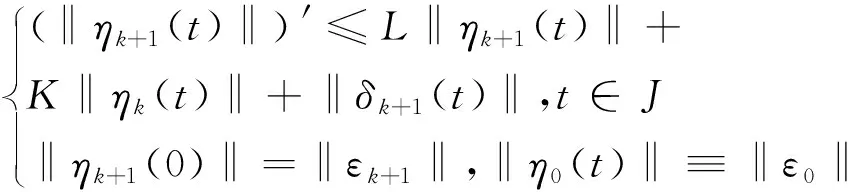
(11)

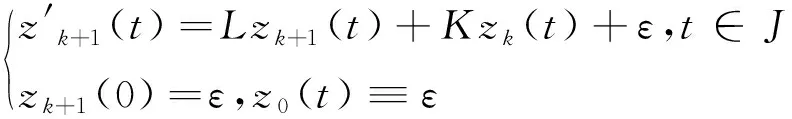
(12)
由式(11) (12)和引理1.2, 不难证明
‖ηk(t)‖≤zk(t),∀t∈J,∀k=0,1,…
(13)
又由引理1.1, (12)生成的函数列收敛于下面微分方程的解
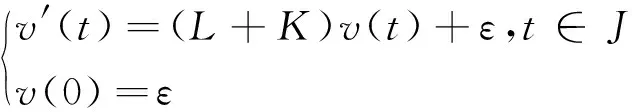
(14)
即
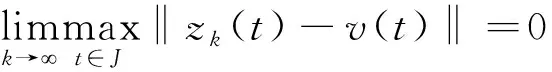
(15)
由式(13)(14)和(15), 易得
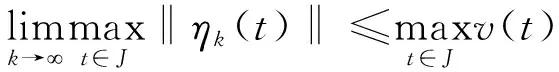
(16)
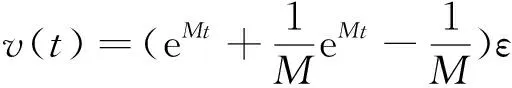
3 定理应用
对于WR方法式(4), 若已知yk时, 能够准确算出yk+1, 则得到的函数序列{yk}的极限为式(3)的解(引理 1.1)。然而, 对大多数方程, 这是不可能的, 一般利用数值方法和插值求近似等于yk+1的函数。常用的离散WR方法的算法如下:

第2步:选择适当的数值方法计算方程
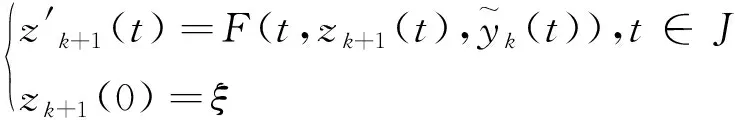
(17)
在节点{0=t0 第4步:k=k+1, 转第2步重复计算, 直至收敛为止。 注意式(17)等价于 (18) 当(H1′)和(H2′)成立时, 由引理1.1和定理2.1, 知存在C>0使得 其中,y是方程(3)的解。 考虑方程(3)至方程(5), 选取f(t,y)=Ay+b(t),其中 J=[0,1],ξ=(1,0,1)T (19) 为了简单,选固定扰动δk(t)≡δ,εk≡ε。使用Jacobi分裂函数, 即 F(t,x,y)=A1x+A2y+b(t) (20) 表1 满足(19)(20)的方法(4)的不同扰动引起的误差uk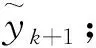

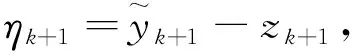
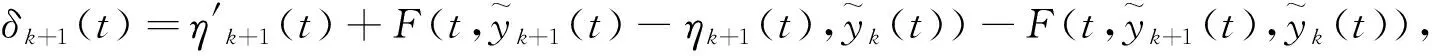
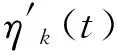
4 数值实验