无线传感器网络的改进DV-hop定位算法研究

周 凯，周培钊，付文涵，魏胜非

(东北师范大学物理学院，吉林 长春 130024)

0 引言

无线传感器网络(Wireless Sensor Networks，WSN)是被人为随机部署在需要检测区域的大量节点通过自组织(ad-hoc)而组成的网络.随着经济的发展和科技的创新，无线传感器网络得到了较大的发展，其在家居生活、军事战场、工业制造等领域的应用变得越来越广泛，其中节点定位算法作为无线传感器网络的一个重要应用，受到了国内外学者的广泛关注.

无线传感器网络定位指的是针对网络中未知节点位置的确定，主要是采用已知锚节点的位置来估计未知节点和剩余节点的距离以及跳数[1].目前，节点定位技术日益成熟，根据是否借助距离信息将其分为两种[2]，分别为需要测距的定位算法和非测距的定位算法.需要测距的定位算法主要是借助外部硬件设备得到节点与节点之间的距离信息，常见的测距定位算法有到达时间(Time of Arrival，TOA)、到达时间差(Time Difference of Arrival，TDOA)、到达角度(Angle of Arrival，AOA)、接收信号指示强度(Received Signal Strength Indication，RSSI)等；非测距的定位算法主要是通过已知位置的锚节点确定未知节点的位置，常见的非测距定位算法有近似三角形测试算法(Approximate PIT Test，APIT)、距离向量跳跃算法(Distance Vector Hop，DV-hop)等.

测距定位算法测得的距离虽然比较准确，但是需要额外的外部设备，对于电池体积较小的传感器节点来说负担较重，这无疑会减少传感器节点的工作时间，降低无线传感器网络的网络寿命；非测距的定位算法虽然定位精度不如非测距算法，但是不需要外部设备的支持[3]，无形之中降低了成本，减少了能量的消耗.

DV-hop算法作为非测距算法中的典型代表成为国内外研究的热点，该算法受环境的影响较小，不需要额外的硬件设备支持，所以适应于成本低、规模大、节点配置简单的无线传感器网络[4].针对DV-hop算法的定位缺陷，国内外很多学者对该算法进行了改进，文献[5]在进行未知节点定位时，使锚节点先后采用两个通信半径广播自身信息，从而获得未知节点与锚节点更准确的跳数，得到未知节点更精确的坐标；文献[6]主要对传统DV-hop算法中的跳数和跳距进行改进，首先将锚节点的通信半径拆分为4个通信半径，分别进行以相应的通信半径进行广播，获得较精确的跳数，同时与未知节点临近的锚节点的跳距都会根据到待定位节点的跳数而产生一个权值，从而产生新的跳距，参与到后续的计算过程中；文献[7]主要针对DV-hop算法平均跳距误差较大的问题，将参与未知节点定位的锚节点的平均跳距按跳数进行分配加权系数，使得后续的计算过程误差更小；文献[8]首先利用节点的通信半径与影响节点跳数的相关参数对全局跳数值进行协同优化，以使节点间的跳数趋于合理，然后根据最佳指数的最小均方误差准则计算平均跳距，并与单跳平均误差共同修正平均跳距，从而进一步降低平均跳距的误差；文献[9]首先基于信标节点估计距离与真实距离的差值，提出了一种全网络的有效跳距，其次在信标节点与未知节点间多跳计算过程中增添了修正值，最后利用列文伯格-马夸尔特算法估计未知节点的最优位置，有效地提高了算法的定位精度.

本文主要研究DV-hop节点定位算法，通过分析传统DV-hop算法的误差，纠正节点之间的跳数以及修正未知节点与锚节点之间的跳距，使得跳数与跳距更加趋于合理化，最后利用改进的最小二乘法进行计算，进一步提升了未知节点的定位精度.

1 传统DV-hop定位算法与误差分析

1.1 传统DV-hop算法定位算法原理

DV-hop算法中主要将节点分为锚节点与未知节点，锚节点在整个网络中占有一定的比例，因为锚节点本身带有GPS定位系统，而未知节点本身不具有定位系统，所以该算法主要利用待定位节点与锚节点的跳数与跳距来计算两者之间的距离，该算法主要分为3个步骤，分别为确定最小跳数、计算未知节点到锚节点之间的距离、确定未知节点的坐标.

1.1.1 确定未知节点与锚节点之间的最小跳数

已知自身位置的锚节点通过洪泛协议以其通信半径向外广播带有自身位置和跳数初始化的数据包，当邻居节点接收到锚节点的数据包之后，更新数据包中的跳数信息，也就是跳数加一，然后继续将数据包转发，同时未知节点会忽略来自同一锚节点的较大的跳数数据包，保存到锚节点最小跳数的数据包，通过此种转发方式，每个节点都得到了到网络中每个锚节点的最小跳数与最短路径[10].

1.1.2 计算未知节点到锚节点之间的距离

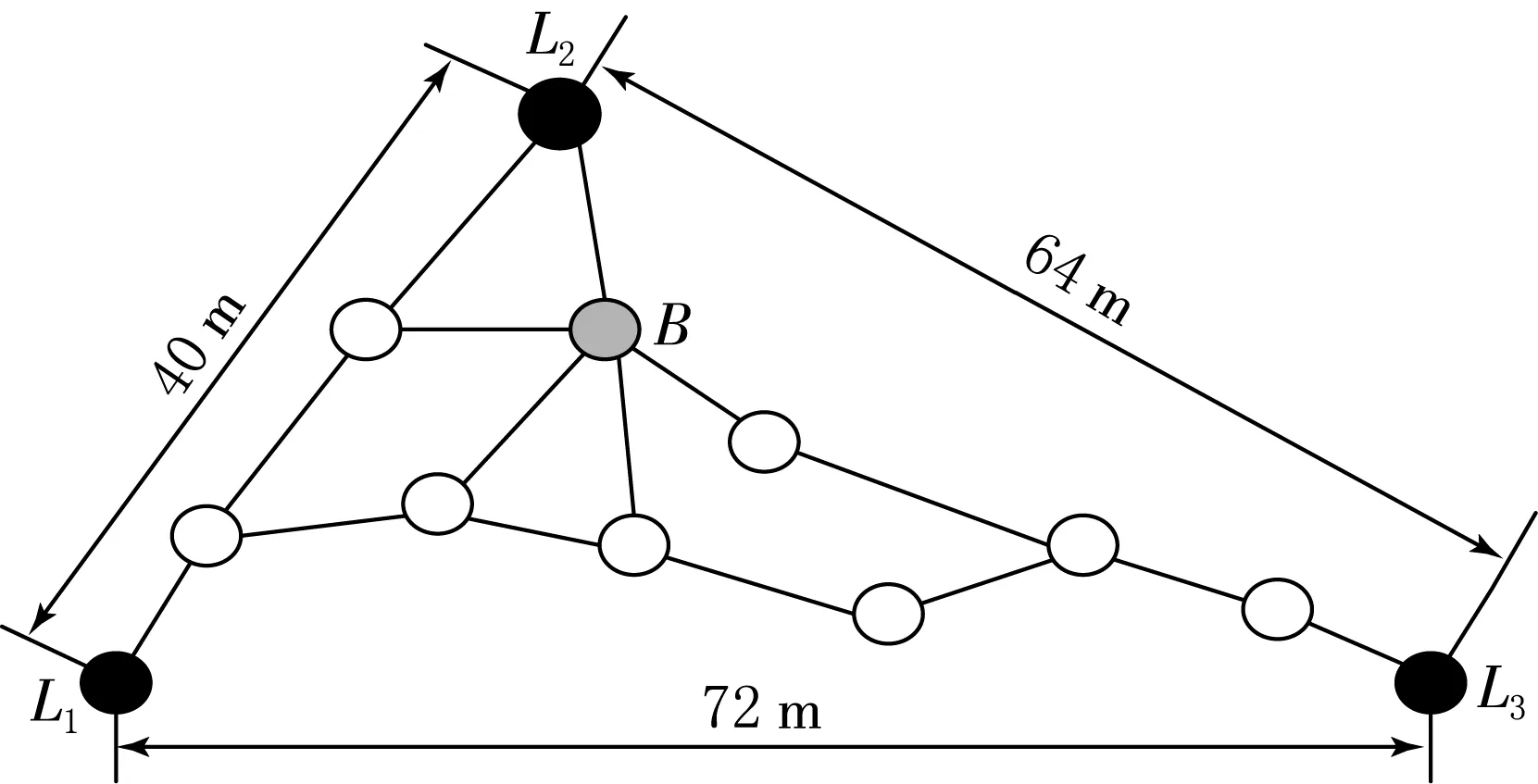
图1 DV-hop算法中节点分布示意图

传统DV-hop算法在计算距离时，主要采用距离待定位节点最近的锚节点的平均跳距作为计算到每个锚节点的平均跳距，如图1所示，离待定位节点B最近的锚节点为L2，L2的平均跳距计算过程为

(1)

此时B节点将(1)式计算出来的跳距作为自身的跳距，分别计算到3个锚节点的距离：

(2)

1.1.3 确定未知节点的坐标

利用三边测距法或者是最大似然估计法来计算未知节点的坐标.三边测量法是节点定位中计算未知节点坐标常用的方法[11]，假设未知节点的坐标是(x，y)，已知3个锚节点的坐标分别为(x1，y1)，(x2，y2)，(x3，y3)，具体的计算过程为

(3)

将上面3个式子展开之后，用第3个式子分别与上述3个式子相减，可以将(3)式转化为如(4)式矩阵相乘的形式，将3个式子中的距离记为d1，d2，d3未知节点的坐标，通过对矩阵运算获得

AX=B；

(4)

(5)

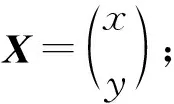
(6)

(7)

然后通过计算该坐标矩阵即可获得未知节点的坐标.

在实际的无线传感器网络中，锚节点与未知节点是随机分布的，可能参与到未知节点坐标计算的锚节点个数为n(n≥3)个，此时采用最大似然估计法来计算未知节点的坐标误差更小，最大似然估计法的计算过程与上述过程相同，区别是参与到未知节点定位的锚节点的个数不同导致的方程个数不同，其次在最后使用最小二乘法来计算未知节点的坐标为

X=(ATA)-1ATB.

(8)

1.2 传统DV-hop算法误差分析

DV-hop算法用平均跳距乘以到锚节点最小跳数的乘积来近似表示未知节点到锚节点的距离[12]，所以在后续计算过程中计算出来的坐标值也是不准确的.首先在该算法中，跳数不合理是一个重要原因，假设锚节点通信半径为50 m，在广播阶段，与之相距直线距离为5和40 m的节点都在其通信半径范围内，所以将两者的跳数都记为1跳，这是不合理的，在后续的计算过程中会进一步加大误差；同时，未知节点在计算与相邻锚节点的距离时，通常采用离未知节点最近的锚节点的跳距，没有考虑到全局网络以及锚节点的分布情况，这样就会忽略其他锚节点的跳距，在计算距离时会增大定位的不确定性；最后，在计算节点位置时，通常采用最小二乘法，普通的最小二乘法认为每项误差对总体回归直线的偏离程度全部相同，等价于权值都赋为1，各方程可信度相同.然而由于模型中误差项存在异方差性，每项误差对总体回归直线的偏离程度不同，此时普通最小二乘法无法确定各锚节点参与定位的可信度，得到的估计值不满足最优估计[13].

2 传统DV-hop定位算法改进

2.1 节点之间跳数的改进

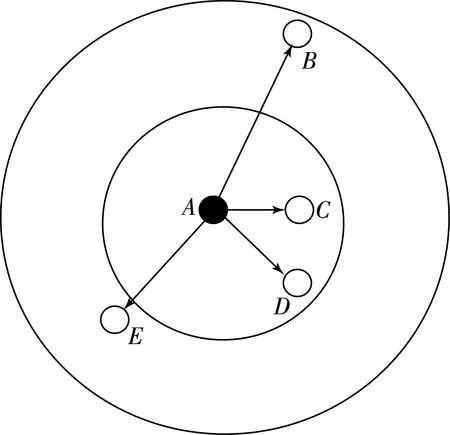
图2 锚节点广播示意图

锚节点A以通信半径R进行洪泛见图2，由图2可知，未知节点C和未知节点B都在锚节点A的通信半径内，所以两者皆可以接收到来自A的信息，此时C点和B点接收到含有位置信息和跳数信息的初始化数据包之后，此时分别将跳数加1，但是，B点和C点到A点的直线距离不同，所以两者的跳数应该不同.

具体步骤是通过设置锚节点的能量消耗模型，针对不同的发射距离D，选择不同的发射功率，定义如下的能量消耗模型，其中发送和接收m的数据需要消耗的能量公式为

(9)

通过上述过程，使得锚节点与相邻节点之间的跳数值更加接近真实跳数，将改进的跳数值加入到跳距运算的过程中，会进一步减少跳数不精确带来的定位误差.

2.2 跳距的改进

针对传统DV-hop定位算法在选择跳距时考虑片面的问题，本文首先采用改进的跳数来计算跳距，然后得到参与未知节点定位的锚节点的跳距.

如图1所示，L1，L2，L33个锚节点分别通过改进的跳数来计算跳距，假设3个锚节点得到的跳距改进值分别为Di，Dj，Dk，此时定义3个锚节点的平均每跳距离误差为

(10)

其中：w1为平均每跳误差因子；hopij，hopik，hopjk为两两锚节点之间的跳数.3个锚节点新的跳距为

(11)

假设参与未知节点定位的锚节点的个数为n个，定义平均每跳误差因子为

(12)

节点i和节点j是n个锚节点中任意的两个锚节点，且i和j是n个锚节点之中任意的两个锚节点，n个锚节点的新跳距为

(13)

考虑到锚节点距离未知节点的远近以及误差水平，距离远的锚节点所带来的误差不一定大，而距离未知节点较近的锚节点所带来的误差不一定小，所以未知节点在选择跳距时，应充分考虑误差以及距离所带来的影响，首先考虑距离带来的影响，定义锚节点i的权重系数为

(14)

式中：hopui表示待定位节点与锚节点i的跳数；hopuj表示待定位节点与锚节点j的跳数；n表示参与到未知节点定位的所有锚节点.

考虑误差所带来的影响，理想的情况应该是误差大的锚节点在未知节点的定位过程中参与度低，而误差小的锚节点参与度高[15]，定义误差因子为：

(15)

(16)

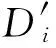
(17)

定义误差参与度因子

(18)

(18)式说明，误差较大的锚节点在未知节点位置定位的过程中参与度越低，将误差参与度因子归一化处理[16]，综合误差参与度因子以及跳数权重，分别将两者的影响因子设置为0.5，则新的跳距为

(19)

2.3 未知节点的定位

虽然对未知节点与锚节点之间跳数和跳距进行修正，但是未知节点与待定位锚节点之间的距离较真实值仍然会存在误差，所以在使用最小二乘法迭代求解时，仍然会产生迭代误差，在改进的最小二乘法中，引入加权系数矩阵，采用不同的加权系数矩阵进行定位[17].已知参与未知节点定位的锚节点的坐标为(x1，y1)，(x2，y2)，(x3，y3)，…，(xn，yn)，未知节点的坐标为(x，y).根据改进的跳数和改进跳距计算得到未知节点到每个锚节点的距离分别为d1，d2，d3，…，dn，可得

(20)

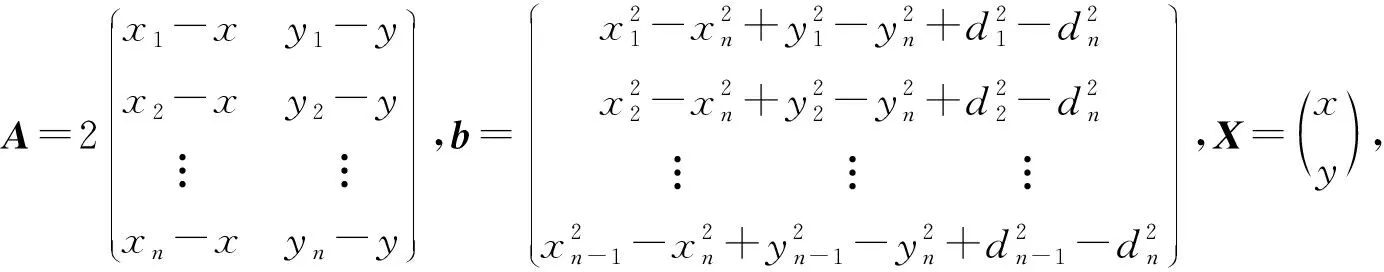
(21)

3 仿真结果与分析

仿真采用MATLAB2016a将节点随机分布在100 m×100 m的正方形区域内，观察锚节点的比例、节点的总数量、节点的通信半径对于平均节点定位误差的影响.图3是节点随机分布示意图，图3中设置100个节点，20个锚节点，星号代表锚节点，圆点代表未知节点.

本文选用相对定位误差作为衡量节点定位的效果，公式为

(22)

式中：N代表节点的总数，B代表锚节点的数量，R代表节点的通信半径，(x，y)是节点位置的真实值，(xi，yi)是节点位置的估计值.

图4是DV-hop算法中每个节点的定位误差，由图4可以看到节点的误差分布不均匀，这和节点的分布位置有关，节点分布均匀，误差的总体水平会下降，节点分布不均匀，误差的总体水平较高.

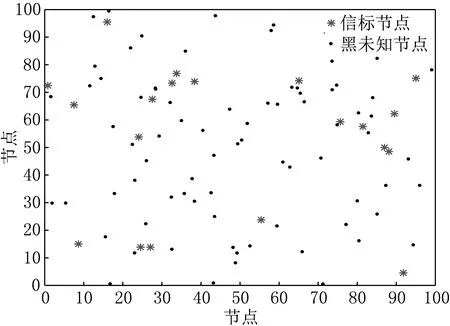
图3 节点随机分布示意图

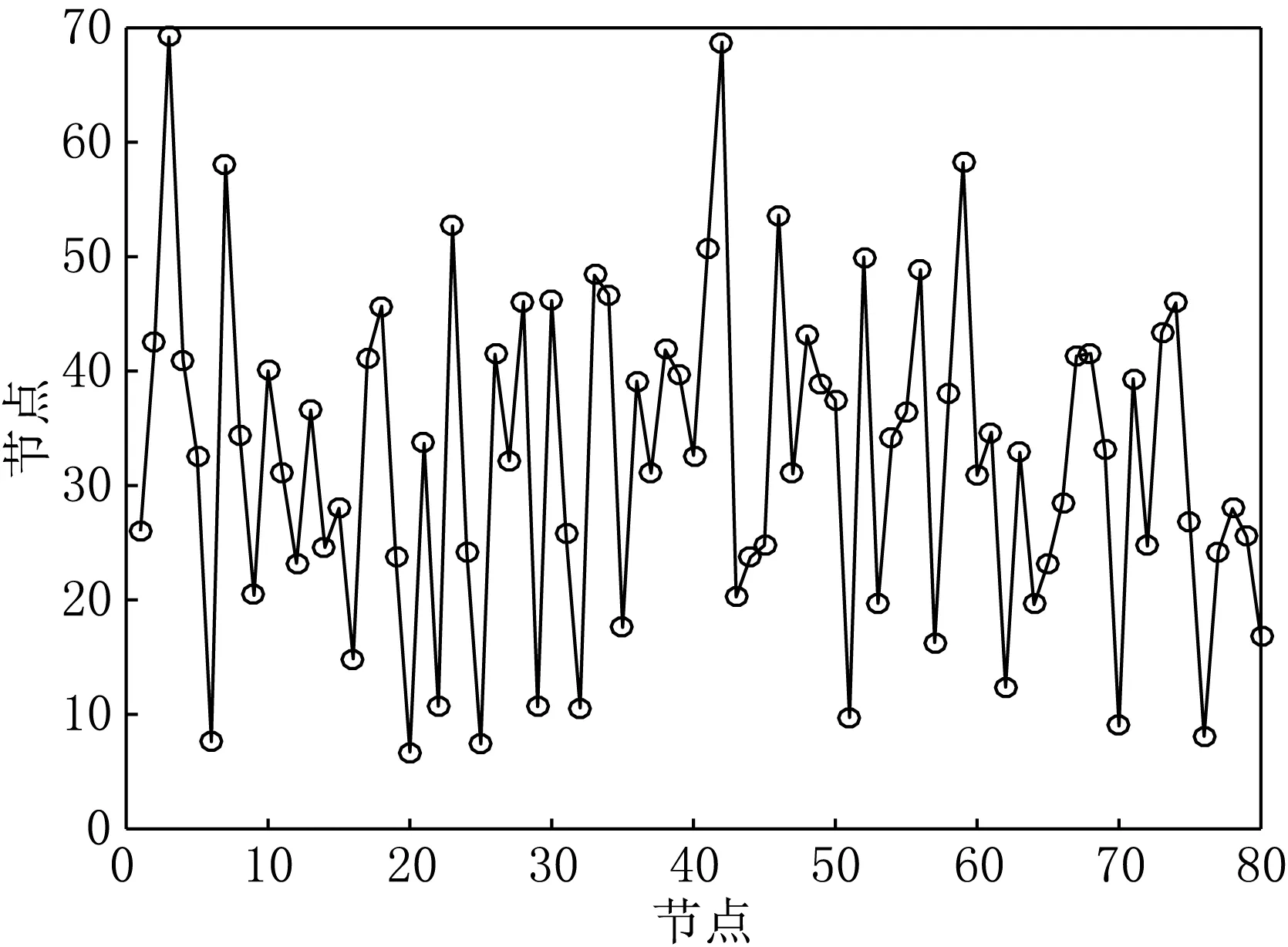
图4 每个节点绝对误差分布示意图

为了对改进的算法进行评估，在相同的网络环境下，每改变一次变量对实验模拟10次，取平均值作为最后的结果，将通信半径、锚节点的比例以及节点的数量作为3个变量对本文改进的算法、DDV-hop算法以及原算法进行仿真，比较三者之间的定位精度.

(1) 节点总数相同，锚节点的比例相同，通信半径不同.

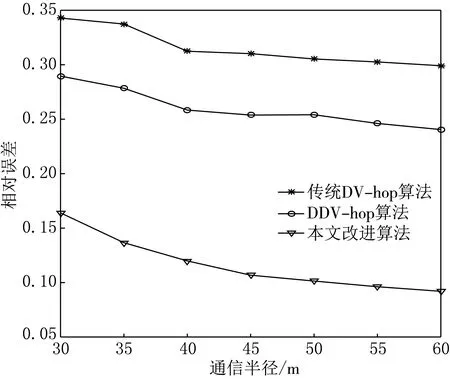
图5 算法随通信半径改变的误差比较

图5是各个算法随节点的通信半径的改变定位误差而改变的效果仿真图，节点的总数相同，锚节点的比例相同，通信半径分别从30 m取到60 m.从图5中可以看出，随着通信半径的增加，算法的误差逐渐减小.从仿真结果来看，本文改进算法相对于传统的DV-hop算法和DDV-hop算法更优，定位精度更高，误差更小.

(2) 节点总数相同，通信半径相同，锚节点的比例不同.

锚节点的比例是影响算法稳定度的一个重要原因(见图6)，随着锚节点比例的增加，本文改进算法的定位精度变化不是很明显，波动范围较小，传统的DV-hop算法的波动范围较大.同DDV-hop算法相比，本文改进算法的定位精度更高，定位精度提高了15%左右；相对于传统的DV-hop算法来说，定位精度提高了25%左右.

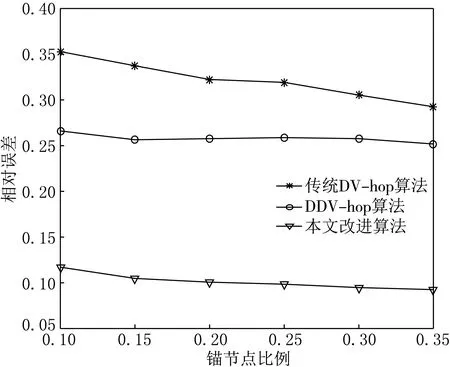
图6 算法随锚节点比例改变的误差比较

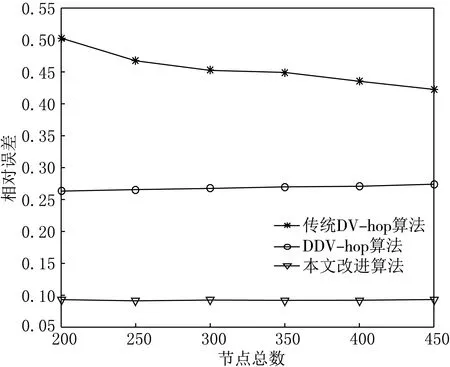
图7 算法随节点总数改变的误差比较

(3)通信半径相同，锚节点的比例相同，节点的总数不同.

节点总数的增加，会导致节点的定位精度的变化(见图7).从图7可以看出，随着节点总数的增加，定位精度相对不会升高，而是相对保持一个平稳的状态，特别是相对于本文改进算法来说，因为随着节点数的增加，需要锚节点参加定位的频率就越大，同时受到参与度因子的影响，节点的定位精度相对稳定，不会有太大的起伏变化.

4 结束语

首先对传统的DV-hop算法的原理以及工作过程进行了介绍，分析了引起DV-hop算法误差的主要原因，利用多通信半径的方法进行改进跳数，利用跳数加权以及锚节点的参与度作为考量锚节点参与未知节点定位的主要因素，进行改进跳距，同时在计算未知节点位置的过程中加入误差的协方差矩阵和加权系数矩阵来改进传统的最小二乘法，最后通过仿真实验将改进的DV-hop算法以及DDV-hop算法、传统的DV-hop算法进行比较，相对于后两者，改进算法的定位误差进一步减小，定位精度进一步提高.