基于反步滑模算法的植保无人机姿态控制研究

冯 江，张 慧，张喜海，杨 方

（东北农业大学电气与信息学院，哈尔滨 150030）

近年来，随着科技进步，植保无人机逐渐进入国内农业植物保护领域[1]，在林业防火、灾后救援、电力巡线、无人机快递投送、航拍摄影、三维建模等方面应用广泛[2]。由于植保无人机需在不同地势作业，负载较大，电机和螺旋桨需高速旋转才能正常飞行，增加其发生故障风险[3]。因此，如何在植保无人机发生故障时，保证飞行姿态稳定为无人机姿态控制研究热点问题。当无人机姿态失衡时，容错控制为保证无人机姿态平稳关键，故障信息获取为实现容错控制有效手段[4]。何志辉等通过自抗扰模糊参数优化控制策略，针对纵列式植保无人机发生故障问题，设计扩张状态观测器，采用模糊控制在线调整增益参数，并验证所提算法鲁棒性，但算法复杂增加飞行器反应时间[5]；张莉采用参数优化方法，分析植保无人机田间作业工作原理，建立二次性能指标控制模型，保证植保无人机飞控系统性能稳定，这种参数优化方法需要一定前置条件，且飞行时外界环境与飞行器模型参数实时变化[6]；张红欣等考虑植保无人机在喷洒农药时，极易受外界因素影响而改变飞行姿态，研究一种径向基函数-比例-积分-微分控制方法，将神经网络、模糊控制、PID控制技术耦合，确保飞行姿态实现自适应平衡，此模型需考虑整机作业轨迹控制等因素，对模型精准度要求较高[7]。

本文基于反步法控制和滑模法控制，结合飞行器常用IBC 算法、SMC 算法和LQR 算法姿态控制特性，运用反步滑模控制方法设计容错控制器，构造反步滑模观测器实时观测植保无人机故障状况，对四种算法分别在无故障和有加性故障干扰情况下作仿真对比，并对反步滑模算法开展试验。

1 植保人机故障模型

图1所示为植保无人机整体结构，电机1和电机2 逆时针方向转动，电机3 和电机4 顺时针方向转动。建立导航坐标系E（xe，ye，ze）、机体坐标系B（xb，yb，zb），其中（φ，θ，ψ）分别为滚转角、俯仰角和偏航角。

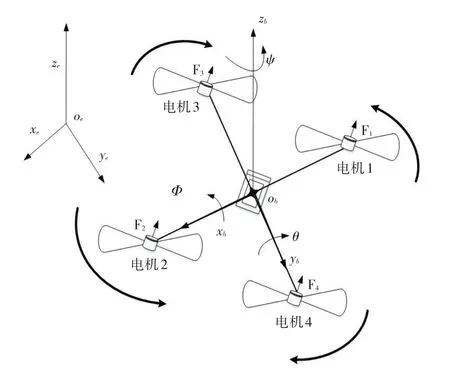
图1 植保无人机结构Fig.1 Plant protection UAV structure

建立动力模型作出假设：

①假设无人机质量为均匀分布，飞行时为刚体结构[8]；

②假设无人机重心与质心重合；

③假设无人机在行驶过程中不受地球自转、公转及地面效应影响。

从导航坐标系[9]到机体坐标系的旋转变换矩阵如式（1）所示（其中c表示cos，s表示sin）：

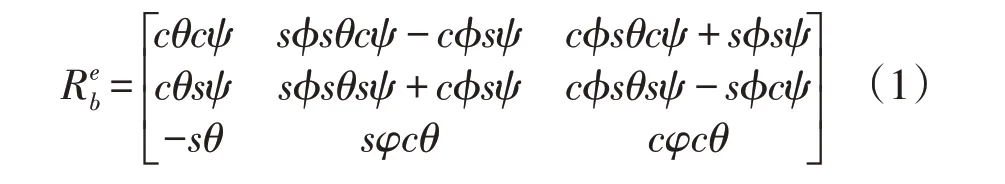
由牛顿第二定律可知：

其中，F表示4 个旋翼总升力，即F=F1+F2+F3+F4，其中，Fi=，k为升力系数，a为线加速度，m为四旋翼飞行器质量。

得到四旋翼飞行器动态模型如式（3）所示：

式（3）中，x、y、z分别为导航坐标系3个位置分量；姿态角表示为φ、θ、ψ，依次为滚转角、俯仰角和偏航角；Jr是旋翼转动惯量；Jx、Jy、Jz依次为3个轴惯性力矩；m为机身重量；g为重力加速度；l为轴距；Ω为电机在同步过程中扰动；Ωi（i=1,2,3,4）表示4 个电机转速。其中

考虑到四旋翼无人机在飞行过程中可能发生故障[10]，引起执行机构失效值近似为常数，将损失表达为各通道输入量[11]，间接表示为俯仰、横滚、偏航及高度通道输入损失，结合式（3），可将此时状态方程改写为：

在四旋翼无人机动态方程中，在式（4）基础上加入加性故障干扰，即为连续有界的一种加性故障干扰函数f（ii=1,2,3,4,5,6）。通常在容错控制时，加性故障是典型描述故障的方法，在系统动态方程中添加一个干扰性，即添加一个故障函数[12]，表示在系统中故障的影响。此外，还考虑在飞行时系统受外界环境干扰影响。因此，在四旋翼动态模型函数中依次加入干扰函数g（ii=1,2,3,4,5,6），建立如式（5）所示四旋翼故障模型：

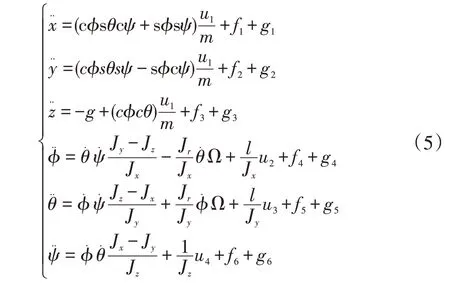
2 控制器设计

2.1 状态观测器简化模型

电机、电调、螺旋桨失灵或未知环境因素干扰的不确定使执行机构发生加性故障，引发系统执行机构失效值近似为常数，将这种失效值间接转为姿态角通道及高度通道的控制输入损失[13]。其中（xd，yd，zd）和（x，y，z）依次分别为无人机位置的期望值和实际值，（φd，θd，ψd）和（φ，θ，ψ）依次为无人机姿态的期望值和实际值，（U1，U2，U3，U4）为控制观测系统控制量。首先对系统故障模型作简化处理，令系统控制输入量为：

状态变量为：

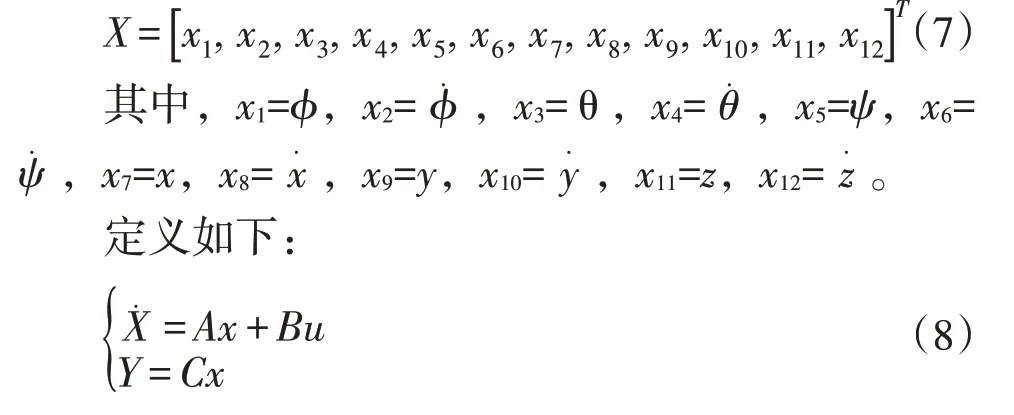
x为状态变量，Y为输出变量，u为输入变量。

则四旋翼无人机模型简化后，带有加性故障的执行器状态空间矩阵如下：

式（9）中，a1=（Jy-Jz）/Jx，a2=（Jz-Jx）/Jy，a3=（Jx-Jy）/Jz，b1=l/Jx，b2=l/Jy，b3=1/Jz。

2.2 线性二次型调节器

线性二次型调节器在先行动态环节计算量小、硬件实现容易。通过构造中间控制量，四旋翼系统可由线性动态和非线性静态两个环节组成[14]，对线性动态环节设计线性二次型调节器[15-16]，并设计LQR。解算非线性静态环节，分配到实际系统中控制输入通道。

将式（8）离散化，得如式（10）所示离散系统：

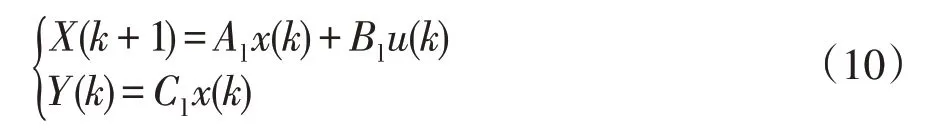
其中，Al，Bl和Cl分别为离散时间的状态、输入和输出矩阵。“k”表示离散时间步长，k取整数。

LQR 的最优控制时求反馈控制律[17]，令u=-kx，在区间[t,∞]中系统从非平衡状态到零点附近。其性能指标为：

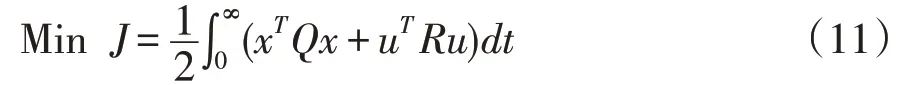
其中，Q和R分别为半正定与正定实对称常数矩阵，且Q为状态变量加权矩阵，R为控制变量加权矩阵。性能指标取极小值，根据Hamilton方程有：

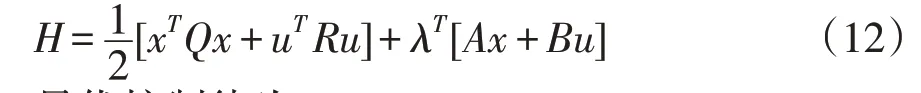
最优控制律为：

可得：

其中λ=Px。

本文使用Matlab 利用LQR（A,B,Q,R）函数直接对反馈系数求解，并验证LQR（A,B,Q,R）函数系统性能。

2.3 反步法控制器设计

反步法控制被广泛用于非线性系统，核心思想是将复杂系统划分为多个子系统，且子系统数量不大于整个系统阶数，减少计算时间[18]。每个子系统通过中间虚拟量或Lyapunov 函数作递归构造，解决非线性因素的不确定性影响[19]。

以滚动通道为例，建立系统动态方程：

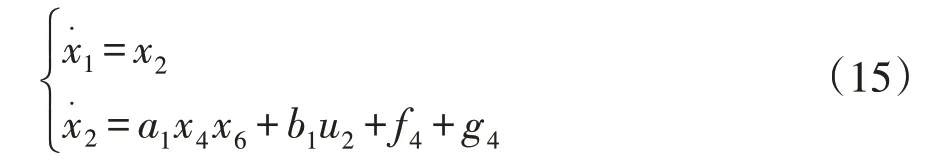
式（15）中，f4表示一个有界故障，g4作为一个常数，表示外界干扰，为限定条件，ρ3为外界干扰变化量上界。

状态观测器模型可简化为：

步骤一：取选定的Lyapunov函数V1：

根据Lyapunov 稳定理论分析可得，由于V.

1 ＜0，为此增加其虚拟控制量，使其作为e1子系统的虚拟控制，另（c1＞0为可调参数），则x2误差e2为：

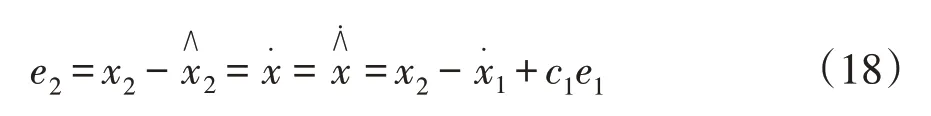
对式（17）求导并结合式（18）可得：

步骤二：构造增广Lyapunov函数V2：

式（20）中，ef=f4-ε4，其中f4表示已知滚转角通道执行器加性故障值，但f4值无法实际测量，在此使用ε4为估计值，定义积分项如下式：

对式（20）求导易知V.2＜0，说明步骤二设计中系统渐近收敛，则：

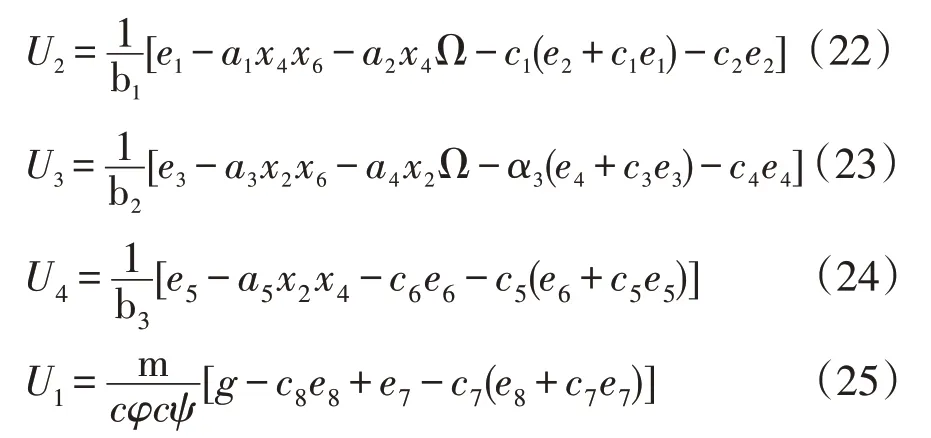
2.4 滑模控制器设计

基于反步法设计的控制器仍有不足，其被控对象要建立精准的数学模型。与反步法控制相比，滑模控制物理简单且控制性能优良。运动轨线被强迫为滑动流行状态，并保持一段时间。滑模变结构控制与常规控制相比具有不连续控制特点，这种方式促使系统按照既定轨迹作高频率、小幅度震荡运动，为“滑模”运动[20]。滑模运动的滑动模态可认为设计与外部环境参数变化及系统内部环境变化无关，具有良好鲁棒性。如果将反步法控制与滑模法控制结合，则可增大控制系统使用范围，对于控制律设计的鲁棒性较好。本文依据滑模变结构原理，采用指数趋近控制律改变趋近运动的动态特性。具体设计如下：

与反步法控制一致，以滚转通道为例，系统动态方程为：

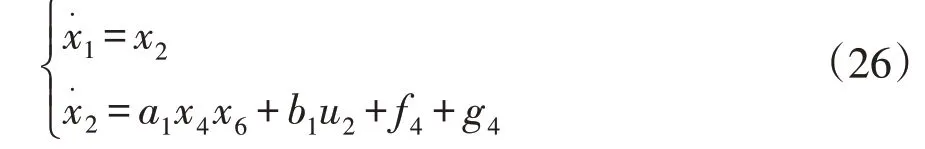
取滑模趋近率为：

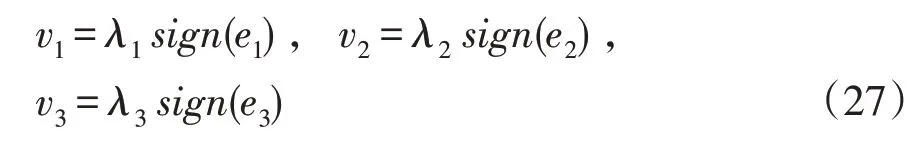
滑模控制易出现抖动，将sgn（s）函数改为sat（s）饱和函数可减少系统运行过程中抖动。

对应切换面为：

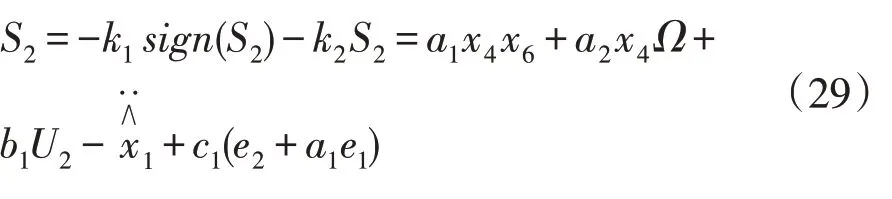
2.5 反步滑模控制器设计

由于四旋翼具有欠驱动、强耦合控制特点，根据式（4）表示的故障模型方程设计容错控制器总体容错控制算法如图2 所示，控制结构包括位置控制和姿态控制，其中姿态控制期望的偏航角ψd被设定为已知，而期望的俯仰角φd、滚转角θd需经位置控制得到；通过姿态控制得到的通道控制量U2、U3、U4和高度通道控制量U1分配给执行机构控制输入，完成四旋翼无人机控制。对于容错控制器设计分两步。首先通过滑动控制方法构建滑模观测器，有利于系统稳定性分析；其次结合反步法控制，研究执行器故障时容错控制器的设计。

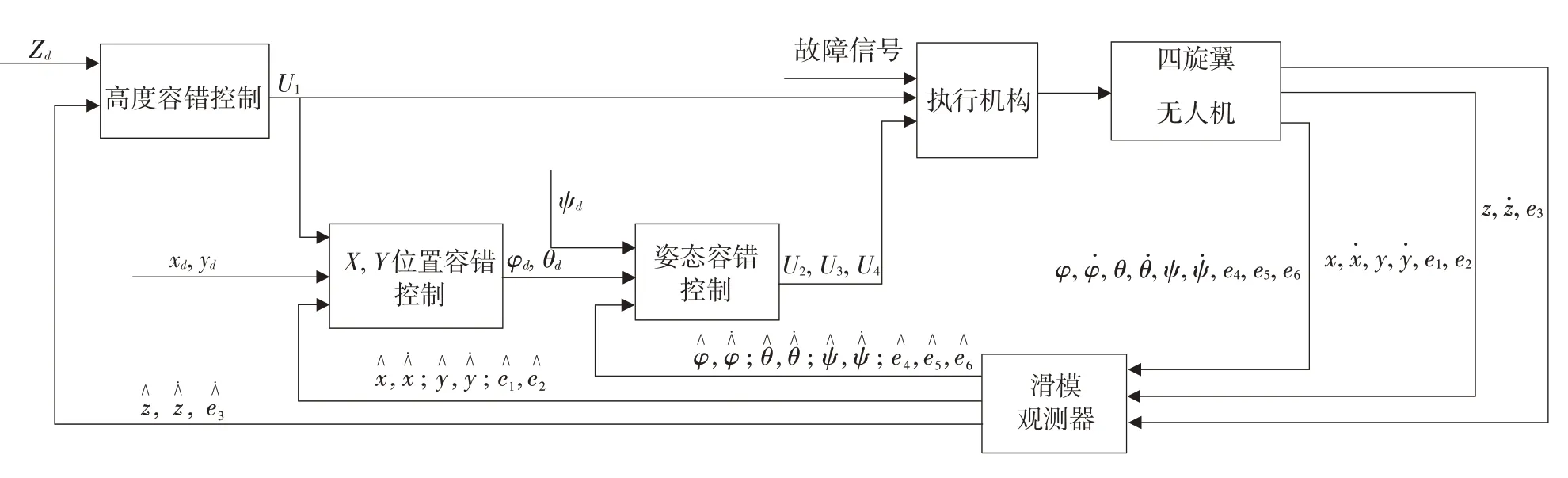
图2 容错控制结构Fig.2 Fault-tolerant control structure

参照上述反步法控制器设计与滑模法控制器设计，则反步滑模控制算法输入控制为：

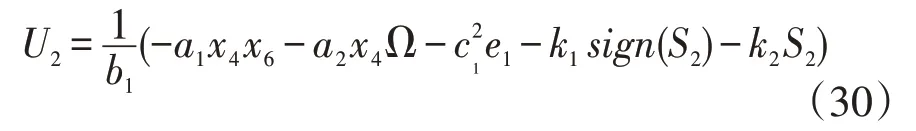
因此，其他通道电机输入控制为：

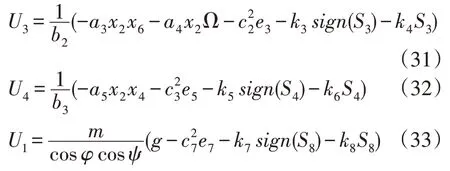
3 仿真验证与物理试验

在Matlab/Simulink环境下对所设计的控制算法分别在无故障干扰和有加性故障干扰情况下开展仿真验证。假使四旋翼无人机初始姿态为[0°0°0°]，期望姿态为[80°40°60°]，表1为四旋翼参数。

表1 植保无人机模型参数Table 1 Plant protection UAV model parameter

3.1 无干扰仿真试验

首先，根据以上模型建立，设计相关仿真。表1所示为仿真参数。根据线性二次型算法中，通过多次试凑得到控制器Q和R分别为：

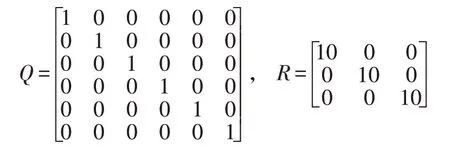
得出状态反馈矩阵为：

在无故障干扰条件下，仿真3 种结果如图3～5所示。

基于搭建的四旋翼无人机模型，图3为4种控制算法下四旋翼无人机姿态响应曲线，图4为4种控制算法下四旋翼无人机飞行速率仿真曲线，图5是4 种控制算法下四旋翼无人机电机速率仿真曲线。图3、4 响应曲线分别给出四旋翼横滚、俯仰和偏航3 个方向响应状态，图5 给出4 个电机响应情况，得出以下分析结果。

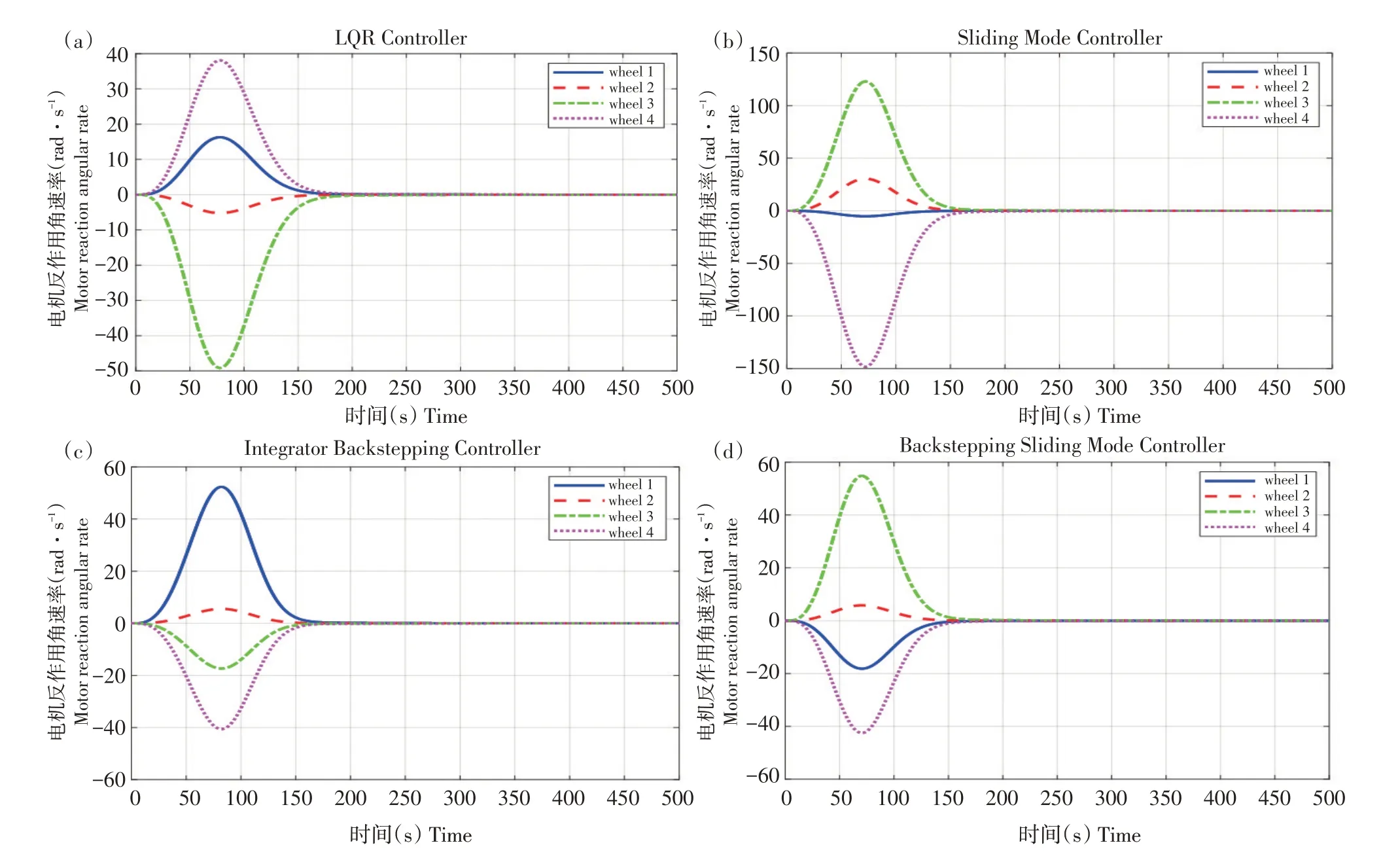
图5 LQR、SMC、IBC、BSC算法无干扰电机速率仿真结果Fig.5 LQR,SMC,IBC,BSC algorithm interference-free motor speed simulation results

由图3可知，对于四旋翼系统，在受到相同系统输入时，3种方法均可在一段时间趋于稳定，具有良好控制效果。图3a 中LQR 滚转角收敛时间为200 s，图3b中SMC滚转角收敛时间为200 s，图3c中IBC滚转角收敛时间为200 s。3个控制算法稳定时间一致，均可在短时间达到快速稳定状态。通过仿真曲线可知在趋于稳定过程中，LQR和IBC响应均未出现振荡，SMC算法有较小抖动。

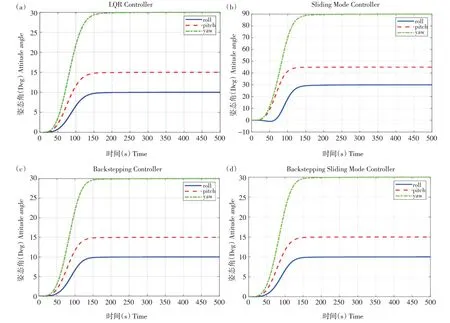
图3 LQR、SMC、IBC、BSC算法无干扰姿态仿真结果Fig.3 LQR,SMC,IBC,BSC algorithm interference-free attitude simulation results

图4 中四旋翼飞行速率响应曲线均在200 s 时趋于0，响应时间及各通道最大响应角速度见表2，SMC算法最先到达最大角速度，以滚转角为例，最大响应为1.121 deg·s-1。IBC算法在82 s时角速度达到峰值，滚转角角速度峰值为0.08583 deg·s-1。

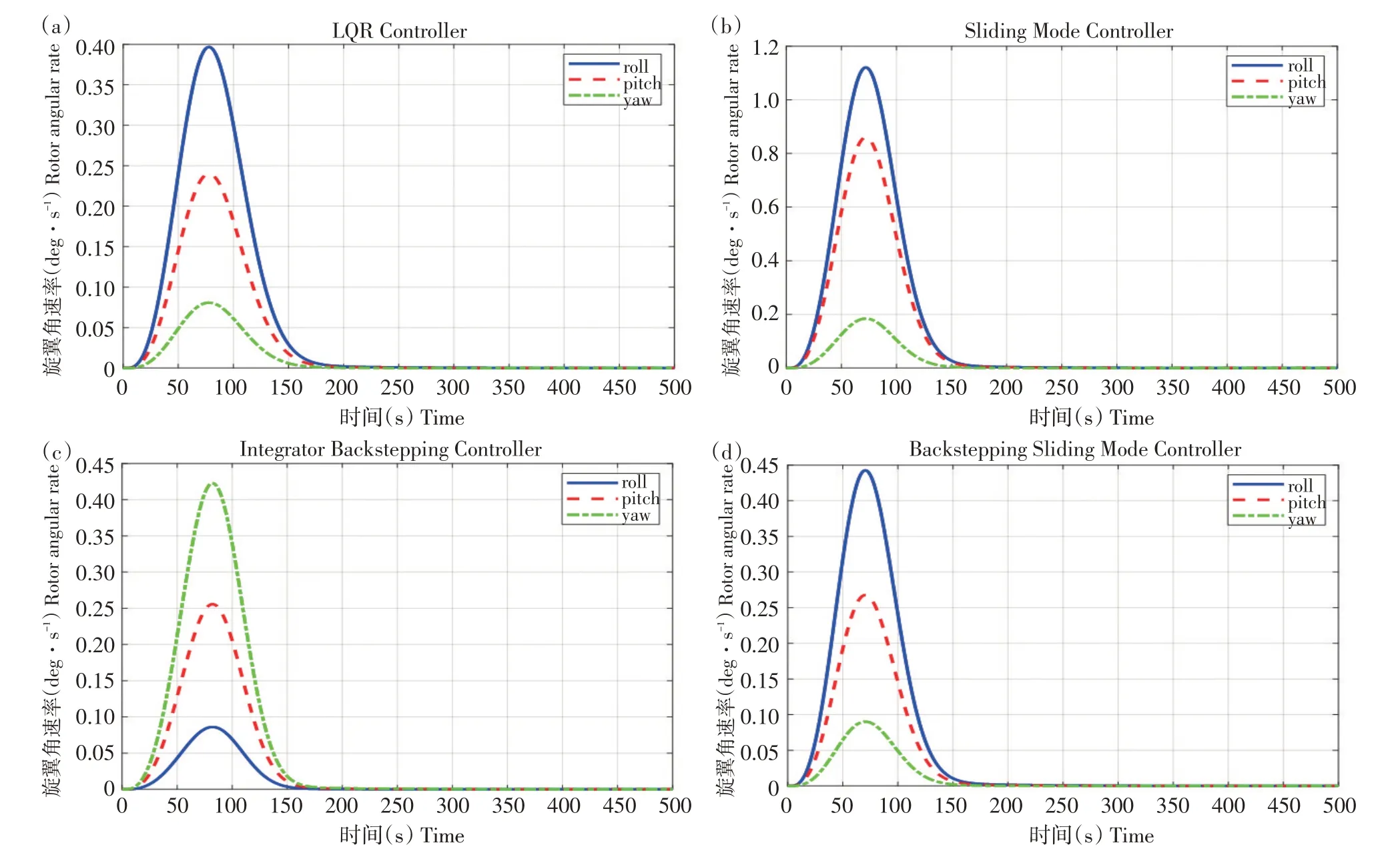
图4 LQR、SMC、IBC、BSC算法无干扰飞行速率仿真结果Fig.4 LQR,SMC,IBC,BSC algorithm interference-free flight rate simulation results

图5表示四旋翼每个电机角速度响应曲线，每种算法电机最大响应值如表3 所示，3 种算法电机转速在78、72、82 s处达到响应峰值，这3个时间点分别对应表2中姿态响应时间，此时达到四旋翼最大响应峰值，电机转速变化较大，以求快速跟上期望轨迹。

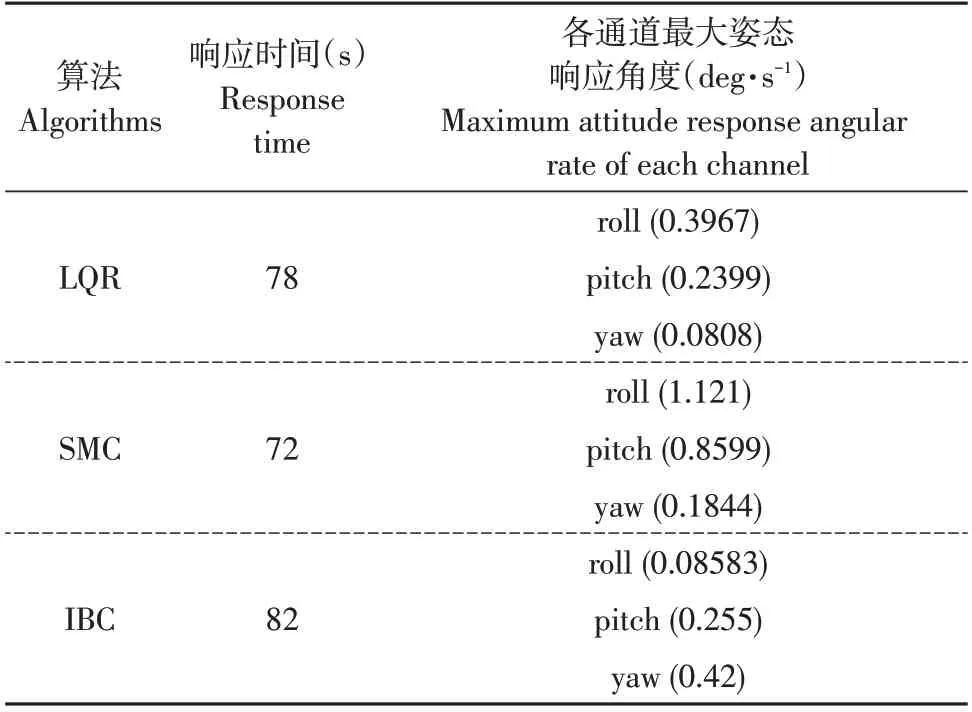
表2 3种算法姿态响应峰值参数Table 2 Three algorithms attitude response peak paremeter

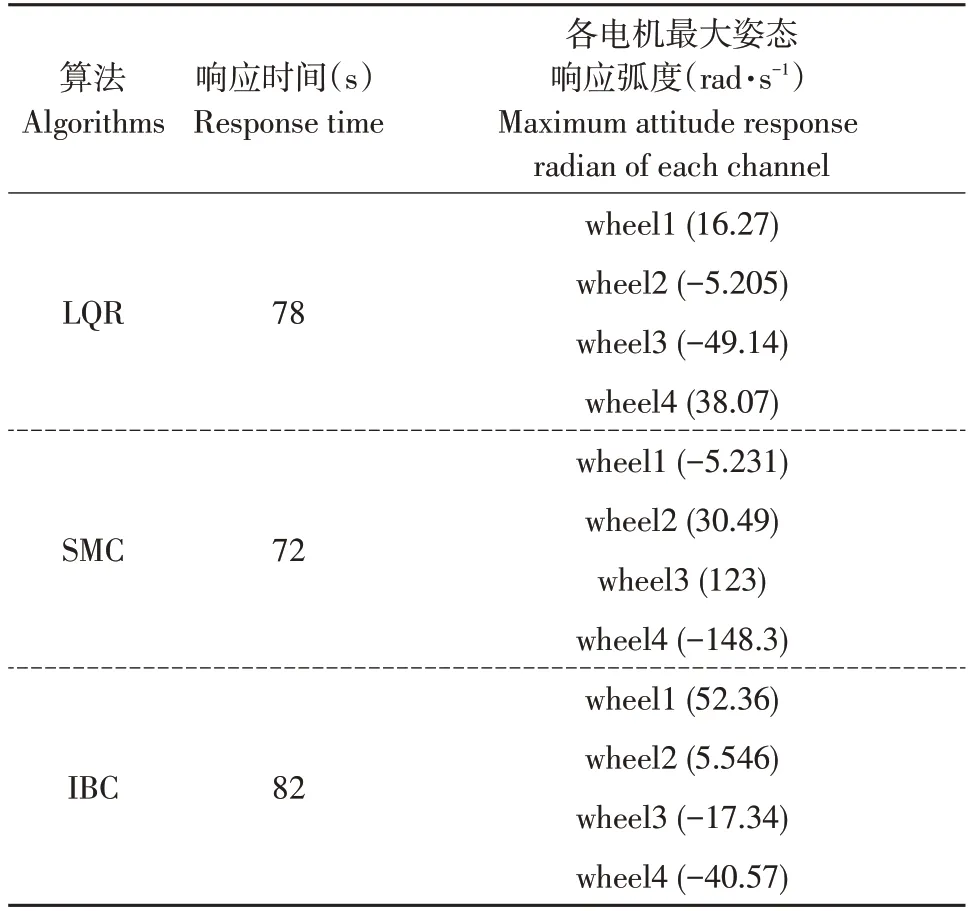
表3 3种算法电机姿态响应峰值参数Table 3 Three algorithms motor attitude response peak paremeter

3.2 有界干扰仿真试验

在实际飞行环境中，四旋翼无人机除系统本身出现故障，还会遇到外界干扰，如外界阵风等。在仿真模型中，于150 s 时加入阶跃响应，验证算法有效性。图6～8为仿真结果，由此得到分析结果：

①由图6～8 可知，在阶跃响应信号干扰下，四旋翼无人机姿态响应、飞行速率、电机反作用力均受到一定程度影响，图6～图8a 中LQR 干扰试验四旋翼姿态响应未收敛于平衡状态；

②从图6～图8b 中，SMC 算法在150 s 时加入干扰，系统几乎未受影响，可快速恢复到平衡状态，鲁棒性较好，但滚转角在开始时有较小抖动；

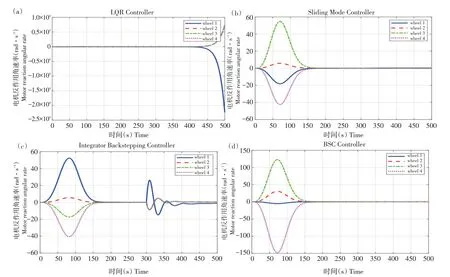
图8 LQR、SMC、IBC、BSC算法干扰下电机速率仿真结果Fig.8 Motor speed simulation results under the interference of LQR,SMC,IBC,and BSC algorithms

③同理，IBC 试验在150 s 时加入干扰，系统姿态角变化较小，俯仰角、滚转角、偏航角所受干扰影响较小，姿态响应产生较小抖动，电机响应在150 s后产生抖动，在100 s内趋于稳定，调节时间短，偏差小，鲁棒性较好。

3.3 反步滑模算法验证与物理试验

基于以上3种算法试验结果可得知，在无外界干扰情况下，3种算法均可快速达到平衡状态；在加入外界干扰条件下，3 种算法均产生一定偏差，将反步法控制与滑模法控制方法结合，在Matlab/Simulink 下验证反步滑模控制系统，结果如图3～8所示。

由图3～5可知，在无干扰仿真环境下，反步滑模法可达到快速平稳状态，达到期望的姿态角；由图6～8 可知，同样在300 s 时加入阶跃响应故障干扰信号，姿态角几乎未受影响，无抖动和超调量，电机反作用姿态曲线较平稳，可知，反步滑模控制具有及时响应特性与良好鲁棒性，有较强容错控制能力。

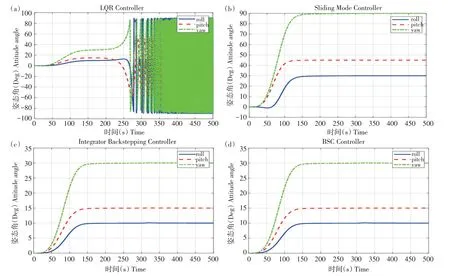
图6 LQR、SMC、IBC、BSC算法干扰下姿态仿真结果Fig.6 Attitude simulation results under the interference of LQR,SMC,IBC,and BSC algorithms

图9为将反步滑模算法写入飞行控制器开展现场试飞试验，在反步滑模控制系统下，植保无人机平稳飞行，在加性故障环境下无人机受到影响较小，鲁棒性较好。

图9 BSC飞行试验Fig.9 BSC flight test

通过Pixhawk飞行控制器MPU6050模块可获得飞行角速度和角速度数据，下图是飞行过程中姿态曲线图。从图10中曲线1与曲线2可知，两条线重合度较高，滚转角目标值与实际值接近，验证BSC算法性能较高，使得植保无人机很快达到预期角度。图11为飞行控制器IMU姿态信息，由曲线3数值与曲线4 数值可知，AccX、AccY 两个轴的姿态误差尽在±2 m·s-2，飞行控制较稳定，震动不明显，BSC算法有良好的鲁棒性。

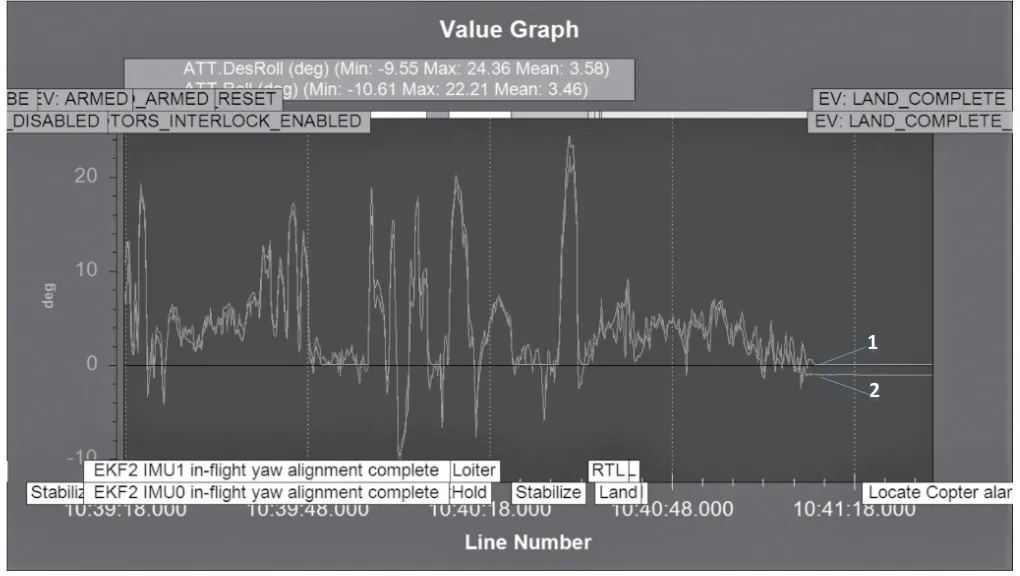
图10 BSC飞行姿态跟踪曲线图Fig.10 BSC flight attitude tracking curve

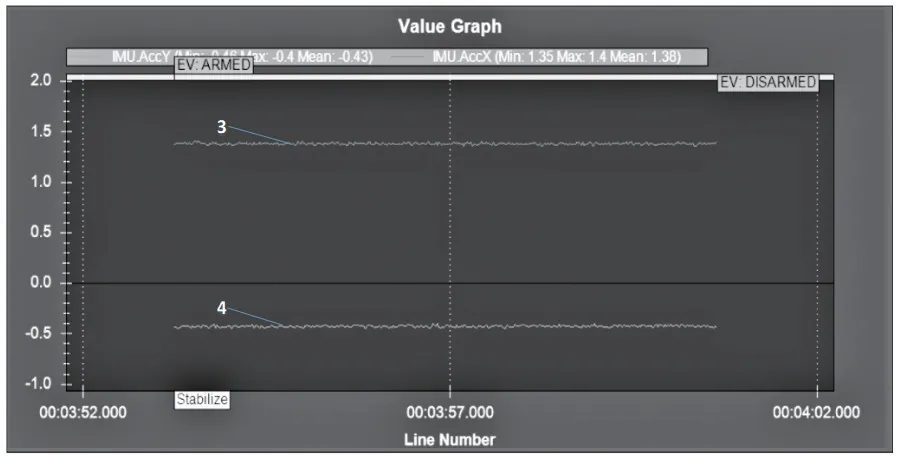
图11 BSC飞行试验IMU误差Fig.11 BSC flight test IMU error

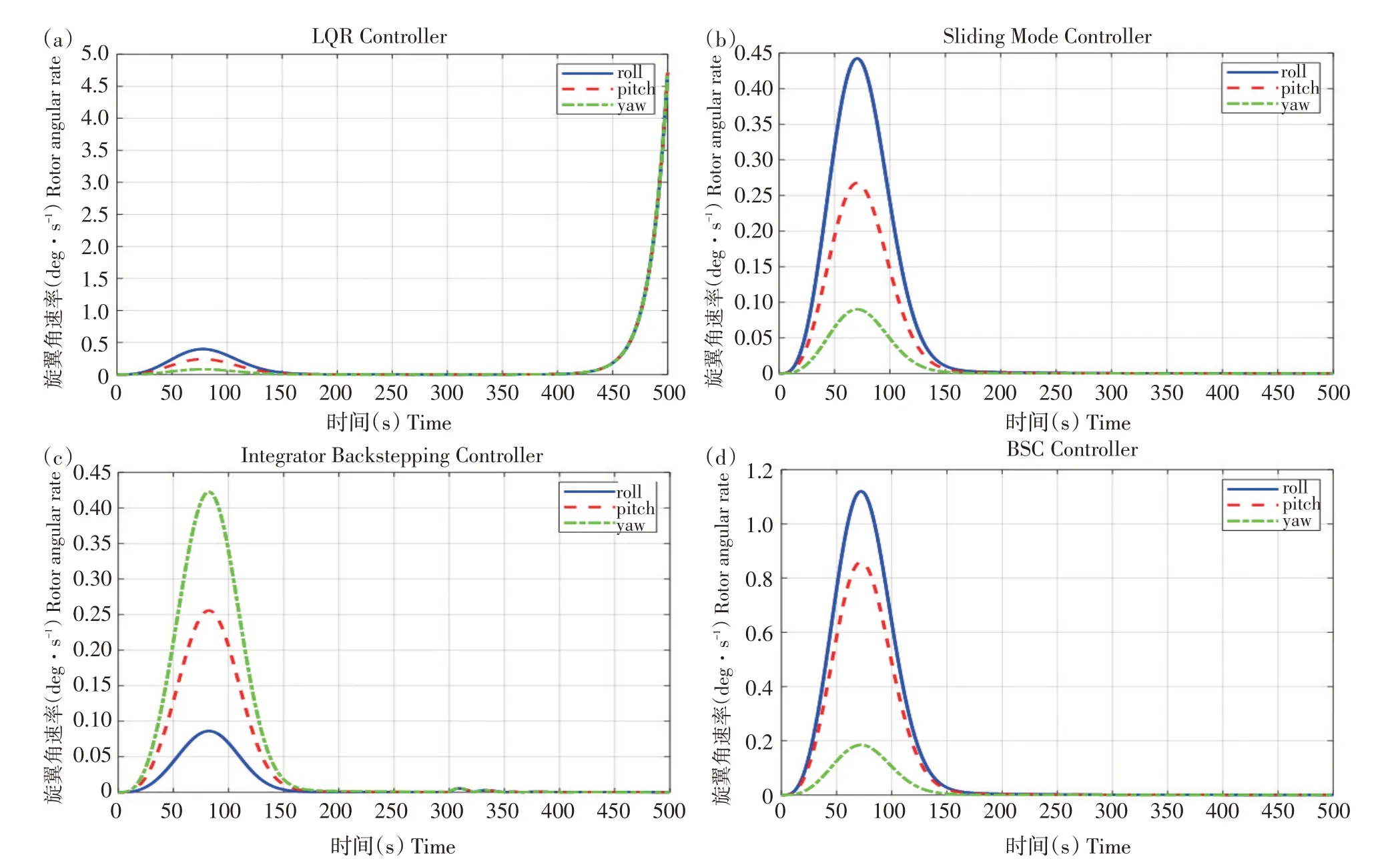
图7 LQR、SMC、IBC、BSC算法干扰下飞行速率仿真结果Fig.7 Flight rate simulation results under the interference of LQR,SMC,IBC,and BSC algorithms

4 结论

针对植保无人机系统模型不确定或存在外界环境干扰情况下，导致作业时植保效率低下问题，对常用的3种控制算法开展仿真试验。

分析中得知，LQR 控制算法在受到加性故障干扰后飞行器姿态无法保证快速恢复到平衡稳定状态；SMC 算法当滑动的轨迹到达滑模面后，易产生抖动；BSC算法在设计控制律的过程中对系统反馈性能要求较严格，算法复杂。

通过将反步法控制与滑模法控制结合，并验证IBC算法有效性。从仿真实验分析得知，反步滑模算法结合反步法控制与滑模法控制的性能，可以全局优化系统参数，并自适应调整加权矩阵，在加入外界干扰的条件下电机的姿态较为稳定，并能快速趋于稳定状态；从植保无人机现场的飞行情况可知，植保无人机使用反步法模算法，姿态的轨迹跟踪性好，响应及时，遇到外界风力干扰时容错控制性强，鲁棒性良好，保证植保无人机能够有效作业，提高无人机植保的工作效率。