基于SLR数据的雷达探测精度分析方法

罗震龙， 宋嘉政， 褚福勇， 代 林， 张小各 ， 杨 超， 杨生忠

(1. 中国人民解放军63786部队， 新疆乌鲁木齐 830000；2. 中国人民解放军32035部队， 陕西西安 710000)

0 引 言

随着信息化战争对空间技术的依赖性不断增强，空间目标监视技术已经成为各航天大国竞相发展的空间技术“制高点”[1]。空间目标监视雷达凭借其全天时、全天候的技术优势，已成为空间目标监视体系内的骨干设备，其主要作用是对太空中的导弹、卫星、空间碎片、空间站、宇宙飞船和天然陨石等空间目标进行探测和跟踪，实时掌握空间目标的运动态势[2]。空间目标监视雷达的主要功能是发现空间目标并对空间目标定位，雷达的探测精度直接影响到空间目标的定轨精度，决定了掌控太空态势的准确性。因此，分析雷达探测精度对于空间目标监视有着重要意义。

要分析雷达的探测精度，首先要知道被测目标的准确位置。目前，卫星激光测距(Satellite Laser Ranging，SLR)是卫星观测中测量精度最高的技术手段[3-4]，其通过精确测量激光信号从地面站到卫星的往返飞行时间获得星地间精密距离，单次测量精度已提高到亚厘米级，目前正向毫米级发展[5-6]。SLR的定位精度远高于以微波为探测手段的雷达，因此可将其测量数据作为参考对雷达探测精度进行分析。但SLR精密星历数据多是以5 min或15 min为间隔的空间目标三维坐标，空间目标监视雷达探测的是以1 s或更短时间间隔的探测数据，因此想要得到探测时刻空间目标的参考位置就需要对SLR数据进行插值处理[7-8]。本文首先对比了不同插值算法的插值效果，而后介绍了SLR数据与雷达观测数据的坐标转换方式，最后将效果最优的插值结果作为参考值对雷达探测精度进行分析。

1 插值算法分析

1.1 拉格朗日插值法

已知有给定的k+1个采样节点数据(t0,x0),(t1,x1),…,(tk,xk)，其中tj对应采样节点的时刻，xj对应节点时刻目标的位置，则根据插值节点得到的拉格朗日插值多项式[9]为

(1)

式中，

拉格朗日插值系数lj(x)的特点是在xj上的取值为1，在其余点xi,i≠j上取值为0。通过给定k+1个互异的插值节点，求得一条n阶多项式代数曲线近似表示待插值的函数曲线，从而获取所需观测时刻的目标近似坐标。

1.2 实例分析

本文采用由Space Geodesy Facility(SGF)提供的日本AJISAI测地卫星的SLR数据进行插值实验，数据的采样时间为2020年6月30日0时0分0秒至7月2日23时56分0秒，采样间隔为4 min，数据样本提供采样时刻及卫星在X,Y,Z三个方向上的坐标，数据内容如表 1所示。

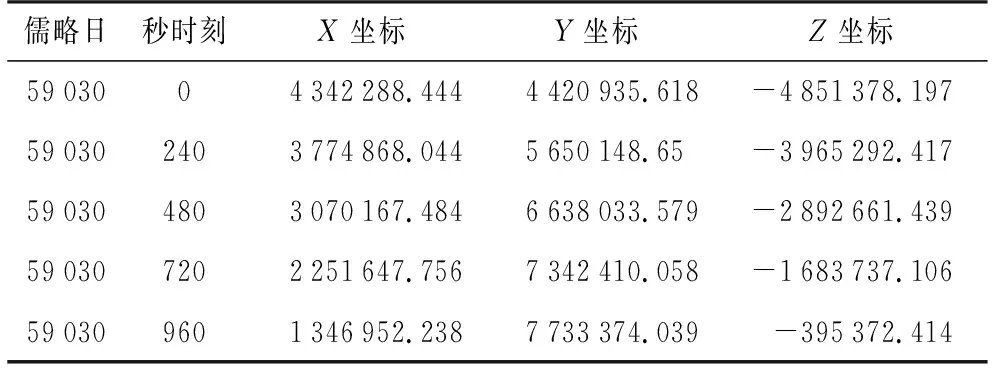
表1 AJISAI的部分SLR数据

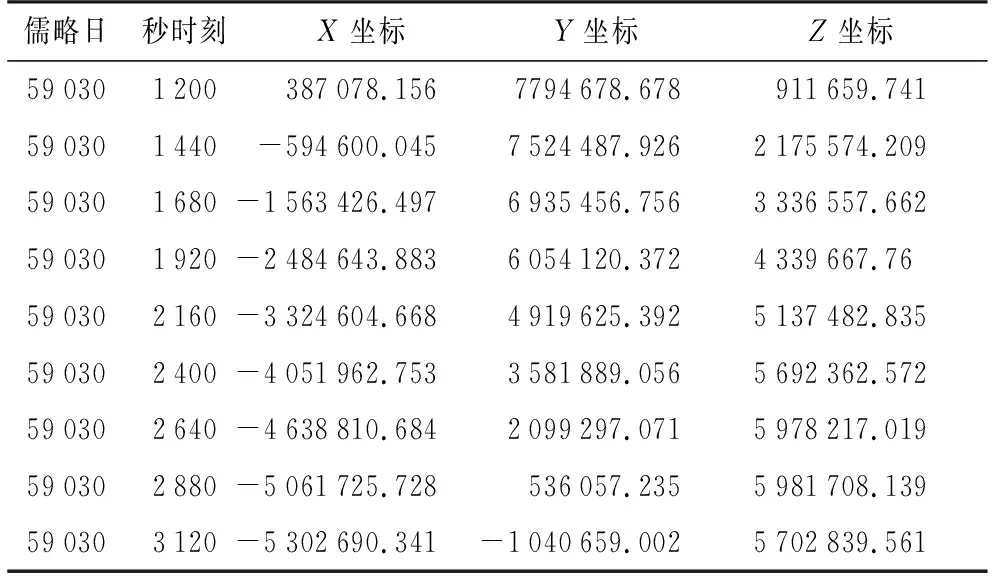
续表

选取n+1个互异的数据节点进行插值计算，通过拉格朗日插值算法可计算出一条n次多项式来近似目标轨迹的函数曲线，n即为插值的阶数。为验证插值精度，将数据中某一采样时刻作为待插值时刻，该时刻的坐标值按照真值作为对比，二阶插值时选取该时刻前2个时刻和后1个时刻的数据作为插值节点，三阶插值时选取该时刻前2个时刻和后2个时刻的数据作为插值节点，以此规律选择插值节点。

分析时选择6月30日5时56分为内插时刻，对比二阶样条插值、三阶样条插值和拉格朗日插值法在不同阶数时的插值精度，结果如图 1所示。

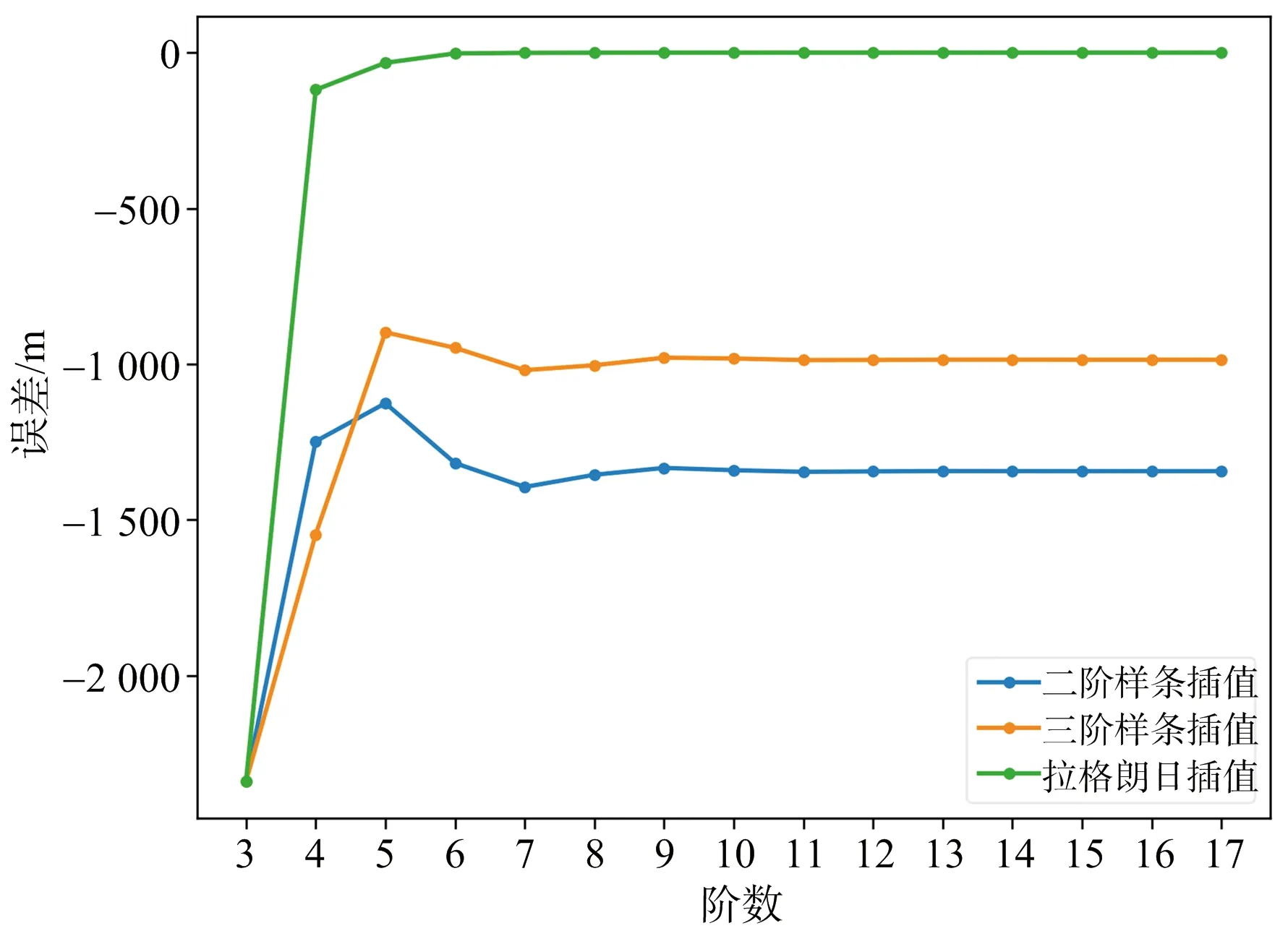
图1 三种插值算法的精度对比

从图1可以看出，样条插值法的插值误差在1 km左右，不满足雷达精度分析的需求，而拉格朗日插值法有远高于样条插值法的插值精度，使用拉格朗日算法对X,Y,Z三个方向上数据进行插值计算，结果如图2所示。

从图2可以看出，当插值阶数达到9阶时，拉格朗日插值法的插值精度可以达到厘米级，继续增加插值阶数，插值精度没有明显提高，反而增加了计算量，因此9阶拉格朗日插值算法为高效准确的SLR数据插值方法。

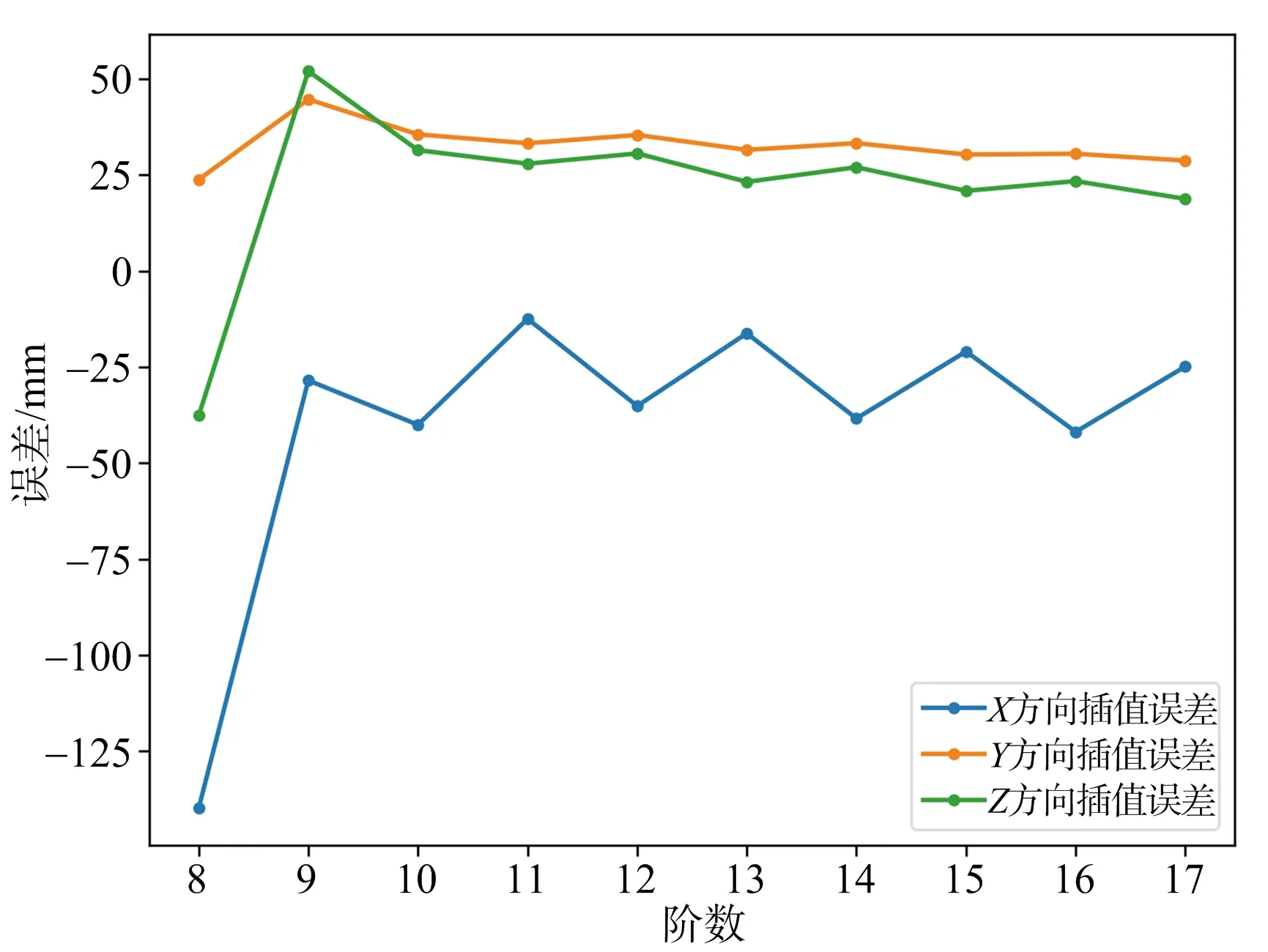
图2 X,Y,Z三个方向的拉格朗日插值误差

1.3 滑动式内插法

使用拉格朗日插值算法进行计算时，非滑动式的内插方法为使用已知的插值节点数据计算整段插值区间内的待插值点坐标，为分析非滑动式插值法的插值精度，选取6月30日5时40分至6时20分共11个采样时刻作为插值样本，依次将5时44分至6时16分共9个采样时刻作为待插值时刻进行插值误差计算，插值算法为9阶拉格朗日插值，X,Y,Z三个方向上的计算误差如图3所示。

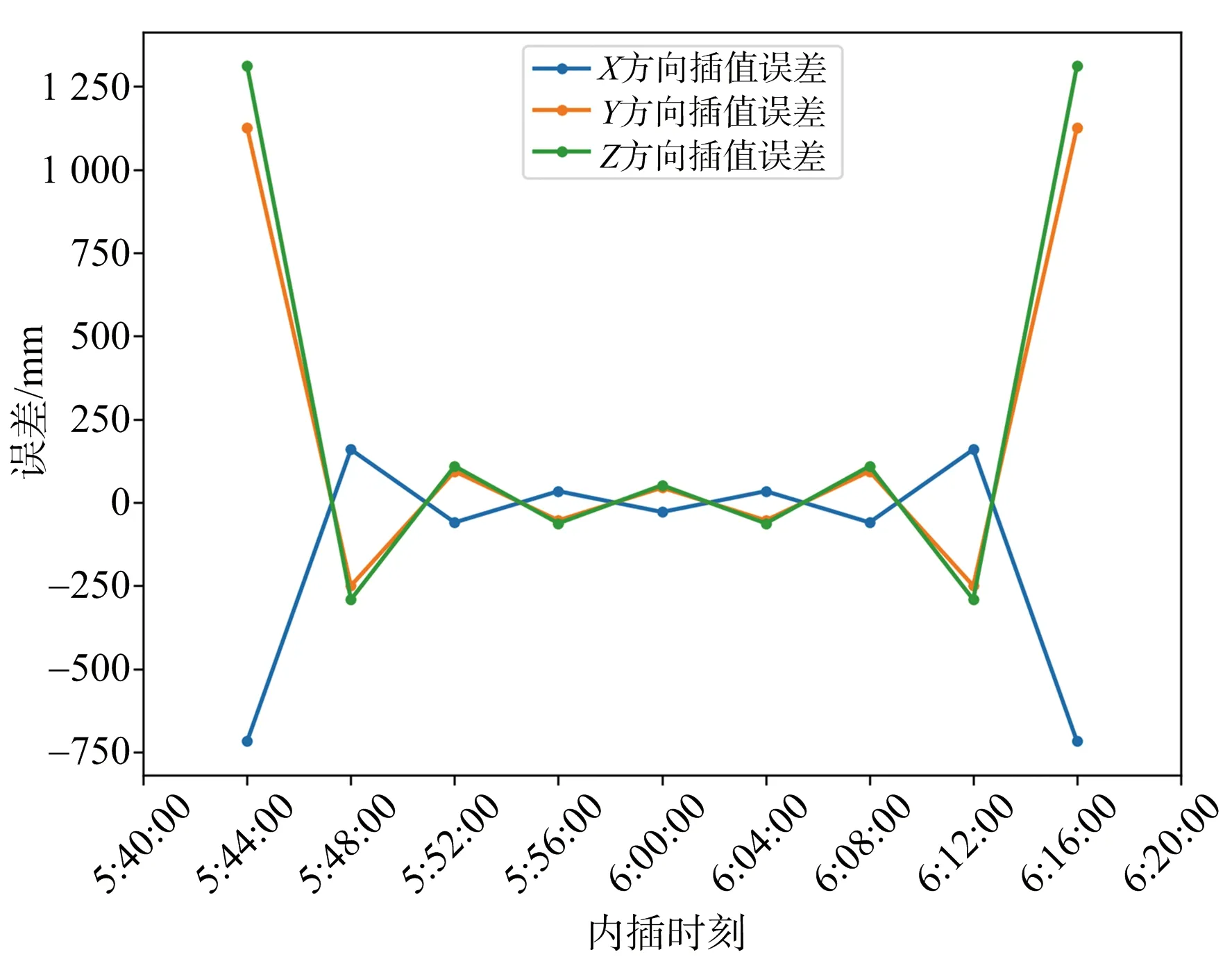
图3 插值区间内精度分析

从图 3可以看出，在靠近插值区间两个端点处的插值误差会增大，出现明显的波动现象，靠近插值区间中心位置的插值精度较好，因此，若能时刻保证待插值点处于插值区间的中心位置，则能整体得到精度较高的插值效果。这种通过不断变换插值区间，使得待插值点处于插值区间中心位置的方法，称为滑动式内插法[10]，配合拉格朗日插值算法，即为滑动式拉格朗日插值算法。

为进一步分析滑动式拉格朗日插值算法的插值精度，依次选取6月30日5时56分至7月2日11时56分的数据作为待插值节点，使用不同阶数的滑动式拉格朗日插值算法进行插值，计算插值误差与RMSE值，结果如表 2所示。

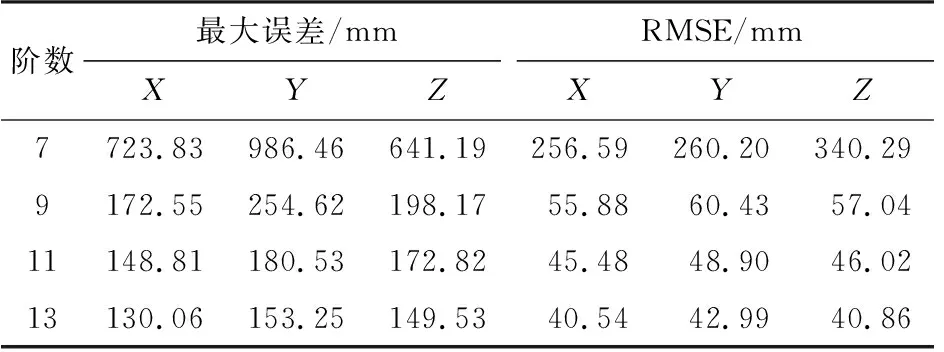
表2 不同阶数的滑动式拉格朗日插值误差

由表2结果可知，当插值阶数达到9阶时，滑动式拉格朗日插值法的插值均方根误差能够达到厘米级，最大误差值不超过30 cm，插值结果满足对雷达精度分析的需求。

2 雷达测量精度分析

通过滑动式拉格朗日9阶插值处理，已经得到与探测时刻相对应的空间目标高精度坐标值，但是此时的插值结果为空间目标在地心地固坐标系(ECEF)下的坐标，需要将其转换到站心坐标系下的球坐标数值，才能与雷达直接测量得到的距离、方位、俯仰信息进行对比，开展测量精度分析。

2.1 坐标转换

假设测站所在坐标点为P0=(x0,y0,z0)，经度、纬度、高程为LLA0=(lon0,lat0,alt0)，目标点坐标为P=(x,y,z)，如图4所示。

则目标在以测站为中心的站心坐标系下的直角坐标为

(3)

式中,

(5)

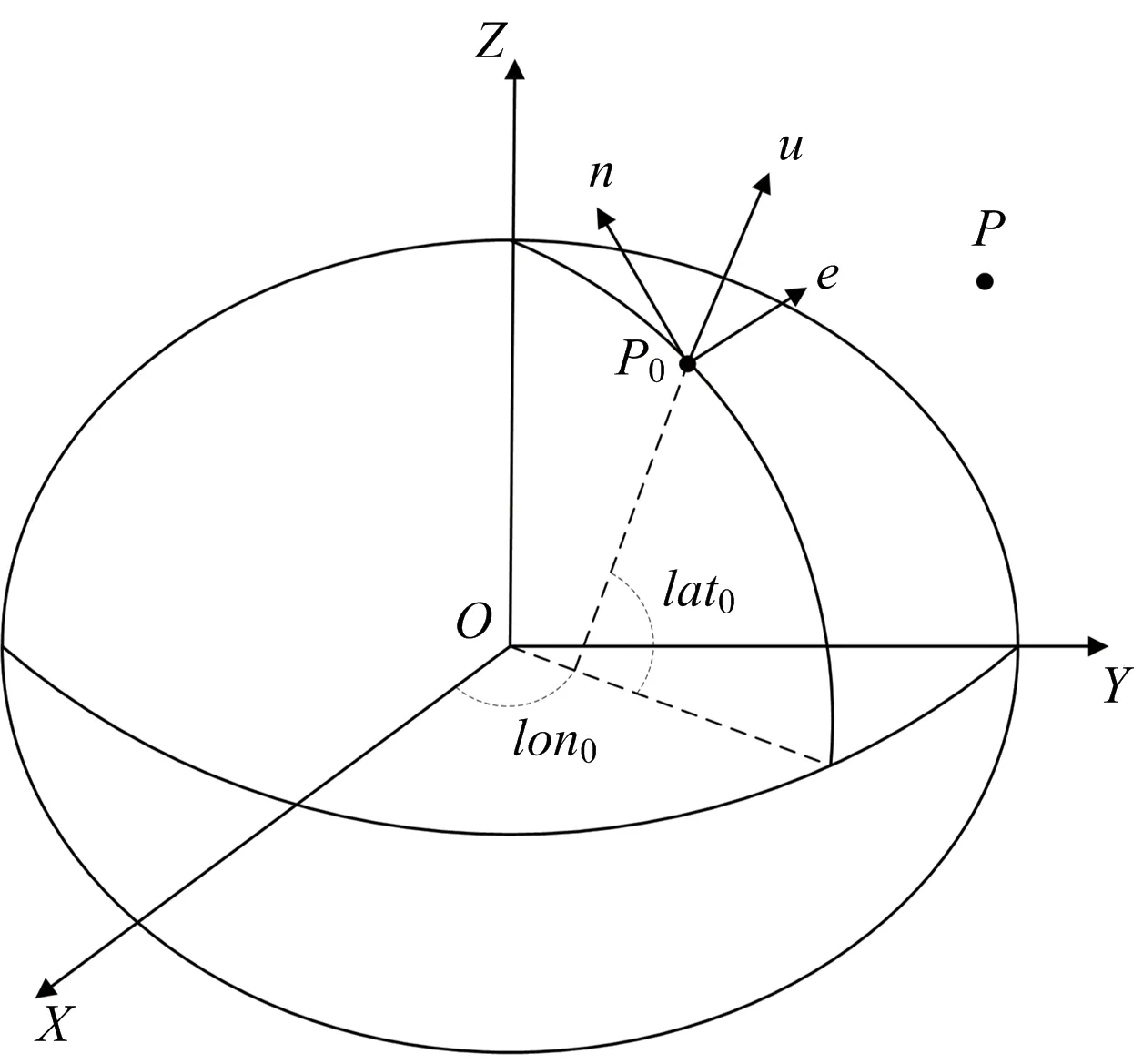
图4 ECEF与站心坐标系转换

最后，再将站心系下的直角坐标转换为雷达测量中常用的球坐标即可进行精度分析。

2.2 精度分析

在实际运用中，准确的精度分析对于掌握雷达效能状态有着重要的意义。经过滑动式拉格朗日9阶插值以及坐标转换的处理，具备极高定轨精度的SLR数据已经转换为雷达观测该目标时的参考值，位置误差在厘米级，可作为目标的准确位置进行比较。本文利用AJISAI的两行轨道根数进行过境预报，将预报结果添加部分噪声来模拟雷达的探测数据进行精度分析。

通过将探测结果中的方位角、俯仰角及距离数据分别与对应参考值进行作差处理即可获得雷达探测的精度信息，仿真计算结果如图 5所示。误差计算结果中可以清晰地看出雷达在探测目标时在方位、俯仰、距离三个维度上的测量误差，从而直观地掌握雷达的探测精度。

(a) 目标方位角探测误差

3 结束语

本文借助于SLR技术高测量精度的优势，利用其测量结果对空间目标监视雷达的探测结果进行了精度分析。通过对比研究几种插值方法，选取滑动式9阶拉格朗日插值算法对SLR数据进行处理，该算法兼具计算精度高、计算量小两个主要优势，插值结果符合雷达精度分析需求，同时还介绍了插值结果转换为站心坐标系数据的方法，方便进行雷达的探测精度分析。本文提出的精度分析方法原理简单，易于编程实现，为空间目标监视雷达的效能分析提供了技术参考。