低信噪比条件下直升机微动特征提取方法

张朝伟, 夏赛强, 杨 军, 刘建卫, 徐颖鑫

(空军预警学院， 湖北武汉 430019)

0 引 言

微多普勒概念由Chen引入到雷达观测领域，开创了基于微多普勒特征的雷达目标检测与识别新领域[1-4]。

带有螺旋桨部件的空中复杂运动目标，自身发生平动的同时伴随着螺旋桨的旋转运动，具有典型微动形式，被国内外学者广泛研究并不断深入，取得了一系列研究成果。时频分析方法[5-7]是一种最直观最常用的微多普勒特征分析方法，但其时频分辨率受窗函数的约束，存在分辨率和交叉项的矛盾问题。文献[8]联合时频分析方法和图像处理方法，提取出时频图中曲线特征来获得目标微动特征，但是在低信噪比条件下失效。文献[9]通过求取循环相关系数，实现了低信噪比条件下的微动特征提取，但是在闪烁情况下性能不佳。文献[10]研究了一种基于自相关处理的闪烁情况下微动特征提取方法，该方法运算量较大，信号重构能力弱，不易于工程实现。文献[11]研究了经验模态分解方法，将复杂的微多普勒时频曲线快速分解为多个模态分量，从分量中可以获得目标的运动参数，在提取进动目标微多普勒特征时具有优势，但是在发生模态混叠现象时，估计误差较大。文献[12-13]研究了高阶矩函数方法，通过对回波数据进行处理并计算其高阶矩函数来得到旋转频率和旋转半径的估计，具有计算复杂度小、运算速度快的优点，但抗噪性性能较差。文献[14-15]研究了正交匹配追踪方法，通过将信号在过完备原子库上稀疏分解来得到微动参数的估计，具有更为优良的鲁棒性，抗噪性能好，但随着估计参数的增加，运算量会急剧增加。

为解决信噪比适应性与估计精度和运算量的矛盾问题，本文以空中旋翼目标为研究对象，对其微多普勒效应进行建模仿真，深入分析微动特征参数的内在联系，并使用时频分析联合正交匹配追踪方法对微多普勒特征进行提取。仿真和实验结果表明，本方法能够实现低信噪比条件下旋翼目标微动特征的快速高精度提取。

1 旋翼目标回波模型

不失一般性，假设目标回波已完成运动补偿，建立雷达坐标系O-XYZ，如图1所示。仅考虑直升机主旋翼，该旋翼具有N个叶片，以转动角频率ω旋转，旋翼叶片长度为l，雷达到目标旋翼中心距离为R0，方位角为α，俯仰角为β。

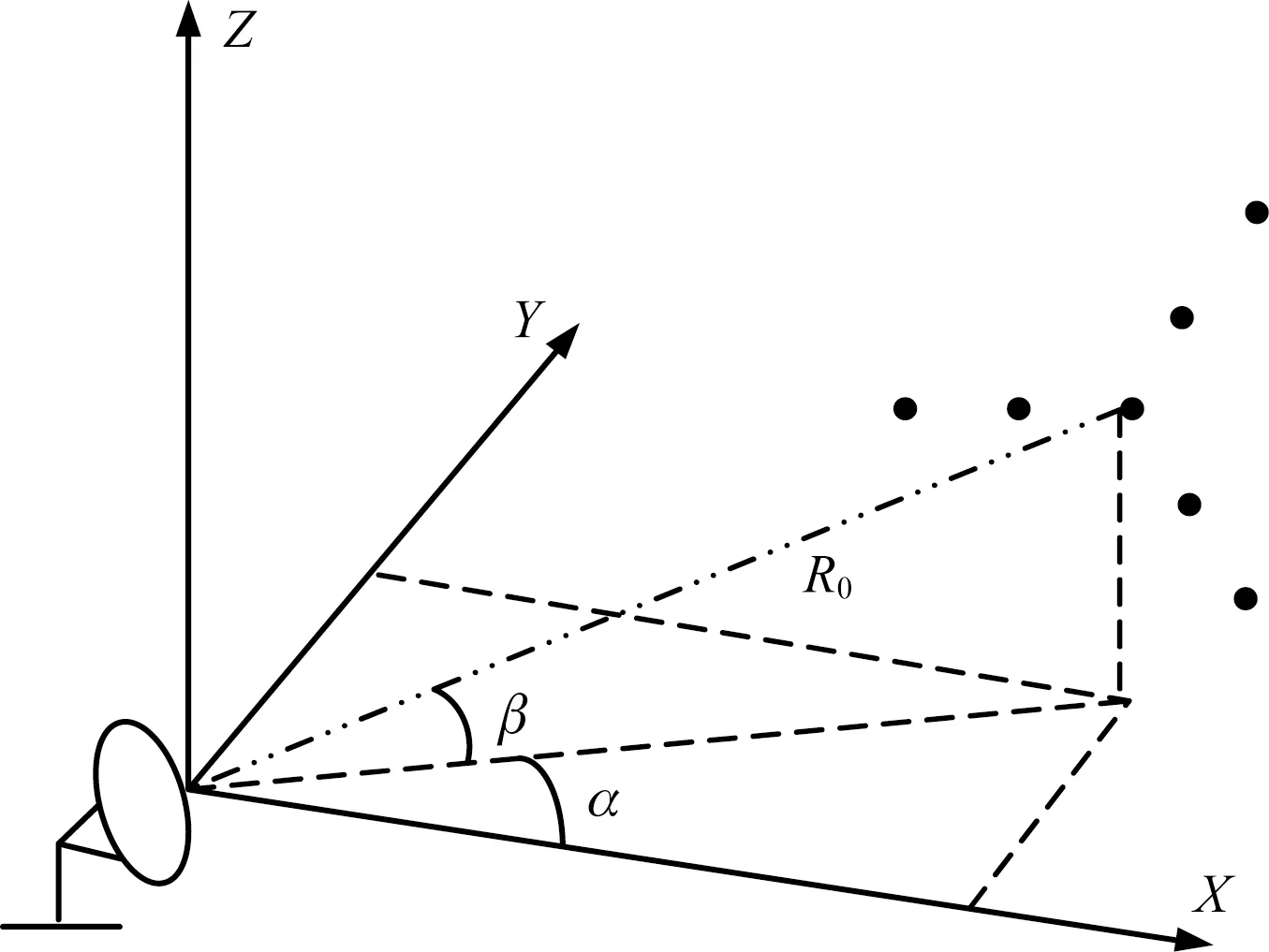
图1 散射点模型示意图

将叶片看作积分模型，进行单基地直升机旋翼建模，其运动补偿后回波[16]可表示为

(1)

式中，

(2)

(3)

σ为目标散射系数，λ为雷达波长，fr为目标旋翼转速，φ0为第一个叶片初相，整数k表示第k个叶片(1≤k≤N)。在式(1)可以看出，时域信号幅度受到sinc(·)函数调制，第k个叶片引起的瞬时多普勒频率为

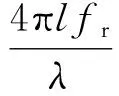
(4)

(5)

将式(5)代入式(3)可知该叶片的相位可表示为

(6)

两相邻闪烁之间的时间间隔满足

(7)

其中，%为取余数运算，当出现闪烁时，瞬时多普勒频率取到最大值：

(8)

2 目标闪烁参数估计

直升机旋翼回波的微多普勒呈现非线性变化，对于这类信号通常采用时频分析方法来揭示信号频率的时变特性。Gabor变换是一种常用时频分析方法，分辨率较好，且不存在交叉项[17]。将旋翼直升机回波信号变换到时频域：

(9)

其中，w(·)是高斯窗函数。旋翼微多普勒效应特征曲线在时频域表现为余弦调制曲线，在时域出现闪烁现象的时刻，在时频域会出现垂直于时间横轴的频率带，即时频域闪烁现象。

图2和图3分别是直升机叶片数为奇数情况和偶数情况下的闪烁现象示意图。从图2(a)和图3(a)可以看出，无论奇叶片数还是偶叶片数，在时域波形上并不能进行有效区分，但是在时频域，当直升机叶片数为奇数时，时频图中闪烁带交替出现，如图2(b)所示，当直升机叶片数为偶数时，时频图中的闪烁带则是同时出现，如图3(b)所示。

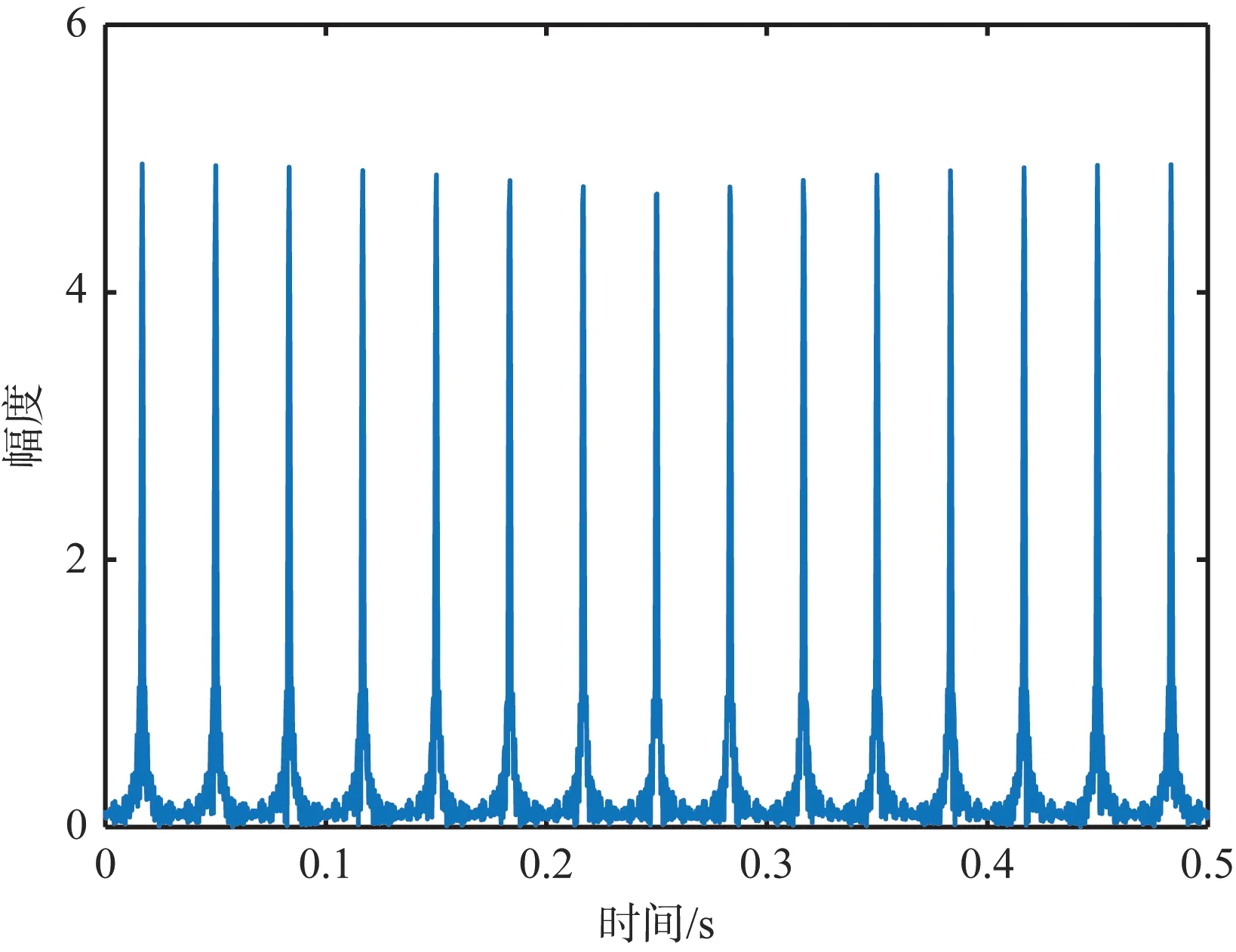
(a) 时域闪烁

(a) 时域闪烁

同理，将时频图数据幅值按频率进行累加，通过寻找峰值包络的宽度，可以计算得到目标微动的最大瞬时多普勒频率max。

由式(6)可知，叶片的相位与转速和叶片数密切相关。由式(7)知叶片的转速与叶片数和闪烁间隔密切相关。由式(8)知叶片长度与转速和最大多普勒频率密切相关。此时联立式(2)、式(6)、式(7) 和式(8)可得

3 旋翼目标参数估计

由式(1)知时域回波信号可分解为

(11)

式中，cm为原子系数，gm为第m个原子，Λ为待估计的参量，D为字典矩阵,D=[g1g2g3…gM]∈CNt×M，M为原子个数，Nt为采样点数，α∈CM为系数矢量，是稀疏的。将参数估计问题转化为最优gm范数问题进行稀疏向量求解，正交匹配追踪算法常用来解决该问题，通过构建字典矩阵，将信号在过完备原子库上进行稀疏分解，不断选取与信号最匹配的原子进行稀疏逼近，可实现低信噪比条件下的多微动参数估计。

由式(1)知直升机旋翼的回波信号由参数(fr,N,φ0,l)确定，同时对4个参数进行估计将会导致运算量大幅提高，且估计精度也会受到影响，若将已估计得到的目标闪烁参数作为先验信息，那么时域回波仅由N确定，叶片数通常在3～8个，且为整数值，大大减少了估计难度，运算量减少了Cfr·CN·Cφ0倍。由OMP算法原理可知，字典中原子可通过待分解信号的内在特性来构造，目标微多普勒信号是一个正弦调频信号，因此选择SFM原子来构造过完备原子库，第m个原子可表示为

(12)

式中，m=pNt。对原子集里每个原子进行归一化处理，即

(13)

算法实现流程[18-19]如下：

输入： 测试样本r0=s，训练字典D=[g1g2g3…gM]，稀疏度K。

初始化： 初始化残差余量r0=s，匹配原子集赋空值Λ0=∅，匹配原子记录矩阵赋空值D0=∅，迭代初始值k=1。

2) 将寻找到的最相关字典元素的索引λk加入匹配原子集Λk=Λk-1∪{λk}；

4 仿真分析

为了更清晰地分析本文方法对旋翼目标参数的估计性能和可行性，参考当前窄带雷达系统的相关参数确定雷达仿真参数，并选取两种常见直升机的真实参数作为目标仿真参数，脉冲压缩后信噪比为10 dB，仿真雷达参数设置如表1所示，仿真目标参数如表2所示。

表1 雷达参数

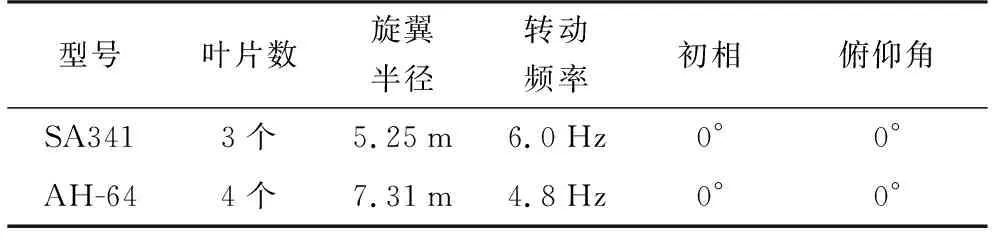
表2 目标参数

利用SA341直升机真实参数进行仿真，其仿真结果如图4所示。从图4(a)可以清晰观察到正负频率部分的时频图幅值纵向积累曲线峰值交替出现，即可判断出目标叶片数目为奇数，且曲线相对于时域闪烁曲线更加平滑，有利于寻找峰值点位置，此时第一个闪烁时刻为0.014 s，为负频率闪烁，第十八个闪烁时刻为0.486 s，为正频率闪烁，通过这两个时刻可以估计出闪烁间隔时间为(0.486-0.014)/17=0.027 8 s，通过首尾两个闪烁时间差求平均值的方式求取闪烁间隔相比于直接计算相邻两个闪烁时间差作为闪烁间隔的方式更为精确。图4(b)是时频图幅值横向积累曲线，由于时频图中曲线具有一定宽度以及一定的边缘效应，导致图中曲线具有明显的上升沿和下降沿，且持续时间较长，不利于寻找最大瞬时多普勒频率数值，对于这类信号，通常采样3 dB宽度来衡量其包络的宽度，此时估计出目标最大瞬时多普勒频率为1 315 Hz，与理论值1 319.5 Hz基本一致，误差为0.34%。将估计得到的第一个闪烁时刻、闪烁间隔和最大瞬时多普勒频率作为先验信息，利用OMP方法估计叶片数，结果如图4(c)所示，可以看出在叶片数为3时取到最大值，与预设值一致。利用式(7)可估计出目标叶片转动频率为5.995 2 Hz，与预设值误差为0.08%，利用式(8)可估计出目标旋翼半径为5.236 4 m，与预设值误差为0.26%。

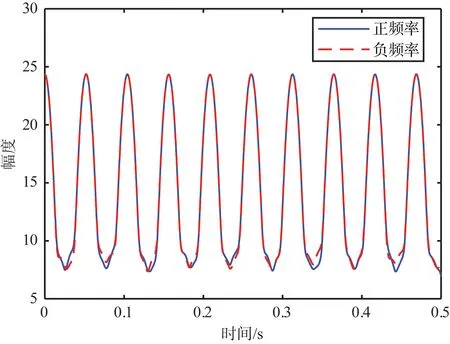
(a) 时频图幅值纵向积累曲线

AH-64直升机仿真结果如图5所示。从图5(a)观察到正负频率部分的时频图幅值纵向积累曲线峰值同时出现，即判断目标叶片数目为偶数，此时第一个闪烁时刻为0 s，第十个闪烁时刻为0.468 6 s，估计出闪烁间隔为(0.468 6-0)/9=0.052 s，从图5(b)中估计出目标最大瞬时多普勒频率为1 468 Hz，与理论值1 469.8 Hz基本一致，误差为0.12%。图5(c) 是利用OMP方法对叶片数的估计结果，在叶片数为4时取到最大值，与预设值一致。此时，目标叶片转动频率估计值为4.807 7 Hz，与预设值误差为0.16%，目标旋翼半径估计值为7.289 5 m，与预设值误差为0.28%。

(a) 闪烁参数

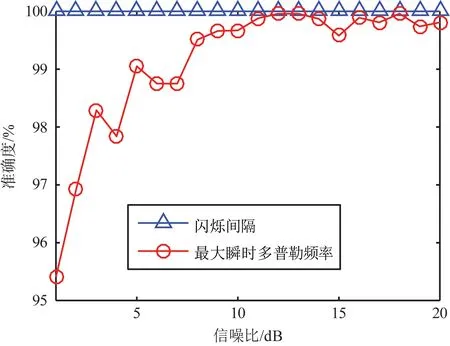
从以上两组仿真可以看出，本文方法能够较为准确地估计出目标的旋翼参数，在信噪比为10 dB情况下，其估计误差小于0.3%。以SA341仿真为例，图6给出了不同信噪比情况下其目标闪烁参数估计精度和旋翼参数估计精度。从图6(a)可以看出，闪烁间隔被准确估计，而最大瞬时多普勒频率估计准确度随信噪比的降低整体上呈现下降趋势，且在信噪比小于8 dB时下降较为明显。在图6(b)中，叶片长度估计准确度曲线与图6(a)中最大瞬时多普勒频率估计准确度基本一致，这是由于在估计叶片长度时使用了最大瞬时多普勒频率估计值，导致估计误差向下传递。同理，目标转动频率估计值与叶片数估计值和闪烁间隔估计值息息相关，而这两个参数估计准确度在不同信噪比条件下均能保持很高的准确度，因此目标转动频率估计较为准确。实际上，OMP算法对网格匹配程度要求较高，一旦网格失配就会导致叶片数估计不准确，从而导致转动频率和叶片长度估计失败，通过仿真发现OMP算法对闪烁间隔估计准确度的要求要远高于瞬时多普勒频率估计准确度，即式(10)中sin(·)函数项相比其系数对OMP算法性能的影响更大。

5 实验分析

为验证本文方法在实测数据中的有效性，利用一组实测数据进行微动特征提取实验，辐射源为某型窄带雷达，目标为某型直升机，其公开参数为叶片数5个，叶片长度8.6 m，旋翼转动频率4 Hz。

在实测数据中，目标直升机背站飞行，且外场环境存在强地物杂波，因此需要对回波进行杂波抑制和运动补偿，其结果如图7所示。图7(a)为杂波抑制后的时域回波，能够观察到幅度不一的时域闪烁现象，其中幅度相对较强的闪烁共计出现七次。对时域回波进行运动补偿并变换到时频域，结果如图7(b)所示，时频闪烁现象明显，在[-300 Hz,-600 Hz]范围内还存在覆盖范围较广的调制频带，这是由于叶毂跟随叶片一起旋转以及尾桨旋转导致的，但是叶毂和尾桨相对主旋翼而言具有尺寸小，转动半径小的特点，其微多普勒频率较低，且没发生闪烁现象，从而不会影响本文方法对直升机叶片的特征提取。

图8是本文方法的特征提取结果，从图8(a)可以观察到正负频率部分的时频图幅值纵向积累曲线峰值交替出现，即判断目标叶片数目为奇数，此时第一个闪烁时刻为0.161 s，最后一个闪烁时刻为0.315 s，估计出闪烁间隔为0.025 7 s，在图8(b)中正负频率上的最大值并不严格对称，这是由于目标姿态导致的，此时对其取均值估计出目标最大瞬时多普勒频率为1 396 Hz，图8(c) 是利用OMP方法对叶片数的估计结果，叶片数估计值为5。将上述三个参数估计值带入公式进行计算，目标叶片转动频率估计值为3.891 Hz，与目标公开参数误差为2.72%，目标旋翼半径估计值为8.565 m，与目标公开参数误差仅为0.41%。

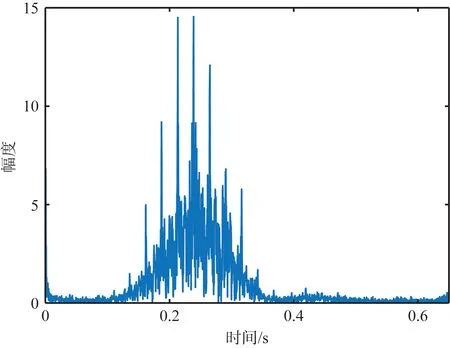
(a) 时域波形

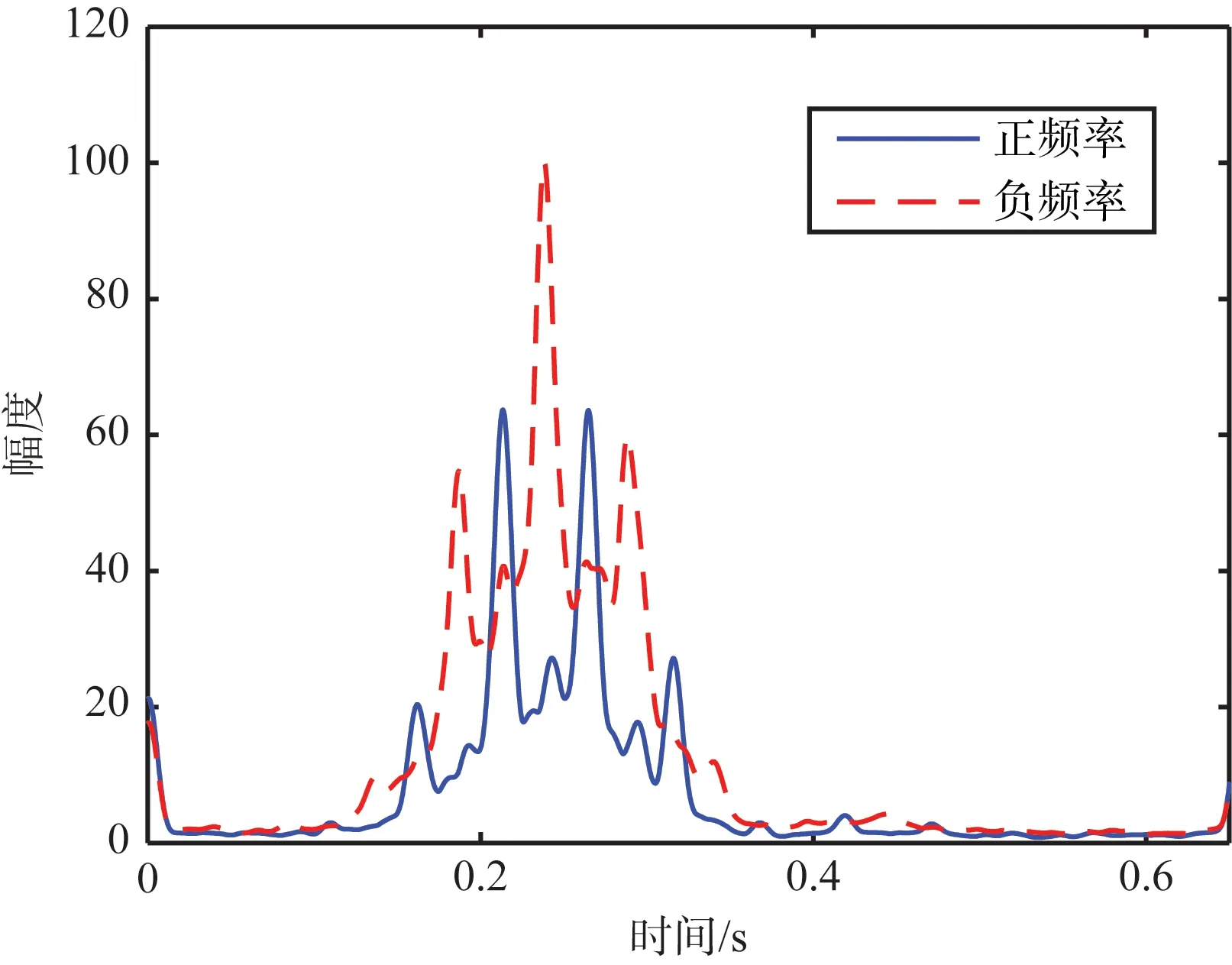
(a) 时频图幅值纵向积累曲线

6 结束语

本文从目标微动特性出发，提出了一种低信噪比条件下的直升机微动特征提取方法。通过对直升机回波进行Gabor变换，获取其时频信息，采用时频图幅值积累法较好地获取旋翼回波闪烁参数，如叶片奇偶数、闪烁周期和最大瞬时多普勒频率。并将其作为先验信息，对稀疏字典中原子进行降维处理，将多参数搜索优化为单参数搜索，极大地降低了正交匹配追踪算法的运算量，叶片数估计准确度在网格不失配情况下达到100%，其目标叶片数和转动频率估计准确度达到99.9%，叶片长度估计准确度受最大多普勒频率估计误差传递的影响，能够保持在95%以上，且在低信噪比条件下保持优良的鲁棒性。实验结果表明本文方法具有较强的实用性，为后续直升机目标识别奠定了基础，具有一定的工程应用价值。