基于波形聚类分析的微地震事件成像研究

李德伟杨瑞召孟令彬

中国矿业大学(北京)地球科学与测绘工程学院,北京 100083

微地震事件定位面临两大难题,一是发震时刻难以确定,二是微地震事件的信号难以识别[1]。相对于井中采集的信号,地面检波器阵列通常信噪比较低,原因主要是震源到地面检波器距离较远,导致子波衰减严重,其次是地面观测阵列更容易受噪声(施工噪声、环境噪声等)影响[2]。

为了克服这两大难题,微地震震源定位发展了两类方法,一类是震源成像的方法,另一类是基于微地震事件振幅叠加方法[3-4]。振幅叠加或网格搜索方法,是将储层一定区域内划分为大小相同的网格,根据速度模型计算每个网格到所有检波器的走时,得到所有网格点到全部检波器的走时表[5]。根据走时表的时差关系或利用波形的互相关,提取走时差进行偏移叠加数据道波形,从而反演储层区域的成像结果,成像结果的最大值位置即为震源位置。该方法的优点是,无须识别、拾取初至即可进行对地下目标范围和地震记录进行扫描,完成震源的成像结果[6]。但通常叠加的数据不会进行筛选,导致噪声干扰数据参与运算,降低了成像效果。同时,不同的震源机制(ISO 源、DC 源、CLVD 源)会辐射不同的波场特征,地面不同位置检波器观测到的P 波和S 波特征也不相同[7]。在叠加成像过程中,低信噪比和信号特征差异都会对成像结果造成影响。

本文应用了一种聚类分析方法消除这种影响。聚类分析又称为群分析,它是研究(样品和变量)分类问题的一种多元统计方法,并对相似属性特征的对象进行分组的数据挖掘方法[8]。正如统计学中样本之间有不同的分类方法,信号也可以看作是等间隔、连续采样的样本。通过聚类分析可以定义信号与信号之间的距离,距离越小,信号差异越小；反之,差异越大。根据不同信号的特征对信号进行聚类计算,筛选出信号特征接近的数据集进行成像,改善成像的质量。相比于传统波形互相关计算,聚类分析对地震道噪声敏感性更低,不易受噪声影响。波形互相关计算需精确提取事件的完整波形才能计算出较为精确的相似性结果,而聚类分析只需包含事件本身就可对其进行分类。

1 波形聚类方法

波形聚类方法主要包括数据道之间的距离计算方法和聚类算法。

学者提出多种距离计算方法,如欧氏(Euclidean)距离、切比雪夫(Chebychev)距离、兰氏(Canberra)距离、马氏(Mahalanobis)距离、夹角余弦(Cosine)距离以及汉明(Hamming)距离等[9]。每种距离计算适用不同的样本特点,尝试以上方法对微地震数据进行了测试,发现欧式距离能获得不错的聚类结果。欧氏距离计算方法如下:

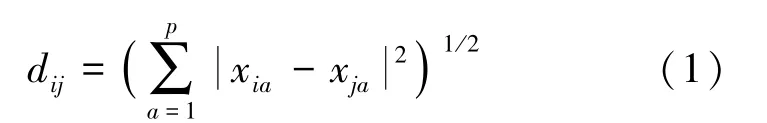
式中,dij为数据道Xi与数据道Xj的距离；P为数据道中采样点总数；xia、xja分别为数据道Xi与Xj中第a个采样点位置的振幅值。

定义dij有如下性质:dij≥0,dij=dji且dij≤dik+dkj。欧式距离计算结果与波形数据的量纲有关,因此在计算前需要对各道数据进行归一化处理。通过式(1)可得距离矩阵D(0):

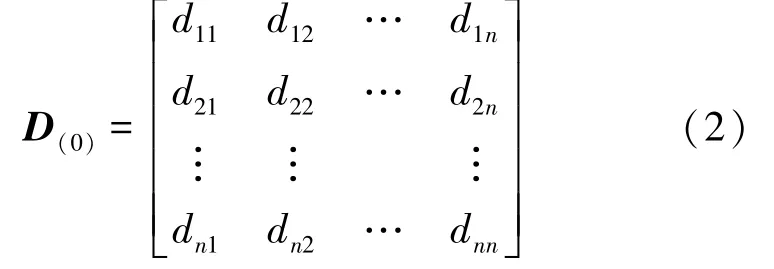
式(2)中,d11=d22=…=dnn=0,D是一个对称矩阵,在聚类时只需计算上三角或下三角形部分即可。根据D(0)可对n道数据进行分类,距离近的数据归为一类,距离远的数据归为另一同类。

聚类也有多种方法,如最短距离法、最长距离法以及重心法等。本文采用最短距离法来说明聚类的过程:

(1) 确定距离的计算方法。计算波形数据之间的距离,得到距离矩阵D(0),定义类与类之间的距离为Dij,开始时每道数据自成一类,显然此时Dij=dij。

(2) 找出D(0)的非对角线最小元素,设为dpq,则将波形数据道X(p)和X(q)合并成一个新的类,记为Gr={X(p),X(q)}。

(3) 计算所有剩余类Gk与新类Gr的距离:

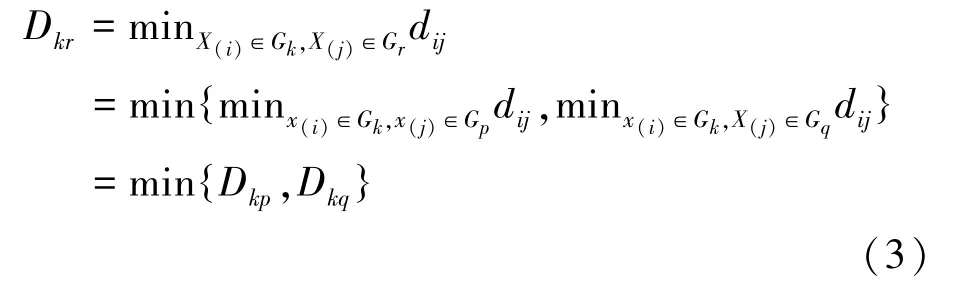
(4) 将D(0)中p、q行及p、q列删除,然后在D(0)的第一行第一列位置插入Gr,得到一个n-1维距离矩阵,记为D(1)。

(5) 对D(1)重复步骤(2)(3)(4)得到D(2),直到所有的元素归为一类(距离矩阵中剩下一行一列)时,聚类结束。

2 聚类分析的应用

2.1 正演数据聚类

现以合成波形数据为例,说明波形聚类的过程。图1(a)(c)(e)(g)分别为Ricker 子波、Morlet子波、偏移的Morlet 子波以及以上3 种子波叠加的波形。微地震事件在发震时频率很高,传播过程中衰减严重[10-12],因此分别对4 种子波叠加高斯白噪声模拟真实的信号,如图1(b)(d)(f)(h)所示。可以看出,叠加噪声后的合成信号信噪比很低,波形特征较为接近。

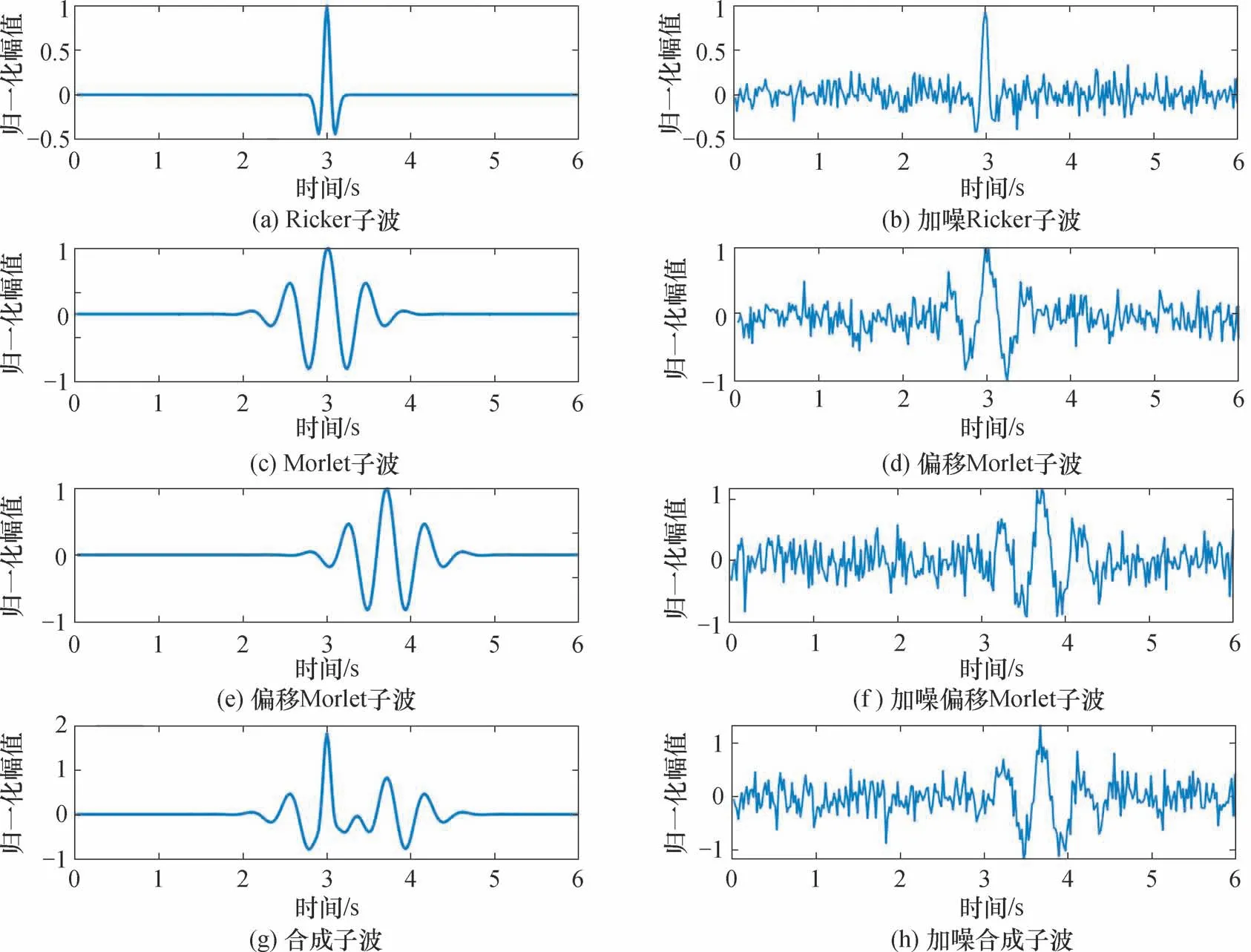
图1 4 种类型子波与对应加噪后合成波形Fig.1 Four types of wavelets and the corresponding synthesized waveform with noise

对4 种不同的子波分别叠加3 次高斯白噪声,如图2 所示。每次叠加噪声均为随机叠加,因此叠加噪声后波形各不相同,将12 道合成数据随机打乱,其中1、5、9 道为Ricker 子波合成波形,2、3、8道为Morlet 子波合成波形,4、6、10 道为偏移Morlet子波合成波形,7、11、12 道为合成子波合成波形。

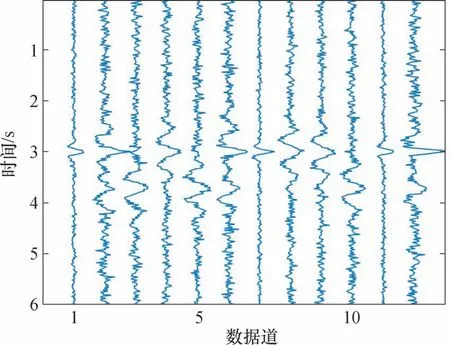
图2 随机打乱后的合成数据剖面Fig.2 Synthetic data traces after random order

聚类结果如图3 所示。根据式(1)计算各道之间欧式距离,得到距离矩阵,在初始状态下每一道各为一类。第1 步,查找各类之间的最小距离,将1、9 合并为一个类；第2 步,重复计算新类和剩余类的距离,将最小距离的5 和1、9 合并为新的类1、9、5。重复上述2 个步骤后,2、8、3 与4、10、6 各分为同一类。分类结果中只有7 没有与11、12 直接归为同一类,这是由于7 前面组合的新类较为相似。分类结果表明,聚类方法基本能将12 道合成波形数据正确分类。

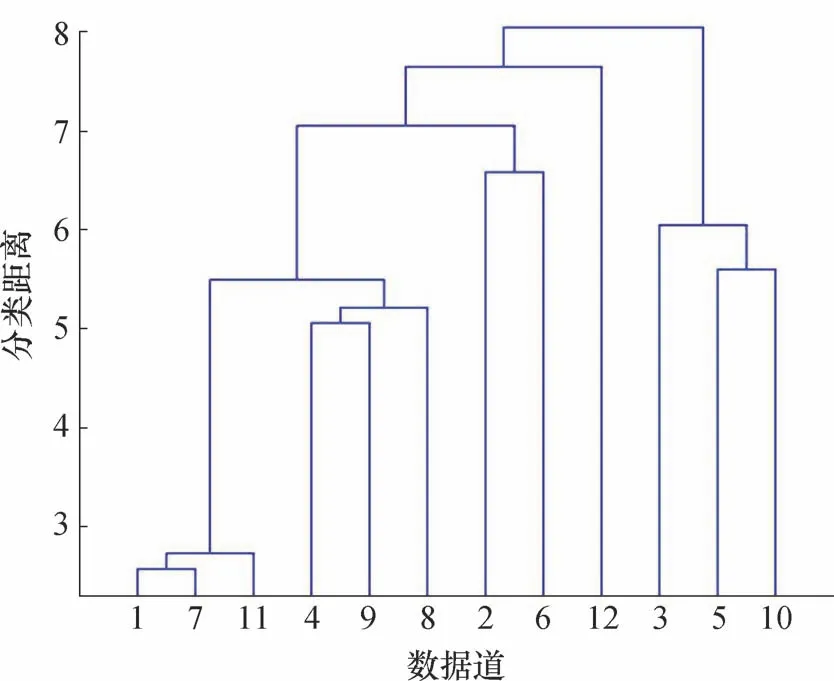
图3 合成数据聚类结果Fig.3 Clustering results of synthetic data

2.2 微地震信号聚类

将聚类分析方法在事件微地震监测数据中进行了应用。M 井组位于山西省临汾市沁水县马壁乡(沁水盆地南部),该井组为水平井,水平井段垂直深度在920 ～1 030 m 之间。该地区主要煤层为3 号煤,煤层深度由东南向西北方向逐渐变浅,煤层厚度2.4 ～7.5 m,水平井段附近无显著大断层发育[13-14]。根据声波测井曲线计算,储层P 波速度为3 300 ～3 500 m/s,地表速度较高,P 波速度为3 900 ～4 200 m/s。煤样测试表明,3 号煤层渗透率在0.025 ～0.029 mD 范围,整体渗透性较差。

M 井组进行了水力压裂改造,以扩大煤储层的煤层气产量,同时地面进行了微地震监测。微地震监测观测系统地面投影如图4 所示,其中黄色图钉表示检波器位置,红色图钉为水平井段起始位置,绿色图钉为井底,红色实线为井轨迹。

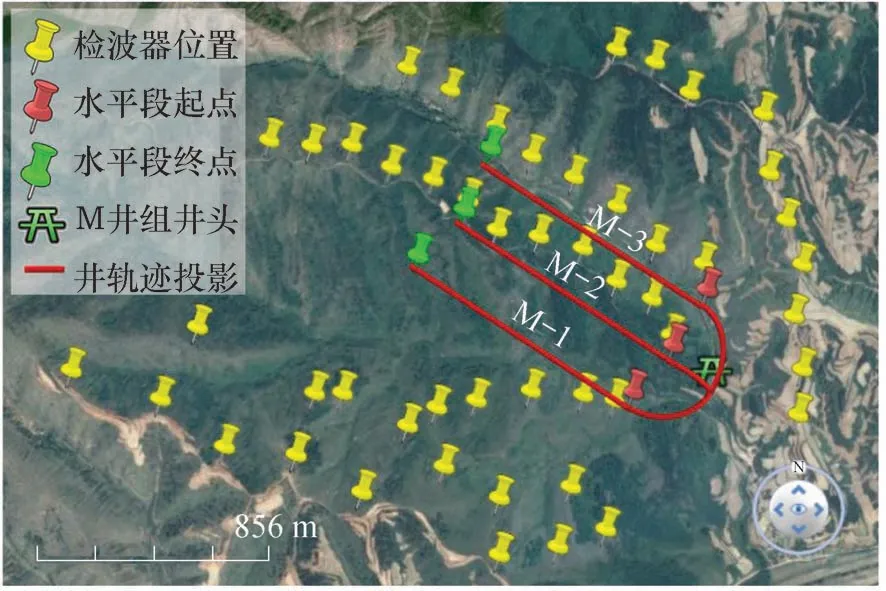
图4 M 井组地面微地震观测阵列与井轨迹地面投影Fig.4 Geophone array of well M group and ground projection of well trajectory

M-1 井第5 段水力压裂地面微地震监测事件A 波形如图5 所示,数据记录共43 道,时窗内共800 采样点,采样频率2 ms,波形显示时窗的长度为1.6 s。从波形图中可以看出,2、14、25 为明显的噪声干扰道。此外,由于地面检波器分布位置不同,波形特征存在明显的差异。

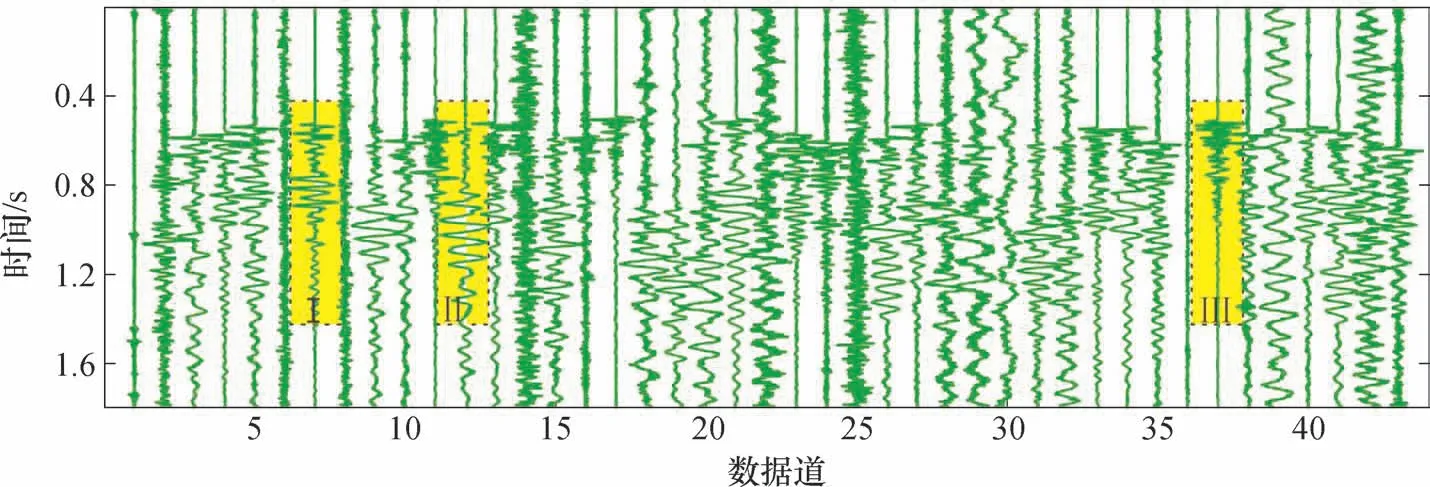
图5 地面监测微地震事件A 波形Fig.5 Waveform of surface microseismic event A

对图5 的微地震进行聚类分析,结果如图6所示。横轴坐标对应图5 中的数据序号,纵坐标表示分类距离。由于数据较多,为了能清晰地看出聚类结果,分类距离从左至右依次增大。根据分类结果中距离的变化趋势可以看出,矩形内数据道之间的距离差值较小,变化梯度低；矩形框外的数据道相对距离变化较大,因此矩形框内的数据道可以看成一类事件。选取图6 中蓝色虚线矩形框内的数据进行叠加定位。保留的数据波形都具有相似的波形特征,如较强的P 波或S波。去除数据道波形为噪声道或信号差异较大的数据波形。

图6 事件A 聚类结果Fig.6 Clustering result of event A

从图5 的波形数据中提取3 类典型特征的微地震信号,如图7 所示。

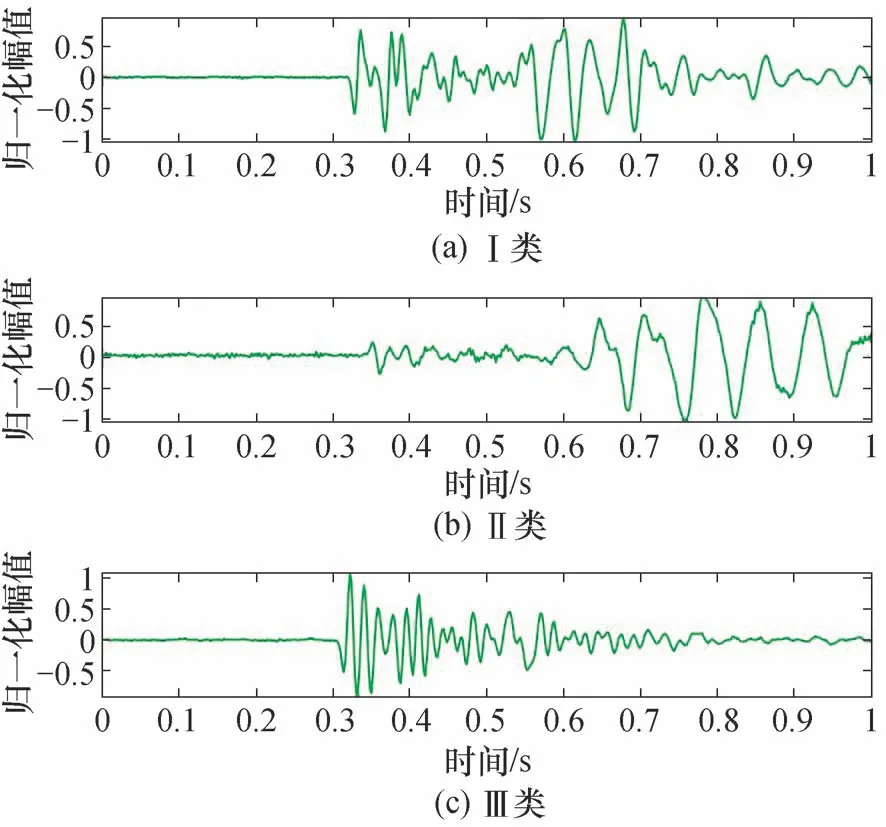
图7 事件A 中3 种不同信号特征Fig.7 Three different signal characteristics in event A

Ⅰ类信号特征具有明显P 波和S 波,且P 波波动明显；Ⅱ类信号无明显P 波,但S 波振幅较强；Ⅲ类信号具有较强的P 波,而无明显的S 波。3 类信号主要由震源机制与地面采集位置确定。由于基于振幅叠加的微地震事件成像方法与波形特征密切相关,噪声干扰道以及不同信号特征会影响最终的成像结果,因此在波形叠加过程中,一般采用绝对值振幅或平方振幅值[15],Ⅰ类和Ⅲ类可避免极性相反造成的振幅相互抵消,但Ⅱ类在P 波振幅叠加中不可避免地带来振幅削弱的影响。利用波形之间的相关性,去除了Ⅱ类数据,最终保留的数据道如图8 所示。

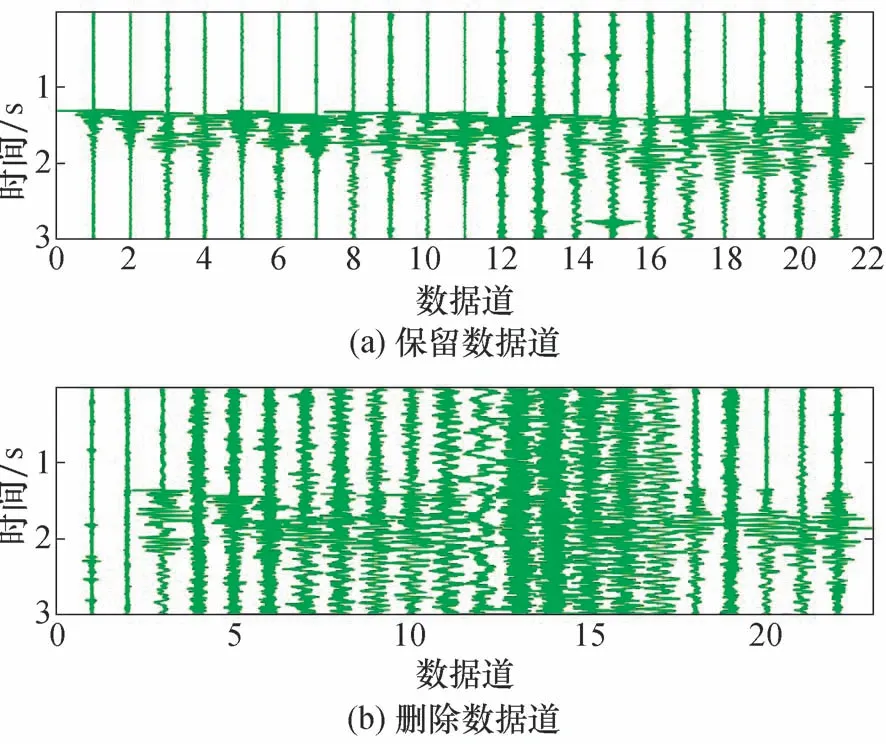
图8 事件A 聚类后保留数据与删除数据波形Fig.8 Retained traces and deleted traces after event A clustering

2.3 信号聚类对定位成像的优化

分别对聚类筛选前后的数据道进行绕射叠加成像。绕射叠加的原理是,通过射线追踪算法计算同一个震源点到每一个检波器的时间偏移量,当不同检波器校准偏移量为同一发震时刻时,振幅叠加必然最大。其定位基本流程是,将目标区域按定位精度划分成多个小体元(假设震源点),计算体元到每个检波器的偏移量,然后沿着偏移量进行绕射叠加,直至遍历所有体元。其成像公式[16]为

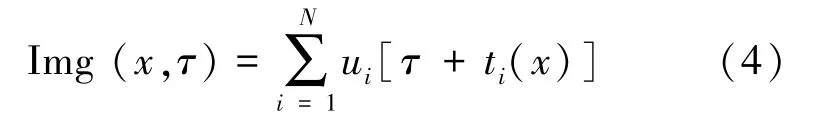
式中,N为检波器个数；ui为第i个检波器记录的地震记录,即原始波形信息,通常为波形振幅的绝对值或振幅平方；ti(x)为从体元到第i个检波器的理论到时；τ为发震时刻。

整个成像过程是将所有检波器波形记录上的振幅按照计算的走时进行叠加,在震源位置的网格点处叠加能量最强。

分别对聚类前后的数据进行绕射叠加成像。由于已知微地震事件所在位置,叠加时选取600 ms 时窗长度进行绕射叠加。全部波形数据成像结果如图9(a)所示,聚类后保留数据成像结果如图9(b)所示。背景颜色为相似性叠加值,红色表示高相似性值,黄色、绿色依次降低,蓝色最低。根据叠加成像的原理,一个震源点释放的地震波信号由地面各站点接收后虽然有时差、振幅差或畸变[17],但是具有内在相关性。绕射叠加成像结果中最大能量值位置即是震源发生的位置[18-19]。聚类分析的本质是增加事件的成像值,改善定位结果。

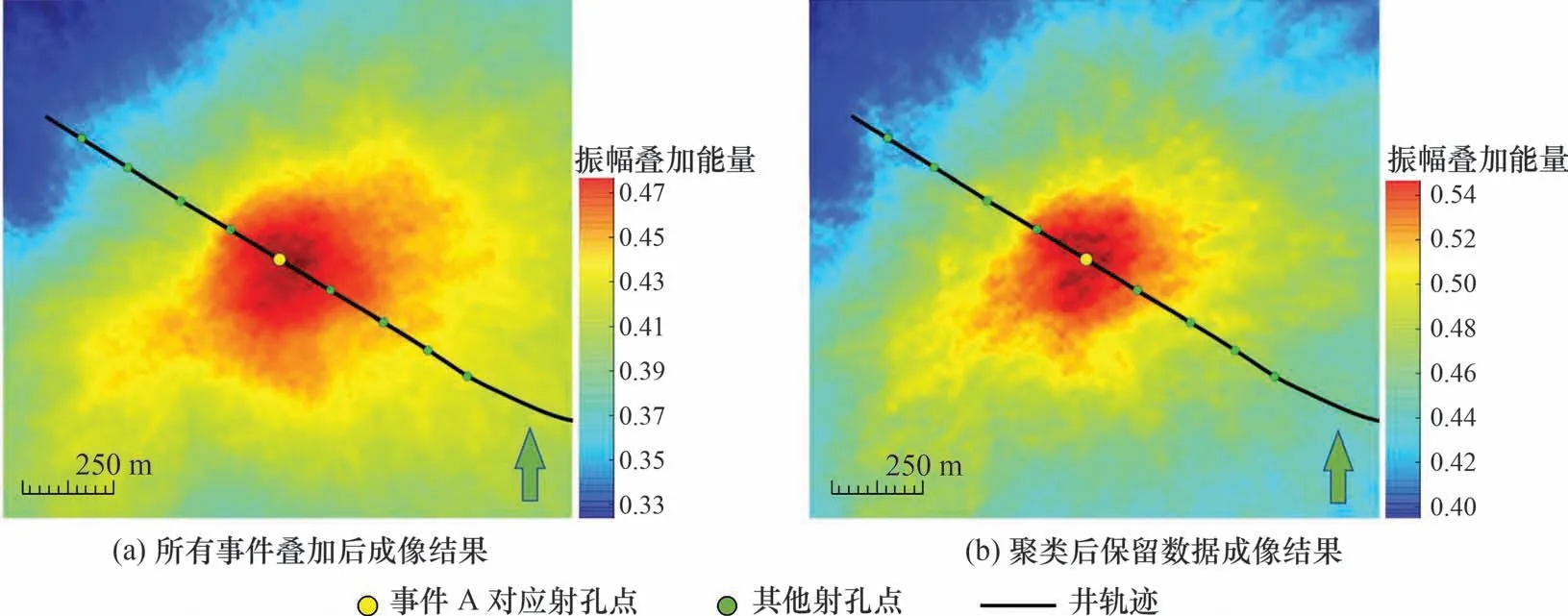
图9 事件A 成像结果对比Fig.9 Comparison of imaging results of event clustering

对比聚类前后可以看出,图9(b)成像结果相比图9(a)更加聚焦,红色区域过渡更集中,并且聚类保留数据的相似性值域明显提高(全部数据叠加相似性值域为0.33 ～0.47,筛选后数据叠加相似性值域为0.40 ～0.54),从而提高了定位结果的可信度。在成像结果中,只需提取对应的最大相似性值位置或拓扑结构的中心,便可确定震源点[20]。因此,聚类筛选后的数据在成像效果和相似性值域均得到了明显改善,有利于微地震事件的进一步分析。

事件B 与事件C 的微地震事件成像结果如图10、图11 所示。可以看出,聚类分析方法改善了成像的质量,提高了相似性值域范围。

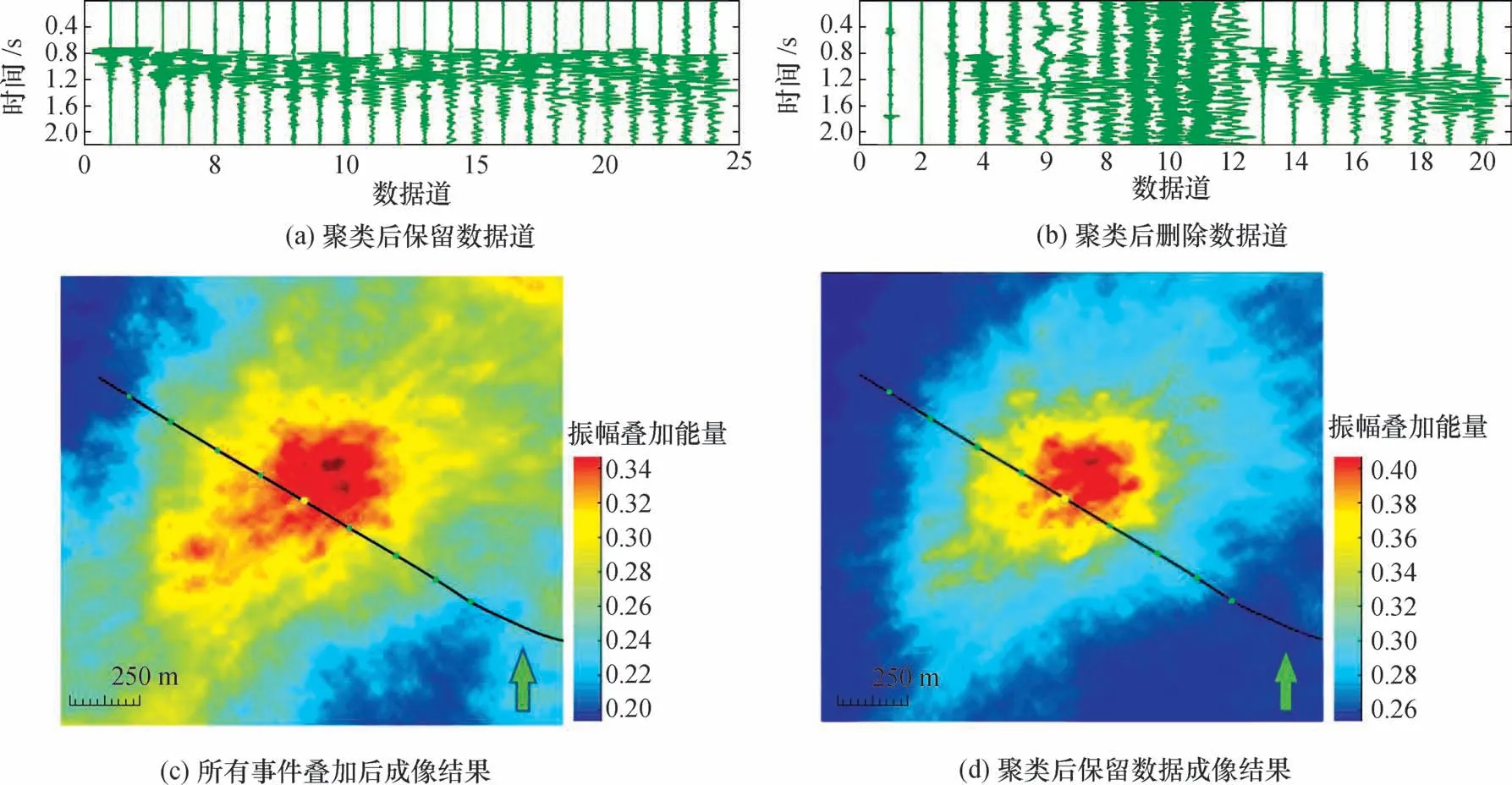
图10 事件B 成像结果对比Fig.10 Comparison of imaging results of event B

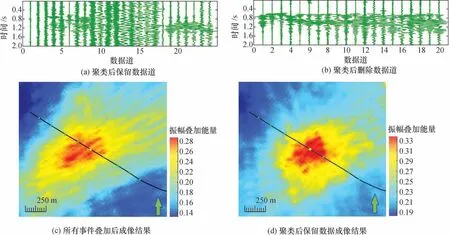
图11 事件C 成像结果对比Fig.11 Comparison of imaging results of event C

3 结 论

本文将统计学中的聚类分析方法在微地震成像中进行了应用,将每道信号看作一个样本,根据信号的特征进行分类,再通过各道相关性去除P波振幅较弱的数据道。

聚类算法在实际应用中计算效率高,识别较为准确,能够快速识别和提取距离相近的数据道,无需人工初至拾取进行微地震事件成像,适合于微地震监测实时定位处理。

筛选后的地震数据成像结果明显改善,且叠加的相似性值域明显增大,提高了定位的可靠度。

致 谢

感谢深听（北京） 科技有限责任公司DeepListen 解释软件，为本文提供了数据处理的基础。