单通道盲源分离在低轨星座系统间干扰减缓中的应用*

李 伟，潘 冀，严 康，魏文康，王 贺

(国家无线电监测中心，北京 100037)

0 引 言

近些年来，低轨通信星座系统凭借空地传播损耗小、传输时延低的优势，成为当前卫星通信领域的研究热点[1]。随着低轨星座系统爆发式发展以及卫星规模不断变大，世界各国对卫星频率资源的需求十分旺盛，资源缺口巨大。卫星频率资源的有限性导致不同低轨通信星座系统的频率集中使用，比如OneWeb、Starlink、Telesat、Kuiper等低轨星座系统都规划使用了Ka频段资源。另外，这些新兴低轨通信星座系统的卫星规模庞大，用户终端部署广泛，服务覆盖全球，卫星或地球站接收端不可避免地同时接收到多个同频信号，导致系统底噪抬升，接收性能下降。因此，研究适用于低轨通信星座系统间的干扰减缓方法尤为必要[2]。

针对卫星通信系统间同频干扰减缓问题，可从三个维度考虑：空间域、功率域和信号分割[3]。文献[4]提出了一种基于空间隔离的干扰减缓方法，通过设置对地静止轨道(Geostationary Satellite Orbit，GSO)卫星系统与低轨星座系统间的空间隔离角来减缓干扰。文献[5]提出了一种针对低轨星座系统与GSO系统下行同频干扰场景的自适应功率控制技术，通过适时改变低轨星座系统的发射功率来确保GSO系统受到的干扰功率水平低于门限值。文献[6]提出了一种渐进俯仰技术，通过调整卫星姿态以及发射功率来缓解OneWeb星座系统与GSO系统间的同频干扰，其本质上是一种基于空间域和功率域的干扰缓解技术。在信号分割方面，文献[7]提出了基于最大后验概率的方法来帮助低轨卫星接收端分离出GSO卫星信号，从而获得GSO系统的频谱使用状态，有针对性地保护GSO系统。上述研究主要针对低轨通信星座系统与GSO卫星系统之间同频干扰场景提出的干扰缓解方法。在低轨通信星座系统共存的场景下，低轨卫星之间、低轨卫星与地球站之间的相对位置、空间几何关系均是时变的，并且这些系统都采用多波束通信体制。因此，干扰链路时变动态特性更为复杂。上述研究对解决低轨通信星座系统之间同频干扰问题的借鉴意义不大。

低轨通信星座系统间的干扰减缓方法研究目前处于起步阶段，相关文献报道相对较少。从信号分割角度来看，盲源分离方法可以从混合信号中分离出有效信号。文献[8]提出了一种基于盲信号分离的机载甚高频数据广播接收机同频干扰抑制方法，对机载甚高频数据广播接收机接收到的期望信号与同频干扰信号进行分离达到抑制同频干扰的目的。文献[9]提出了一种分离脑电图信号的方法，通过奇异频谱分析(Singular Spectrum Analysis，SSA)与独立成分分析(Independent Component Analysis，ICA)将脑电图信号从单通道信号源中分离，并验证了此算法的有效性。文献[10]利用盲源分离算法对卫星图像进行噪声识别和消除，进而有效分析与大气相关的信息。针对低轨通信星座系统间的同频下行干扰问题，本文将深入研究盲源分离方法在在多低轨通信星座系统共存场景之中的应用，将有用信号从地球站接收到的混合信号中分离出来，得到所需期望信号，抑制同频干扰信号，从而提升系统频率兼容性，为未来多个非对地静止轨道(Non-Geostationary Satellite Orbit，NGSO)通信星座系统同频共存提供了一种思路和方法。

1 干扰模型

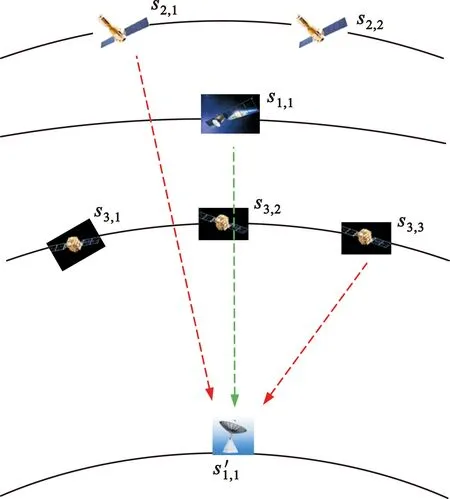
图1 低轨通信星座系统间下行干扰场景示意图

低轨通信星座系统地球站接收到的观测信号y(t)为受扰信号、干扰信号以及噪声三者的一维混合信号，表示如下:

y(t)=As(t)。

(1)

式中：s(t)=(s1(t),s2(t),…,sm(t))H为m个独立的信号源，其中s1(t)为低轨通信星座系统发射的有用信号，s2(t),…,sm-1(t)为其他多个低轨通信星座系统发射的干扰信号，sm(t)是噪声信号；A是一个1×m的系数矩阵，表示等效信道响应向量。已知各卫星发射的信号si(t)之间相互独立，本文研究目标是求出解混矩阵w，使得

x(t)=wy(t)。

(2)

式中：x(t)就是原始信号s(t)的估计；w是A的广义逆矩阵，它的行数代表独立信号源的个数，列数代表地球站观测到的信号个数。

2 基于单通道盲源分离的干扰减缓方法

在多个低轨通信星座系统同频共用的下行干扰场景中，受扰地球站接收到来自多个低轨卫星的干扰信号的来波方向较为分散，空地链路传播距离较长，天然形成空间隔离。地球站所处环境相对简单，其接收信号主要为直视信号，信号包络服从莱斯分布[11]。因此，受扰地球站接收到的干扰信号特征符合使用盲源分离算法的前提，源是相关独立的，且均为非高斯或者最多有一个高斯信号。针对同频下行干扰问题，利用单通道盲源分离算法从混合信号中将受扰信号提取出来[12]，从而实现多个低轨通信星座系统的频率共用共享。先通过奇异谱分析算法将地球站接收到的一维卫星信号转化为多维数据，再通过快速固定点算法将相互独立的卫星信号从地球站观测信号中分离开来。

2.1 奇异谱分析算法

奇异谱分析算法将单通道信号分解为不同成分的信号。该算法包括分解和重构两个基本步骤，每个步骤由两个子步骤组成。

(1)分解

包括矩阵嵌入和矩阵分解两步。在嵌入步骤中，将所接收到的一维时间序列信号y(t)=(y1,y2,…,yN)转化为M×L轨迹矩阵Y，其中y1，y2，…，yN表示每一时刻接收到的信号。

(3)

轨迹矩阵Y的行数M为自定义长度(不宜超过原始信号长度N的1/3)，列数L=N-M+1。嵌入步骤完成后，将Y分解为M个低秩矩阵，可用奇异值分解(Singular Value Decomposition，SVD)求出低秩矩阵。直接对M×L的矩阵进行奇异值分解涉及大量的运算，但可通过求解矩阵C=YYH的特征值和特征向量来计算观测矩阵Y的奇异值。用λ1,λ2,…,λM表示特征值，q1,q2,…,qM表示特征向量，将特征值按降序排序后对应M个特征向量，则观测矩阵Y中第j个分量的轨迹矩阵可表示为

(4)

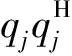
(2)重构

包括分组和对角平均两步。分组是为了将不同成分的信号分隔开。在信号处理领域，通常认为前面r个较大的奇异值能够反应信号的主要能量，即

(5)

最后，通过对角平均计算，将分组得到的各卫星轨迹矩阵转换成一维信号矩阵。

2.2 快速固定点算法

快速固定点算法又称FastICA算法，本质上是一种独立成分分析算法，也是一种优化算法。对经过奇异谱分析算法后得到的数据使用FastICA算法求解得到最终解混矩阵[13]。FastICA算法通过改变累积分布函数使得解混矩阵快速迭代，从而更快得出各卫星所发射的信号[14]。算法主要包括两部分，先对地球站观测信号矩阵进行零均值以及降低冗余性的处理，再进行解混矩阵的迭代求解。

2.2.1 预处理部分

(1)将数据按行去中心化，这样能简化ICA算法:

(6)

式中：X表示经过奇异谱分析后的重构信号，xj为重构信号X中的行向量，m为重构信号的列数，n为重构信号的行数。

(2)白化处理，即去相关性。通常来说，卫星所发射的信号都具有相关性，在信号矩阵中减去卫星发射信号的均值并对信号进行白化处理可将各卫星信号间的相关性去除，有利于解混矩阵的计算。此外，将卫星信号矩阵进行预处理与未对卫星信号矩阵进行处理相比，前一种做法有利于提高算法收敛性。求协方差矩阵：

(7)

特征分解：

CV=VΛ。

(8)

式中：V=[v1,v2,…,vn]是协方差矩阵C的特征列向量，Λ=diag(λ1,λ2,…,λn)是特征向量所对应的特征值矩阵。经过预处理后，混合信号矩阵变为

(9)

2.2.2 核心算法部分

估计分离矩阵w，具体过程如下：

首先引入一种定点迭代方法：

w=E{vg(wHv)}。

(10)

式中：g为累积分布函数的导数。在式(10)两端分别加上αw，得到式(11):

(1+α)w=E{vg(wHv)}+αw。

(11)

α值可通过拟牛顿法求解得到。按照库恩塔克(Kuhn-Tucker)条件，在E{(wHv)2}=‖w‖2=1约束下，E{vg(wHv)}的最优值可通过下式获得：

E{vg(wHv)}+βw=0 。

(12)

式中：β为常数。将式(12)左边项记为F，其雅可比矩阵为

J{F(w)}=E{vvHg′(wHv)}+βI。

(13)

式中：I为单位矩阵，g′为g函数导数。因为已经对地球站观测信号进行去均值和白化处理，则式(13)右边第一项可等效为

E{vvHg′(wHv)}≈E(vvH)E{g′(wHv)}=

E{g′(wHv)}I。

(14)

因此，得到w迭代公式如下：

w←w-[E{vg(wHv)}+βw]/[E{g′(wHv)}+β]。

(15)

对式(15)两边同时乘以E{g′(wHv)}+β即得到分离矩阵w：

w←E{vg(wHv)}-E{g′(wHv)}w。

(16)

完整的单通道盲源分离算法伪代码设计如下：

输入：源信号数量,地球站观测信号,奇异谱分析算法窗口长度。

输出：分离出的低轨卫星信号。

1 function SSA-ICA(Ns，Y，M)

2 ReadY//输入观测矩阵

3Y←Hankel(Y) //对观测矩阵进行分组

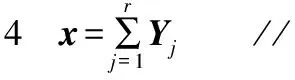
5x←x-mean(x) //矩阵零均值化

6v←Whiten(x) //白化处理

7g(y)←tanhy//g函数设置

8w←ones(N,1) //初始解混矩阵

9 fori←1 to 100 //算法迭代

10w←E{vg(wHv)}-E{g′(wHv)}·w

11 end

12s←w·v//分离矩阵

13 end function

2.3 分离结果的不确定性

利用单通道盲源分离算法虽可从混合信号中将有用信号和干扰信号分离开来，但无法直接甄别出有用信号和干扰信号，并且这些信号在幅值上与卫星发射信号可能存在差异，即通过所提算法得到的多个信号具有顺序和幅值的不确定性[15-16]。

由于卫星的发射信号以及无线信道特性都无法获知，因此卫星发射信号的幅值变化和等效信道响应向量对应系数的变化对地球站接收信号的影响是一样的，单通道盲源分离算法所估计得到的卫星发射信号的幅度并不是唯一的。

由于可能存在一个未知的矩阵p，使得经过变化的卫星发射信号矩阵ps与原本的卫星发射信号矩阵s在顺序上发生了一些改变，但仍然满足

x=Ap-1ps。

(17)

此时可将卫星发射信号看作是ps，信道响应向量看作是Ap-1。因此，通过单通道盲源分离算法求得的卫星发射信号矩阵并不会按照某种固定的顺序进行排序，即卫星信号的混合顺序存在多种可能性。然而，从分离卫星发射信号的角度来看，允许存在这种顺序的不确定性。

2.4 单通道盲源分离算法的评价标准

利用相关系数R[17]和均方根误差(Root Mean Square Error,RMSE)[18]可以确定分离信号与源信号之间的对应关系并评估单通道盲源分离算法的有效性。相关系数R表达式如(18)所示：

(18)

式中：X代表受扰低轨卫星的发射信号矩阵，Y代表从混合信号中分离出来的受扰信号矩阵，N为信号的采取的样本数。相关系数R的取值范围为0≤|R|≤1，当|R|≥0.8时，即可说明分离卫星信号与原始卫星信号高度相似。

均方根误差RMSE表达式如(19)所示：

(19)

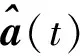
相关系数R能够有效反映卫星发射信号波形间的相似度，且允许卫星信号间幅度不一定相同，这对于存在幅度不确定性的盲源分离算法尤其适用。均方根误差RMSE能够衡量分离NGSO信号与原始NGSO信号之间的误差大小。因此，通过计算所提算法分离出的信号与卫星原始发射信号之间的相关系数以及均方根误差，就可以评价所提算法在多大程度上能有效分离得到受扰信号和干扰信号[13,16]，进而评估基于单通道盲源分离的低轨星座系统间干扰缓解方法的有效性。

3 建模与仿真

选取典型低轨通信星座系统作为仿真对象以获得一般性结论。考虑到当前低轨通信星座系统规划使用的频率主要为Ka频段，本文以Ka频段的OneWeb星座系统作为受扰系统，以Starlink星座系统作为施扰系统进行仿真分析。

OneWeb星座系统由720颗低轨卫星组成，有18个轨道面，每个轨道面40颗卫星，轨道高度为1 200 km，倾角87.9°。经查ITU卫星网络资料数据库，OneWeb星座系统卫星网络资料ID为113520120，选取下行波束GTB的参数信息作为OneWeb星座系统的仿真参数配置。Starlink星座系统由4 409颗低轨卫星组成，有18个轨道面，每个轨道面40颗卫星，轨道高度分布在550～1 325 km之间，倾角分布在53°～74°之间。经查ITU卫星网络资料数据库，Starlink星座系统卫星网络资料ID为114520273，选取下行波束DA2831的参数信息作为Starlink星座系统的仿真参数配置。具体的系统仿真数据如表1所示[1,19-20]。

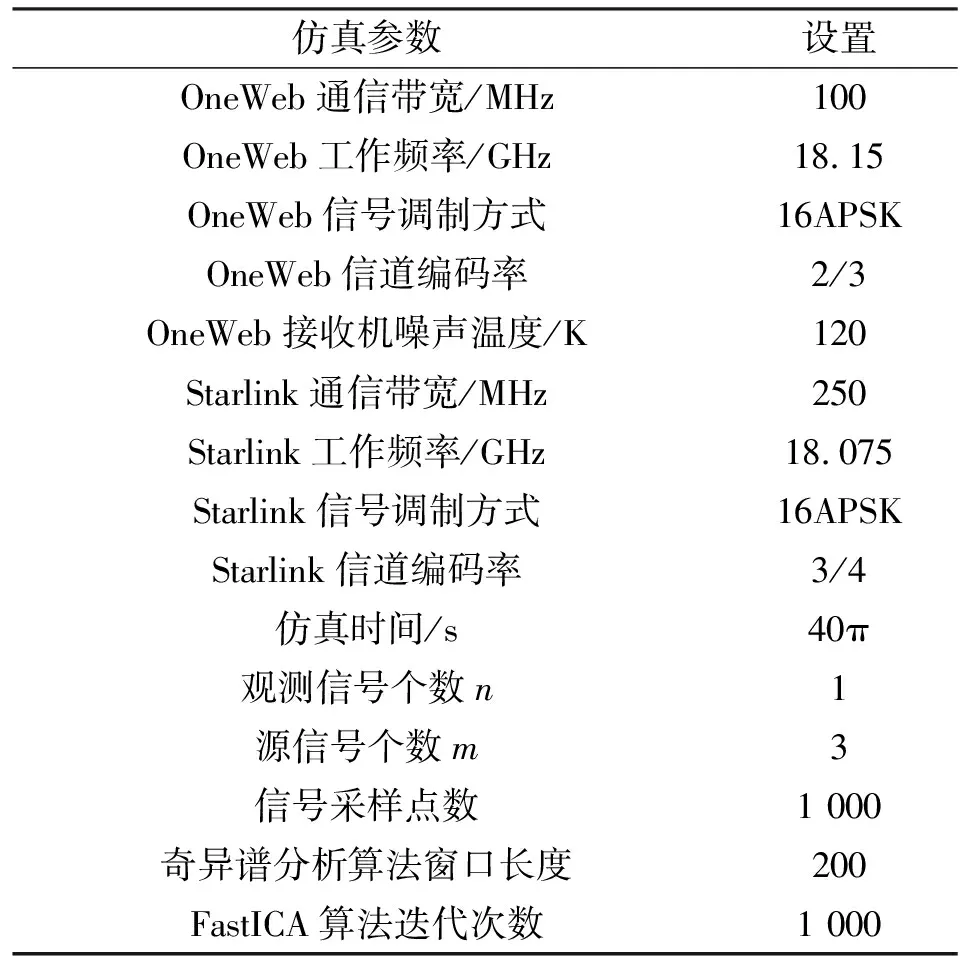
表1 系统仿真参数

图2为原始的OneWeb信号和Starlink信号，图3为采用基于单通道盲源分离的干扰减缓方法后分离得到的OneWeb信号和Starlink信号。对比图2和图3可知，即使存在高斯白噪声，所提算法能从混合信号中，提取得到受扰信号，并对受扰信号波形进行很好地还原。由于低轨卫星通信系统的通信体制、信道带宽划分和载频都不一样，通过盲源分离后得到的信号，OneWeb地球站可根据载频信息获取目标信号。

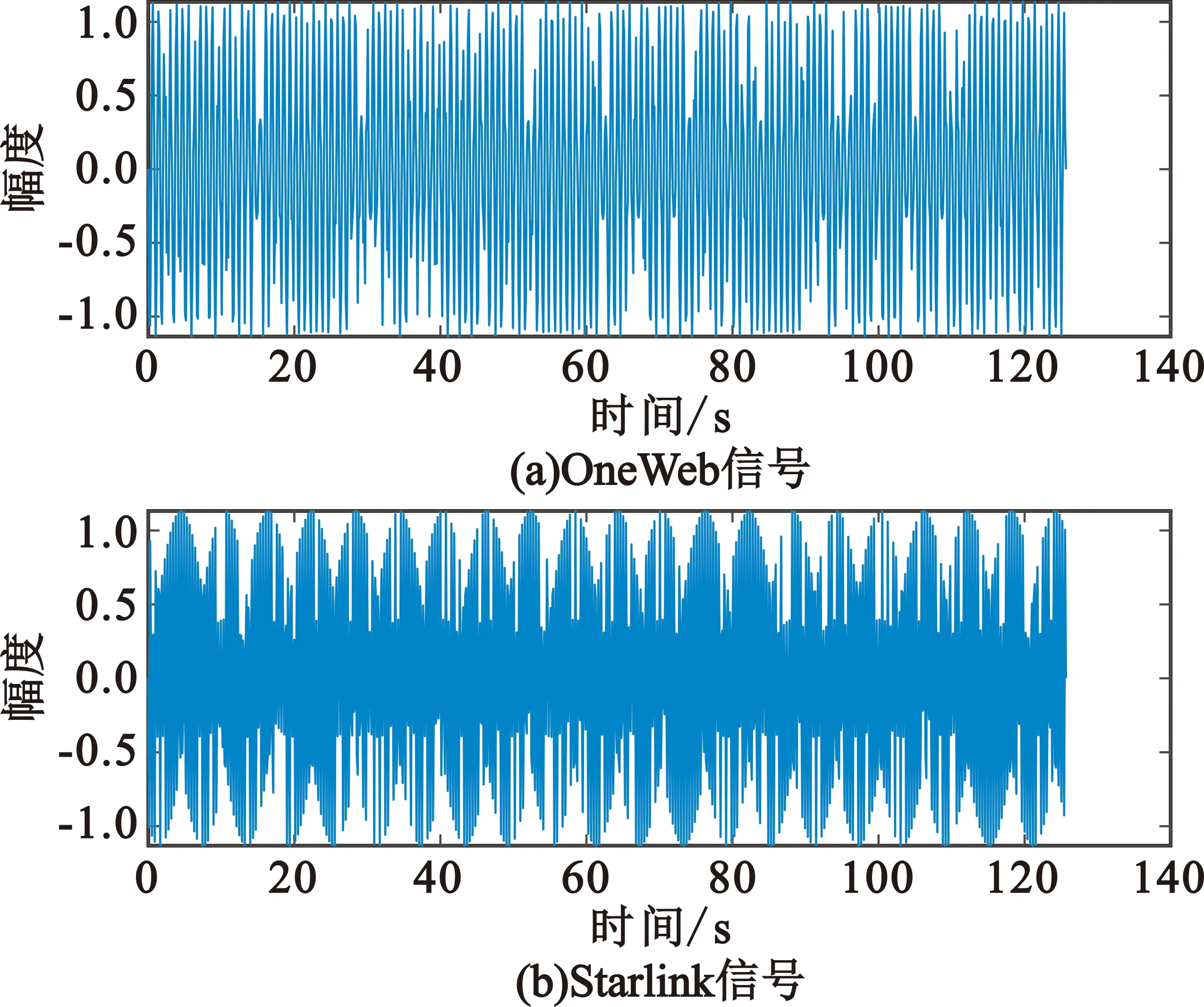
图2 混合前的原始卫星信号

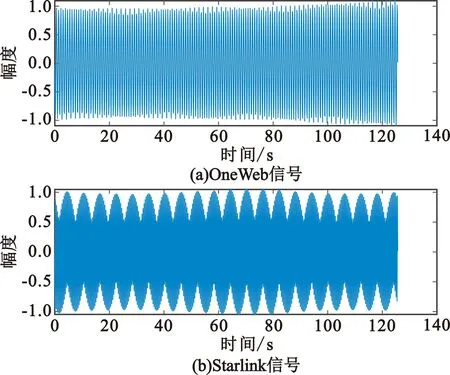
图3 分离后的卫星信号

表2给出了原始OneWeb信号和分离后的OneWeb信号的相关系数和均方根误差的计算结果。由表2可知，相关系数都在0.8以上，均方根误差普遍分布在30%～50%之间，从这两个评价指标反映出所提方法能从混合的OneWeb信号、Starlink信号和高斯白噪声之中基本恢复原始OneWeb信号，进而有效减缓OneWeb星座系统和Starlink星座系统之间的同频干扰。

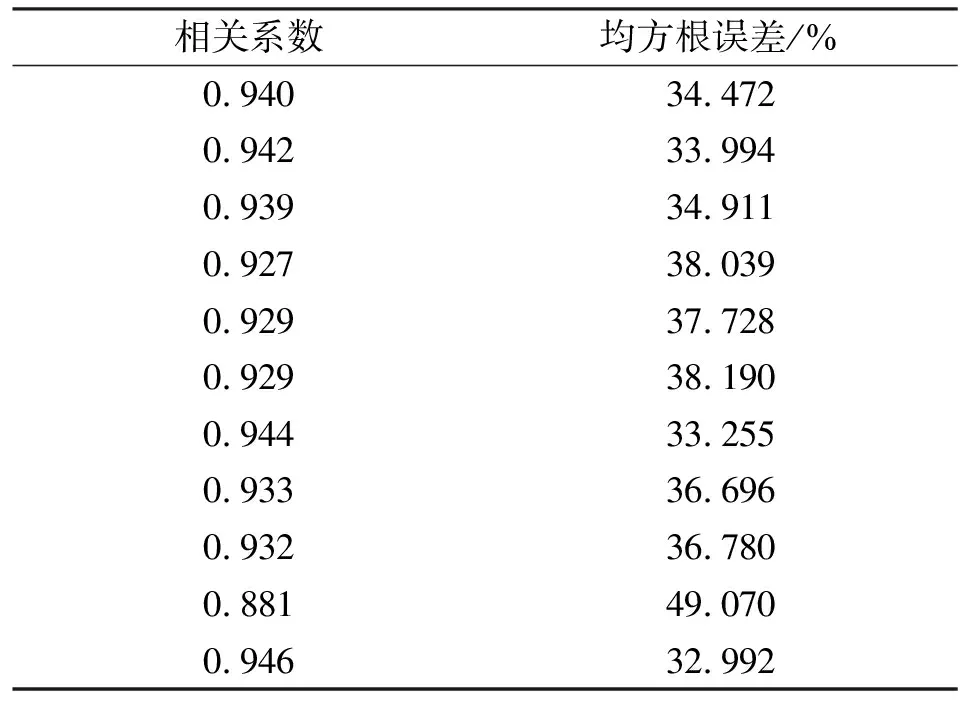
表2 仿真结果比较

4 结束语

本文针对多个低轨通信星座系统间的同频干扰问题，从信号维度对下行干扰场景进行数学建模，提出了基于单通道盲源分离的干扰减缓方法。该方法应用了单通道盲源分离算法，将观测矩阵转换为对应的轨迹矩阵，提取信号中主要成分，再利用FastICA算法将干扰信号和受扰信号分离。选取OneWeb星座系统作为受扰方，Starlink星座系统作为施扰方，以相关系数和均方根误差作为评价指标，仿真分析了OneWeb信号分离前后的相似程度，多组数据的相关系数皆在0.8以上，均方根误差普遍低于50%，表明该方法能够从混合信号之中有效分离出有用卫星信号，从而印证了基于单通道盲源分离的干扰减缓方法能够极大减缓低轨通信星座系统间干扰，提升系统间的频率兼容性。上述研究有望为低轨通信星座系统的干扰管理设计以及频率国际协调提供参考。下一步将重点考虑多普勒频移对盲源分离算法应用的影响。