基于起作用集法的地层组分分析方法

王黎明,由立志,王慧,缑艳红,刘芳,项艳

(1.中国石油集团测井有限公司大庆分公司,黑龙江大庆163000;2.中国石油集团测井有限公司测井地质研究院,陕西西安710077;3.中国石油集团测井有限公司制造公司,陕西西安710077)

0 引 言

中国20世纪90年代引入斯伦贝谢公司的ELAN_PLUS软件,一直将其作为探井、评价井常规测井资料处理解释的主要软件。该软件可以对储层进行准确合理的定量解释并得到符合地质规律的地层组分[1-2]及相应的孔隙度、渗透率和饱和度,取得了良好的应用效果。但该软件并未公开算法,不能进行有效的二次开发,并且存在数据加载操作繁琐等问题,增加了解释人员的处理工作量。

在ELAN_PLUS软件提出的地层是由冲洗带、原状地层组成的梯级侵入剖面等假设的基础上,建立了地层组分求解模型、常规测井仪器响应方程,并通过最优化起作用集法求解方程目标函数的最优解,求取的地层组分与ELAN_PLUS软件及岩心分析结果基本一致。

1 地层组分求解模型及响应方程建立

1.1 地层组分求解模型

储层是由黏土、矿物骨架、流体组成,常规测井资料最优化处理方法通过仪器测量值与地层组分的关系建立求解模型,定量求取这些地层组分的体积百分含量[3]。

ELAN_PLUS软件假设地层是由冲洗带、原状地层组成的梯级侵入剖面。在冲洗带和原状地层,所有固态组分数值相等,其他流体组分总和相等,可以用侵入因子(FI)表示仪器测量值受冲洗带的影响程度,用(1-FI)表示其受原状地层的影响程度。

1.2 响应方程

响应方程是仪器测量值随组分变化而变化的数学描述,主要包括线性方程、非线性方程、等式约束、不等式约束。线性方程包括密度、中子、声波时差、自然伽马等测井响应方程。以密度测井为例,其响应方程为

(1)

式中,RHOB为密度测量值,g/cm3;ns为固态组分数目,个;nx,f为冲洗带流体组分数目,个;nu,f为原状地层流体组分数目,个;ρi、ρj、ρk为第i、j、k种组分密度响应值,g/cm3;Vi、Vj、Vk为第i、j、k种组分体积含量,%;FI,RHOB为密度侵入因子,无量纲。

非线性方程包括深电阻率、浅电阻率、自然电位等测井响应方程。以深电阻率测井常用的印度尼西亚方程为例

(2)

式中,Ct为测量电导率值,S/m;Cu,c为黏土电导率,S/m;Vc为黏土体积含量,小数;ev,c、mv,c为饱和度方程中与黏土体积含量相关指数,无量纲;Cu,w为原状地层水电导率,S/m;φ为孔隙度,小数;a为阿尔奇公式岩性系数,无量纲;m为胶结指数,无量纲;n为饱和度指数,无量纲;SW为含水饱和度,小数。

如果模型中有1个或多个非线性方程,模型求解就要采用非线性算法。非线性算法会使方程组的求解迭代次数增多且极易陷入局部极小值。该研究在求解方程组时将地层组分初始值带入SW的求解公式中,将电阻率方程由非线性方程转化为线性方程。深电阻率测井的线性方程为

(3)

式中,nu,w原状地层水组分数目。非线性方程转为线性方程后,方程组变为线性方程组,方程组求解为凸规划问题,可以快速收敛且得到全局最优解[4]。

等式约束主要为:冲洗带流体组分体积含量之和等于原状地层流体组分体积含量之和,所有组分(流体组分只选冲洗带流体组分)体积含量之和为1等。不等式约束主要为限制组分的体积含量,常用的不等式约束有孔隙度约束、残余水约束、电导率约束等。

由以上方程和约束可以得到需要求解的方程组

(4)

式中,xi为第i种组分的体积含量,%;Ai,j为第i种组分对第j种仪器的响应值;Bj为第j种仪器的测井值。为了充分利用测井信息,提高测井解释的可靠性,一般情况下m>n,此时方程组为超定方程组,有1个最优解。由最优化理论可以建立测井最优化目标函数

(5)

式中,Uj为第j种仪器测井值的不确定性值,无量纲,值由仪器的不确定性和模型的不确定性组成;Wj为第j种仪器测井值的权系数,无量纲,质量差的测井曲线赋予低权系数,质量好的测井曲线赋予高权系数[5]。

2 求解算法

由于式(5)带有约束,无法使用解超定方程组最常用的最小二乘法[6],该研究选择最优化二次规划算法中的起作用集算法来求解方程组,得到最优解。

对于存在不等式约束的二次规划,在每次迭代中,以已知的可行点为起点,把在该点起作用的约束作为等式约束,将不起作用约束去掉,在此等式约束下极小化目标函数,求得新的可行点以后,重复以上做法。通过解一系列等式约束的二次规划,实现不等式约束的优化称之为起作用集方法。式(5)可以转化为具有不等式约束的二次规划问题标准形式

(6)

式中,H为n阶矩阵;q为n维列向量;C为m×n矩阵;b为m维列向量;r为常量;Aeq为l×n矩阵;Beq为l维列向量;r为等式约束个数。

运用起作用集法,选取可行点x(0)作为求解初始点,地层第1个处理点求解初始点的选取原则是所有组分等分,以后每个处理点选取上一个处理点的最优解作为初始点。以x(0)为起点,把在该点起作用约束作为等式约束,在此约束下极小化目标函数f(x),而其余的约束暂时忽略,求得新的可行点后,再重复以上做法。设在第k次迭代中,已知可行点x(k),在该点起作用约束指标集用I(k)表示,就转化为求解等式约束问题。

(7)

式中,Ci是矩阵C的第i行,也是在x(k)处起作用的约束函数的梯度。令δ=x-x(k),则

(8)

于是问题变成了δ的二次规划问题

(9)

式(9)可用拉格朗日方法求解,具体方法见参考文献[7]。求出最优解δ(k),然后根据不同情况继续求解。如果δ(k)=0,则x(k)为式(7)的最优解,这时应判断x(k)是否为式(6)的最优解,即能否满足其他约束。如果满足,由于式(6)是凸规划,则x(k)即为全局最优解;如果不满足,则继续其他约束重复求解。如果[x(k)+δ(k)]是可行点,但δ(k)≠0,则继续此约束的下一次迭代;如果不是可行点,则沿着δ(k)方向以α的步长继续搜索,直到[x(k)+αδ(k)]为可行点,然后逐步判断直到x(k)成为全局最优解。

因为解方程组时将电阻率非线性方程线性化,此时需要将最优解x重新作为方程组初始点,以此初始点将非线性方程再次转化为线性方程,再次用起作用集方法得到新的最优解。重复以上过程直到当前深度最优解不再变化。整个求解过程见图1。

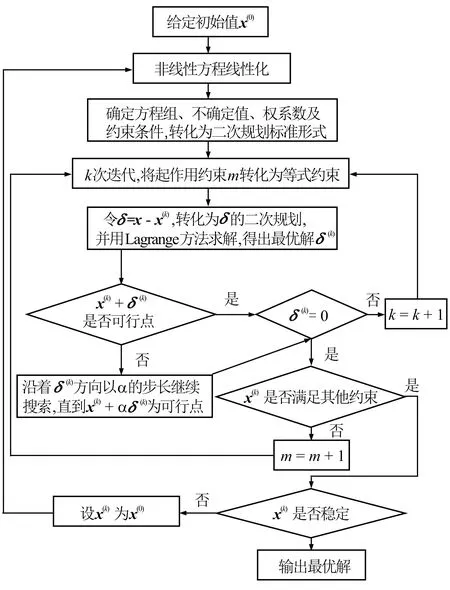
图1 地层组分起作用集方法求解流程图

3 实际测井资料处理

综合上述模型、响应方程建立及最优化起作用集求解方法,建立了一套完整的测井最优化处理方法,基于LEAD4.0平台开发了完整的处理软件,用户可以根据实际情况选择线性算法和非线性算法。利用软件对实际测井资料进行处理,程序运算速度快,处理结果与ELAN_PLUS软件基本一致。截至目前处理了大杨树盆地、塔里木盆地、准噶尔盆地的砂砾岩、碳酸盐岩和火成岩生产井136口,应用效果良好。

杨×井在实际生产中用ELAN_PLUS软件处理解释,处理井段为甘河组、九峰山组地层。依据地区规律并结合该井实际情况以及录井资料,测井处理解释模型选用岩石模型,岩石选择砂岩、泥岩、煤、火成岩,火成岩岩性为玄武岩、安山岩、高阻凝灰岩、低阻凝灰岩,流体选择油和水。具体地层组分模型见表1,地层组分测井响应值见表2。

表1 杨×井选用的地层组分模型

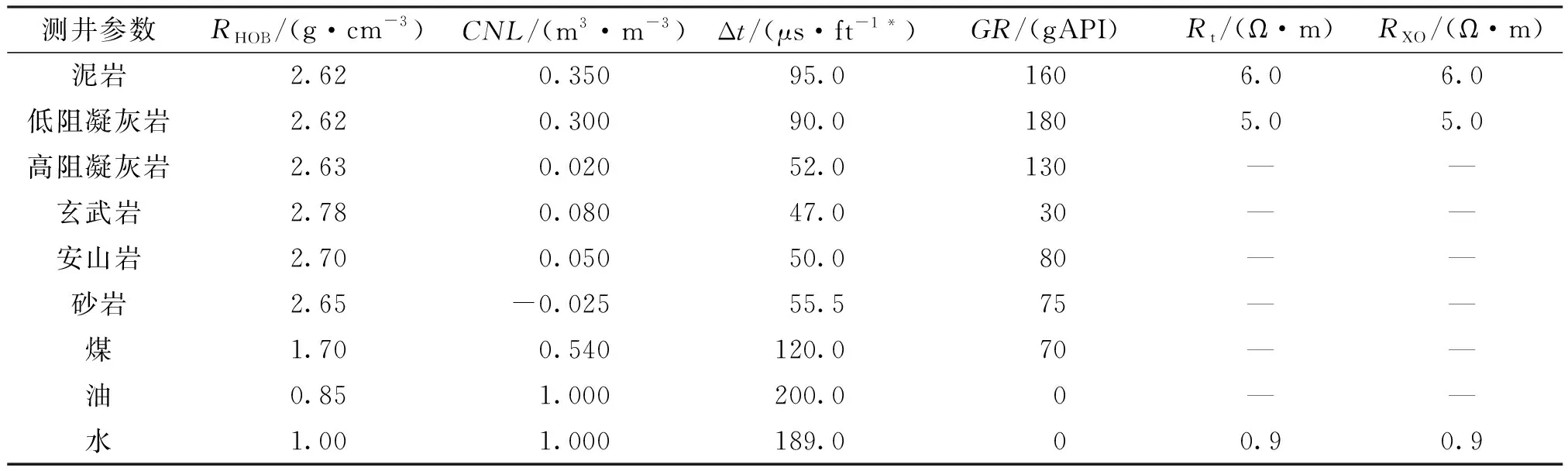
表2 杨×井地层组分测井响应参数

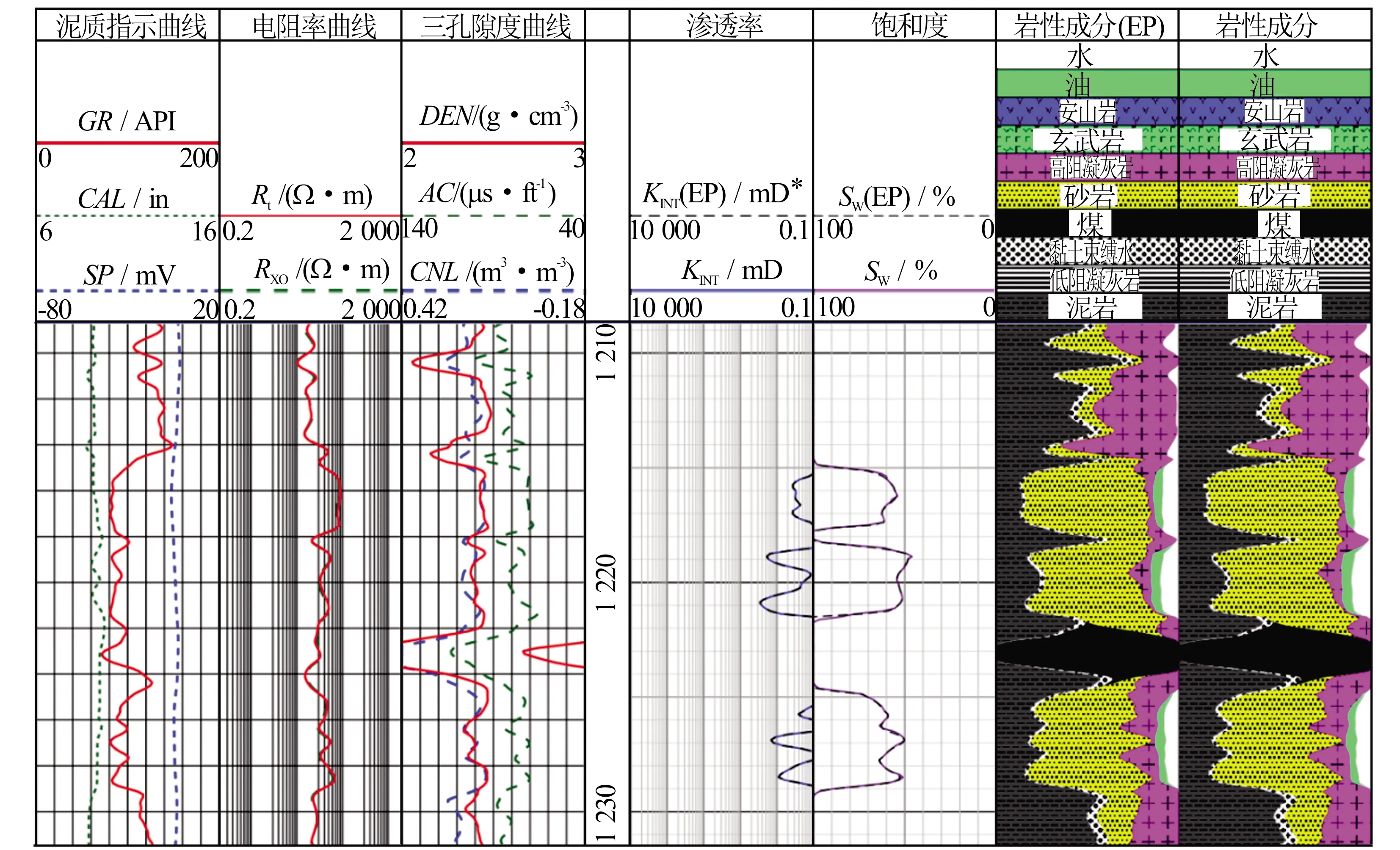
图2 杨×井处理结果与ELAN_PLUS软件处理结果对比注:带有EP标识的是ELAN_PLUS软件处理结果*非法定计量单位,1 ft=12 in=0.304 8 m,1 mD=9.87×10-4 μm2,下同

选取该井测试时提出的最优化处理解释方法,与ELAN_PLUS软件处理结果对比(见图2),各地层组分与ELAN_PLUS软件处理结果平均相对误差见表3。由图2和表3可以看出处理结果非常接近。

表3 杨×井地层组分本文方法与ELAN_PLUS软件处理结果对比

注:原状地层和冲洗带流体一起统计平均相对误差。

图3为城×井利用该文提出的方法得到的地层矿物组分含量与岩心分析结果对比图,第5道VCal和第6道VDol分别为最优化方法求得的灰岩含量和白云岩含量,横线加圆点符号表示相应的岩心分析结果,从图3中可以看出两者基本吻合。

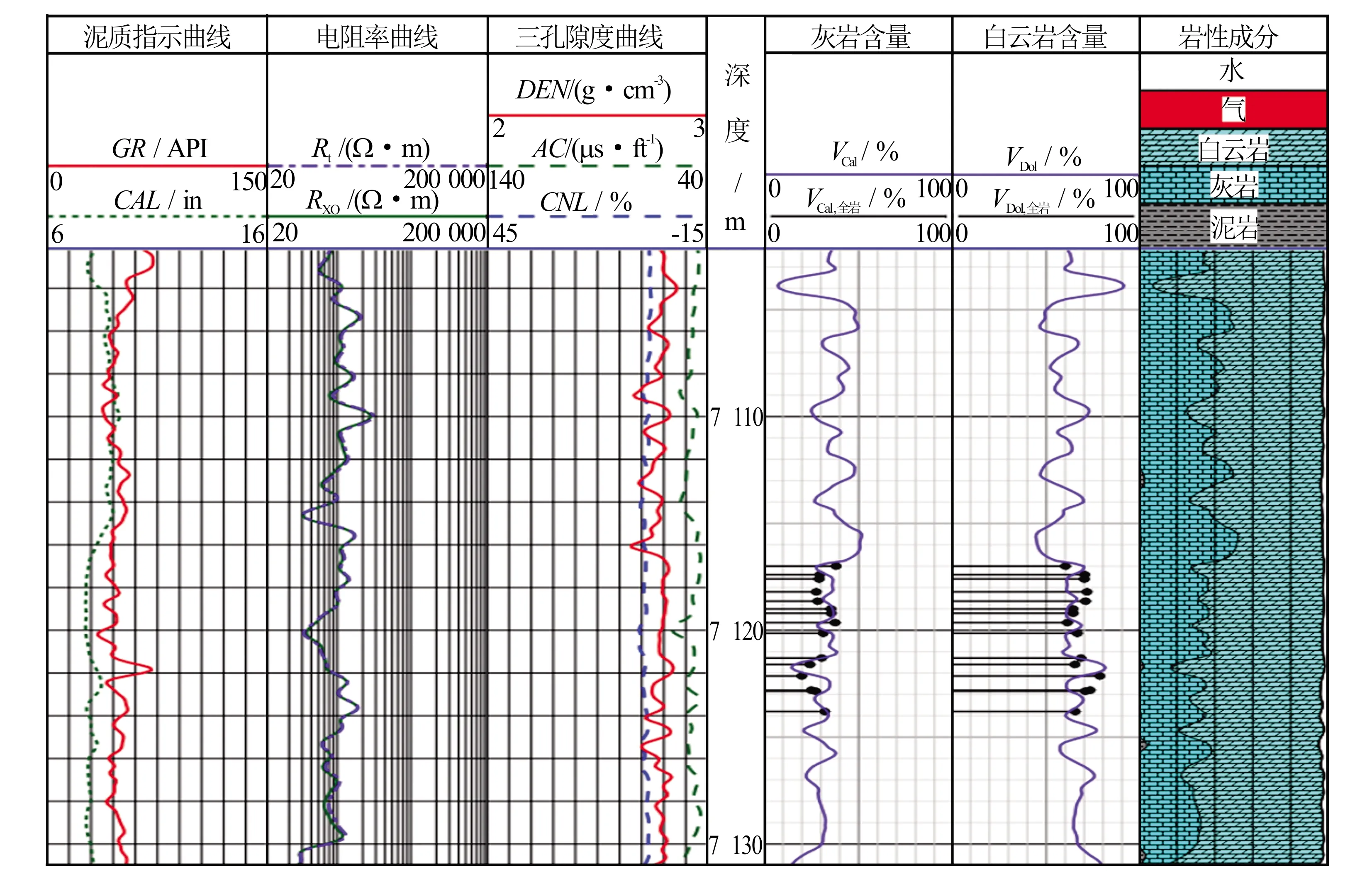
图3 城×井处理结果与岩心分析结果对比

4 结 论

(1)建立地层组分求解模型、响应方程,提出将非线性方程转化为线性方程,用最优化起作用集法求解带多个约束的线性方程组,形成了一套完整的常规测井资料最优化处理方法。基于LEAD4.0平台开发了完整的处理软件,解决了ELAN_PLUS软件无法二次开发、数据加载过程繁琐等问题。

(2)利用该方法对实际测井资料进行处理,与ELAN_PLUS软件处理结果对比,显示平均相对误差较低,与岩心分析结果基本吻合,验证了该方法的可靠性。

(3)应用基于该方法开发的软件,处理了大杨树盆地、塔里木盆地、准噶尔盆地的砂砾岩、碳酸盐岩、火成岩生产井,应用效果良好,下一步可对算法及软件进行完善,拓宽其应用范围。