基于轨迹平滑的GM-PHD跟踪算法

李鹏 张骏男 陈澄 赵琦 王文慧

江苏理工学院 计算机工程学院 江苏 常州 213001

引言

多目标跟踪旨在存在杂波干扰和漏检的复杂环境下，对数量未知的目标进行跟踪并有效估计其状态，目前以应用于导航、定位、无人驾驶等多个前沿领域。

随机有限集（RFS）理论最早由Mahler提出，是目前目标跟踪领域较为经典的数学模型。该理论用数学模型描述了量测产生的过程，认为量测在空间分布上服从某个特定分布，只要对目标的状态空间进行求解就可以得到目标的状态信息。基于该理论的主要数学框架包括PHD[1]和CPHD[3]等，给出了求解目标状态空间的数学形式，但由于该数学形式很难直接求解，因此无法应用于实际。为了将数学框架付诸应用，Vo等人提出了GM-PHD[2]跟踪算法，用高斯混合方法拟合状态空间的复杂分布，可以用较小的计算代价获得较好的跟踪结果。算法假设每个目标每帧最多产生一个量测，每个目标的量测相互独立，量测在空间上服从高斯分布。对每个量测进行多假设跟踪，根据高斯分布计算假设权重，则可根据权重删减、提取目标状态，得到最终跟踪结果。然而，目标紧邻时多个目标的量测彼此靠近，导致算法难以正确地估计目标真实状态，使跟踪效果明显下降，是多目标跟踪领域的难点。

针对以上问题，提出一种改进的GM-PHD跟踪算法。首先，基于高斯分量标签技术[4]对GM-PHD进行轨迹关联，对每个高斯分量添加一个独立标签，标签随跟踪过程不断更新，最终生成每个目标的航行轨迹。然后，对每条轨迹进行平滑[5]，充分考虑目标漏检、杂波等复杂环境，设计一套适用于多目标跟踪的轨迹平滑方法。实验结果表明，提出方法可以明显提高GM-PHD的整体跟踪精度。

2 GM-PHD跟踪算法

GM-PHD基于贝叶斯滤波技术，可在漏检、杂波等复杂环境下，对数量未知的目标实现实时跟踪。状态平滑是一种轨迹处理技术，主要用来对已估计的目标状态进行平滑处理，降低复杂环境对状态估计精度的影响，有效提高跟踪精度，是一种非实时的数据处理技术。目前，状态平滑相关基于以应用于单目标跟踪当中，但由于多目标跟踪的复杂性，状态平滑仍存在一定的问题。GM-PHD跟踪算法在状态平滑方面主要面对以下挑战：

（1）GM-PHD算法估计的目标状态是无序的，而状态平滑需要稳定轨迹进行数据关联，因此状态平滑技术无法直接应用于GM-PHD算法。

（2）由于多目标跟踪场景的复杂性，杂波、漏检等问题会影响状态平滑技术的应用。

针对以上问题，本文使用标签技术使GM-PHD生成有序的轨迹，并且考虑了漏检等复杂情况，使用滑技术来跟踪精度。

根据GM-PHD算法，首先对目标先验状态进行预测，先验概率定义为：

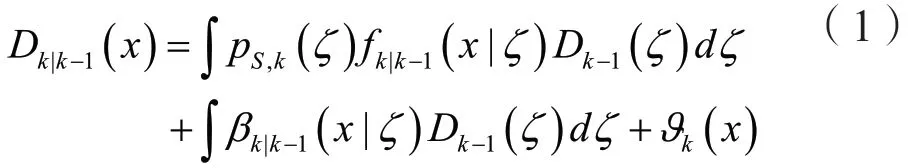
高斯混合后得：

其中：

其中：pS,k表示存活概率，表示权重，和分别表示先验运动状态和误差矩阵，Fk−1表示状态转移矩阵，Qk−1表示过程噪声矩阵。在观测到新一帧量测信息后，估算目标后验状态：

进行高斯混合后得：

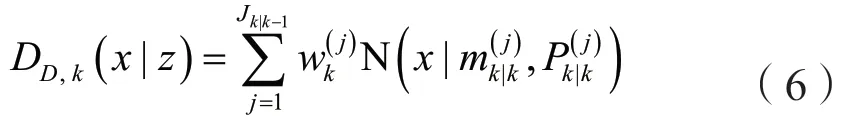
其中：

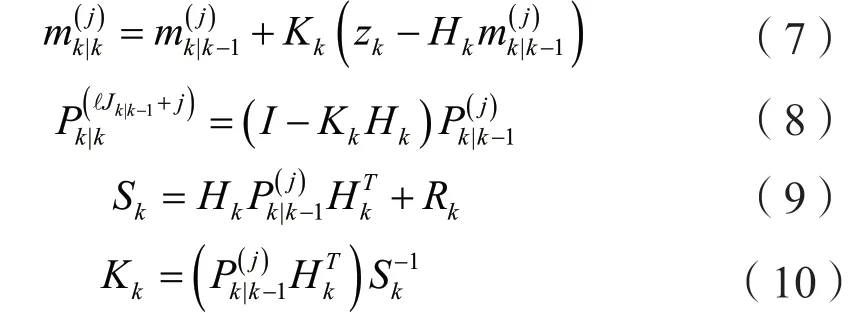
其中：Hk表示观测矩阵，kR表示量测噪声。权重可如下计算：

其中：pD,k表示检测概率，κk(z)是杂波概率密度。

3 改进的GM-PHD跟踪算法

平滑技术主要指根据多个帧所估计的状态进行进一步处理，得到更加平滑的状态，可有效避免目标紧邻时对跟踪精度造成的干扰。由于RFS理论的跟踪结果中不包含目标轨迹信息，因此将状态平滑技术应用于GM-PHD首先要估计的结果建立轨迹。这里使用标签法给每个高斯分量打上标签，通过整合标签即可获取目标完整轨迹，打标签的详细方法已在文献中给出[4]，即：

3.1 预测

3.1.1 对每个分量分配预测标签

3.1.2 给新生粒子分配标签

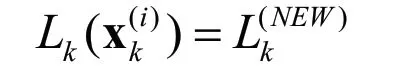
3.2 更新

每个由预测分量产生的后验分量继承预测分量的标签。

3.3 删减合并

若分量被删减，则对应标签被删减。

若多个不同标签的分量合并，则取权重最大的分量的对应标签作为最终标签。

若合并后有多个分量的标签相同，则权重最大的分量继承此标签，其他分量打上新的标签。基于标签技术，GM-PHD算法在跟踪中会根据标签生成每个目标的轨迹，这些轨迹中可能包含漏检等特殊情况，因此在进行平滑时需要进行特殊化处理，以此来保证多目标跟踪的有效性。设第i条轨迹所对应的目标的位置轨迹和误差矩阵为，其中tB和tD表示目标出生和死亡的时刻。基于目标状态的平滑方法[5]，令初始状态表示为：

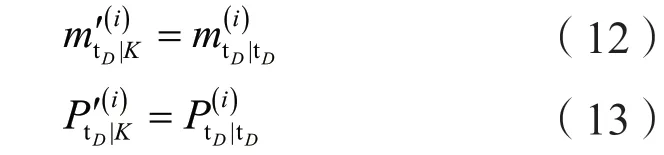
若轨迹在k时刻不为空，则：

若第k帧目标轨迹为空，则：

4 仿真实验

为验证提出方法的效果，进行了100次蒙特卡洛实验。场景中量测噪声的协方差矩阵为：，过程噪声协方差矩阵为。每帧产生量测的泊松均值为λk=20，目标检测概率为PD=0.99。场景设置了四个目标新生点位，每个点位的新生目标运动初始状态均为m0=[x0,0, y0,0]T，对应的误差矩阵为，初始权重均设置为0.01。

实验采用OSPA[6]来评价跟踪结果。图1是展示了100次仿真实验的OSPA误差结果，可见提出方法可有效提高原算法精度，降低OSPA误差。这一结果说明提出算法与平滑方法相结合，平滑后估计的轨迹更接近于目标真实轨迹，可有效降低杂波和紧邻造成的精度干扰。

图2是GM-PHD算法与提出算法的时间代价结果，可见提出算法与GM-PHD算法相比，在精度提高的同时略微提高了时间代价，因此更适用于对精度要求大于时间代价要求的跟踪系统。

（图1、图2见文末）

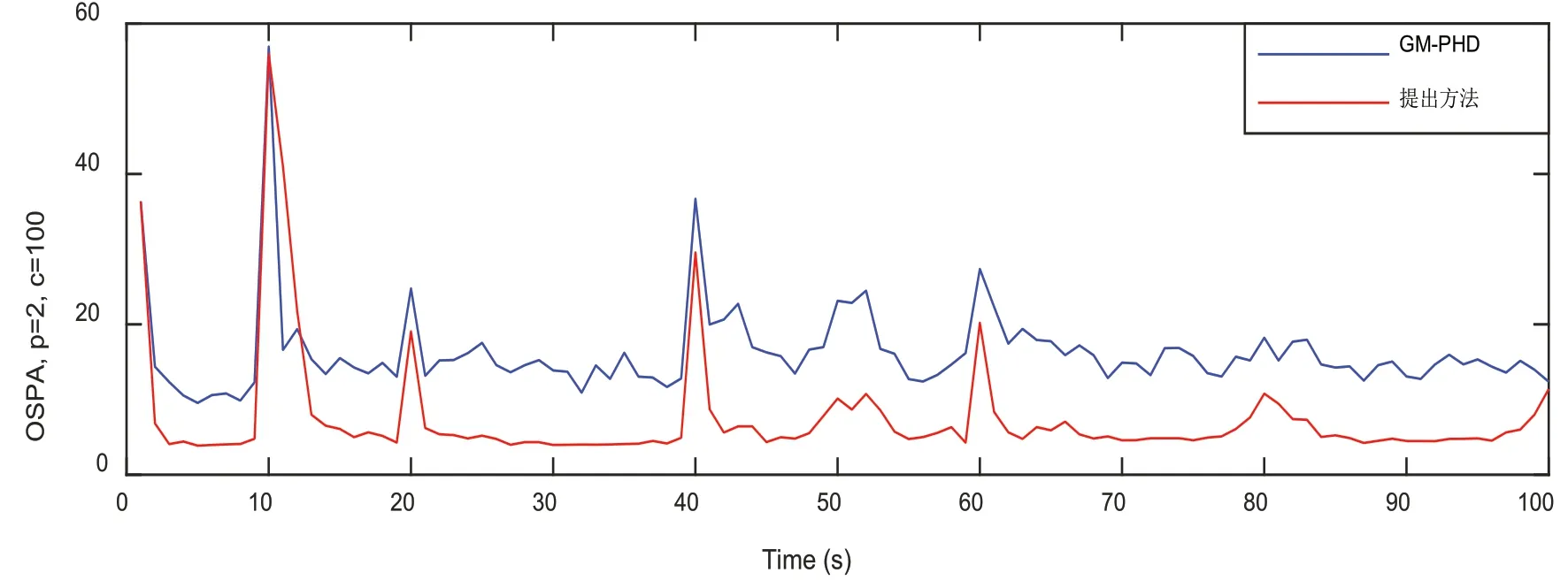
图1 100次实验的平均OSPA误差距离结果

图2 100次实验的平均时间代价结果

5 结论

本文对一种基于轨迹平滑的改进GM-PHD跟踪算法。仿真结果表明，提出方法可以较小的时间代价增长来大幅提高跟踪效果，使精度高度原算法。然而，需要指出的是，本文中平滑算法不能平滑当前时刻的GM-PHD状态估计结果，即不是一种完全实时的跟踪方法。因此，提出方法不适用于实时性要求较高的系统，适用于较高精度要求的系统。