磁体与运动导体相互作用的实验研究

翦知渐，谢 中，周艳明

(湖南大学 物理与微电子科学学院 大学物理实验中心，湖南 长沙 410082)

相对运动的非磁性导体与永磁体(或其他磁场)之间因电磁感应存在相互作用，研究这种相互作用对了解感应电机的运行、磁悬浮、涡流制动、磁感应探伤以及卫星在地磁场中的运动等具有重要作用[1-5]. 在这类体系中，电磁相互作用导致的磁体与导体之间的磁悬浮力和磁阻尼力是实际应用问题的焦点.

对于相对运动的导体与磁体之间的相互作用，理论上可以用麦克斯韦方程组和洛伦兹力来解决，但除了少数高对称性的情形外，一般很难得到解析解，所以实际应用中多采用模拟或数值计算的方法[6-7]. 另外，采用实验方法进行研究也较为有效[8-9].

本文介绍了研究磁体与运动导体之间相互作用的实验方法及相关的实验装置：位于永磁铁下方旋转的铝圆柱体内，因电磁感应产生涡流，涡流产生的磁场使磁体受到力的作用，通过测量相互作用力，可以对导体内的涡流及其产生磁场的特点进行分析. 该实验过程涉及许多电磁学的概念和定律，适合作为本科生的提高型或进阶型实验项目.

1 基本模型及测量结果

当磁体与导体之间有相对运动时，导体内的电子受洛伦兹力的作用产生运动，从而形成涡旋状的感应电流，电流的大小和分布与导体的电导率及形状有关，如图1所示. 磁体产生的磁场B0向下，下方的平板导体向左运动，导体内将会产生涡旋状的感应电流，其分布及产生的磁场BI大致如图1所示. 值得注意的是，左半部的感应磁场与外场方向一致，总磁场加强；右半部的感应磁场与外场方向相反，总磁场减弱. 涡旋电流的大小和总磁场的大小有关，因此涡旋电流的分布在磁场区域的左右两侧是不对称的.

图1 磁体与运动导体之间的电磁感应

对于不同形状、不同运动轨迹的导体，要给出涡旋电流的分布及其与外场相互作用的解析解是很困难的，只有少数高对称性的系统才能获得解析解[10-11]. 所以本文用实验方法对此进行研究，通过分析测量结果来解释相互作用过程，并对测量结果的特征给出定性及半定量的解释.

在实际应用中，人们最关心的是相对运动导致磁体所受水平方向的拽力(即导体所受的阻尼力)以及竖直方向的升力(磁悬浮力)，故设计了准确测量拽力和升力的实验装置. 由于在实验室内较难实现导体稳定的平动，所以本文用旋转代替平动，设计的实验装置如图2所示. 位于上方的是1个安装在特制悬臂梁上的长方形永磁铁，可近似认为其磁感应强度在长方形区域内是均匀的，大小为B0，方向朝下；下方是绕中心轴旋转的铝圆柱体，旋转角速度为ω. 旋转的铝圆柱体内会产生涡旋电场，涡旋电场产生感应磁场，感应磁场与原有磁场之间的相互作用导致磁体受到作用力，从而运动导体内及导体外的电场和磁场都会重新分布.

图2 实验装置示意图

利用电机驱动铝圆柱体旋转并控制其转速ω，悬臂梁上安装2个正交的力传感器，测量磁体所受水平方向的拽力FD及磁体所受垂直方向的升力FL(磁悬浮力)，测量结果如图3所示.从图中可以看到，随着转速ω的增加，水平方向的拽力FD和垂直方向的升力FL的变化不一致.随着转速ω的增加，FD的增速逐渐减缓，达到一定大小后基本保持不变；FL在较大速度区间内基本上单调递增.

图3 磁体所受拽力FD,升力FL与角速度ω的关系

2 对测量结果的解释

2.1 利用迭代过程导出感应磁场的表达式

导体内的涡旋电流及其产生的磁场满足麦克斯韦方程组：

(1)

其中最后1个方程是考虑洛伦兹力之后的欧姆定律.如果圆柱导体的旋转速度稳定，涡旋电流及其产生的磁场与时间无关，但对于非对称的边界条件，从方程组较难直接求解感应电流.本文用迭代过程来取代对联立方程组的求解：外磁场中的导体快速旋转时，导体内将会产生涡流，而涡流又会产生磁场；此涡流产生的磁场与旋转的导体相互作用又将产生第2个涡流，然后产生第2个磁场；第2个磁场产生第3个涡流和磁场……因此，总的磁场由无限多个场组成，因最终的结果确定存在，所以多个场的和是收敛的，或者说，该过程是负反馈过程.

基于以上过程，本文采用简化模型来进行分析，如图4所示.建立坐标系，假设z轴为旋转轴，铝圆柱体的转动角速度为ω(逆时针方向).外场B0(假设均匀)方向指向y轴正向(实验系统中的铅垂方向)，感应磁场记为BI.

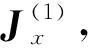
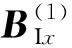
(a) 第1次迭代过程

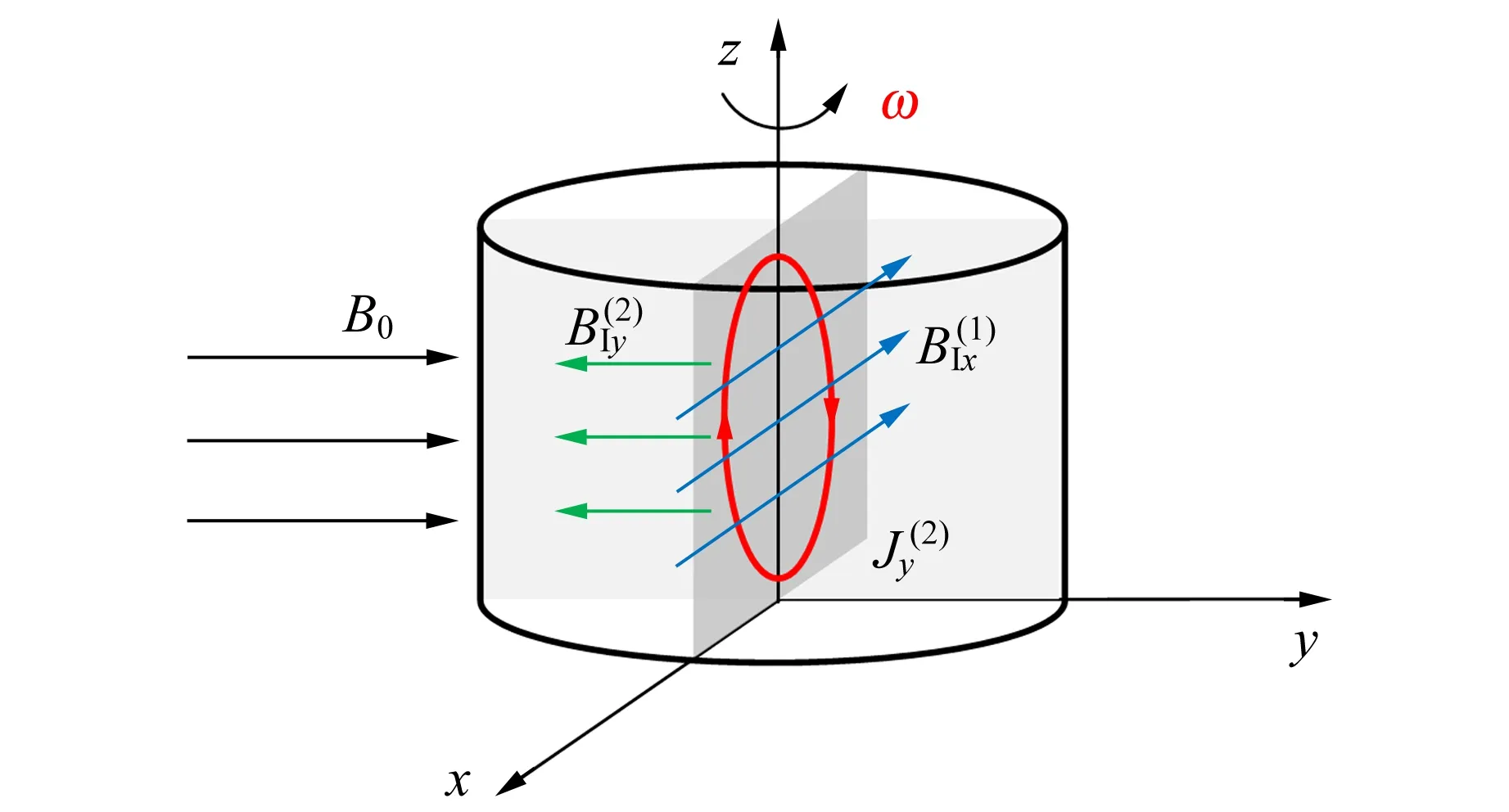
(b)第2次迭代过程图4 利用迭代过程分析电磁感应的物理图像

BIx=-βσωμ0rBTy=-αωBTy，

(2)

式中，负号表示BIx指向x轴的负方向，β是与导体形状及几何尺寸有关的常量，α=βσμ0r.

根据以上分析，同样可得到

BIy=βσωμ0rBTx=αωBTx,

(3)

考虑到BTy=B0+BIy，BTx=BIx，再联立式(2)和式(3)，可得感应磁场与角速度的关系为

(4)

(5)

感应磁场对永磁铁作用力的大小与磁感应强度大小成正比，如图4所示.磁体受到的升力(磁悬浮力)FL与y轴方向感应磁场的磁感应强度成正比(FL∝BIy)；磁体受到的拽力(阻尼力)FD与x轴方向磁场的磁感应强度成正比(FD∝BIx).

根据式(4)和式(5)，对图3的数据进行非线性拟合，结果如图5所示.从图中可以看出，实验测量结果与理论公式符合得较好，说明了理论分析合理.

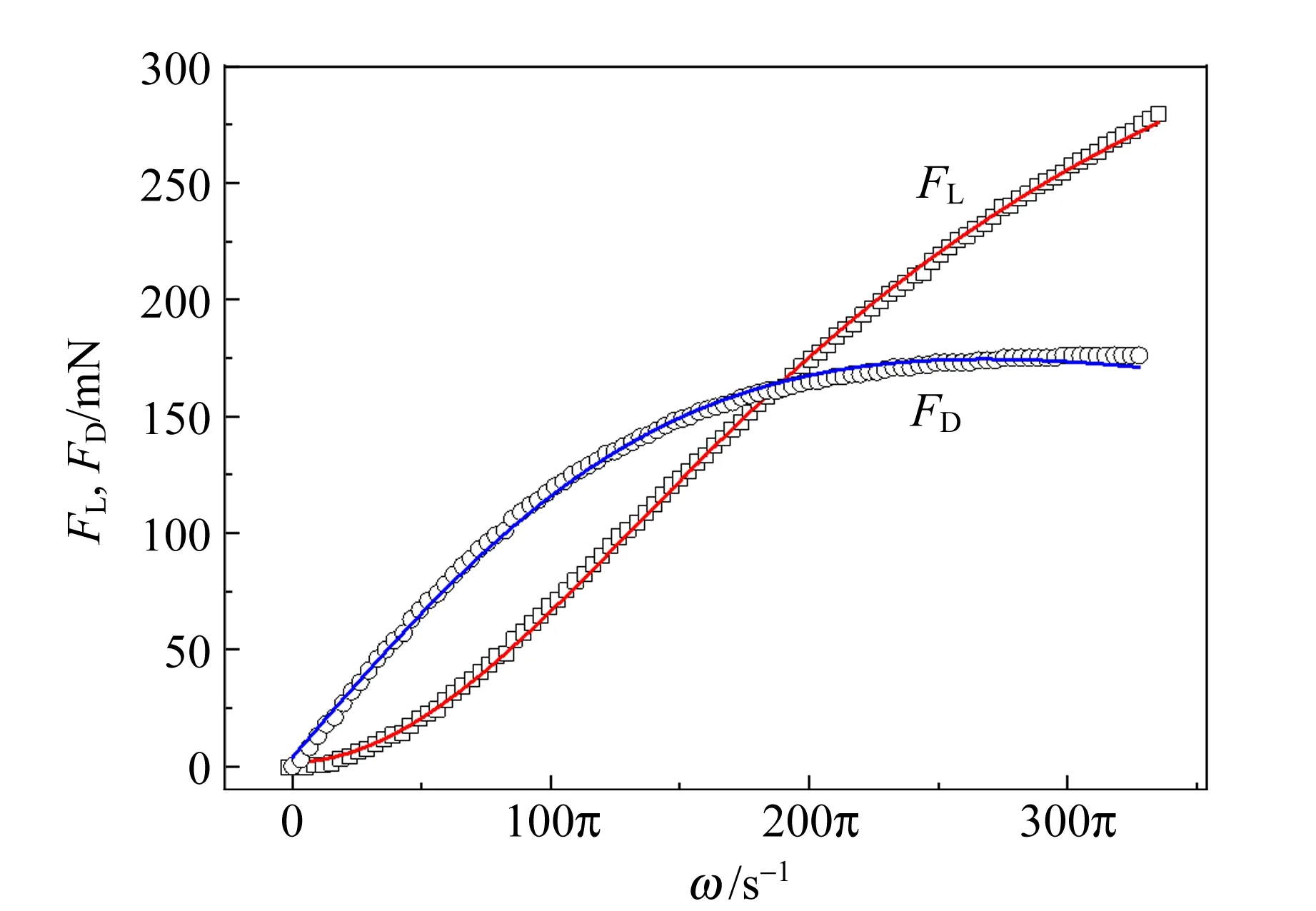
图5 磁体所受升力FL与拽力FD的实验数据与理论值

感应磁场与角速度的关系与磁场中旋转导体问题的理论计算及实验结果一致[13-14]，由此推导出的FL和FD与运动速度的关系，也与磁场中的平动导体问题的理论计算及实验结果一致[15].这说明式(4)和式(5)具有普适性.

2.2 感应磁场的特点

感应磁场BI=BIx+BIy，如图6所示.BIx沿x轴负方向，BIy沿y轴负方向，感应磁场BI与x轴的夹角为φ.根据式(4)～(5)可知，BIy∝ωBIx，且BIy随角速度增加的增速更快，故夹角φ随角速度的增加也会变大，即感应磁场将随着转速增加而逐渐旋转，其转动方向与导体柱的旋转方向一致.在极大转速的极限情况下，BIx→0，BIy→-B0，感应磁场将会与外场大小相等、方向相反(符合楞次定律)，导体内的总磁场趋于零.当然，这种状态不可能达到，因为随着转速增加,涡流的焦耳热会越来越多，从而会限制转速的无限增大.

为了更清楚地了解上述物理过程，本文使用霍尔片测量了靠近圆柱体表面处的磁感应强度，图6中标出了5个磁场测量点，其磁感应强度随转速变化的测量结果如图7所示.图7中的数据为感应磁场的磁感应强度，是总场强扣除外场之后的结果(先测出外场的磁感应强度).从图7中可以清楚地看到，随着转速的增加，磁感应强度的峰值点位置从1→2→3→4→5逐渐移动，说明了感应磁场在逐渐旋转.

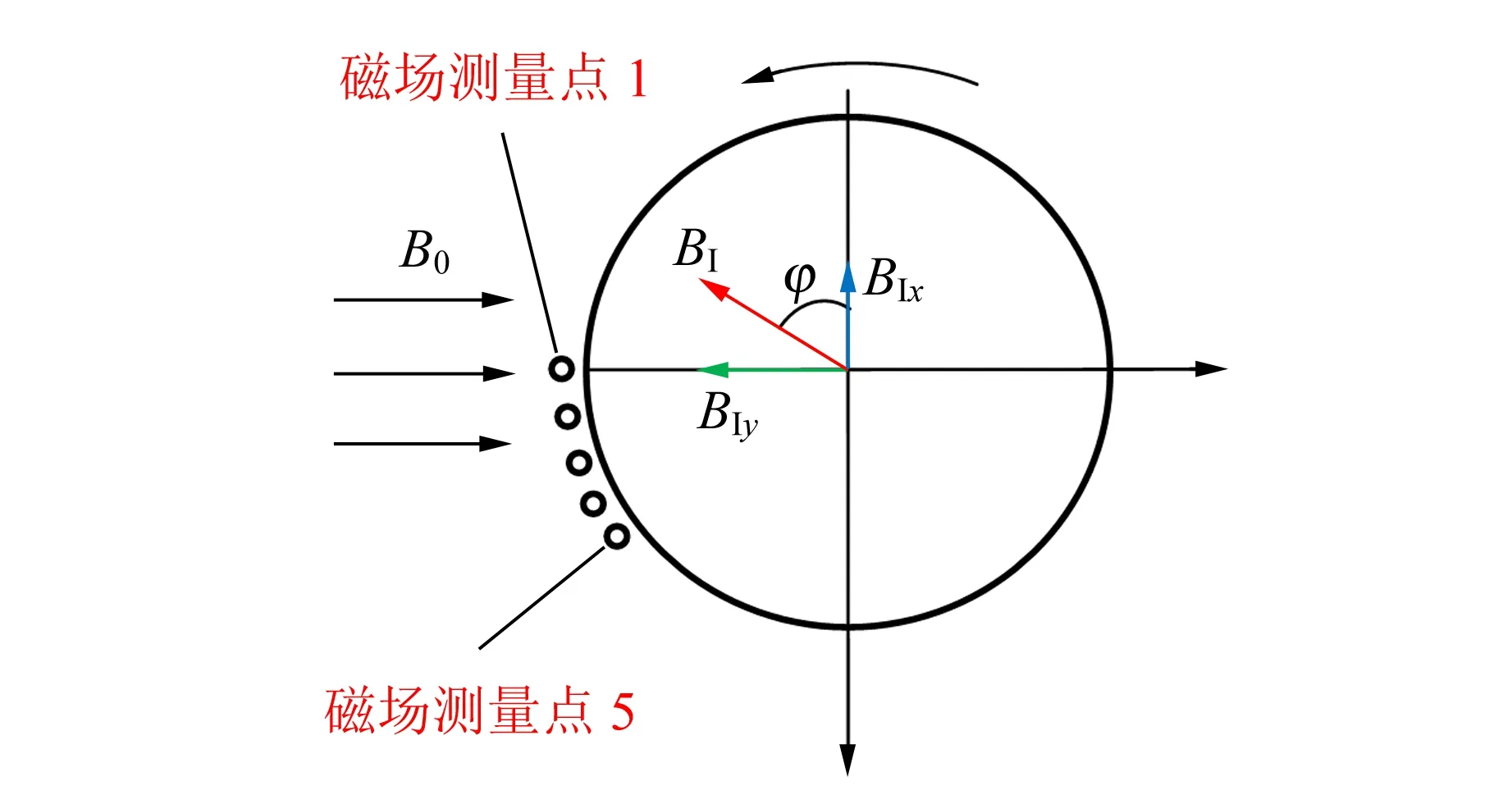
图6 感应磁场的特点

图7 不同位置处磁场的测量结果

3 测量与分析

为进一步了解磁体的受力情况，重新设计了测力传感器的分布.将永磁体等效看作电流恒定的矩形线圈，磁场向下时，左侧电流与右侧电流(红色线条)的流向如图8所示.在图示位置安装测力传感器，可分别测量磁体左侧的升力FL1和拽力FD1，同样可测量磁体右侧的升力FL2和拽力FD2.测量结果如图9所示.很明显，磁体左右两侧的受力情况有较大区别.特别是升力的测量结果，可以看到左侧受到向上的升力，右侧所受的力向下，在速度较低时，二者几乎同步增加，所以净升力较小，该阶段的磁体实际上受到绕对称轴(见图8)的力矩作用.接下来，随着速度的增加，磁体所受左侧的升力增速放缓，而右侧向下的力减小，所以总升力的增速基本持平.这是以前未观察到的变化过程，该现象同样可由上一节讨论中所指出的“感应磁场的指向随角速度增加产生旋转”的结论进行解释.

图8 力传感器位置示意图

(a)升力

(b) 拽力图9 永磁体左右两侧的升力和拽力

感应磁场是涡流产生的，可以用环形电流产生的磁场来大致模拟. 电流越强，磁力线越密集，感应磁场转动，磁力线方向也会随之转动. 与永磁铁等效的矩形线圈中的电流所受力的方向垂直于磁力线方向，因此可用磁力线方向的变化来解释作用力方向的变化，如图10所示.

1)转速ω很小的情况，如图10(a)所示. 此时涡旋电流很小，磁场的偏转角φ也很小，因此可以忽略，此时磁体总的受力情况F1+F2为：水平方向受到向左的拽力(与圆柱体上表面运动方向一致)，就好像磁体被下方导体拖拽一样；垂直方向所受的合力为0，但存在绕线圈对称轴的力矩.

2)转速ω稍大的情况，如图10(b)所示.此时F1和F2都有所增加.因磁场偏转了小角度φ，所以电流线圈处的磁力线方向也有所偏转，故电流线圈所受的安培力也会产生一定变化：水平方向所受合力仍是向左的拽力，而且变得更大；垂直方向的合力不再为0，而是受到向上的升力——磁悬浮力，其力矩仍存在.

3)转速ω较大的情况，如图10(c)所示.此时磁场的偏转角φ较大，线圈电流所受安培力的变化为：水平方向所受合力仍是向左的拽力，但力的增速变缓；垂直方向的合力(磁悬浮力)增加较快.

总之，随着ω的增加，涡流产生的磁场的磁力线密度在增加，方向也在旋转，导致F1和F2的大小在增加，方向也随之旋转.水平方向与垂直方向的合力的变化趋势为：随着ω的增加，水平方向的力总是向左，先是稳步增加，然后增速放缓，最后减小；垂直方向的力从0开始，逐渐出现稳步增加的升力，没有出现减小的趋势.

(a) ω很小

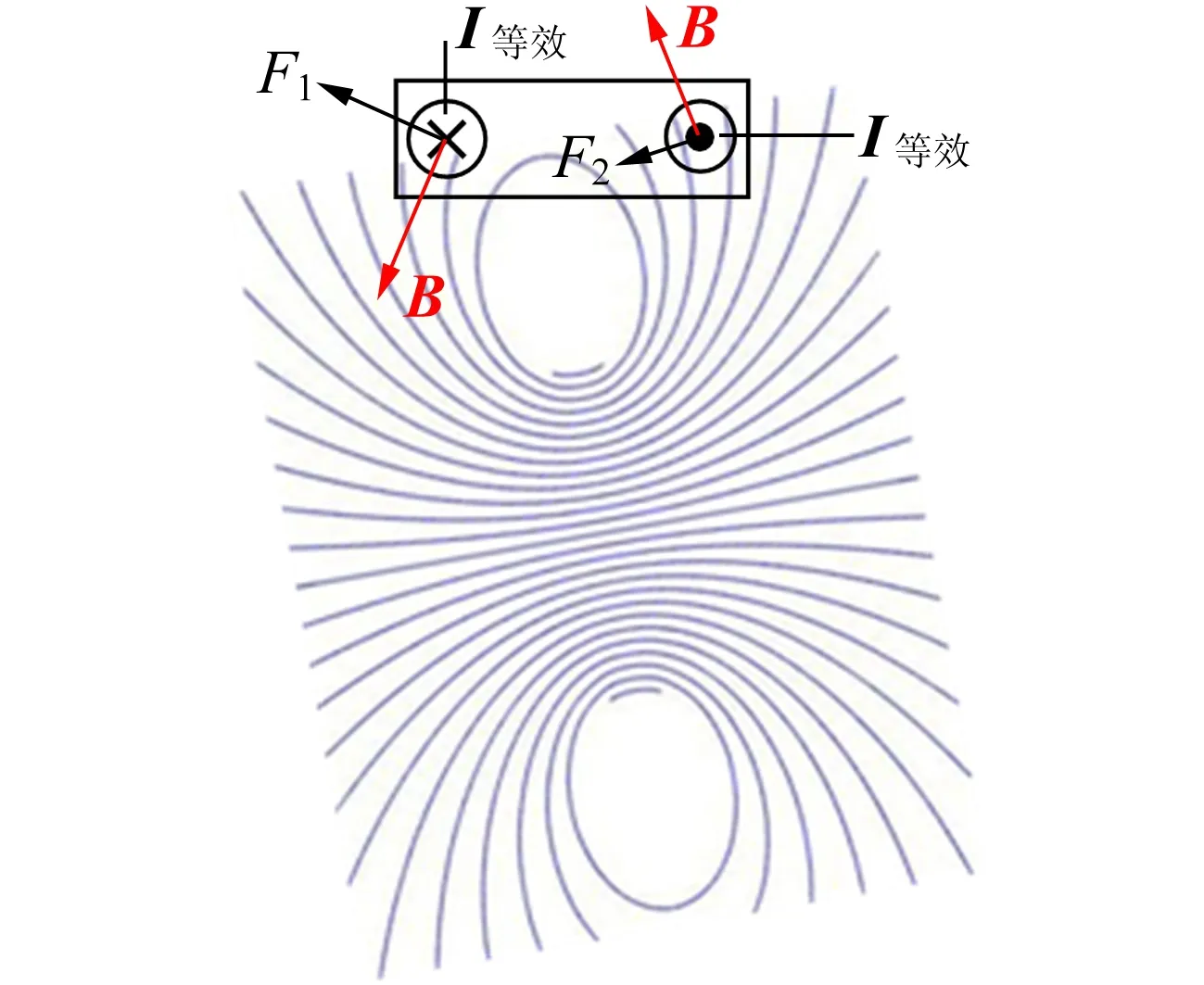
(b) ω稍大

(c) ω较大

图10 永磁体受力随磁场转动的变化

以上分析对应于图9中各阶段实测曲线的变化趋势，充分说明了“感应磁场的指向随角速度增加产生旋转”的正确性.

4 结 论

磁体与运动导体之间的相互作用是典型的电磁相互作用，了解它们因电磁感应产生的磁悬浮力与磁阻尼力，既具有理论研究的意义，又具有实际应用价值.本文设计并制作了研究这种相互作用的实验装置，对磁悬浮力、磁阻尼力以及感应磁场的磁感应强度等物理量进行了测量，并利用双梁力传感器对磁体前后两侧的受力进行测量，观察到了两侧作用力的变化.通过对涡流与磁场相互作用过程的分析，建立了用迭代方法描述的理论模型，得出感应磁场的方向随角速度增加发生旋转，并推导出了这些量与导体转动角速度之间的关系式，这些关系式与磁悬浮力、磁阻尼力的实测数据符合得较好.根据以上结论，可以很好地解释感应磁场的磁感应强度的测量结果，对磁体前后两侧受力的实测结果也能给出较好地解释.本文得到的结果具有一定的普适性，对磁体与运动导体之间的相互作用系统具有参考意义.