多形式浮式风机半潜式平台运动特性研究
张 轲,陈 兵
(大连理工大学,辽宁 盘锦 124221)
能源是关系到国家发展战略的问题,传统能源已不能满足国家可持续发展的战略需求,需要进行新能源的开发与探究。风能作为目前新能源的一种,具有存储量大、清洁等诸多优点,对其进行开发具有较大的意义。我国海上风能资源相当丰富,海上风能较陆上风能具有许多优势。海上风力发电成为新能源开发的重要的一个领域,目前海上浮式风机的研究得到了较为广泛的关注。
综合考虑经济与安全性,浮式平台基础一般采用单柱式平台(Spar)结构基础、半潜式结构基础以及张力腿平台(TLP)结构基础3类[1-3]。相对而言,半潜式平台具有一定优势,首先便于在码头上对平台进行建造、组装、调试甚至安装风力机,其次系泊系统安装成本较低,并且维修成本低。因此,当前海上浮式风机平台基础研究中,对半潜式平台的关注度较高。学者对海上浮式风机的研究多集中在平台运动水动力仿真、平台系泊系统优化、平台结构强度、各式平台对比等方面。在平台运动水动力仿真方面,2016年,阮胜福等[4]运用SESAM软件建立半潜式风电平台的有限元模型,分别计算其频域和时域运动响应,分析了该平台运动性能和系泊缆张力。2018年,施伟等[5]以南海海况下半潜浮式风机为研究背景,采用 ANSYS-AQWA 分析软件,对浮式风机在南海典型海况下的动力学响应进行了分析,探究了故障工况下半潜式平台的动力学响应。2020年,LI X等[6]采用OC4-5MW海上浮式风机系统,利用 FAST软件探讨了船舶的偏航误差和风浪偏差对海上浮式风力机动力特性的影响。在平台系泊系统优化方面,范子谦等[7]利用AQWA软件对某海上千瓦级垂直轴风机浮式基础及其系泊系统进行了水动力分析,并对浮式基础的系泊方式进行了安全校核计算。李秋辰等[8]参考英国Kincardine风机采用的新式Semi-Spar概念提出了一种新式海上浮式风机平台模型。利用AQWA软件进行了水动力计算,验证了新式平台可靠性,并进行了系泊系统优化。平台结构方面,2020年,ALSHUWAYKH A等[9]利用OpenFAST软件,对NREL 5 MW风力发电机在半潜式平台上进行了一系列受固定约束和自由移动配置时的仿真,得到平台运动与载荷差异之间的关系以及由此产生的疲劳,对风机设计有一定参考意义。平台形式对比方面,2019年, PHAM T D等[10]对750 kW半潜式平台风力发电机组进行了模型试验和数值模拟,通过改变平台干舷、轮毂高度等相关参数,进行了对比性研究分析。KIKUCHI Y等[11]基于日本5 MW风机的全面示范项目进行Spar、半潜式平台和驳船平台的建模,利用AQWA进行水动力分析,得到3个平台运动和系泊力的特性并进行了对比分析。
在上述国内外研究中,学者多采用基于美国可再生能源实验室(NREL)公布的 5 MW 风力机系统的OC4-DeepCwind模型,其次为荷兰的Tri-floater模型,以及其他形式的三浮筒式模型。在平台形式对比方面研究中,部分学者对Spar式、驳船式以及半潜式平台的浮式风机模型进行了水动力方面的对比。针对半潜式平台模型对比方面,一些学者进行了多种三浮筒式半潜式平台模型的对比,比如美国OC4-DeepCwind模型、Tri-floater模型、日本福岛未来紧凑式模型等。学者在各式平台对比的过程中,有的未控制各式平台模型的排水量保持一致。并且学者对其他半潜式平台的模型形式的关注相对较少,比如四浮筒形式的半潜式平台模型,包含浮舱结构的平台模型。因此,采用当前最为流行的OC4-5MW海上浮式风机系统的OC4-DeepCwind三浮筒式半潜式平台模型[4],并基于该模型,创新性地建立了四浮筒式半潜式浮式平台基础。同时参考传统油气开发半潜式平台模型,创新性地建立了两浮舱式半潜式平台模型。使得3个模型的排水量保持基本一致,利用ANSYS AQWA进行了平台性能的对比。考虑多种风浪流环境海况,采用相同系泊系统进行了时域分析,对比了3个模型的运动特性情况。发现排水量一致情况下,在一定风浪联合环境条件下,浮舱式结构在多种自由度下表现出一定优势。相对而言,浮筒式结构更有利于抵御流荷载。对在我国不同海域情况下,设计出更适用于特定海域环境条件的半潜式平台,有着一定的设计指导意义。同时,有利于以后设计出多种结构形式结合的性能优异的平台,对未来平台设计具有较高的参考价值。
1 理论基础
1.1 环境荷载
关于风载荷,一般采用海面以上10 m处的1 h平均风速并配以时变分量,以风谱的形式从能量的角度来描述风对于海洋工程结构物的影响。目前被海洋工程界广泛使用的风谱主要是API和NPD谱,在最新版本的API RP 2A中,NPD谱成为推荐风谱,因此本文采用NPD风谱进行风的模拟,其介绍如下[12]。
海平面以上z米处的1 h平均风速U(z)为:

式中,U(z)为海平面以上z米的1 h平均风速;U10为海平面以上10 m处的1 h平均风速。
NPD风谱描述了某点处纵向风速能量密度的波动,其表达式为:

式中,SNPD(f)为频率f的能量谱密度,m2/s;f为频率,Hz。
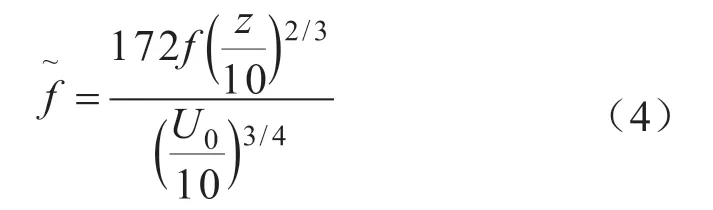
关于不规则波,工程界一般使用波浪谱的方式从能量分布的角度来模拟不规则海况,如PM谱、JONSWAP谱、TMA谱、Breschneider谱等。其中JONSWAP谱的使用十分常见,用于模拟我国南海不规则波海况,因此本文不规则波采用JONSWAP谱。

其中,

式中,TP为谱峰周期;γ为谱峰升高因子;σ为谱性参数;Hs是有义波高;A为无因次风区的函数;w为频率。
1.2 浮体运动幅值响应算子
浮体运动幅值响应算子(Response Amplitude Operaters,RAO)的含义是浮体对应自由度运动幅值与波幅的比,表明在线性波浪作用下浮体的运动响应特征。以船舶的横摇运动为例,横摇RAO为船舶在单位波幅的规则波作用下所产生的,关于波浪频率的横摇运动幅值函数,近似表达式见式(8):

式中,θX为船舶横摇运动幅值;ξa为入射波波幅,此处为规则波单位波幅;DAFRoll为横摇运动方程得到的动力放大系数;ω为入射波圆频率;β为入射波角度。上式单位为(°/m)。
RAO本质上描述的是线性条件下入射波幅与浮体运动幅值的关系。当对运动响应结果求一次导数、二次导数后,对应的运动RAO变为运动速度响应RAO和加速度响应RAO。
2 半潜式风机平台设计
NREL公布的OC4-5MW海上浮式风机系统由浮式平台、锚链系统、风机机舱、塔架组成。其中其风机机舱、塔架的主要设计参数如表1所示。

表1 OC4-5MW风机机舱、塔架主要设计参数
本文采用OC4-5MW海上浮式风力机系统的DeepCwind三浮筒式半潜式平台基础[4],参考相关参数,设计了四浮筒式风机平台基础,以及两浮舱式风机平台基础,利用SolidWorks建立了上述3个平台基础的三维模型。3个模型装机效果如图1所示。图中风机平台基础从左到右依次称为三浮筒式、四浮筒式、两浮舱式浮式风机,塔筒与风机均参照OC4-5MW海上浮式风机。该风力发电机的额定功率为5 MW,当切入风速达到3 m/s,风机开始工作;当风速达到11.4 m/s时,风机达到额定功率5 MW,此时风机发电效益较好。风机切出风速为25 m/s。
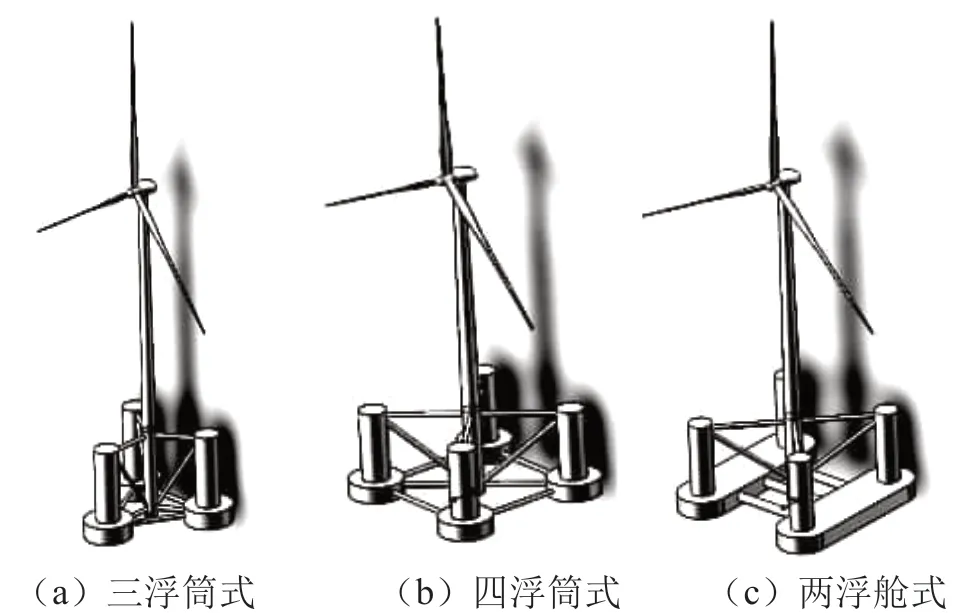
图1 3种半潜式平台装机模型: 三浮筒式、四浮筒式、两浮舱式
其中,3种半潜式浮式风机基础相关设计参数如表2所示:

表2 三浮筒式、四浮筒式、两浮舱式平台基础的 主要设计参数
如图1所示,上述3种平台均主要通过侧面浮筒或者浮舱提供浮力。在正常工作作业时,需要在各平台基础的浮筒或者浮舱中加入一定的压舱水来进行压舱工作,使得平台基础达到预定水位,最终,压舱完毕的平台基础及其系泊系统的重力与浮力达到相对平衡。其中三浮筒式浮式风机基础模型以最小网格尺度1.5 m进行网格划分,采用结构网格,单元数为16 579,节点数为165 48;四浮筒式风机平台模型以最小网格尺度1.2 m进行网格划分,采用结构网格,单元数为28 112,节点数为28 059;两浮舱式风机平台模型以最小网格尺度1.5 m进行网格划分,采用结构网格,单元数为18 082,节点数为18 064。图2为3个浮式风机平台基础进行网格划分后的数值模型。

图2 3种半潜式平台数值模型:三浮筒式、 四浮筒式、两浮舱式
3 风荷载的施加
对于风电机在正常发电的风载荷(本文只计算水平气动推力),按照《风力发电机组设计要求》(JB/T10300—2001)计算,并计入风力系数之中[13]。考虑在风机正常发电时,作用在风轮扫掠面积上的平均压力PH由下式确定。

式中,ρa为空气密度,一般采用ρa=1.297 kg/m3;CFB为系数,根据贝茨公式可取CFB=8/9;u为风速。
正常发电时,作用于塔架顶部即轮毂处的水平风力为:

式中,A0为风轮扫掠面积,指的是风轮在旋转平面上的投影面积;D为叶轮直径。
4 时域分析
4.1 系泊系统
关于系泊系统:根据规范DNV[14-15]的相关建议,采取公称直径78 mm的有档系泊锚链(R3),其相关参数为:空气中重量133 kg/m,水中重量122 kg/m,轴向刚度6.433×107kN·m-2,断裂力5 123 kN,拖曳力直径0.076 mm,附加质量系数1.0,拖曳力系数1.2,轴向拖曳力系数0.4。三者使用相同的系泊悬链式系统,并按照侧浮筒个数均匀布置,每个系泊缆依次给出标号进行设定,如图3所示。

图3 三浮筒式、四浮筒式、两浮舱式系泊系统布置
4.2 环境条件
浮式风机在正常工作情况下,会受到多种环境荷载的影响,比如风、浪、流等常见海域荷载。为更好地探究3种浮式风机平台的环境适应能力,采用多种荷载联合作用的环境条件。我国南海风力资源丰富,有研究表明,南海东沙群岛、西卫滩附近海域出现波高的极大值点,其一年一遇的最大波高为2.7 m[16]。故波浪波高采用各季节中的常见波高,波浪谱为JONSWAP谱的不规则波,谱峰因子保持3.3不变。关于风荷载,5 MW浮式风机的额定风速11.4 m/s,此时达到其额定运行功率,研究此风速荷载下风机平台基础的运动响应有较大意义。故采用NPD风谱,1 h内平均风速为11.4 m/s。海表面流流速采用0.9 m/s。其中风、浪、流的方向均为0°方向,如图3所示,即风机的完全迎风方向保持一致,相关工况见表3。

表3 多种环境条件工况定义
4.3 时域分析结果
在影响浮式风机运动响应的环境荷载中,风与浪的影响是最大的,因此考虑1、2、3工况下,风浪联合作用时,不同谱峰周期的JONSWAP谱对各式浮式风机平台基础的运动响应的影响。如图4所示,为在风浪荷载联合作用的1、2、3工况下,各浮式风机平台的纵荡、横荡、垂荡、横摇、纵摇、艏摇6个自由度的运动幅值情况的统计值。由于3种浮式风机平台基础的形状结构、质量分布有较大差异,造成其各固有频率的不同,因而不同谱峰周期的JONSWAP谱不规则波对其造成的影响有着一定差异。

图4 3种平台的六个自由度时历响应统计值随谱峰周期变化图
图4结果显示:在纵荡、横荡、横摇、艏摇四个自由度方面,三浮筒式风机平台在1、2、3工况(分别对应谱峰周期为5 s、10 s、15 s)下的运动响应最大值较其他式风机基础均为最大,其次为四浮筒式,而两浮舱式的值最小;在垂荡自由度下,三者运动响应最大值均不大,三浮筒式和四浮筒式均在1.3 m左右且较为接近,两浮舱式在各工况下最大;在纵摇自由度下,三浮筒式在3工况下运动转角均为最小,其他工况四浮筒式最小,两浮舱式在所有工况中均最大。由于风、浪的作用方向均为与x轴夹角为0°的方向,因此三者运动响应幅值的最大值在纵荡、纵摇均表现得比较明显。而三浮筒式在横荡、艏摇方面表现出较大运动响应最大值,可根据其锚泊系统中系泊缆相关受力进行一些分析,如图5所示。

图5 三浮筒式、四浮筒式、两浮舱式系泊缆顶端张力时历曲线图(工况1)
在该风、浪入射角度下,三者均有两个系泊缆受较大张力,并且四浮筒式和两浮舱式的受力较大的系泊缆(1、2缆)受力随时间的变化趋势几乎一致。而三浮筒式的受力较大的系泊缆(2、3缆)受力情况重合性不如其他两者,反映了其在横荡、艏摇方面出现了较大的运动。俯视角度下三浮筒式1缆的布置与风、浪入射角度重合,且只有缆1在最初时间段进行张力的卸载。在缆1张力的卸载到一定程度时,由于其他两个缆具有一定弹性,也会进行力的卸载,会导致缆1的舒张。上述过程可以在图5中最初时间段可以明显观察到,而三浮筒式是在最初缆1的舒张过程中,其他两缆受力开始不重合,即出现一定的横荡、艏摇运动。三浮筒的缆1最初在对称轴上,且只有一个,在该入射风、浪荷载作用下,会出现一定的振动现象,难以保持在对称轴上,便会引起不对称性。而其他两式的3、4缆的布置则能保持较好的对称性,因此导致三浮筒式比其他两式在横荡、艏摇方面出现较大的运动。由图5可知,各式浮式风机平台系泊系统在时域分析中,其系泊缆始终满足缆的强度设计要求,表明该工况下,此系泊系统布置可行。由于系泊系统合理均匀布置,三者在6个自由度的运动响应平均值除纵荡方面均表现得较小。在纵荡方面,三者在3种工况下的运动响应平均值,依然是三浮筒式最大,其次是四浮筒式,两浮舱式最小。
在进行时域分析前,对各式平台进行了规则波波浪的频域水动力分析,以探讨其各自由度方向的固有频率,采取多频率周期及多浪向的入射波荷载。结果表明,各式平台在纵荡、横荡方向,其RAO均在波浪周期为 5 s 左右时表现出一个峰值;垂荡方向,三浮筒式、两浮舱式表现出一个极大值和一个极小值,两者的极大值分别在波浪周期 10 s、15 s 附近,极小值分别在 15 s、30 s 附近。四浮筒式则分别在 5 s 左右、10 s 左右表现出两个极大值,在 7.5 s 左右、13 s 左右表现出两个极小值;横摇方面,三浮筒式、四浮筒式均分别在波浪周期为 10 s 左右、20 s 左右达到极大值,且 20 s 达到最大值。而两浮舱式分别在 5 s 左右、10 s 左右的规则波波浪周期时达到两个极大值,于波浪周期为 10 s 处达到其最大值;艏摇自由度方面,三浮筒式、四浮筒式均分别在波浪周期为10 s 左右、20 s 左右达到极大值,且 20 s 达到最大值。两浮舱式于 3~5 s 左右有一极大值,另一个极大值在如 0°等多个浪向下于 5 s 左右达到。由上述可知,波浪周期为5 s时对各式平台影响较大,图6即为工况1下,5 s周期规则波分量作用于各式平台于10 025 s时的所受压力云图,可以观察出各式平台所受压力分布及大小,其中蓝色越深表示越小,黄色越深,甚至达到红色表明压力越大。
图6 三浮筒式、四浮筒式、两浮舱式10 025 s时压力云图(周期5s规则波分量)(工况1)
在对比各工况下各式浮式风机平台各自由度运动响应最大值之后,各式浮式风机平台在风浪荷载联合作用时,各自由度对应的不规则波的谱峰周期的响应敏感度是不同的。三者在纵荡自由度下,四浮筒式、两浮舱式在1工况均表现出最高值,表明谱峰周期为5 s的JONSWAP谱对两者在纵荡自由度的影响最大,其含有的波浪频率更接近四浮筒式、两浮舱式平台纵荡自由度的固有频率。三浮筒式在工况3下达到最大值。在一些自由度中,平台的运动响应最大值表现出与不规则波谱峰周期变化趋势表现一致或相反的趋势。如在横荡自由度下,随着不规则波谱峰周期的增大,三浮筒式的运动响应最大值逐渐减小,而四浮筒式与两浮舱式运动响应最大值逐渐增大。垂荡自由度下,两浮舱式运动响应最大值与不规则波的谱峰周期变化趋势保持一致。横摇自由度下,两浮舱式与四浮筒式运动响应最大值与不规则波的谱峰周期变化趋势保持一致,而三浮筒式则表现为相反趋势。纵摇方面,三浮筒式和四浮筒式与不规则波谱峰周期变化趋势保持一致。艏摇方面,三浮筒式运动响应最大值与不规则波的谱峰周期变化趋势保持相反,而四浮筒式、两浮舱式运动响应最大值保持一致。
为探讨流荷载对各式风机平台的影响,故考虑对比在工况1与工况4时,各浮式风机平台在各自由度方向上的运动响应值的最大值与平均值如表4所示。

表4 3种平台的六个自由度时历响应统计值(工况1与工况4)
工况1与工况4是相同的风、浪荷载,而工况4含有流荷载的施加,是风浪流联合作用的工况。如表4所示,由于流荷载的施加,3种浮式风机平台的在六个自由度的运动响应平均值的绝对值,除三浮筒式在横荡自由度下均有所增加。特别在该角度下入射影响最大的纵荡、纵摇两个自由度,三者的平均运动响应值增加得更为明显一些。在运动响应最大值方面,纵荡、纵摇、艏摇3个自由度,三者均增大,横荡、横摇方面,三浮筒式与四浮筒式均减小,而两浮舱式增大。垂荡方向三者运动响应变化不大,只有四浮筒式增大。
由于纵荡、横荡、艏摇3个自由度三浮筒式风机平台的运动响应最大值较大且变化较为明显,因此对比其3种自由度下的运动响应变化值有着一定的必要性,如图7至图9分别为3种浮式风机平台在工况1与工况4下的纵荡、横荡、艏摇自由度的在运动稳定之后的9 500 s到10 800 s的时历响应曲线对比图。

图7 三浮筒式、四浮筒式、两浮舱式纵荡方向运动 响应时历曲线图

图9 三浮筒式、四浮筒式、两浮舱式艏摇方向运动 响应时历曲线图
如图7所示,受流荷载施加影响,3种风机平台在纵荡自由度方向上,三者的平均值均有着明显的增大趋势,分别增加24.65%、13.00%、12.88%。而纵荡方向运动位移最大值分别增大了11.63%、7.76%、16.44%。三者的标准差分别由4.06到3.16,由2.65到2.10,由2.21到1.99,均呈现出递减趋势,分别递减22.19%、11.79%、9.99%。因此在上述海况条件下0°方向风浪流联合运动中,流荷载对平台纵荡方向运动响应的影响上表现为使得平台运动响应平均值、最大值均有着一定的增幅,而运动响应标准差减小。
如图8所示,受流荷载加入的影响,3种风机平台在横荡自由度方向上,三浮筒式、四浮筒式运动响应有着明显的减小,而两浮舱式有着明显的增大,其最大值分别变化百分比为-36.84%、-48.75%、881.25%。由于结构对称性和荷载对称性,三者平均值均接近于0,变化趋势和最大值一致。三者的标准差变化趋势与最大值同样一致,分别由8.36到4.7、由1.53到0.74、由0.03到0.48。由此可知,在横荡方向,流荷载的施加,对两浮舱式平台的影响较大,均有增大的趋势,而三浮筒式、四浮筒式却有减小趋势。
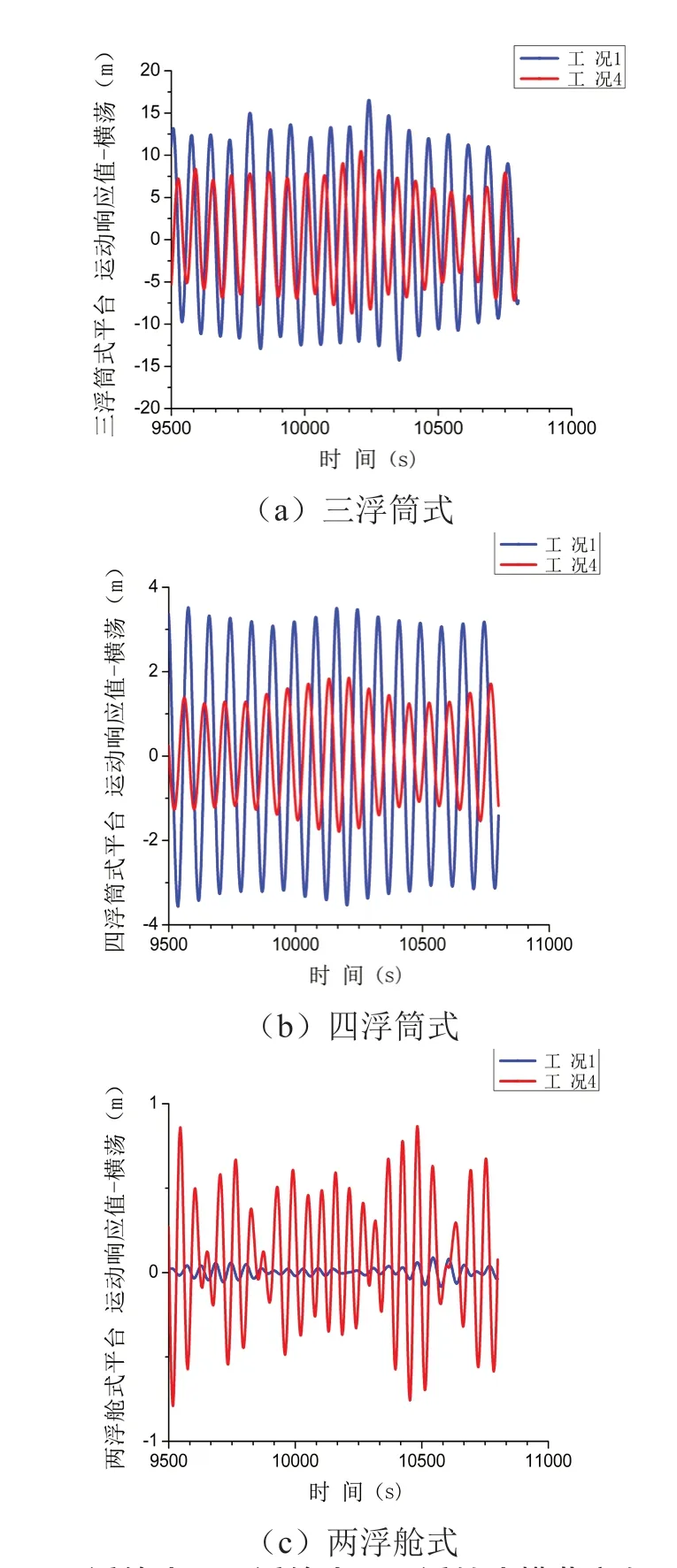
图8 三浮筒式、四浮筒式、两浮舱式横荡方向运动 响应时历曲线图
如图9所示,流荷载对三者在艘摇自由度的运动响应的最大值、平均值均有增大的影响,三浮筒式、四浮筒式、两浮舱式的艏摇运动响应最大值增大幅度分别为4.29%、35.14%、892.86%,即使两浮舱式该方向上的运动响应值仍然较小,但其增长幅度较大。三者在运动值的标准差均有增大趋势,分 别 由9.14到9.33、0.60到0.78、0.08到1.29,增大幅度分别为2.12%、29.92%、1 591.56%。
图7至图9的结果分析表明,在上述分析环境条件下,即沿着浮舱较长面方向来流时,平台浮筒式结构相对浮舱式结构,其主要运动方向即纵荡、横荡、艏摇方面的运动响应,流荷载的施加引起较小的变化,因此浮筒结构更具备抵御此来流方向的流荷载的能力,为以后的平台设计提供了一定的参考。
针对风、浪、流荷载联合作用的情况,为探讨JONSWAP谱有义波高对各浮式风机平台运动响应的影响,工况4到工况7环境条件的变化只是不规则波有义波高的变化。为更为清楚地观察其综合影响趋势,对3种浮式风机基础在各波况下各自由度下的运动响应最大值,分别进行了线位移的矢量和叠加及角位移矢量和叠加。工况4到工况7的环境条件下,3种浮式风机平台线位移矢量和及角位移矢量和最大值随不规则波有义波高变化情况如图10所示。

图10 3种浮式风机平台线位移矢量和与角位移矢量和最大值随有义波高变化图(工况4到7)
由图10可知,在上述风、浪、流联合作用的海况,改变不规则波有义波高的情况下,3种平台的运动响应的线位移矢量和最大值随着有义波高的增大而增大。三浮筒式的角位移矢量和最大值随波高的增大而先减小后增大,其他两者均有减小趋势,三者变化值均不太明显。无论线位移矢量和还是角位移矢量和,三浮筒式的值均始终大于四浮筒及两浮舱的值。对于运动响应最大值线位移矢量,四浮筒式的值保持大于两浮舱式的值。而对于运动响应最大值角位移矢量,两浮舱式的值保持大于四浮筒式的值。
由上述各式平台运动特性可知,工况4到7下,各平台工况4位移运动响应最大,因此下面进行工况1到4下锚泊缆顶端张力的校核。图11为各式平台受力最大系泊缆随时间的变化图,为便于分析,取0~1 000 s部分,且选择各式系泊缆张力最大的缆进行对比。显然三浮筒式的两个缆受力最大值较大,并且其变化剧烈程度明显高于其他两式的系泊缆张力。而四浮筒式1号缆和两浮舱式的1号缆两者顶端张力值相近,大小交替进行,整体上四浮筒式于较多时刻低于两浮舱式。校核各式平台各缆于所有时刻的顶端张力,各工况下系泊缆最大值如表5所示,显然各式平台系泊系统均满足强度要求,系泊系统布置合理。

图11 3种平台的锚泊缆顶端张力时历曲线图
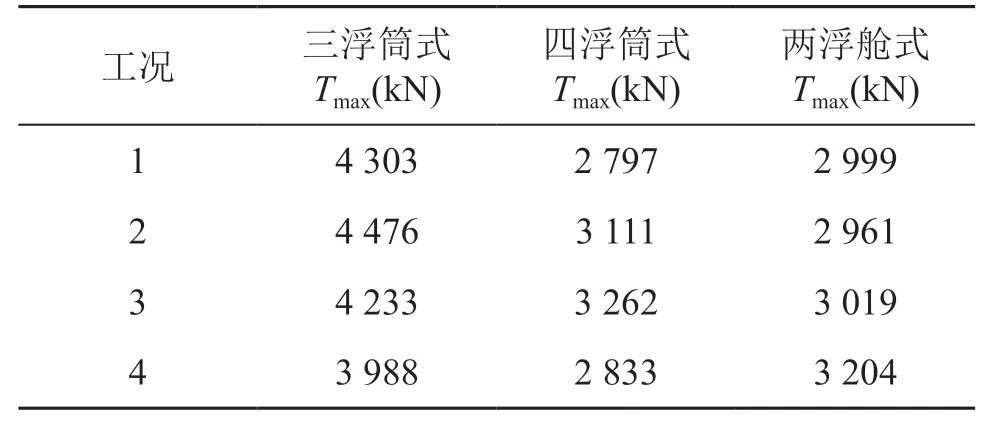
表5 3种平台的锚泊缆顶端张力最大值(工况1到4)
5 结 论
本文采用OC4-5MW海上浮式风力涡轮机系统的DeepCwind半潜式平台模型[1],并建立了四浮筒式和两浮舱式风机平台基础,分析风机工作时的受力情况,加入风力系数中,通过使用ANSYS-AQWA软件在一定海况下进行时域分析,得出以下研究结论。
(1)在风浪联合作用的工况下,在不规则波的频谱周期变化时,对于3种浮式风机平台基础的最大值运动响应,三浮筒式平台在纵摇自由度有优势,在垂荡自由度下,三浮筒式和四浮筒式均有优势,两浮舱式在纵荡、横荡、横摇、艏摇四个自由度有优势。
(2)在文中系泊系统布置及海况条件下,两浮舱式只在纵荡运动平均值表现的增幅最小为12.88%。其他方面均变化明显。流荷载的施加,运动响应最大值方面,三浮筒式、四浮筒式以及两浮舱式在纵荡方向分别增大了11.63%、7.76%、16.44%,横荡方向变化为-36.84%、-48.75%、881.25%,于艏摇方向增大幅度分别为4.29%、35.14%、892.86%。因此流荷载的施加对两浮舱式纵荡、横荡、艏摇3个自由度方向的运动响应影响最大。在横荡方面,三浮筒式、四浮筒式表现出明显减小趋势,而纵荡、艘摇方面增幅不大,可能与其共有的浮筒结构相关。可知浮筒式结构更有利于抵御流荷载,可根据相关海域环境,进行综合设计平台结构,综合利用浮筒式与浮舱式的设计,达到更为优异的性能。
在不规则波波浪有义波高变化的风浪流联合作用工况下,四浮筒式风机平台的运动响应最大值的线位移矢量和最小,在17 m左右。两浮舱式风机平台的运动响应最大值角位移矢量和最小,在3°左右,三浮筒式的值均始终大于四浮筒的值及两浮舱的值,分别在30 m和21°左右。各式风机平台的运动响应线位移矢量随不规则波有义波高的增加而增大,角位移矢量和变化不明显。

