城市生活垃圾分类回收处理PPP项目运作模式的政企民博弈分析

刘光富，陈子凡

（同济大学，上海 200082）

1 研究现状与研究目的

城市的不断扩张和居民数量的不断增长对现代城市提出了更高的要求。随着生活垃圾产生量的逐年增加，我国已成为世界上生活垃圾产生量最大的国家之一。如此多的垃圾不仅占用土地资源，而且产生有害物质，危害人类健康，如何应对已成为一项紧迫的任务。

2017年，财政部、住房城乡建设部、农业部、环境保护部联合发布《关于政府参与的污水、垃圾处理项目全面实施PPP模式的通知》，明确指出政府参与的污水、垃圾处理项目全面实施政府和社会资本合作（PPP）模式。截至2020年10月，废物分类、回收和处理行业共有920个PPP相关项目，约占我国PPP项目总数的1/10。

与其他PPP项目不同，废物处理PPP项目具有显著的外部性，因此高质量保证非常重要。然而，目前垃圾处理PPP运营模式的推广效果令人担忧，引发了一系列社会问题， “一勺炖”方式产生的废气形成了二次污染，严重危害当地居民的生命和健康。

近年来，国内外学者针对城市生活垃圾分类回收的运行模式进行了研究。城市生活垃圾处理各阶段利益相关者之间的博弈也是一个研究热点。刘承毅和王建明[1]构建了政府监管机构与企业之间的博弈模型，分析了声誉激励和社会监督对博弈双方盈亏的影响及其对策。叶健飞等[2]研究了垃圾分类和垃圾处理的博弈问题，构建并分析了居民博弈、政府与居民博弈、政府与企业博弈的演化博弈模型，并指出要构建完善的垃圾分类回收逆向物流网络，应重点关注政府的处罚及其监管成本、居民支付的总支出等因素。考虑到声誉对PPP项目监管的影响，李小莉[3]构建了一个进化博弈模型，发现当声誉对收入的影响达到一定水平时可以有效地促进公共部门和私营部门提供优质的公共服务。因此，有必要引入监督制度和激励制度，以纠正演进路径的发展方向。

目前国内外的演化博弈应用研究主要集中在政企两群体演化博弈方面，针对三群体进行演化博弈分析的研究成果较少。郭雪萌等[4]通过研究发现公众参与是提升政府监管绩效的有效方法。关于公众参与对政府监管绩效的影响研究，王树文等[5]认为公众参与能弥补政企信息不对称的不足，但是大多数学者忽视了公众参与的重要作用。

政府、公众和垃圾回收厂是生活废物回收市场的3个主要利益相关者。然而，政府监管的低效率、回收产品的低质量以及公众对回收产品的低接受度对我国垃圾回收市场的可持续性构成了挑战。本文通过建立一个三方博弈模型，研究了在生活垃圾回收市场中地方政府、公众和垃圾回收厂的策略是如何变化的。

2 基本假设与模型构建

博弈发生在不完全信息条件下，博弈三方为政府机构、垃圾处理企业与社会民众，三者均为有限理性的经济人。在有限决策能力与选择能力的约束下，三者根据以往经验或惯例做出决策或采取行动，并以追求自身利益最大化为目标。

1）假定政府机构策略集为S1={监管，不监管}，其中采用“监管”与“不监管”策略的比例分别为x和1-x（0＜x＜1）；垃圾处理企业策略集S2={合规，违规}，其中采用 “合规”与 “违规”策略的比例分别为y和1-y（0＜y＜1）；社会民众策略集S3={参与，不参与}，其中采用 “参与”与“不参与”策略的比例分别为z和1-z（0＜z＜1），“参与”指民众需向处理企业支付一定费用，以及参与企业治理效果的监督工作。

2）影响政府机构策略的损益变量：在“监管”策略下，获得上级政府发放的监管补贴为Su，政府在监管方面的成本为Cr，增加的社会效益为M，政府实施激励的成本为Sa，收取的罚款为Sb，政府的额外治理成本为Cp，政府社会公信力水平提升为Rr，政府对社会民众给予的举报奖励为Rd(＜Sb)；在“不监管”策略下，政府对污染的治理成本为Cp2，Cp2＞Cp，政府付出的成本为Cu，面临的声誉损失记为Rp1和Rp2，Rp1＞Rp2。政府得到的社会福利效益提升为Mg，降低为Vg。

3）影响垃圾处理企业策略的损益变量：合规处理的经济收益为Q，违规策略带来的额外收益为ΔQ，政策鼓励补贴为Sa，一定的惩罚为Sb，企业会得到一定声誉为Rp3，声誉损失为Rp4，企业额外损失为ΔS。

4）影响社会民众策略的损益变量：民众产生的效用为U1和U2，支付给企业的垃圾处理费用为F，向相关监督检查部门投诉付出的成本为Cd，心理损失记为N。

5）假设所有参数都为正数。

根据上述假设，可以得到不同决策情景下政府机构、垃圾处理企业和社会民众的收益矩阵，分别见表1和表2。

表1 民众参与时的收益矩阵

表2 民众不参与时的收益矩阵

3 演化博弈模型分析

3.1 模型的演化

在PPP项目中，政企民三方博弈者通过学习和反复尝试的过程来调整策略，从而重现演化博弈论描述的动态复制过程。

复制动态方程是一个动态微分方程，该方程基本上决定了一个特定策略在人群中被采纳或者被接受的频率[6-7]。

政府机构的复制动态方程为

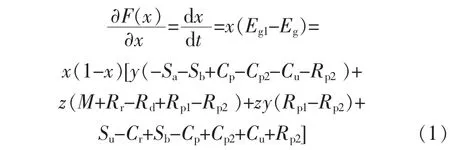
垃圾处理企业的复制动态方程为

社会民众的复制动态方程为

3.2 模型的分析

在该演化博弈过程中，如果令F（x）=0，F（y）=0，F（z）=0，可得到9个均衡点，分别为E1=（0，0，0）、E2=（1，0，0）、E3=（0，1，0）、E4=（0，0，1）、E5=（1，0，1）、E6=（1，1，0）、E7=（0，1，1）、E8=（1，1，1）、E9=（x，y，z）。其中，E1~E8这8个点是纯策略下的局部均衡点，E9是混合策略下的局部均衡点。根据这些假设，任何初始点及其演化点都必须在三维空间V={（x，y，z）|0≤x≤1，0≤y≤1，0≤z≤1}中，E1~E8这8个点所包围的区域就是这个演化博弈的平衡解。E9点仅在0＜α*＜1且0＜β*＜1的条件下存在。

系统的局部均衡点数量已确定，但是这8个点是否具有演化稳定的特点还需要进一步讨论。根据张焕玮和刘继滨[8]的思想，对该系统的雅克比矩阵进行局部均衡点稳定性分析。

考虑到参数的不确定性，在以下10种情况下考虑平衡点的稳定性，系统平衡点的稳定性分析结果见表3。

表3 平衡点及局部稳定性

4 数值实验及结果分析

为了更加直观地分析三方博弈过程的演化路径和最终的稳定状态，本文将变量具体化为真实数值，利用MATLAB软件分别模拟3种情景下的演化稳定策略，每组参数取值均需满足文中模型假设。

出于一般考虑，本文假设所有外生变量均为正。为了比较分析，第一个平衡态缩写为BAU1，第二个平衡态缩写为BAU2，第三个平衡态缩写为BAU3。用BAU1检验均衡战略B1（1，0，0）的稳定性和影响企业战略选择因素的敏感性；用BAU2检验均衡战略B2（1，1，0）的稳定性和影响政府战略选择因素的敏感性；用BAU3检验均衡策略B3（1，1，1）的稳定性和影响民众策略选择因素的敏感性。

采用MATLAB R19a进行仿真，仿真周期为60，初始时间为0，终止时间为60，步长为0.1，以三方积极选择策略的概率为主要衡量标准。通过以上分析可知，当博弈者的初始状态是采用纯策略时，他们的策略选择是0和1。

系统中没有一个参与者愿意改变当前的平衡状态。然而，这并不意味着均衡状态是稳定的，当一个或多个参与者做出一个小的调整时，均衡状态就会改变。在这里，博弈模型中涉及的外生变量的基值是使用文献中的方法确定的。只要参数设置满足理论分析的前提条件，尺度就可能发生变化，建模的结果也不必是常数。

情景1：Sa+Sb+ΔS-ΔQ＜0，-F-Cd+Rd＜0。输出结果见图1。从图1可以看出，最终系统演化稳定于（1，0，0），与复制动态分析结果完全吻合。

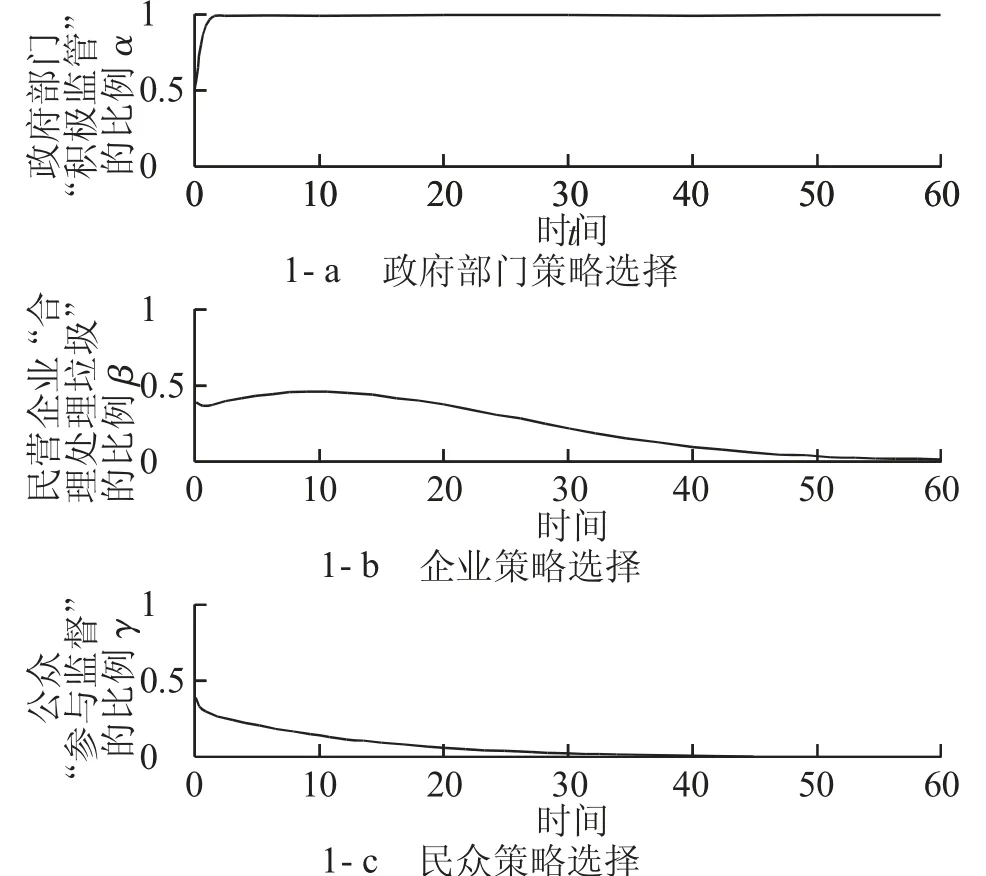
图1 平衡点1仿真结果

情景2：Su-Sa-Cr＞0，-F-Cd+Rd＜0。其输出结果见图2。从图2可以看出，最终系统演化稳定于（1，1，0），与复制动态分析结果完全吻合。

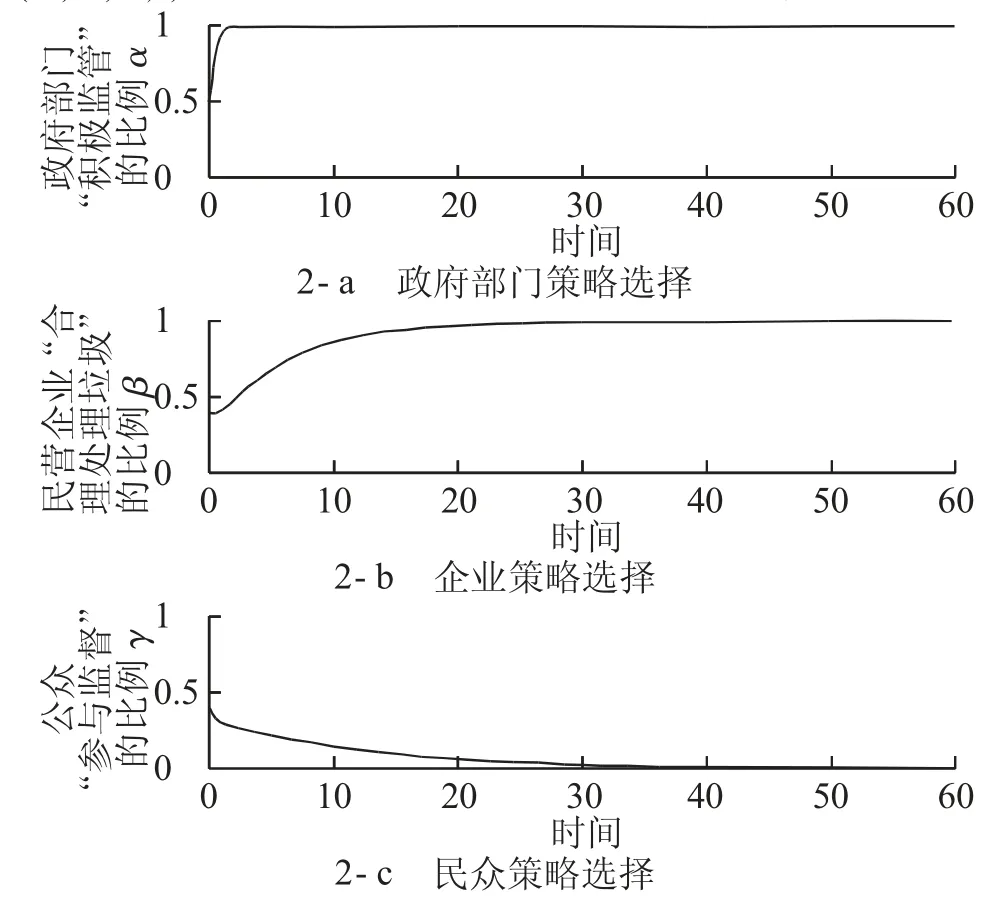
图2 平衡点2仿真结果

情景3：F+Cd-Rd＜0，-M+Sa-Rr+Rd-Su+Cr＜0。输出结果见图3。从图3可以看出，最终系统演化稳定于（1，1，1），与复制动态分析结果完全吻合。

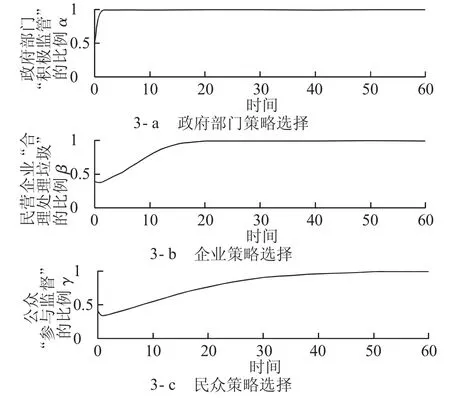
图3 平衡点3仿真结果

5 结论与建议

研究表明，政府在城市固体废物分类、回收和处理PPP项目中应采取“积极引导和监督”的行为，这一措施受多种因素的影响。从这个角度出发，为政府部门提出以下建议：一是加快相关政策法规的制定和实施，及时相互交流和学习经验，根据本地特点推出适合本城市的政策和指导方针，为PPP模式在城市生活垃圾分类回收领域的实施提供有力保障；二是正确定位，明确权责，提高声誉水平，给予公众和企业一定的空间，明确各方的权利和责任，通力合作，不越界，对社会资本给予绝对信任，实现共赢。

为处理企业提出以下建议：一是正确评估自身实力，全面分析项目，包括了解项目的过去和现在的使用寿命以及项目本身的建设条件，尽可能为自身和项目带来可观的价值；二是与政府合作，合理利用城市资源，不断提高效率，减少环境污染。企业积极配合政府，巧妙利用城市各种资源，这样更有利于项目的顺利进行。

生活垃圾处理服务PPP项目中公众的行为决策部分受政府和企业的行为决策影响，部分受项目的环保性质和项目本身的宣传程度影响。为此，对公众提出以下建议：作为项目参与方和受益人，应充分行使自身的权利，为项目提供积极的建议，最大限度地发挥项目的效益。