基于多品种流网络的高铁站站改前后多态理论通过能力对比分析

鲍立群,寇玮华,阚剑锋,许 磊,何宏晖,范 军

(1.中国铁路广州局集团有限公司，广州 510088；2. 西南交通大学 交通运输与物流学院，成都 611756；3. 西南交通大学 综合交通运输智能化国家地方联合工程实验室，成都 611756；4. 西南交通大学 综合交通大数据应用技术国家工程实验室，成都 611756；5. 中铁四局集团公司第五工程公司，江西 九江 332000；6. 中国铁路广州局集团有限公司调度所(施工办)，广州 510088)

针对车站通过能力的研究，主流思路是分别计算咽喉通过能力和到发线通过能力，核定出高铁站通过能力，为解决偏差问题，再用通过能力评估和能力利用率等方法进行修正，但割裂了咽喉与到发线、咽喉与咽喉之间互相关联和互相制约的关系.有些研究将车站通过能力划分层次并对车站通过能力的影响因素进行分析，提出不同层次车站通过能力的计算方法；有些研究根据车站咽喉布局建立到发线运用关系以及按照不同技术作业参数，得出交叉进路条件下接发列车的最优化作业时序，最后提出能力损耗率的概念和计算方法；有的研究为了使综合分析法的计算结果精确化，将一些关键参数取值细致化、标准化；有的研究基于高速铁路车站咽喉区和到发线的相互制约关系，以及车站接发各种类型列车的作业过程与列车进路的关系，结合道岔分组的方法，建立咽喉区和到发线一体化运用的列车进路分配方案优化模型；有些研究尽管将站通过能力分为理论能力、实际和有效能力、可用能力等，但没有把动车组列车对到发线占用时间的差别等因素进行综合考虑[1-5].

尽管针对车站通过能力的研究成果很多，一直没有形成统一的计算方法和更符合现场实际运用的推算模式.在借鉴其他专家学者研究成果基础上，按照高铁站基本布局将站场图抽象为站场网络图，依据动车组列车车流特点，从多品种流网络角度，按照动车组列车车流进出到发线通过咽喉区的不同顺序状态，形成符合行车规则的多态理论通过能力推算模式，利用该推算模式可以针对车站站改前后的通过能力进行纵向横向对比，并分析出车站通过能力变化情况[6-15].

1 符合高铁站站场布局和车流特点的多品种流网络图构建

1.1 多品种流网络结构构建及生成进路数据集

将站场网络图咽喉区分别称为A咽喉区和B咽喉区.设xi、yi分别表示站场图A、B咽喉区进出车站分界点，形成点集X={…,xi,…}及Y={…,yi,…}.设定车站有m条到发线，针对到发线与A、B咽喉区的分界点形成点集A={…,Ai,…}及B={…,Bi,…}.设定vi表示咽喉区道岔，将进出站信号机也视为道岔组，即进出站信号机与进出站方向最外侧道岔之间视为咽喉.针对分界点Ai和Bi分别做作A截面和B截面，到发线区域作一个流汇集的C截面.

将站场图抽象成站场网络图后，在遵从行车组织基础上，基于站场网络图中点线坐标的衔接关系以及行车进路生成规则，构建生成进路数据集Lpass算法，进路数据集构成如表1所列.

表1 进路数据集

为了选择占用咽喉资源尽可能少的进路，将进路数据集中每一个起点至终点之间的进路，按照进路咽喉数量Kj递增排序，再将每条进站进路中的咽喉按照进站顺序排列，每条出站进路中的咽喉按照出站顺序排列.

1.2 站场网络图参数构建

给定时间周期H，默认为24 h，转换为分钟单位周期T=60×H.根据列车运行图、车站股道运用图、高速铁路行车组织细则以及能力查定报告等，查定进路准备时间Δt1、行车间隔Δt2及到发线最大停车间隔时间Δt3.

1.2.1 咽喉区域网络参数构建

针对动车组列车咽喉占用时间主要由进路准备时间、列车通过咽喉时间以及行车时间间隔决定，这三类时间对于通过咽喉区的所有动车组列车没有过大差异，由此可以将每列动车组列车占用咽喉时间简化为相等.根据车站站场工程图纸以及信号设备平面布置图，查定每个咽喉距离，再依据文献[16]查定动车组列车进出站速度，计算动车组列车通过咽喉时间；根据查定的Δt1及Δt2得出咽喉时间占用.取T/tij的整数作为时间周期H内咽喉通过的最大列车数即边的容量，即有公式(1)，同时将以上参数如表2所列，其中如果Δt1<Δt2则Δt=Δt2，否则Δt=Δt1+Δt2.

cij=INT(T/tij).

(1)

基于以上分析，设定咽喉区域网络中边的容量、流量、时间占用为单品种流参数，咽喉区域网络的边如图1所示，其中fij为边(vi,vj)的流量，有0≤fij≤cij.

图1 咽喉区域单品种流参数

1.2.2 到发线区域网络参数构建

鉴于高铁站动车组列车通过咽喉过程以及到发线停留时间的不同，对动车组列车类别归类如表3所列.再根据列车运行图以及车站股道运用图查定到发线停留时间，得出到发线时间占用，将这些参数如表3所列，其中到发线时间占用中的Δt取值按照现场规则取定，即如果Δt1<Δt3，Δt=Δt3，否则Δt=Δt1+Δt3.

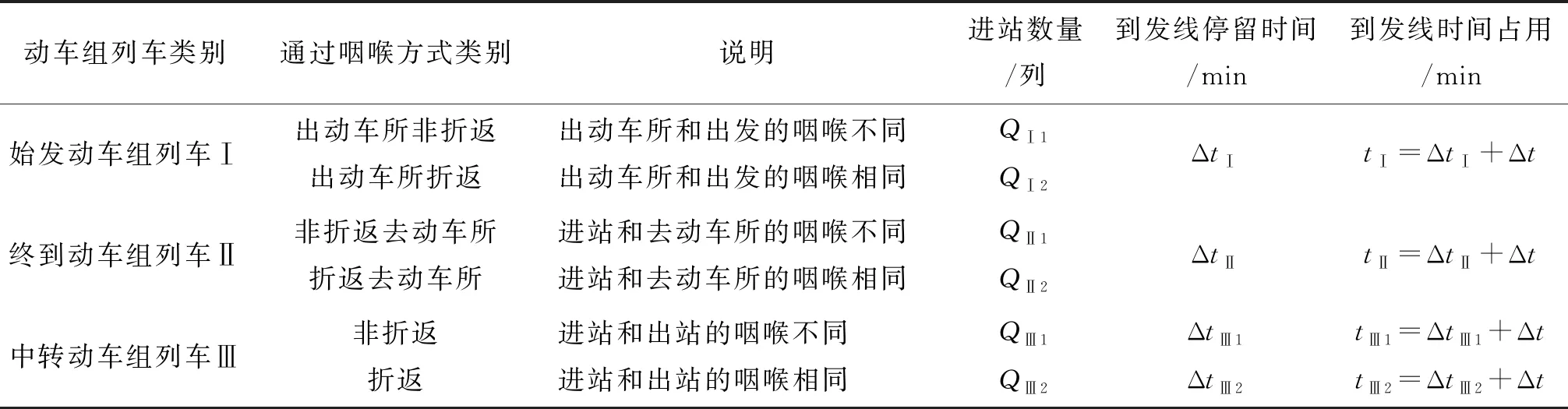
表3 动车组列车运行方式归类及相关参数

为了表述方便，本文将表3中通过咽喉方式类别称为6类动车组列车，即网络图有6种品种流.

1) 单条到发线参数确定

针对到发线节点Ai和节点Bi之间的线路，设定fⅠ1、fⅠ2、fⅡ1、fⅡ2、fⅢ1、fⅢ2分别表示6类动车组列车数量，cij表示该到发线最大能力，在时间周期T内可有fⅠ1×tI+fⅠ2×tI+fⅡ1×tⅡ+fⅡ2×tⅡ+fⅢ1×tⅢ1+fⅢ2×tⅢ2≤T以及fⅠ1+fⅠ2+fⅡ1+fⅡ2+fⅢ1+fⅢ2≤cij.由于查定的时间占用为最低限，实际行车组织中这些时间会高于查定的时间占用，另外，防止6类动车组列车在能力组合时发生数值“溢出”，采用6类动车组列车的最大到发线时间占用做为计算基准即有公式(2).

tAB=max{tⅠ,tⅡ,tⅢ1,tⅢ2},

(2)

时间周期T内单条到发线接收列车能力cAB取T/tAB的整数，即有公式(3).

cAB=INT(T/tAB).

(3)

基于以上分析，针对网络节点Ai和Bi之间对应的到发线设定边的参数为复合参数，其中三组参数依次表示到发线能力、6类动车组列车量及对应的时间占用，取值均为正整数或0，如图2所示.

图2 到发线区域多品种流复合参数

2) 所有到发线参数确定

本研究不涉及单条到发线行车方案，即不考虑公式fⅠ1×tⅠ+fⅠ2×tⅠ+fⅡ1×tⅡ+fⅡ2×tⅡ+fⅢ1×tⅢ1+fⅢ2×tⅢ2≤T中6类动车组列车数量.在遵从咽喉与到发线、咽喉与咽喉之间互相关联和制约关系以及行车进路生成规则基础上，基于公式(1)确定的咽喉能力以及公式(2)确定的单条到发线能力限制，确定最多能有多少动车组列车进出所有到发线，所以可以从A截面、B截面、C截面的角度研究车站理论通过能力问题.

A截面接收的最大流量有公式(4)：

(4)

式中：f(Ai)表示第i条到发线节点Ai接收的最大流量；QA表示A截面接收的最大流量.

B截面接收的最大流量QB则有公式(5)：

(5)

式中：f(Bi)表示第i条到发线节点Bi接收的最大流量；QB表示B截面接收的最大流量.

针对整个到发线C截面接收的最大流量QC则有公式(6)：

QC=QA+QB.

(6)

由此可知QC即为高铁枢纽车站的理论通过能力，结合表3归类的6类动车组列车可有公式(7)：

QⅠ1+QⅠ2+QⅡ1+QⅡ2+QⅢ1+QⅢ2=QC.

(7)

鉴于网络图流预推是在不考虑流分布状态下，基于网络流理论推算网络图能够通过的最大流是多少即确定网络图能力，由此本文采用流预推方法推算公式(4)及公式(5)的f(Ai)和f(Bi)值.

2 网络图最大流推算的流预推过程

列车进出到发线通过咽喉区的顺序不同，将会导致咽喉以及车站的通过能力结果不尽相同.尽管通过咽喉区顺序不同，但必须保证“有进才有出，有出必有进”的行车原则、进入到发线进路流量、到发线剩余能力及流出到发线进路流量三者之间平衡的原则、交叉进路中共用咽喉进出流量“相互制衡”的原则.8种进出到发线咽喉先后顺序的不同状态如表4所列.

表4 进出到发线的咽喉先后顺序状态

2.1 参数查定及初始化过程

1) 根据第1.2节咽喉区域网络参数的约定，查定距离参数和时间参数，计算通过咽喉时间Δtij，再利用公式(1)计算咽喉区域边的容量cij值，设定流量初始值fij=0，形成表2内容的数据集.

2) 根据第1.2节到发线区域网络参数的约定，查定6类动车组列车的时间参数并计算出到发线时间占用，形成表3内容的数据集.利用公式(2)选取计算基准，利用公式(3)计算单条到发线接收列车数最大能力cAB值，再针对到发线设定c[i]=cAB，流量初始值f[i]=0，其中i=1,…,m.

3) 设定流进入到发线进路的流量调整量为lc，流出到发线进路的流量调整量为lg.如果流进入到发线进路与流出到发线进路为交叉进路，设定lp为交叉进路中所有共用咽喉的最小剩余能力.再设定流进入到发线进路与流出到发线进路的最终调整量为lq.

4) 设定通过A咽喉流入A截面的流量总量为QA，其中通过A咽喉流出到发线的量为QAA，通过B咽喉流出到发线的量为QAB.设定通过B咽喉流入B截面的流量总量为QB，其中通过A咽喉流出到发线的量为QBA，通过B咽喉流出到发线的量为QBB.通过A咽喉流入A截面但无法流出的量为QAD，通过B咽喉流入B截面但无法流出的量为QBD.

2.2 流量预推过程

尽管行车中涉及到进路之间交叉以及敌对进路等现象，但在能力计算上均体现为“能力消耗”，另外，流预推时流入到发线的流同时又从同一个咽喉区流出，会出现“能力对冲”问题，所以算法中需要建立 “能力消耗”以及“能力对冲”相对应的推算公式.鉴于表4每种状态的流预推过程相同，本文以“A咽喉优先进到发线”的“A咽喉进A咽喉出B咽喉出+ B咽喉进A咽喉出B咽喉出”为例说明流预推算法过程.

算法2.1“A咽喉进A咽喉出B咽喉出” 流预推算法

1) 如果A咽喉存在还没有被选定过的进站方向点xi，选定该点作为进站进路起点，否则转到“B咽喉进A咽喉出B咽喉出”的子过程.

2) 如果存在c[i]-f[i]>0的到发线，选定Ai作为进站进路终点，否则转到第(1)步.

3) 按照行车进路规则，推断xi和Ai之间的进站进路，如果不存在进路，转到第(2)步.

4) 根据第(3)步推断的进站进路，针对该进路中所有边选择lc=min{…,cij-fij,…}.如果lc=0，转到第(2)步，否则使lq=min{lc,c[i]-f[i]}.

5) 如果A咽喉存在还没有被选定过的出站方向点xi，选定该点作为出站进路终点，否则转到第(11)步.

6) 按照行车进路规则，推断Ai和xi之间的出站进路，如果不存在进路，转到第(5)步.

7) 根据第(6)步推断的出站进路，针对该进路中所有边选择lg=min{…,cij-fij,…}，如果lg=0，转到第(5)步.

8) 根据第(3)步推断的进站进路和第(6)步推断的出站进路，判定两个进路是否为交叉进路.如果不是交叉进路，使lq=min{lq,lg}；如果是交叉进路，针对两条进路中所有的共用咽喉选取最小的剩余能力lp=min{…,cij-fij,…}，使lq=min{lq,INT(lp/2)}.

9) 针对进站进路、出站进路中所有咽喉以及第i个到发线进行流量调整，即所有咽喉流量调整为fij=fij+lq和第i个到发线流量调整为f[i]=f[i]+lq.通过A咽喉流入A截面流量总量QA=QA+lq，其中通过A咽喉流出到发线的量QAA=QAA+lq.

10) 如果存在lc-lq>0，转到第(5)步，否则转到第(1)步.

11) 如果B咽喉存在还没有被选定过的出站方向点yi，选定该点作为出站进路终点，否则转到第(1)步.

12) 按照行车进路生成规则，推断Ai和yi之间的出站进路，如果不存在进路转到第(11)步.

13) 根据第(12)步推断的出站进路，针对该进路中所有边选择lg=min{…,cij-fij,…}，如果lg=0，转到第(11)步，否则使lq=min{lq,lg}.

14) 针对进站进路、出站进路中所有咽喉以及第i个到发线进行流量调整，即所有咽喉流量调整为fij=fij+lq和第i个到发线流量调整为f[i]=f[i]+lq.通过A咽喉流入A截面流量总量QA=QA+lq，其中通过B咽喉流出到发线的量QAB=QAB+lq.

15) 如果仍然存在lc-lq>0，转到第(11)步，否则转到第(1)步.

算法2.2“B咽喉进A咽喉出B咽喉出” 流预推算法

该过程和上一过程思路相同，鉴于篇幅所限不再赘述.最后同样得出通过B咽喉流入B截面流量总量QB，其中通过A咽喉流出到发线的量QBA，通过B咽喉流出到发线的量QBB.

利用两个算法进行流预推有可能出现剩余进站能力，即通过上一过程推算后，存在通过进站进路可以流入到发线但无法流出的能力.推断进路以及确定进路流量的思路和上一过程相同，差别是不再寻找出站进路，最后可以得出通过A咽喉只能流入A截面的量QAD，通过B咽喉只能流入B截面的量QBD.

鉴于本文研究内容的人工计算量大以及计算过程复杂等原因，基于研究思路和研究方法开发了《高铁站通过能力计算及行车组织优化系统》，利用该系统进行推算、计算数据的同时，也可以验证本文研究思路和研究方法是否具有可行性.

3 深圳北站站改前后理论通过能力推算分析

深圳北站是具有一定规模的高铁枢纽站，有m=20条到发线和具有动A线和动B线的1个动车所，北咽喉有广州方向，南咽喉有厦门和香港方向，针对深圳北站站场图构建A截面、B截面、C截面，站改前站场图抽象成站场网络图的示意图如图3所示.

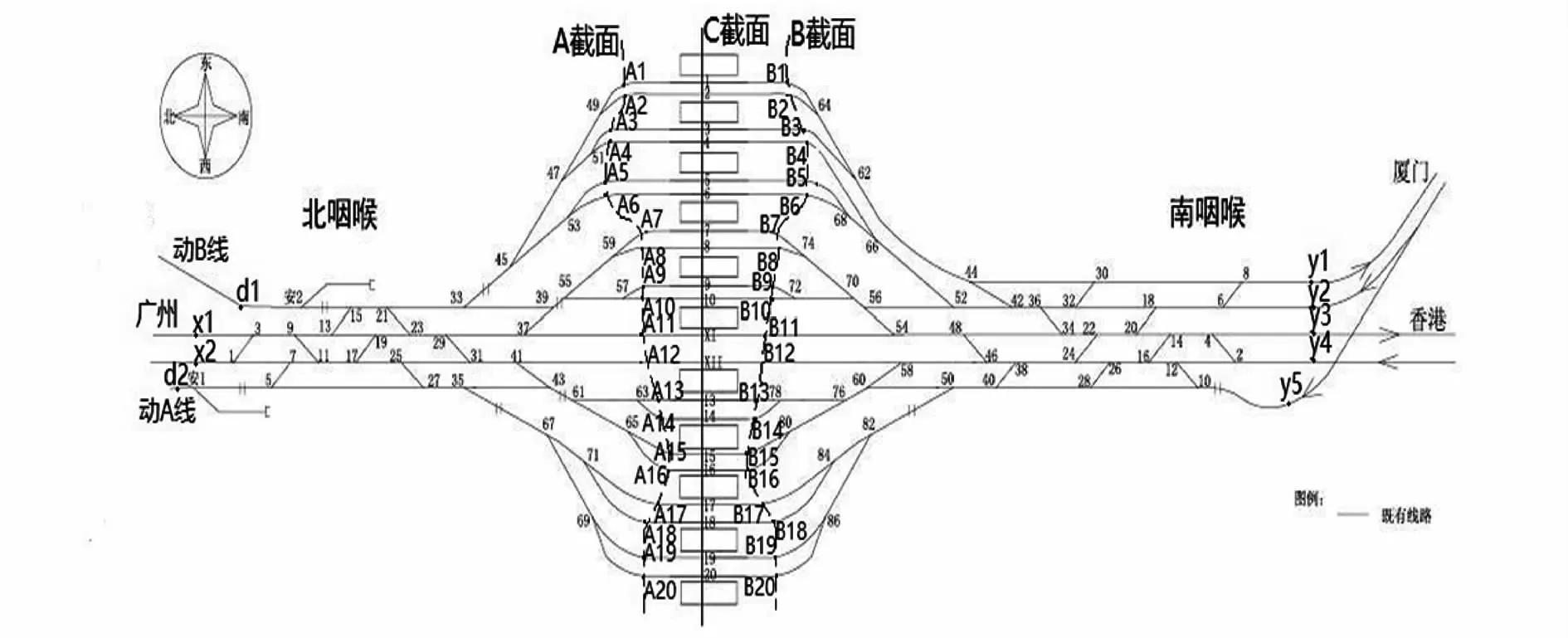
图3 构建A、B、C截面的深圳北站站改前站场图

3.1 时间占用参数确定及咽喉能力推算

将天窗时间以及深圳北站运行图的最早最晚接发车时间结合起来综合考虑，这里取H=18 h，即有T=60×18=1 080 min.为了提高接发能力，深圳北站于2019年11月开始进行赣深方向新线引入以及第二动车所的建设.以站改后站场图抽象为网络图为例的咽喉能力计算结果如图4所示.

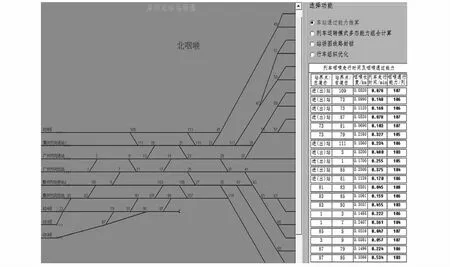
图4 深圳北站站改后站场网络图及咽喉能力

查定规定进出站车速v=40 km/h及每个咽喉距离lij，得出动车组列车的行驶时间Δtij=l/v×60 min.查定的进路准备时间Δt1=5 min、列车行车间隔Δt2=5 min、到发线停车间隔Δt3=8 min，可以得出数据集如表5所列.

表5 深圳北站动车到发线时间占用参数

3.2 深圳北站理论通过能力推算

利用《高铁站通过能力计算及行车组织优化系统》中基于本文研究思路和方法形成的功能，针对深圳北站站改前及站改后分别推算出表4所示8种多态理论通过能力，多态理论通过能力结果分别如图5～6所示，分布状态分别如图7～8所示.对比可以看出数据分布非“极端”的才符合行车组织可行情况.另外，站改前后通过能力数据分布合理与否，二者之间的同一种状态都互相对应.

图5 站改前多态理论通过能力推算结果

图6 站改后多态理论通过能力推算结果

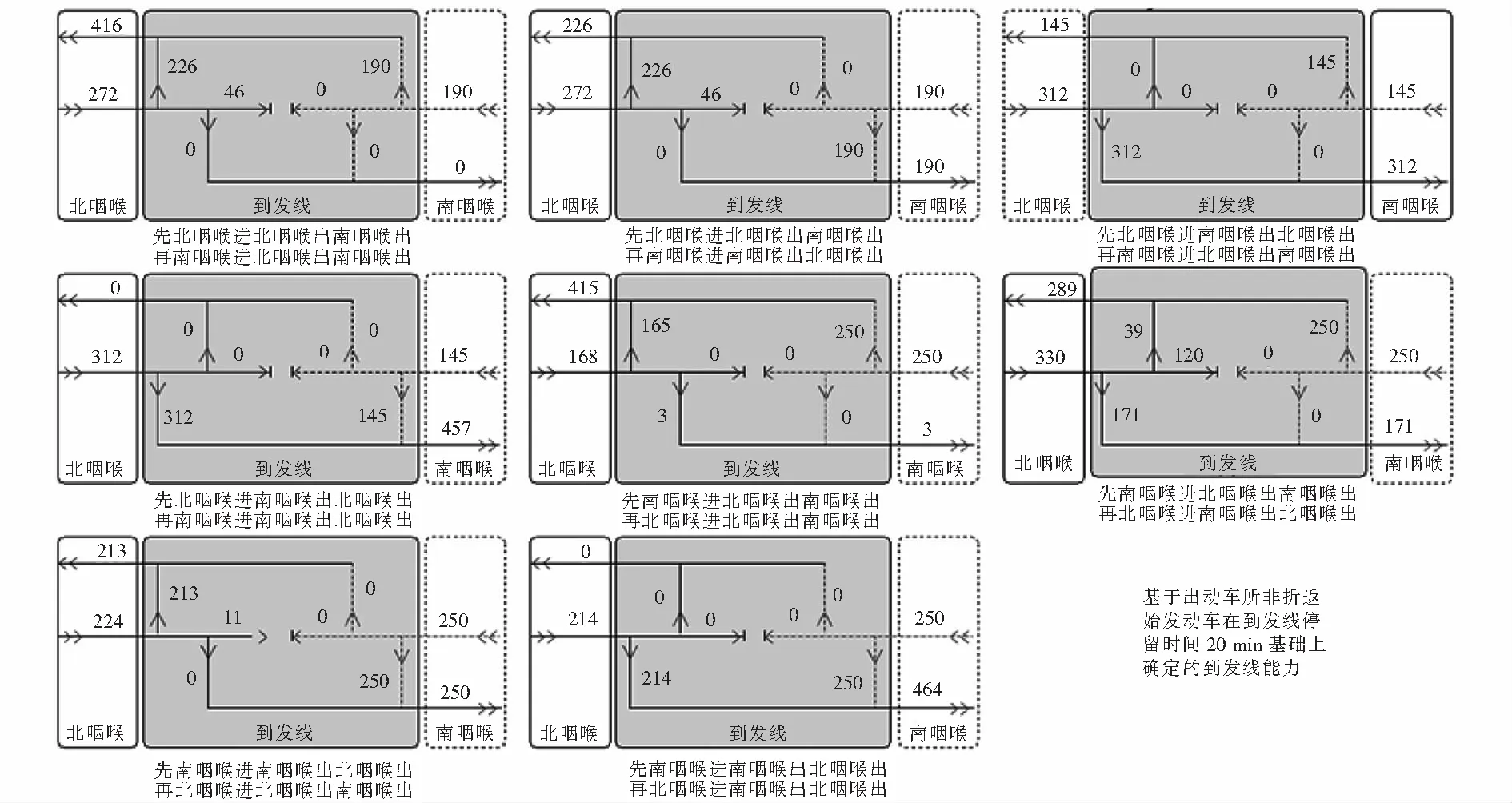
图7 深圳北站站改前多态理论通过能力分布状态(单位:列)

3.3 深圳北站站改期间通过能力影响分析

深圳北站站改主要对站场北咽喉进行，南咽喉的站场布局与站改前大致相同，所以车站站改通过能力变化主要由北咽喉引起.北咽喉站改后原有广州方向行车线不变，增加赣州方向三条行车线，同时增加深圳第二动车所，这将导致北咽喉通过能力增加，也必然会导致车站通过能力增加，由于咽喉区与咽喉区之间通行能力的互相关联和互相制约关系，也会导致南咽喉通过能力发生变化.

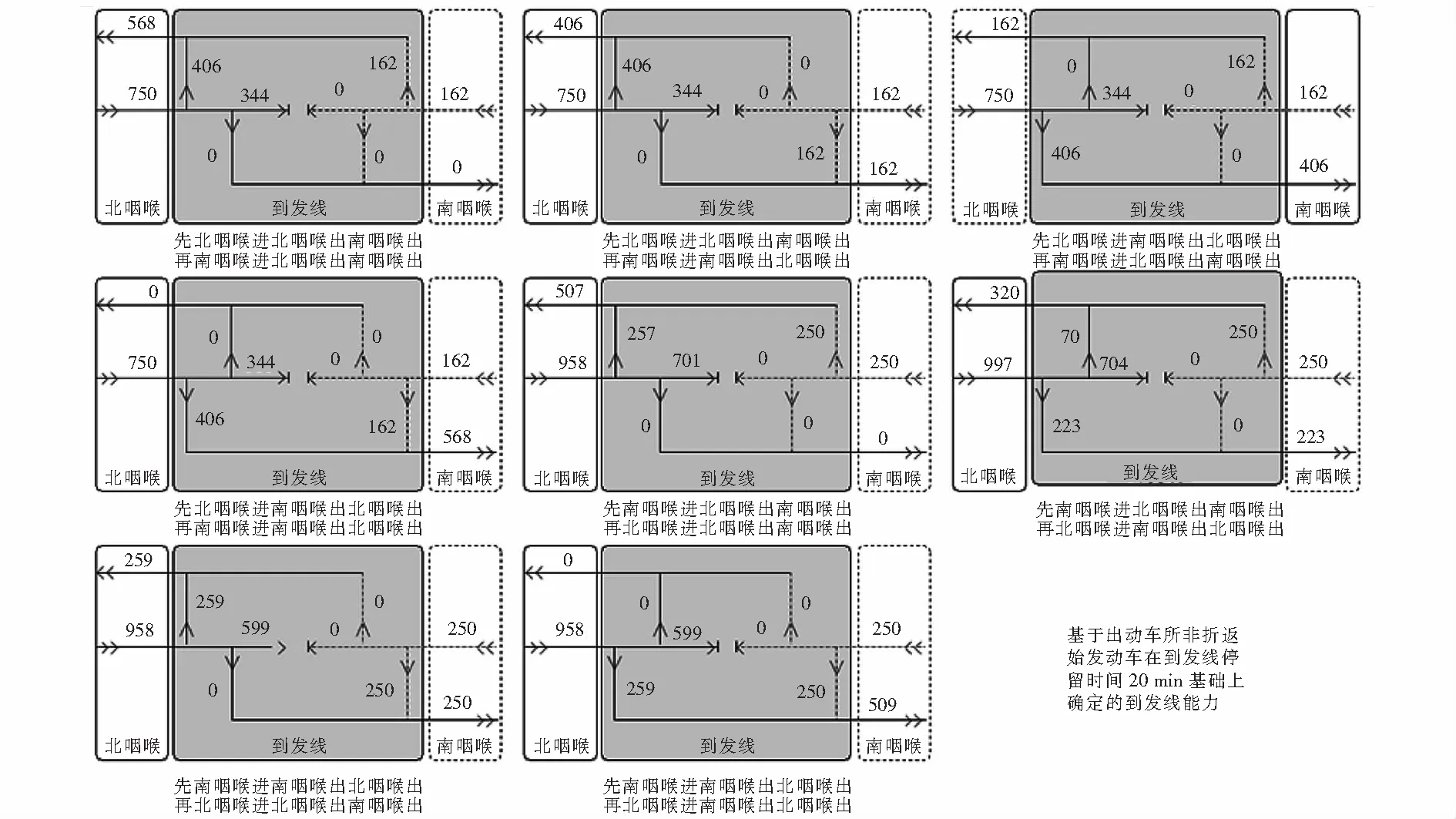
图8 深圳北站站改后多态理论通过能力分布状态(单位:列)

咽喉进站能力和出站能力的大小决定了咽喉和车站通过能力的大小，但数据 “极端分布”和“极端不均衡”状态不属于车站行车常态，本文根据图5～8选取4种数据分布“非极端相对均衡”的状态进行站改前后通过能力对比分析，将4种状态分别记作A、B、C、D状态，如表6所列.

表6 深圳北站站改前后通过能力对比

针对以上4种可行状态的通过能力分析总结如下：

1) 站改前每种状态的车站通过能力受限于咽喉通过能力，但站改后每种状态的车站通过能力受限于到发线接发能力，这也为未来车站通过能力的扩展提供了方向.

2) 站改前每种状态的车站通过能力变动幅度比较小，站改后有2种状态的咽喉通过能力变动幅度较大，其余两种状态的咽喉通过能力变化幅度较小.

3) 站改前车站通过能力最低为416对，最高为463对，范围相差463-416=47对，但有3种状态的通过能力都集中在460对附近，可以推断深圳北站站改前通过能力约为460对.

4) 站改后车站通过能力分两种情况，北咽喉区优先顺序时，有两种状态为568对，结果相同，可以推断通过能力大约为568对；南咽喉区优先顺序时，通过能力最高为543对，最低为509对.

5) 针对同一种状态下，站改后北咽喉通过能力的变化量以及变化程度，较站改前的差异变化较大，南咽喉变化较小.

6) 站改后北咽喉区优先顺序时，咽喉通过能力和车站通过能力增加幅度都在24%以上，甚至A状态下达到了79%；南咽喉区优先顺序时，车站通过能力增幅保持在20%以下.

7) 站改后的A状态下，南咽喉的通过能力没有增加反而减小，是因为受到发线能力的影响，北咽喉站改后通过能力大幅度增加，由北咽喉优先进入占用了较多到发线资源，从而使得南咽喉的通过能力减小.

4 结论

利用多品种流网络理论首创性地研究了车站站改前后通过能力对比分析，为相关研究提供了一种全新的研究视角，可以为站改方案评估以及行车组织优化等提供可靠实用的依据和决策上的支撑，也可以针对不同的站改方案，比选出可行、满意的方案.