豫西丘陵地带黄土介质水动力弥散特性试验研究

卜新峰，万伟锋

（黄河勘测规划设计研究院有限公司，郑州 450003）

0 引 言

弥散作用对污染质在含水介质中的运移具有显著的影响，在岩性较细地层、弱透水层或包气带地下水污染质运移模拟过程中，弥散参数的研究是地下水溶质运移模拟的关键环节［1，2］。

弥散系数是一个与流速以及多孔介质自身特性有关的张量，具有方向性［3］。弥散度反映空隙介质骨架结构的特征长度，对于均匀介质，弥散度是一个常数，而天然含水层中由于微层理、细裂隙、地层透镜体的存在以及局部沉积韵律的变化，使得弥散度根据试验尺度的差异，呈现出不同的变化［3］。弥散试验是获取弥散参数以及揭示地下水中溶质运移机理较为可靠的方法，同时是研究污染物在地下水中运移重要的环节［4］。

根据试验场所的区别，弥散试验分为室内和野外两大类。室内弥散试验方法主要有垂直土柱法、水平土柱法和水特征曲线计算法等［5］。常用的野外弥散试验方法有单井法，多井法和单井地球物理法，其中尤以多井法试验结果可靠性较好［6］。目前，学术界普遍认为，对比室内试验，野外弥散试验得到的弥散度值一般超出几个数量级，且野外弥散试验得到的弥散度值也随着野外试验尺度的增大而增大，并随溶质运移时间而增大［7-9］，显然这一规律对于均质各向同性的岩土体是适合的，对于非均质岩土体，室内试验与野外弥散试验结果的关系较为复杂。黄康乐等［10］在室内开展了一维均质和非均质溶质运移实验，得到了弥散度随土柱长度变长而增大的结论。陈静等［11］学者的研究表明，弥散系数与含水介质的非均匀程度显著相关，即在尺度相近的前提下，均质土柱的弥散系数小于非均质土柱，二者最大值的差值达一个数量级。

对于室内试验显著小于野外弥散试验这样一个现象，大部分学者均以尺度效应去阐述其机理，对于部分室内试验结果与野外弥散试验结果相近或者偏大的现象，多归因于试验的可信度差导致。对于非均质性因素对室内试验的影响程度、非均质性影响下室内试验结果与野外试验结果的对比分析则研究较少。

本文以豫西丘陵地带黄土地层为研究对象，针对其包气带地层厚度大，地下水埋深大，垂向发育的微节理、微裂隙等大孔隙使其具有显著的非均质性等特征，结合室内和野外弥散试验，在某试验场地开展了基于两种尺度的黄土介质弥散特性试验研究，进而讨论了黄土介质的空间非均质性对其弥散能力的影响，试验获取的水动力弥散参数可为本地区相似工程场地弥散参数的取值以及地下水污染预测提供一定的经验借鉴和数据支撑。

1 试验场地基本条件

野外弥散试验的场地选择位于三门峡西南部的某场地一和场地二，两处试验场地均处于豫西黄土塬区，地层基本一致，地下水类型主要为孔隙水、孔隙裂隙水。浅部含水层岩性以中、下更新统黄土（含裂隙）及黄土夹钙质结核层为主，富水性差。两处场地对应的典型试验点浅表地层岩性分布情况如图1所示。

野外现场弥散试验共进行4 组，分别为场地一的KM-01孔、KM-03 孔弥散试验和场地二的KM-02 孔、KM-04 孔弥散试验，两处试验场直线距离约为2 km。场地一典型试验点浅层地下水位埋深达156 m；场地二典型试验点浅层地下水位埋深为72 m。为了获取地层的渗透系数，首先开展了现场抽水试验，试验井孔在地下水位以下均设置花管进水管，获取多层地层的综合渗透系数（相当于地层渗透系数的加权平均值）。根据抽水试验计算结果，场地一和场地二浅层含水层的综合渗透系数分别为0.19 m/d和0.23 m/d。

2 试验方法及参数计算

2.1 野外原位弥散试验方法及参数计算

2.1.1 野外原位弥散试验

由于试验场地浅部地层岩性以粉土为主，渗透系数较小，地下水天然渗透流速较慢，野外弥散试验采用人工干扰流场（径向收敛流弥散试验），即以抽水孔为接收孔，以观测孔为投源孔，利用小降深稳定抽水条件下的流场开展野外原位弥散试验。即在抽水试验某一落程的稳定阶段，当流量和水位达到相对稳定时，首先测定抽水孔水样中的Cl-背景值（试验场地下水中氯离子背景值为12.62 mg/L），然后将50 kg 固态NaCl 完全溶解后一次性注入观测孔中，定时在抽水孔中采取水样进行现场滴定实验，确定水样中Cl-浓度变化情况，绘制浓度变化曲线，计算弥散系数，含水层孔隙度参数采用钻孔原状土样室内试验结果。

野外试验用NaCl 作为示踪剂是由于氯化钠具有很好的溶解性，在饱和状态下，几乎不与含水层中的物质发生化学反应，对周边地下水环境基本不造成影响；同时地下水中氯离子背景值浓度较低，示踪剂的注入容易引起氯离子的显著变化。

2.1.2 弥散参数计算方法

当在管井中开展抽水时，井附近的天然流速与抽水引发的流速相比几乎可以忽略不计，在一定的假设条件下建立径向收敛流场瞬时注入法的数学模型，描述稳定的径向渗流场溶质运移二维对流弥散方程为［12-14］：

其定解条件为：C（r，0）=0r≥0，t=0

式中：aL为纵向弥散度，m；aT为横向弥散度，m；u为平均孔隙流速，m/d；C0为示踪剂浓度，mg/L；θ为方位角，°；Q为抽水量（或注水量），m3/d，对注水井（散发流）Q＞0，对抽水井（收敛流）Q＜0；r为投源孔与观测孔的距离，m；为投源孔与观测孔之间含水层的平均厚度，m；n为含水层有效孔隙率。式（1）适用于径向散发流（u＞0）和径向收敛流（u＜0）。

试验不考虑地层以及钻孔结构对NaCl 的吸附和其他物理化学反应，对流—弥散方程的最后一项是由于横向弥散产生的，对径向收敛或径向散发的渗流场，由于径向流速显著大于其他方向的流速，故可以忽略横向弥散作用产生的影响，式（1）可以进一步简化为：

对于瞬时注入径向流的情况，目前尚无解析解，通过（2）式，法国学者J．P．Sauty 采用有限差分的数值法进行参数计算，求得以Peclet数P为参数，以无因次浓度Cr和无因次时间tr（或lgtr）分别为纵横坐标的标准曲线，用以确定含水层的纵向弥散度aL。

2.2 室内一维土柱淋滤试验方法

2.2.1 一维土柱试验

室内试验采用如下的试验装置，主要包括土柱、马氏瓶和渗滤液收集瓶等组成，见图2。

试验采用常水头入渗的形式进行，即在试验过程中保持各土柱的水头差不变。供试土样取自两处试验场地之间的某典型剖面，土柱1 为原状土样，土柱2 为室内人工装填的扰动样（可视为均质各向同性介质），两组土样均取自地表以下5.0 m范围以内，为了均匀布水和过滤，各土柱上、下均装置了厚为5 cm 的石英砂，进水口设置在土柱的下部，实验控制条件见表1。

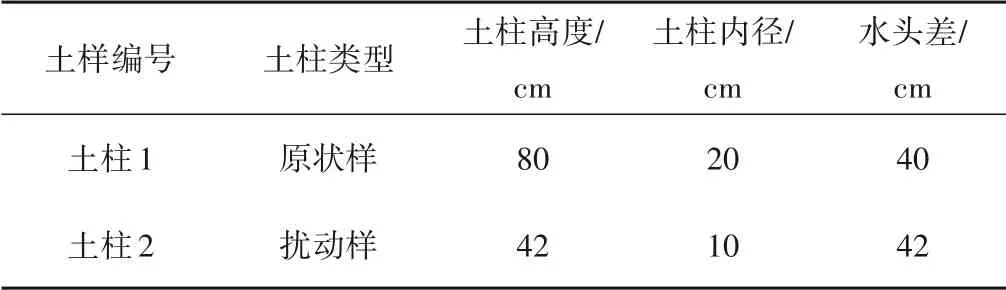
表1 土柱淋滤试验基本控制条件［15］Tab.1 Basic control conditions of soil column leaching tests

试验先将自来水（Cl-含量3.67 mg/L）从土柱底部缓慢湿润土柱，待土柱完全饱和后，记录渗透速度，以确定试验的取样时间间隔，稳定一段时间后将自来水改为注入一定浓度的碘化钾溶液，按确定的时间间隔取样，测定渗出液中碘离子的浓度［15］，进而绘制碘离子浓度随时间变化的曲线，即穿透曲线。

2.2.2 一维饱和土柱弥散参数计算方法

一维饱和土柱弥散试验的边界条件相对简单，物理概念清晰，尤以通过该试验获取的溶质穿透曲线可反映不同溶质在不同的多孔介质中混合置换和溶质运移特性而得到广泛的认可和应用［16，17］，通过易混合置换试验测得碘离子的穿透曲线，利用稳态水流一维垂直饱和土柱控制方程的解析解，可方便直观地求取饱和土柱水动力弥散系数和纵向弥散度。根据室内测得的碘离子穿透曲线，利用相关推导公式（4）计算弥散系数［3］。

稳态水流一维垂直饱和土柱的控制方程为典型的一维对流—弥散方程：

其定解条件为：C（x，0）=0r≥0，t=0

式中：DL为弥散系数，m2/d；u为平均孔隙流速，m/d；x为示踪剂运移距离，m。

对式（4）进行拉普拉斯变换并进一步简化表达可得DL的计算公式为：

式中：t0.16、t0.5、t0.84分别为相对质量浓度C/C0达到0.16、0.5 和0.84的时间，d。

根据公式（6）计算平均孔隙迁移速率：

式中：L为土柱高度（入水口到出水口距离），m。

3 结果分析与讨论

表2给出了4 组野外弥散试验点和两组土柱淋滤试验的基本条件以及弥散参数计算结果。KM01～KM04 四个试验点的野外试验尺度在3.0～6.4 m 之间；而对比表1，室内土柱淋滤试验的试验尺度为42和80 cm。

表2 弥散试验计算成果表Tab.2 Calculation results of dispersion tests

试验结果分析与讨论：

3.1 野外原位弥散试验

根据四组野外弥散试验计算结果，KM01～KM04 获取的纵向弥散度aL在0.25～0.32 m 之间，平均值为0.28 m；代表场地水平方向的纵向弥散系数DL在0.03～0.12 m2/d 之间，平均值为0.07 m2/d。整体而言，纵向弥散度数值差异较小，具有很好的稳定性，能够客观地反映试验尺度条件下含水层空隙介质的性质，可信度较高；而纵向弥散系数数值具有一定的离散性，最大值是最小值的4倍，但都在一个数量级上。

分析野外弥散试验计算结果出现差异的原因，在场地试验条件相近、试验手段和参数计算方法相同的情况下，其纵向弥散度数值呈现出较好的稳定性，符合多孔介质水动力弥散理论的一般规律；弥散系数的差异主要与试验孔间距和平均孔隙流速有关。由于场地野外试验尺度差异较小，在不考虑尺度效应微小差异的前提下，场地水平方向的纵向弥散系数主要与平均孔隙流速有关，通过回归分析表明，两者之间呈线性关系，即DL=0.255 6u+0.006 7，R2=0.976 4，平均孔隙流速越大，弥散系数也随之增大。试验结果与王飞以及翟春生等人的室内试验研究结论呈现出较好的一致性［19，20］。

3.2 室内土柱试验

根据室内土柱试验计算结果，土柱1 与土柱2 淋滤试验获取的纵向弥散度aL在0.18～1.20 m 之间，代表场地垂直方向的纵向弥散系数DL在0.07～2.16 m2/d 之间。根据土柱淋滤试验的计算结果，土柱1 原状土柱与土柱2 人工装填土柱之间纵向弥散度与弥散系数均差异显著，纵向弥散度之间的比值达到6.67，弥散系数之间的比值超过了30.8，差值达到了一个数量级的水平，即土柱1 原状土柱的弥散参数显著大于土柱2 人工装填土柱。计算结果与陈静、黄康乐等学者的研究成果具有较好的一致性。

由表1、2 中的试验数据可知，土柱1 的长度接近土柱2 的2倍，孔隙度达土柱2 的2.5 倍。在水力梯度相近的情况下，弥散参数之间产生显著差异的主要原因与土柱的非均匀程度以及土柱长度等因素密切相关。在原状的非均质土柱中，孔隙分布的离散性会造成水力传导度的空间差异，进而影响介质的弥散能力。分析认为，室内土柱试验计算所得弥散参数之间产生显著差异的主要原因与土柱的非均匀程度密切相关，其次是土柱长度。

此外，土壤中的水分总是向土水势降低的方向移动，黄土介质垂向上发育的大孔隙以其较小的土水势使得水流优先从大孔隙中通过，加上土壤中的大孔隙对水分运动的阻力非常小，所以其运动速度非常快，这就导致了存在大孔隙的土柱1原状土柱的平均孔隙流速远大于土柱2 扰动土柱，约为扰动土柱的4.7 倍。在水流运动的同时，溶质也随着水分的运移而快递扩大其运移范围。这种渗透流速对渗透系数产生的影响与试验场地野外试验结果具有一定的相似性。

因此，土柱1原状土柱获取的弥散参数更能代表野外实际，黄土介质垂向上发育的微节理、微裂隙等大孔隙是造成黄土介质垂向弥散能力较大的重要原因，其对黄土介质垂直方向水动力弥散系数的影响要超过孔隙的非均匀程度和土柱高度。

3.3 对比分析

通过对比室内和野外现场弥散试验结果，在不考虑重力影响以及尺度效应的前提下，土柱1 原状土柱纵向弥散度aL达1.20 m，是本次野外试验纵向弥散度最大值的3.75倍，而弥散系数值DL达2.16 m2/d，是野外试验弥散系数最大值的18倍。显然这两种试验结果的显著差异主要源于黄土介质的空间非均质性，室内试验结果代表的是黄土介质垂向弥散能力，而野外弥散试验获取的是黄土介质水平方向的弥散能力。因此，不能简单地再以试验结果进行大小的对比。当研究对象为显著的非均质性岩土体时，应特别重视不同方向弥散能力的试验研究，当场地条件合适时，可以采取相近尺度的室内试验和野外试验进行对比，如场地条件不易实现垂向原位弥散试验，则宜开展室内二维水动力弥散试验，或者利用室内试验同时结合野外试验获取场地的弥散参数。

4 结 论

（1）基于径向收敛流瞬时注入法的场地野外弥散试验，获取的纵向弥散度aL在0.25～0.32 m 之间，代表场地水平方向的纵向弥散系数DL在0.03～0.12 m2/d 之间，在试验尺度相近的前提下，场地水平方向的纵向弥散系数主要与平均孔隙流速有关，两者之间显示了很好的线性关系，即平均孔隙流速越大，弥散系数也随之增大。

（2）室内土柱试验获取的土柱1 原状土柱的纵向弥散度aL为1.20 m，代表场地垂直方向的弥散系数值DL为2.16 m2/d，两者的计算值远大于土柱2。分析认为，土柱1 原状土柱获取的弥散参数更能代表野外实际，黄土介质垂向上发育的微节理、微裂隙等大孔隙是造成黄土介质垂向弥散能力较大的重要原因，其对黄土介质垂直方向水动力弥散系数的影响要超过孔隙的非均匀程度和土柱高度。

（3）室内土柱淋滤试验获取的弥散参数显著大于野外现场弥散试验，二者获取的纵向弥散度比值为3.75，黄土介质的空间非均质性在水平和垂直方向的显著差异影响其水动力弥散能力，即黄土介质的垂向弥散能力显著大于水平方向。本次土柱1原状土柱试验结果可为该地区相似工程场地垂直方向弥散参数的取值提供参考和经验借鉴。

（4）对于豫西丘陵地带的黄土介质，径向收敛流瞬时注入法弥散试验在含水层水平方向上的弥散参数获取具有良好的适用性，便于在野外开展和推广。而对于试验场地垂直方向弥散参数的获取，如进行室内土柱淋滤试验，宜采用原状土柱进行。□