气敏材料表征的悬臂梁微称重温控系统设计

陆天海，费 超，徐大诚，于海涛

(1.苏州大学微纳传感技术研究中心，江苏苏州 215006;2.中国科学院上海微系统与信息技术研究所，传感技术国家重点实验室，上海 200050)

0 引言

随着对气敏材料研究的进一步深入，新型气敏材料的敏感性能表征显得越发重要。近几年，以MEMS技术为核心的谐振式微悬臂梁凭借集成化、小体积、高灵敏度、低噪声、实时性、低功耗等优势，逐渐成为气体分子吸脱附实验中的重要角色[1-2]。该方法将吸附在微悬臂梁上的气体分子质量的改变转变为其谐振频率的改变，再利用悬臂梁谐振频率的变化定量计算出实验中吸附功能材料的热力学、动力学参数[3]。由于气体分子吸脱附实验需要稳定的温度环境，定量计算需要精确的温度参数，因此温度控制的精确性及稳定性显得尤为关键。同时，较低的温度环境可以增加气体分子的吸附量，从而增大悬臂梁谐振频率变化量，提高整个系统的信噪比，在更宽温度范围评估气敏材料性能。

气敏材料吸脱附性能研究中大多使用ASAP 2020(Micromeritics，USA)[4]、STA 449(Netzsch，Germany)[5]、HWS-225L(北京时代新天测控技术，中国)等温控设备。这些温控仪器中加热与制冷系统常分开制作，导致设备体积增加、制作复杂度增加、功耗增加等。其中加热主要使用电加热和电阻丝加热，制冷主要使用循环水制冷、液氮制冷和压缩机制冷等方法。循环水制冷可达到的温度有限，并且制冷速度较慢；液氮制冷速度快，但是功耗大、成本高、运输困难、危险性高、低温不易控制；压缩机制冷功耗较高、噪音大等缺点无法避免[6]。

为解决传统加热制冷方法体积大、能效比低，控温精度低、升降温速度慢等问题，同时制作适用于微悬臂梁气敏材料表征实验的小体积、精确快速控温、宽温控范围的温控仪器，本文在分析相关文献的基础上，提出了将半导体制冷技术应用于悬臂梁气敏材料性能表征的温控系统。该系统由帕尔贴、测温电路、驱动电路、MCU系统组成。通过双层帕尔贴结构拓宽温控范围，提高升降温速率；采用基于DRV595的PWM驱动电路实现帕尔贴控制；设计基于Pt100的高精度自校准温度测量电路；温度控制采用Fuzzy-PID算法，提升了温度控制性能，同时解决了帕尔贴系统数学模型随温度发生改变的难题，为研制小型化、高精度和高能效比的气敏材料分析仪器提供了一条有效途径。

1 气敏材料性能表征

利用微悬臂梁进行微称重时，在悬臂梁上涂抹气敏材料，在T1和T2温度下分别对气体分压为p1和p2的气体进行吸附实验，并计算得到焓变ΔH数学表达式如(1)所示[7]：

(1)

式中R为气体常数。

假设实验中由于温度波动或温度偏差大导致真实温度值为T1+ΔT1和T2+ΔT2，则焓变计算变为式(2)：

(2)

温度误差或波动在不同的温度点处的最大值多相近，因此考虑ΔT1≈ΔT2，则有式(3)：

(3)

根据实验环境温度稳定性的不同，焓变误差最大为±5%。

2 帕尔贴原理与分析

帕尔贴效应是指电荷载体在不同的材料中处于不同的能级，当它从高能级向低能级运动时，便释放出多余的能量；相反，从低能级向高能级运动时，从外界吸收能量。

帕尔贴的模型结构图如图1所示，由N、P两种类型的半导体温差电材料经电导率较高的导流片串联构成。当电流流过回路时，将在接头A处发生吸热，而在接头B处放热，因而在A、B两端建立温差ΔT=Th-Tc。

帕尔贴冷端吸收的热量Qc以及热端放出的热量Qh分别通过式(4)和式(5)计算。

(4)

(5)

式中；Rp为N、P电偶臂的电阻；α为N、P电偶臂的温差电动势总和，与制冷器的电偶臂对数有关；I为通过回路的电流；K为热导率；Th和Tc分别为帕尔贴热端和冷端的温度。

帕尔贴元件消耗的总功率P由式(6)给出：

P=Qh-Qc=α(Th-Tc)I+I2Rp

(6)

帕尔贴最大温差Tm和最大产冷量Qcm是影响其性能的关键参数。从冷端热平衡方程式(4)推导得到冷热端温差：

(7)

制冷器无外加热负载即Qc=0，令d(ΔT)/dI=0，从而求得ΔT为最大值时的最佳电流Im和冷热端最大温差ΔTm：

Im=αTc/Rp

(8)

(9)

在制冷器冷端热平衡方程式(5)中，令d(Qc)/dI=0，从而求得Qc为最大值Qcm时的最佳电流Ic：

Ic=αTc/Rp=Im

(10)

(11)

然而实际使用时，由于内阻Rp的变化、热端温度Th无法保持恒定、负载Qc≠0等问题，ΔTm和Qcm很难准确计算，因此控制模型难以建立。

3 温控腔体结构设计

针对上一节中提出的帕尔贴运用难点，同时为满足悬臂梁气敏材料表征实验对温度环境和腔体大小的需求，本文设计了基于双层帕尔贴结构的小型化腔体，如图2所示。

温控腔体主要包括5个主要部分：

(1)2套相互独立的温控系统分别测量与控制腔体顶部与底部金属壁温度，从而保证两侧都能准确达到目标温度。

(2)上下两侧的帕尔贴元件均采用双层结构，外侧帕尔贴为内侧帕尔贴散热，并与水冷散热结构进行热交换，内侧帕尔贴由电路控制其工作电流从而控制温度。内侧元件型号选用TEC1-3505，外侧元件选用TEC1-3506，最大温差均为75 ℃，因此双层结构可以使温度范围扩大到-40～180 ℃。

(3)散热系统由恒温槽提供循环液进行热交换。

(4)顶部和底部的腔体壁分别连通外部导管，将实验气体导入实验腔体内。

(5)利用帕尔贴对上下腔体壁进行温度控制，再通过腔体壁与腔体内气体之间的热传递作用实现实验环境温度的间接控制。腔体为圆柱体，高度为2 cm，底面半径为3 cm，整体体积较小，有效避免了温度梯度的影响。

4 硬件电路设计

硬件电路主要组成见图3，主要分为3部分：温度检测电路、驱动电路、信号处理系统。

4.1 测温电路

利用铂电阻阻值随温度线性变化的特点，设计高信噪比、高分辨率的温度检测电路。同时加入自校准电路，保证电路工作不受器件温漂、零漂、时漂等影响。

信号调理电路由恒流源、放大、偏置、ADC、自校准电路组成，如图4所示。

电路中使用运算放大器搭建恒流源、二级偏置放大和低通滤波器电路，使用仪表放大器设计一级放大电路。整体电路的传递函数表达为

Vout=G1G2G3IdRpt+G2G3Vbias

(12)

式中：G1为一级放大的增益；G2为二级放大的增益；G3为低通滤波器对带宽内信号的增益；Id为由运放构成的恒流源电路输出电流；Rpt代表Pt100；Vbias为二级放大电路中电压偏置。

由于电路元器件的误差及漂移，实际电路传递函数表达式往往与式(12)不同。主要误差来源于以下几个方面：电阻阻值的误差；运算放大器输入失调电压、输入失调电流、输入偏置电流；仪表放大器输出失调电压、放大倍数漂移、参考电压误差；偏置电压误差。

电路实际工作温度约为10～35 ℃，分别分析下列4种情况下输入阻值为80.306～175.856 Ω时电路输出曲线：25 ℃下无误差输出函数曲线；25 ℃下有误差输出函数曲线；10 ℃下有误差输出函数曲线；35 ℃下有误差输出函数曲线。图5为电路输出曲线对比图。由于电路具有较好线性度，因此传递函数可以简化为y=kx+b，不同情况下输出函数的不同主要体现在参数k和b的不同，表1列出上述4种不同情况下输出函数线性表达式对比。

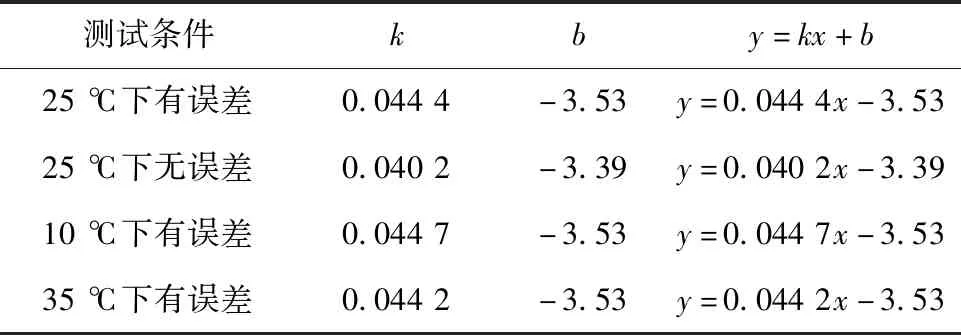
表1 电路输出函数对比表

为了避免电路中器件误差以及温漂、时漂导致的测温不准确，需要进行测试并拟合输入与输出的关系从而找到实际输出函数。但是这种方法在大批量生产时测试成本较高，并且温漂与时漂的影响依然无法避免。

假设实际电路线性输出函数为y=kex+be，ke和be可以通过2组输入输出数据计算得到。待测电阻串联2个高精度低温漂电阻RJ711，并通过模拟开关选择输入电路的电阻。每次启动程序时，分别将100 Ω和150 Ω的电阻接入电路中测出输出，并通过解方程组的方法得到ke和be，从而得到实际电路输出函数。输入电阻Rin1=100 Ω对应输出为Vour1，输入电阻Rin2=150 Ω对应输出为Vout2，得到方程组：

(13)

解方程组可得：

(14)

这种方法通过引入高精度低温漂电阻，将电路中所有误差项全部转化为2个精密电阻的误差，电路的制作只需要保证RJ711的准确性即可得到准确的电路输出函数，实现了低成本高精度的自校准测温电路。

4.2 驱动电路

帕尔贴的控制通过MCU输出不同占空比的PWM实现。本文选用的2种帕尔贴的最大温差电流是5 A和6 A，最大温差电压都是4.2 V。然而实际使用时，由于散热不及时、器件内阻增大等影响，最大温差电流和最大温差电压往往是规格中的70%～80%，所以驱动电路驱动一块帕尔贴需要4.2 A/3 V。温控腔体加热面为上下两面，每一面由一个驱动电路驱动6块帕尔贴工作，驱动电路需要提供4.2 A/18 V的电流/电压输出。本文根据设计需求，选用高效、高电流功率驱动器DRV595，其最大可提供±4 A输出电流，26 V输出电压，电路如图6所示。

4.3 控制方法

针对帕尔贴内阻易变、冷热两面温差不定、外界水循环散热效果有限、双层帕尔贴结构复杂等问题，本文选择模糊自适应PID算法，实现全温控范围内快速精确的控温效果。

比例积分微分(PID)控制是工业和其他领域中受欢迎的控制方法，结构简单、鲁棒性强等特点使其能满足工业控制中的要求，更好地适应控制过程中遇到的各种变化以及干扰。

位置式数字PID算法公式：

(15)

式中：e(k)为第k次的误差；ec(k)为第k次的误差变化率；Kp、Ki、Kd分别为比例系数、积分系数、微分系数。

模糊逻辑控制(fuzzy logic control)是基于模糊数学的控制方法，它通过模仿人类在手动控制时的思维方式，来识别和决定模糊现象，然后再根据输出的模糊量进行去模糊化操作，最终输出精确的控制量，从而实现对被控对象进行控制。

模糊自适应PID控制结合了Fuzzy和PID两者的优点，利用Fuzzy系统对PID控制系统的参数进行实时自调整，从而优化PID控制器的控制效果[8]，其结构如图7所示。

图中，r(t)为控制目标函数，y(t)为系统输出函数，e(t)为误差函数，ec(t)为误差变化率函数，输出为PID参数调整量ΔKp、ΔKi、ΔKd。模糊系统推理为Mamdani型，隶属函数使用三角型和高斯型2种，模糊规则见表2、表3、表4。

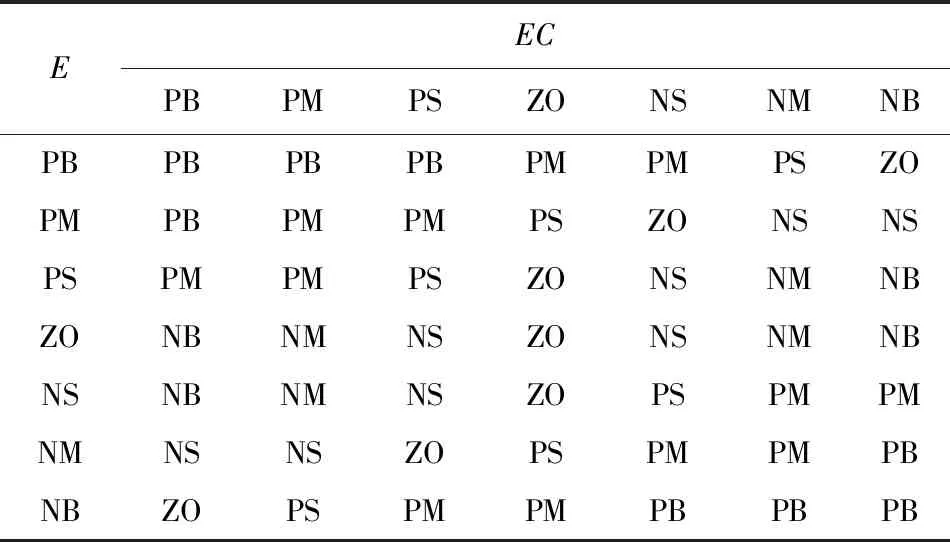
表2 ΔKp规则表

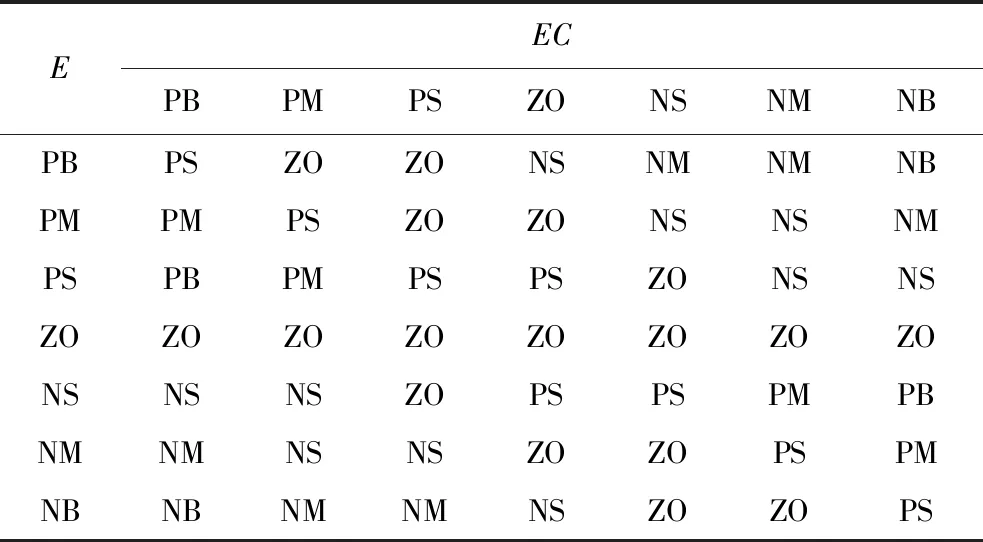
表3 ΔKi规则表

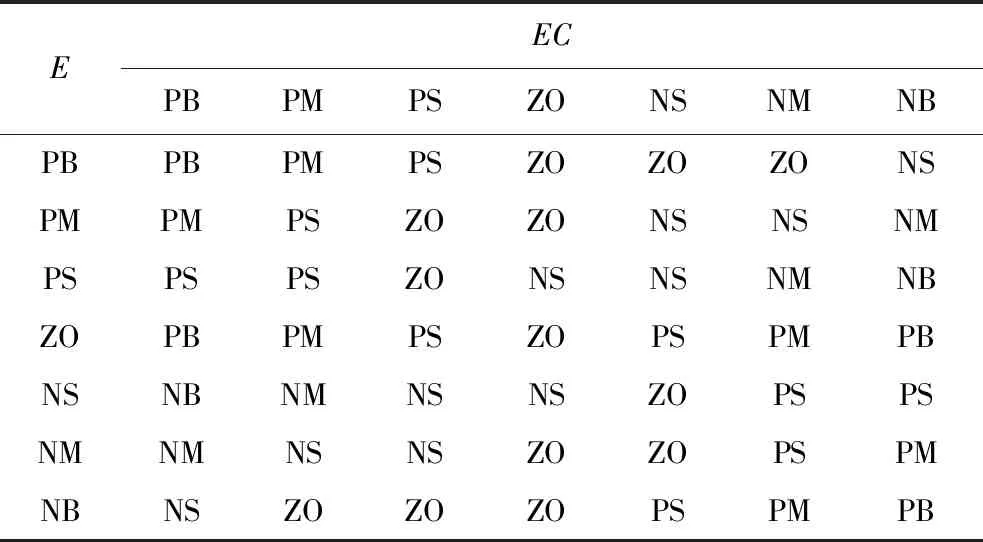
表4 ΔKd规则表

5 实验结果与讨论

5.1 测试设备

测试设备实物图如图8所示，温控电路板如图9所示。电路板通过驱动检测线与腔体上下极板内的Pt100和帕尔贴相连；帕尔贴通过水冷循环系统实现散热；腔体通过升降上极板实现打开或关闭。

5.2 温控测试结果

5.2.1 Fuzzy-PID与PID对比测试

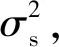
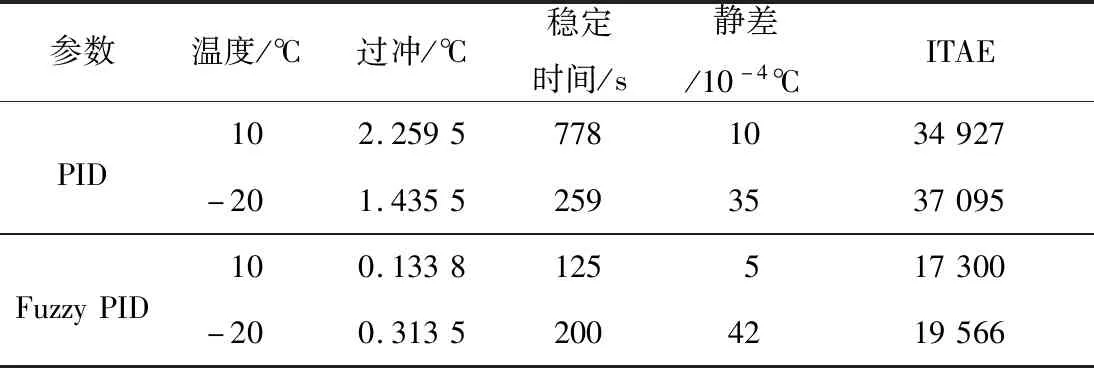
表5 PID与Fuzzy PID对比表

(16)

从实验结果中可以看出，PID控制在10、-20 ℃ 2个温度点的控制中，过冲温度值均大于1 ℃，而Fuzzy-PID的温控过冲温度值均小于0.5 ℃；相比PID，Fuzzy-PID在-20 ℃的控制稳定时间优化23%，在10 ℃的控制稳定时间优化84%；2种控制方法的温控静差相差不多，均有较好控制效果；对于控制性能评估函数ITAE，Fuzzy-PID也远远优于PID，优化效果接近50%。总体而言，Fuzzy-PID相比于传统PID，具有更出色的控制效果。

5.2.2 温控范围及温控精度测试

图11为-40、60、180 ℃温度点处的温控稳定性，温度波动均在±0.05 ℃以内。

图12为全温度范围内的温控曲线图。本文选取-40、-30、-20、10、30、60、150、180 ℃这8个温度点进行温控测试。从图12可以看出，该温控系统在这8个温度点均有较好的温控效果。因此，该帕尔贴温控系统可以在-40～180 ℃温度范围内实现温度控制。

6 结束语

本文设计了将半导体制冷技术应用于悬臂梁气敏材料特性表征的温控系统。通过高精度自校准电路测得准确温度，并由MCU计算控制量，再利用DRV595电路驱动半导体元件帕尔贴实现温控。实验表明：该温控系统温控范围为-40～180 ℃，稳定性为±0.05 ℃，最大升温速度为40 ℃/min，最大降温速度为-20 ℃/min。相较于传统制冷温控方式，该系统可使气敏材料性能表征设备体积显著缩小、精度进一步提高，并且更易于系统集成。