非贯通锯齿状结构面剪切破裂演化机制试验研究
吉 锋,闫兴田,张 波
(1. 成都理工大学 地质灾害防治与地质环境保护国家重点实验室,四川 成都 610059;2. 中国电建华东勘测设计院(福建)有限公司,福建 福州 350000)
0 引 言
岩体包括了岩石和结构面两个部分,岩体的变形及破坏特征在很大程度上由结构面控制。大量工程岩体(如边坡、坝基等)的破坏和失稳,通常是由于外界条件的改变,裂纹沿着力学性质较薄弱的地方发展,最终使结构面贯通而引起的[1]。
在工程地质学中,将岩体的结构面按照几何形态划分可以分成平直状、波浪状、锯齿状和台阶状4类[2]。在硬性岩体的自然边坡中,锯齿状结构面十分常见,图1(a)为乐山马边滑坡左边界锯齿状结构面,经简化得物理模型示意如图1(b)。

图1 力学模型示意Fig. 1 Schematic diagram of mechanical model
目前,已有许多学者对节理岩体的破坏机制及理论、贯通扩展影响因素、岩桥弱化、贯通准则等方面进行了详实的研究。
周瑞光等[3]研究了锯齿状结构面的剪切破坏机制,认为锯齿状结构面在整个剪切变形过程中可分为剪变形、剪破坏和剪碎带改造3个阶段;范景伟等[4]通过石膏模型试验,考虑了裂纹间的相互作用,探究了节理长度、贯通率以及充填情况等特征对强度的影响规律;徐靖南[5]基于模型试验,建立了共线节理岩体在压剪状态下的破坏模式;李海波等[6]通过剪切试验研究了不同剪切速率下具有不同岩石节理倾角度的岩石节理强度特征;刘远明等[7]对在直剪条件下非贯通节理岩体试验研究进展进行了较为详细的论述,对其变形破坏机理和剪切强度准则进行了归纳;王茜等[8]运用计算机技术,通过数值模拟分析了不同倾角结构面岩体在三轴压缩条件下的应力应变的关系,并从微观角度分析了结构面的变形性质。
在岩体强度特征方面,早在1969年,E.Z. LAJTAI[9~10]就提出了Lajtai岩桥破坏理论。近年来,李肖音等[11]引入了分形维数,得到了适用于粗糙节理岩体的库仑强度修正公式;沈明荣等[12]对岩体中锯齿状结构面的蠕变特性进行了研究;刘远明等[13]通过修正 Lajtai 理论,建立了非贯通节理岩体的贯通破坏强度准则;周莲君等[14]对结构面剪应力的分布特征进行了研究,得到剪应力及法向应力的分布规律;郭牡丹等[15]引入贯通系数变量描述贯通强度与峰值强度的比值变化,定量分析贯通强度与结构面摩擦系数、围压、连通率和结构面倾角之间的函数关系;乐慧琳等[16]对不同尺寸的具有锯齿状结构面的试样进行直剪试验,得到不同尺寸结构面的抗剪强度;吴仕鹏等[17]运用FLAC3D软件对结构面力学性质的影响因素进行了分析,并探究了剪切强度与锯齿状倾角的变化关系;黄达等[18]利用二维颗粒流程序,研究了倾角及法向应力对贯通型锯齿状岩体结构面的剪切变形及强度影响规律;夏才初等[19]考虑剪切过程中岩桥力学参数的弱化和节理面起伏角的影响,对Jennings准则进行了修正。
在实际工程中所遇到的岩体多为非贯通结构面岩体。随着研究的深入,非贯通节理岩体的强度特性越来越受到岩石力学界的重视,研究非贯通结构面对岩体的变形和破坏很有必要。
1 模型设计与制作
制取非贯通结构面试样较为复杂和困难,且所取同一试样难以保障一致性。为满足材料易取、便于成型、较短时间内强度足够等要求,以水泥砂浆为材料制作试样,具体配比为水泥∶石英砂∶水=1.0∶1.0∶0.4。非贯通锯齿状结构面剪切试验共设计3种不同锯齿状结构面倾角试样,结构面倾角α分别为18°、30°、42°,见图2,具体尺寸见表1。

图2 物理模型示意Fig. 2 Schematic diagram of physical model

表1 试样参数Table 1 Parameter of specimen
在试样浇注过程中,先浇注内部上下组合小块,放置约8 h,当具有一定强度后将其组合放置在模具的预定位置处,并浇注相同配比的水泥砂浆,使之成为一个整体,约24 h后拆开模具,将模型放入水中养护28 d。
2 结构面模型剪切试验
2.1 力学参数测试
共制作12个50 mm×50 mm×50 mm的完整试件,每两个分别施加σ为0.1、0.2、0.3、0.4、0.5、0.6 MPa的正应力,进行剪切试验,获得岩桥的抗剪强度参数;制作10个100 mm×100 mm×50 mm的完整试件,将其两两组合形成5个100 mm×100 mm×100 mm的试件,通过直剪试验获得平直结构面的抗剪强度参数;制作3个高100 mm、直径为50 mm的圆柱体试件,通过压缩试验获得岩桥的抗压强度。对试验数据进行处理后,获得岩桥和平直结构面的力学参数(表2)。

表2 强度参数取值Table 2 Value of strength parameter
2.2 非贯通结构面剪切试验
采用YDS-2型岩石力学多功能试验机对不同类型的非贯通锯齿状结构面试样进行剪切试验,法向应力σ分别为1.0、1.5、2.0、2.5、3.0 MPa,获得τ-us曲线(图3)。

图3 应力-应变曲线Fig. 3 Stress-strain curve
根据试验数据,获得不同非贯通锯齿状结构面倾角不同正应力下的抗剪强度(表3)。

表3 剪切试验结果Table 3 Shear test results
3 结构面模型破坏过程
3.1 破坏模式
根据岩桥及锯齿状结构面破坏模式,将含非贯通锯齿状结构面试样的破坏模式分为拉剪-剪胀破坏、拉剪-剪胀剪断破坏及剪切破坏3类。
3.1.1 拉剪-剪胀破坏
当正应力及结构面倾角较小时,试样在剪切力作用下,预设结构面张开,在结构面尖端产生应力集中,同时产生拉张裂纹;随剪应力增加,试样沿剪切面产生剪切裂纹,最终贯通;结构面上盘岩体沿预设锯齿状结构面发生爬坡运动,直至抗剪强度丧失,即发生破坏,如图4(a)。
3.1.2 拉剪-剪胀剪断破坏
当正应力及结构面倾角中等时,常发生拉剪-剪胀剪断破坏。该破坏模式与拉剪-剪胀破坏相似,但在结构面发生爬坡运动时,随爬坡高度增加,有效锯齿宽度减小,抗剪强度降低;当其所承受的剪应力超过其抗剪强度时,锯齿上部被剪断,岩体破坏,如图4(b)。
3.1.3 剪切破坏
当正应力及结构面倾角较大时,试样在剪切过程中,预设结构面张开程度不明显,且不产生明显的拉张裂纹,而是沿着剪切方向产生剪切裂纹;剪切裂纹随剪切力的增大逐渐发展、贯通,直至试样整体破坏,试样破坏面与剪切面近似平行,如图4(c)。

图4 破坏模式示意Fig. 4 Schematic diagram of failure mode
3.2 结构面角度及法向压应力对破坏模式的影响
根据试验结果,结构面倾角及法向压应力对非贯通锯齿状试样的破坏模式具有较大的影响。为避免重复,选取轴向应力为2 MPa时,不同类型结构面(α=18°、30°、42°)的破裂模式,以及B型试样在不同正应力(1.0、1.5、2.0、2.5、3.0 MPa)条件下的破坏模式来进行说明,根据破坏面特征分别做出素描图,如图5、图6。

图5 不同类型结构面试样剪切完成后素描Fig. 5 Sketch after specimen shear of different types ofstructural planes
由图5及图6可知,在其它条件相同的情况下,随结构面倾角或法向压应力的增加,在剪切破坏后,预先设置的结构面被剪断的部分越来越多,破坏模式渐由拉剪-剪胀破坏向拉剪-剪胀剪断、剪切破坏模式演变。
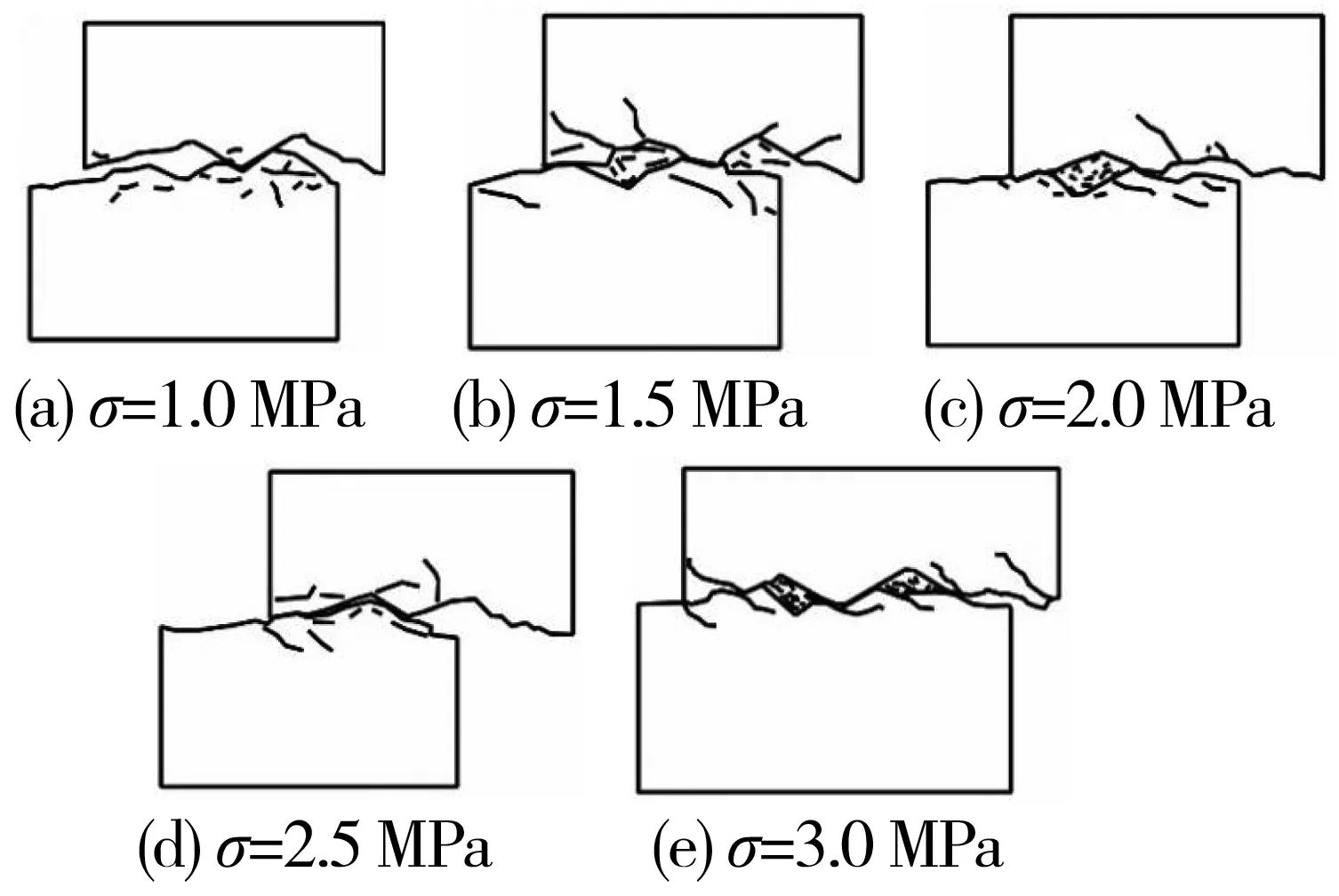
图6 不同轴压下剪切完成后素描Fig. 6 Sketch after shearing under different axial pressures
3.3 不同条件下试样剪切破坏模式
如3.1节所述,预设结构面倾角及法向压应力会影响其破坏模式。将不同实验条件下的剪切变形破坏模式进行汇总,其结果如表4。

表4 不同条件下试样剪切变形模式Table 4 Shear deformation modes of samples under different conditions
由表4可知,随着结构面倾角以及试样所受法向应力的增大,试样剪切变形破坏模式逐渐由拉剪-剪胀破坏向拉剪-剪胀剪断、剪切破坏模式演变。
在岩桥贯通后,当结构面倾角较小时,所施加的剪切应力在平行于结构面的方向上分力较大,而在垂直于结构面的方向上较小,上盘岩体容易沿着结构面发生爬坡运动。随着预设的结构面倾角增大,平行于结构面的方向上的分力减小,而垂直于结构面的方向上的分力增大,发生爬坡运动所需的分力增大,施加的剪应力增大,当其所受剪应力大于其抗剪强度时,便发生剪切破坏。
而当法向应力较小时,在施加剪切应力的过程中,上盘岩体容易克服所受到的轴向压力,沿着结构面发生爬坡运动。随着上盘岩体所受到的法向应力增大,上盘岩体越来越难克服法向应力σ,且上、下盘岩体之间所受的摩擦力逐渐增大,在上盘岩体发生爬坡运动一段时间后,当其运动到强度较低的部位时,试样中预先设置锯齿状结构面被剪断。所以,当法向应力σ越来越大时,预设的结构面被剪断的部分就越多。由此可以推测,当法向应力σ足够大时,在结构面贯通后,上盘岩体几乎不会沿着预设的结构面发生爬坡运动,而是从锯齿底部直接剪断。
从表4中的变形破坏模式分布来看,这种破坏模式的改变随结构面倾角以及试样所受法向应力的变化呈现出近对称矩阵变化的规律。由此可推测,当结构面倾角达到某一临界值后,无论法向应力的值如何,试样均将发生直剪剪切破坏。
4 抗剪强度模型研究
4.1 强度模型建立条件
从20世纪50年代开始,国内外学者对非贯通节理岩体的抗剪强度做了大量工作。最具代表的是Jennings理论和Lajtai岩桥破坏理论。此外,很多学者在这两个理论的基础上进行了修正,使之具有更强的适应性。笔者基于摩尔-库伦准则的Jennings准则,引入结构面倾角,对试验数据进行拟合,从而提出一种新的抗剪强度公式。
影响非贯通结构面岩体的综合抗剪强度的因子众多,包括结构面连通率、强度、倾角、岩石强度、应力条件等,笔者仅考虑结构面倾角对其综合抗剪强度的影响。该强度模型建立的条件如下:除了非贯通结构面试样的结构面倾角不同外,其余条件均相同。
4.2 模型建立
根据剪切实验,获得相同正应力下含非贯通锯齿状结构面试样的抗剪强度随结构面倾角变化的关系(图7)。由图7可知,当结构面倾角为30°、正应力为2.5 MPa时,所对应的抗剪强度明显高于条件相近的抗剪强度值。因此,将此数据视为异常数据,将异常数据删除后得到修正后的抗剪强度(表5)。

图7 综合抗剪强度随结构面倾角的变化关系Fig. 7 Relationship of comprehensive shear strength changing withthe dip angle of structural plane

结构面下列正应力/MPa下峰值强度/MPa1.01.52.02.53.0A型结构面2.9383.1723.3823.9234.347B型结构面3.1063.4153.815—4.857C型结构面3.2653.5094.0314.8375.285
为验证模型的正确性,分别用A、B、C共3种类型结构面在1.0、1.5、2.5、3.0 MPa条件下相对应的抗剪强度对模型进行拟合,用2.0 MPa条件下的抗剪强度进行验证。
以不同类型结构面试样的剪切试验数据为基础,利用最小二乘法进行拟合(图8)。

图8 剪应力-法向应力关系Fig. 8 Relationship between shear stress and normal stress
通过拟合所得的线性表达式,利用摩尔-库伦准则的Jennings准则,即:
τ=σtanφ+c
(1)
式中:τ为抗剪强度,MPa;σ为轴向应力,MPa;c为黏聚力,MPa;φ为内摩擦角,(°)。
计算得到c和φ(表6)。由表6可知:随着结构面倾角的增大,内摩擦角(φ)及内聚力(c)均增大。由于结构面的存在会对试样的综合抗剪强度发生弱化效应,故其综合抗剪强度参数不会高于完整试样的强度参数。由此可推测,当结构面倾角达到某一值后,其综合抗剪强度不再改变。
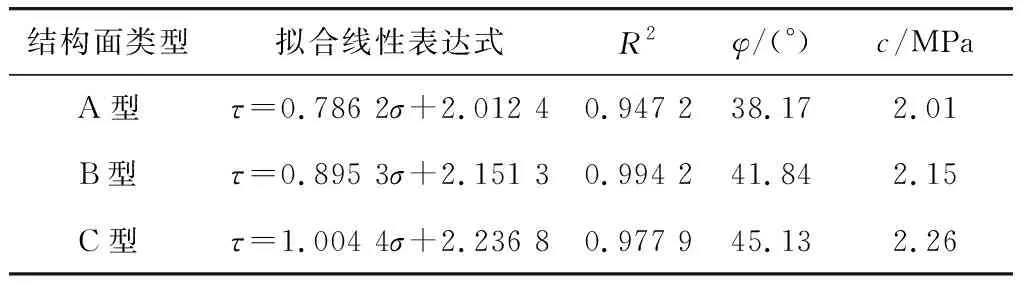
表6 不同试样抗剪强度指标计算Table 6 Calculation of shear strength index of different samples
通过分析,得出非贯通锯齿状结构面的抗剪强度与其所受的轴向压力大致呈线性关系,故非贯通锯齿状结构面的抗剪强度在形式上符合Jennings强度理论。故设非贯通锯齿状结构面综合抗剪强度满足式(2):
(2)
式中:cz、cj、cy分别为非贯通节理岩体、平直结构面、岩桥段的内聚力,MPa;φz、φj、φy分别为非贯通节理岩体、平直结构面、岩桥段的内摩擦角,(°);i为规则锯齿状结构面的倾角,(°);f(i)、g(i)为关于i的函数;k为连通率。
根据本次试验数据,对试样等效剪切强度参数与结构面倾角的关系进行拟合(表7),得到除结构面倾角不同外、其余条件相同情况下,非贯通结构面等效摩擦角和等效内聚力随结构面倾角变化的关系式。

表7 等效剪切强度参数与结构面倾角关系Table 7 Relationship between equivalent shear strength parametersand dip angle of structural plane
对于本次试验,φj=8.61°,cj=0.23 MPa,φy=47.24°,cy=2.28 MPa,k=0.6。将此数据带入式(2)中,结合表5中关系式,采用系数对比法可得:
φz=k(φj+0.483i+14.92)+(1-k)φy
(3)
cz=k(cj+0.017i+1.296)+(1-k)cy
(4)
即得非贯通锯齿状结构面的综合抗剪强度关于倾角的理论表达式:
(5)
4.3 模型验证
4.2节已得到关于结构面倾角的新综合抗剪强度经验公式〔式(5)〕。该式可反映出非贯通锯齿状结构面综合抗剪强度随结构面倾角变化的规律。为进一步验证式(5)的可信度,采用法向应力为2.0 MPa时的综合抗剪强度对该式进行验证。
用式(5)求得A、B、C 3组试样在正应力为2.0 MPa时的综合抗剪强度理论值,将其与试验值进行对比,求得误差值,结果见表8。

表8 综合抗剪强度理论值误差计算Table 8 Error calculation of theoretical value ofcomprehensive shear strength
由表8可知,试验值与理论值的误差均在10%以内,且式(5)能够反映出综合抗剪强度与锯齿状结构面倾角的变化规律,这说明利用笔者提供的公式能够对含非贯通锯齿状结构面岩体抗剪强度进行预测,且可信度较高,该综合抗剪强度模型合理。但由于此模型仅由人工浇筑试样进行实验推导完成,故仅适用于较为均质的块状岩体,对于层状或者含软化夹层的岩体,其可行性还有待做进一步验证。
5 结 论
采用水泥砂浆试样,模拟非贯通锯齿状结构面岩体在不同结构面倾角条件下的的剪切变形过程,得出以下结论:
1) 根据非贯通锯齿状结构面试样的破坏机制,可分为拉剪-剪胀、拉剪-剪胀剪断以及剪切破坏3种模式。随着预设的结构面倾角以及法向压应力的增大,破坏机制由拉剪-剪胀向拉剪-剪胀剪断以及直接剪切破坏转变。当结构面倾角达到某一临界值后,试样均将发生直接剪切破坏。
2) 随结构面倾角的增大,非贯通锯齿状结构面试样的等效黏聚力和等效内摩擦角均增大,综合抗剪强度增大。但当结构面的倾角增加到某一临界值后,结构面倾角将不会影响其综合抗剪强度,或对其综合抗剪强度影响非常小。
3) 基于摩尔-库伦准则的Jennings准则,引入连通率及结构面倾角对抗剪强度经验公式进行修正,得到非贯通锯齿状结构面综合抗剪强度关于倾角的理论表达式。结果表明,笔者修正后的公式能够反映出综合抗剪强度与锯齿状结构面倾角的变化规律,且可信度较高。

