一种桥梁实测小样本数据的区间优化方法——灰自助抽样与灰色系统理论相结合

郭慧鹏，陈旭勇，许峙峰，操 爽

武汉工程大学土木工程与建筑学院，湖北 武汉430074

在对桥梁进行非概率可靠性评估时，可靠性指标对区间参数变化非常敏感，区间估计准确度直接影响着桥梁可靠性评估的结果。农村公路桥梁受历史资料残缺、试验经费少等因素制约，区间参数数据主要来源于现场实测，因而获取的数据十分有限。如何对有限的样本数据进行处理优化，获取精确的参数区间对于非概率可靠性评估具有重要意义。

传统的概率参数估计方法需要大量的数据作为基础，并需要知道样本的总体分布形式。对小样本数据进行参数估计时需要事先假设样本的总体分布，而不合理的分布假设会直接影响参数估计的准确度。针对小样本数据少、贫信息的特点，可依据邓聚龙［1］提出的灰色系统理论以及刘思峰等［2］提出的灰色关联度进行研究。刘义等［3-4］基于小样本数据间的拓扑关系和距离关系提出了灰色距离测度这一概念，并给出了满足一定灰色置信度下的灰色置信区间的求解方法。吴云洁等［5］将重抽样方法与基于灰色系统理论的区间估计方法相结合，提出了小样本灰色置信区间的求解方法。杨文光等［6］在灰色距离测度中引入了样本误差均值和误差方差，提出了基于熵权法的参数估计方法。为了改善自助法抽样的局限性，Xia等［7］利用自助法和灰色系统理论的优点，提出了灰自助法用于小样本数据的参数估计，但对于区间估计的应用还不是很完善。曹欣等［8］在此基础上对原灰自助法抽样和数据拟合的方法进行了改进，避免了极小样本下的重复抽样，并对比了自助法和改进灰自助法的分布直方图，说明了改进灰自助法的优越性。陈柔伊等［9］将改进的灰自助法引入到了电力系统中进行可靠性原始参数预测。汪启跃等［10］将灰自助法应用到了乏信息随机振动信号的分析中，对功率谱密度进行了区间估计，并与自助法进行对比说明其区间估计的优势。柯肇捷等［11］提出了一种基于灰自助和未确知有理数的新方法，但对于区间估计还是需要假设样本的总体分布。目前，灰自助法已经航空航天、机械制造以及岩土工程等很多领域得到了应用［12-16］。

在以上研究的基础上，本文将灰自助抽样与基于灰色系统理论的区间估计方法相结合，应用到桥梁参数的区间估计中，并给出了具体的计算过程。该方法不依赖样本的总体分布，具有广泛的适用性。最后通过实例计算对比了3种区间估计方法的区间估计效果，验证了上述方法的合理性及有效性。

1 相关理论及定义

1.1 灰自助法

自助法抽样是在原始样本范围内重复抽样，扩展样本数。但抽样局限于原始样本范围内，当样本极小时，不可避免地会出现重复抽样，造成的误差会在原始样本数据误差的基础上继续扩大，使结果极大地偏离真实分布。

灰自助法将灰色GM（1，1）预测模型与自助法结合起来，改善了自助法抽样局限于原始样本范围内的缺陷，避免了重复抽样。本文采用经验分布进行抽样，其原理如下：

假设桥梁某参数现场实测所得样本数据列向量为

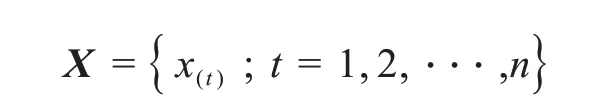
根据自助法抽样，将数据由小到大进行排序

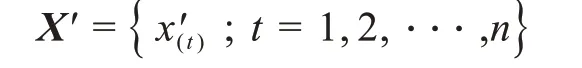
经验分布的函数值为

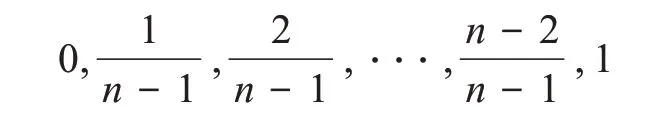
对经验分布进行抽样的过程为

1）在（0，1）区间产生随机数r；

2）令β=（n-1）r，i=int（β）+1；

重复抽样n次可得第一个自助样本，重复多次，即可得到多个自助样本。对每个自助样本分别进行升序、降序排列，分别通过灰色GM（1，1）预测模型预测下一个值，相当于对每个自助样本区间边界进行了扩展，改善了自助法在原始样本范围内抽样的局限性。灰色GM（1，1）预测模型原理如下：

对每个自助样本排序后累加生成新的数据序列，按均值生成法构造背景值

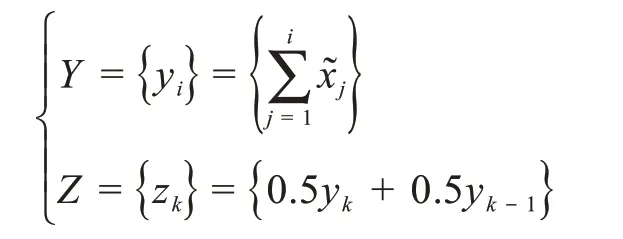
其中，Y为x1,x2,···,xi相加的和，Z为背景值函数。

建立GM（1，1）模型的白化方程为

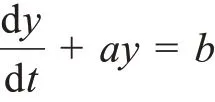
估计发展系数a，灰色作用量b

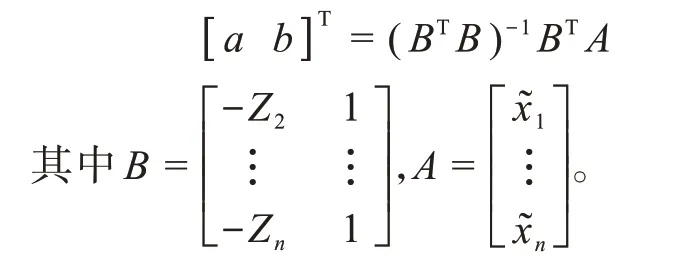
求解得到相应函数为

通过累减还原得到该样本的预测值。

1.2 灰色系统理论

灰色系统理论是将每个样本与整个样本空间的距离关系定义为灰色距离测度，在给定的灰色置信度下求解灰色置信区间。

1）计算样本中某一数据相对于样本中其他数据的灰色距离

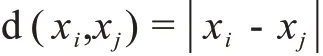
2）计算样本中所有样本点的平均灰色距离

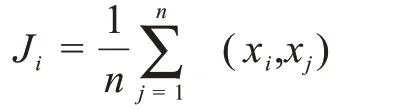
3）计算每个样本点的灰色权重

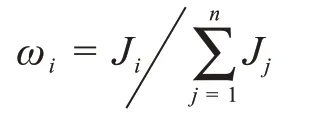
4）整个样本的灰色估计值

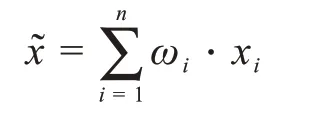
5）在给定的灰色置信度α下，灰色置信区间为

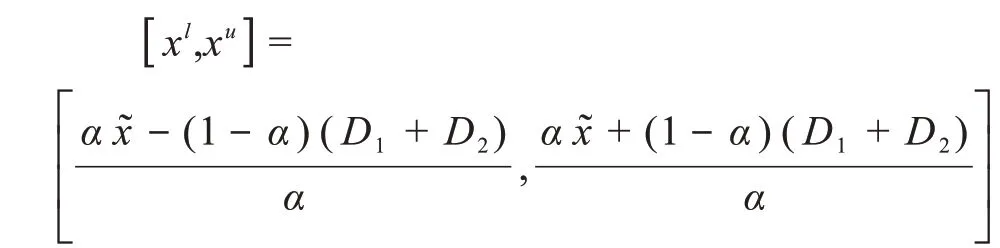
6）求解每个样本的灰色置信区间，通过取交集的方式获取更加精确的灰色置信区间。

2 实例验证与方法比较

自助法抽样由于在原始样本范围内进行抽样，不可避免地会造成区间估计结果更窄，估计结果会与实际出现较大偏差。本文方法是在文献［5］的基础上改进了抽样方法，利用灰自助抽样取代自助法抽样，改善自助法抽样的局限性。为更好地验证本文所提方法有效性，下面通过实例进行比较分析。

以实测桥梁混凝土强度的数据作为小样本数据，样本X=｛35.1，34.1，33.7，33.9，35.6，35.0，33.8，35.3，34.3，34.9｝，共10个样本数据。

1）基于灰色系统理论的区间估计方法：

取灰色置信度为0.6，根据灰色系统理论方法算得灰色估计值为34.589，灰色置信区间为［33.956，35.222］，区间宽度为1.267。

2）自助法抽样与基于灰色系统理论的区间估计方法相结合：

取灰色置信度为0.6，计算得到原始样本以及4个抽样样本的置信区间，通过取交集的方式得到最终的置信区间如表1。

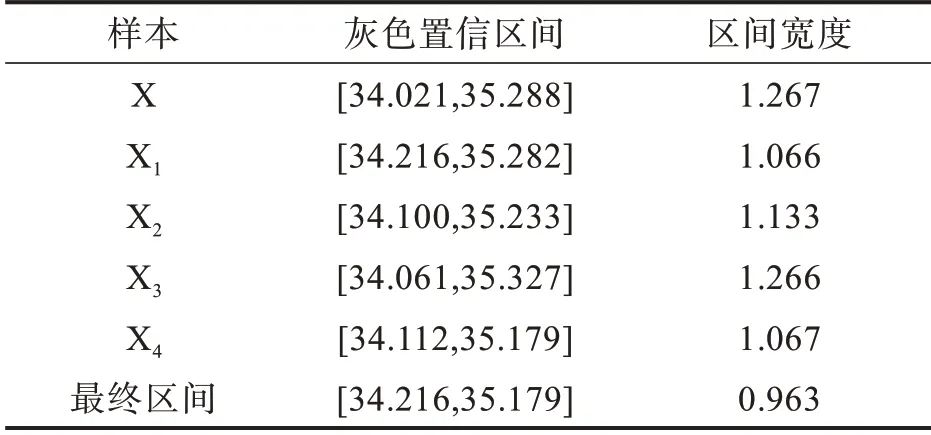
表1 各样本的灰色置信区间Τab.1 Gray confidence intervals of each sample

3）本文方法：

本文将灰自助抽样与基于灰色系统理论的区间估计方法相结合来对小样本数据进行区间估计，该方法无需知道样本的总体分布形式。取置信度为0.6时，计算得到原始样本以及4个抽样样本的置信区间，通过取交集的方式得到最终的置信区间如表2。

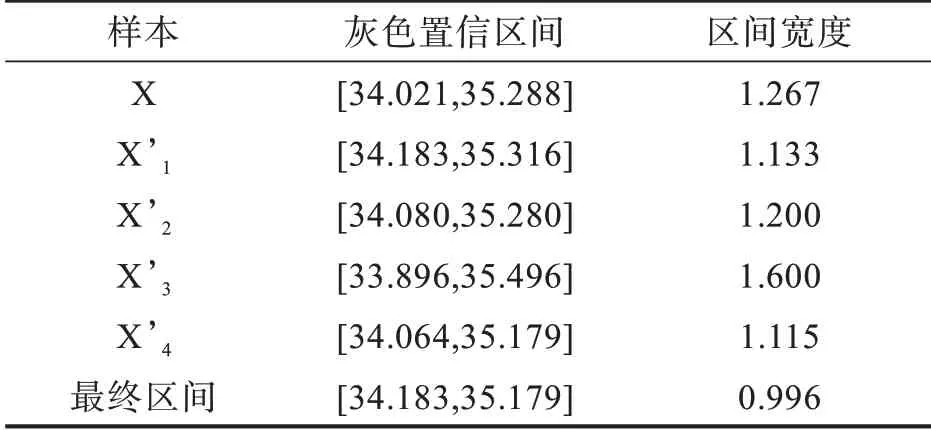
表2 各样本的灰色置信区间Τab.2 Gray confidence intervals of each sample

将以上3种方法获得的置信区间进行对比可以发现，当采用自助法对原始样本进行扩充获得多组相似样本后，各相似样本的灰色置信区间相互交错，通过取交集可以排除随机误差对结果的影响，进而获得更加精确的灰色置信区间。

图1将3种方法在不同灰色置信度下的置信区间进行了对比。从图1中可以看出，任一相同灰色置信度下，方法2和方法3计算得到的区间宽度更窄，这是因为方法2及方法3采用自动法抽样对原始样本数据信息对样本数据进行了扩充，获取了大量有效信息，弥补了统计理论在小样本数据估计中的不足，估计的精度更高。而方法2得到的区间宽度比本文方法更窄，但由于自助法抽样局限于原始样本范围内，所以并不能说明其结果更加可靠。

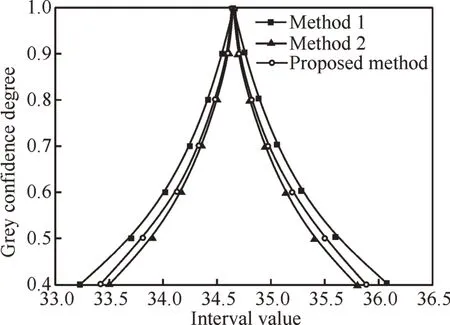
图1 3种区间估计方法的置信区间比较Fig.1 Comparison of confidence intervals of three interval estimation methods

为了说明本文方法得到的结果相比于方法2更加符合实际。本文将算例中实测的混凝土强度样本数据作为原始样本，灰自助法及自助法仿真样本数均为1 000，对比其通过灰自助抽样以及自助法抽样后的样本分布。

大量实测及统计数据表明，混凝土强度服从正态分布，故原始密度函数服从正态分布。从图2中可以看出灰自助抽样的分布明显好于自助法抽样分布。在小样本的情况下，灰自助法抽样得到的样本分布更加接近样本的真实分布，其分布更加平滑。而自助法抽样局限在原始样本范围内，所以其样本分布与样本真实分布相差较大，而且连续性也不强。故在本文所采用的抽样方法所获得的样本更加符合实际，最终计算得到的区间估计结果也更加可靠。

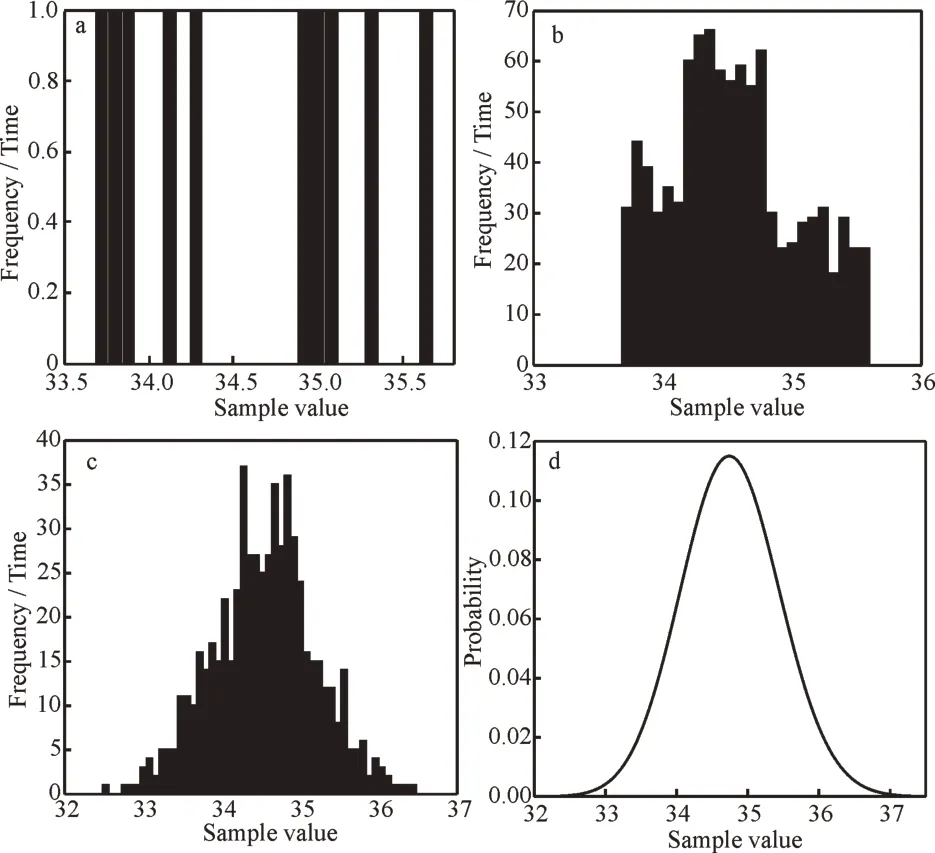
图2 样本分布：（a）原始样本，（b）自助法样本，（c）改进灰自助法样本，（d）原始样本真实分布密度Fig.2 Sample distribution：（a）original sample，（b）bootstrap sample，（c）improved grey bootstrap sample，（d）truedensity curve of original sample

3 结 论

对农村公路桥梁进行可靠性评估时，现场实测获得的桥梁参数数据有限。对于区间变量，其区间估计的准确性直接影响着可靠性指标的大小。针对小样本数据的区间估计，本文将灰自助抽样与基于灰色系统理论的区间估计方法相结合，将其应用到小样本数据的区间估计中。该方法具有以下特点：

1）灰自助法抽样通过灰色GM（1，1）预测模型对样本边界进行扩展，改善了自助法抽样局限于原始样本内的缺陷。

2）基于灰色系统理论的区间估计方法不依赖原始样本的分布形式，无需假设概率分布特征，能够有效解决小样本、贫信息问题中参数的区间估计。

3）算例的计算结果表明，本文所采用的方法在任意灰色置信度下区间估计的结果均好于基于灰色系统理论的区间估计方法。相较于方法2中的自助法抽样，本文的采用的灰自助法抽样是对自助法抽样进行了改进，改善了自助法抽样的局限性，通过其获取的样本更加接近样本的真实分布，故采用本文方法对农村公路桥梁参数进行区间估计时具有较高的可信度。