分割与扩展

◎蒋成法

有一块菜地，形状既不是长方形，也不是圆形，而是一个多边形，如下图ABCD：

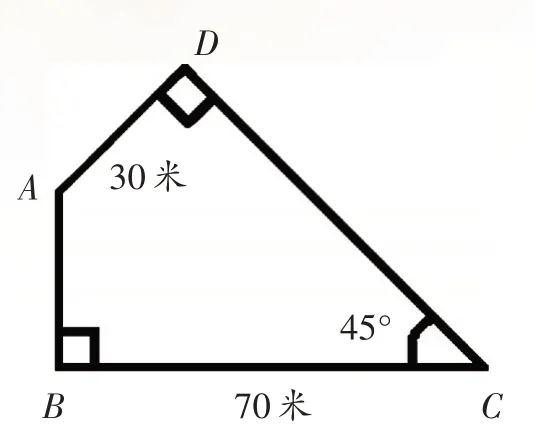
请你来帮忙算一算，这个菜地的面积有多大呢？

思路点睛：这是一个不规则图形，根据图上标出的数据，直接求出这块地的面积十分困难。

此时我们想到的是，能不能把这个不规则图形变成一个规则的图形呢？有两种方法，一种是分，也就是把图中的AC两点连接起来，分成两个三角形来计算。连一下试试：

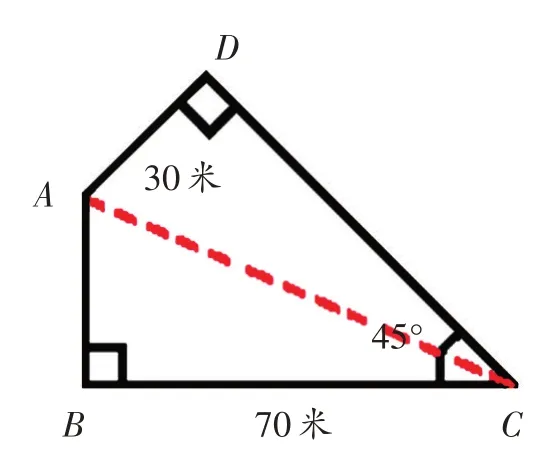
我们发现还是不行，因为分开后的两个三角形也缺少计算条件，只能知道其中的一条直角边的长度。

第二种方法，扩展。也就是从图形的外面来考虑，把这个图形扩展成一个规则的图形。我们可以利用辅助线将BA延长到E，将CD延长到E，这样就有了等腰直角三角形EBC（因为∠B=90°，∠C=45°）。

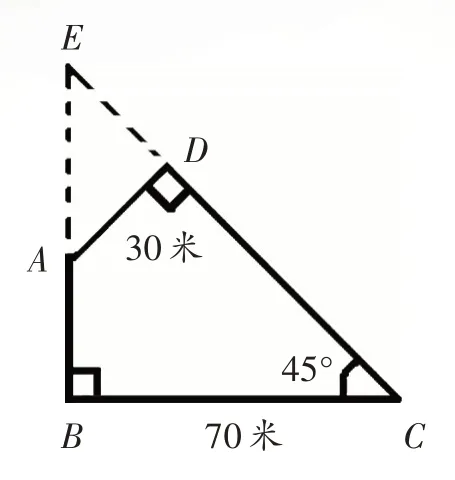
它的面积是70×70÷2=2450（平方米）。因为AD垂直CD，∠C=45°，∠E=45°，AD=30米，所以ED=30 米。那么三角形AED的面积就是30×30÷2=450（平方米）；于是可以求得四边形ABCD的面积是2450-450=2000（平方米）。

下面的这个图形是一个不规则的四边形，把它分成了三个部分，求中间阴影部分的面积。

思路点睛：先观察，然后想一想是用分割还是用扩展的方法。

很显然，扩展之后的图形数据还是不齐全，所以要试着对图形进行分割。

添加辅助线，把阴影部分分成两个三角形。

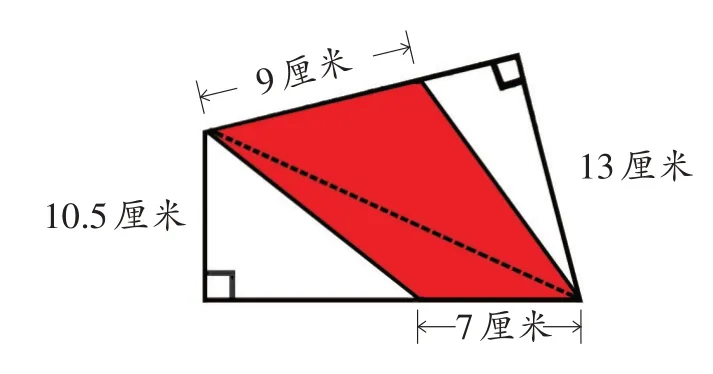
下面三角形的底是7 厘米，高是10.5 厘米，面积是7×10.5÷2=36.75（平方厘米）；上面三角形的底是9 厘米，高是13 厘米，面积是9×13÷2=58.5（平方厘米）。阴影部分面积是36.75+58.5=95.25（平方厘米）。