利用矢量网络分析仪单端口校准误差项提取二端口网络的S参数

孙 静，刘 晨，梁法国，霍 晔，栾 鹏，吴爱华

(中国电子科技集团公司 第十三研究所，河北 石家庄 050051)

1 引 言

在微波/毫米波测试过程中，通常需要获得测试系统中某个组成部分的二端口网络的S参数，如何使用最少的连接步骤，最优的校准方法是实现高准确度校准和测量的重要环节。例如负载牵引测量系统[1～4,19,20]和噪声参数测量系统[5，6]，其在线校准过程中，需要通过校准测量确定多个输入二端口网络和输出二端口网络的S参数。但是，这些测量系统结构复杂，尺寸很大，连线众多，接口包括3.5 mm、2.92 mm、2.4 mm波导和探针等不同类型，采用传统的两端口校准方法，无法实现测量系统中不同端口类型、超长或不同方向的二端口输入和输出网络的S参数测量。本文介绍了一种利用矢量网络分析仪两次单端口校准的误差项，提取二端口网络S参数的方法，该方法要求所求解的二端口网络具有互易性，即S12=S21。因此对于大多数的无源二端口网络，这种方法是适用的。

2 校准误差模型

目前矢量网络分析仪校准误差模型[7～16]有很多种，其中最经典的误差模型为12项误差模型(如图1所示)和8项误差模型(如图2所示)。其中12项误差模型将正向传输误差与反向传输误差分别加以对待。

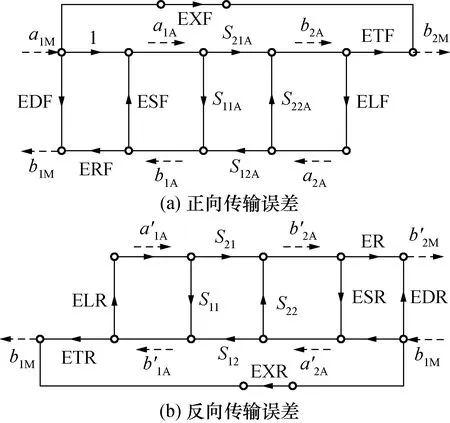
图1 12项误差模型Fig.1 12 terms error model

图2 8项误差模型Fig.2 8 terms error model

对于单端口校准，以正向传输误差而言，12项误差仅需要3项，即方向性误差(EDF)、源匹配误差(ESF)和反射跟踪误差(ERF)。这3项误差与8项误差模型的对应关系如式(1)～式(3)所示。

EDF=E00

(1)

ESF=E11

(2)

ERF=E01E10

(3)

8项误差模型不区分正向误差与反向误差，因此在求解8项误差模型的过程中，需要进行额外的开关项(switch term)校准，以消除由于矢量网络分析仪正向与反向非对称而引入的误差。在如图2所示的8项误差模型中，可以将误差网络看作是分别级联在被测件左、右端口的两个二端口网络，如果使用T参数来表示，可以写成如式(4)所示的形式：

TM=TEX·TDUT·TEY

(4)

式中：TM为矢量网络分析仪直接测量得到的未校准数据；TEX为误差网络X的T参数；TDUT为被测件的T参数；TEY为误差网络Y的T参数。

3 二端口网络S参数的确定

如图3所示，连接被测量的二端口网络前后，分别在矢量网络分析仪的参考平面Ⅰ和参考平面Ⅱ上做两次单端口校准，每次校准完成后，都可以使用SCPI命令提取矢量网络分析仪内部存储的误差项。以KEYSIGHT公司的PNA系列矢量网络分析仪为例，其提取内部存储的误差项的SCPI指令为，“SENSe:CORRection:CSET:DATA”，利用该指令可以得到单端口校准后的方向性误差(EDF)、源匹配误差(ESF)和反射跟踪误差(ERF)。

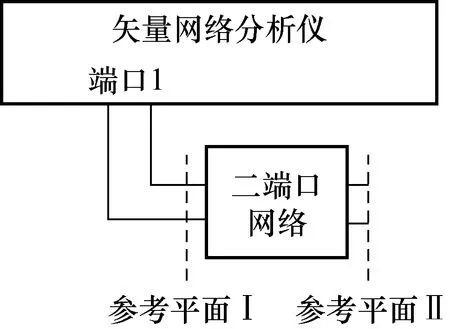
图3 两次单端口校准的参考平面示意图Fig.3 Diagram of difference planes for two one-port calibrations

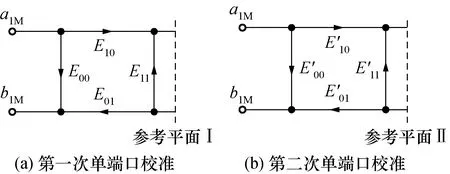
图4 第一次单口校准和第二次单口校准的误差模型Fig.4 Error models of the first one-port calibration and the second one-port calibration

根据S参数的级联关系，将第二次单端口误差项等效成第一次校准误差项与被测件级联，如图5所示，即：

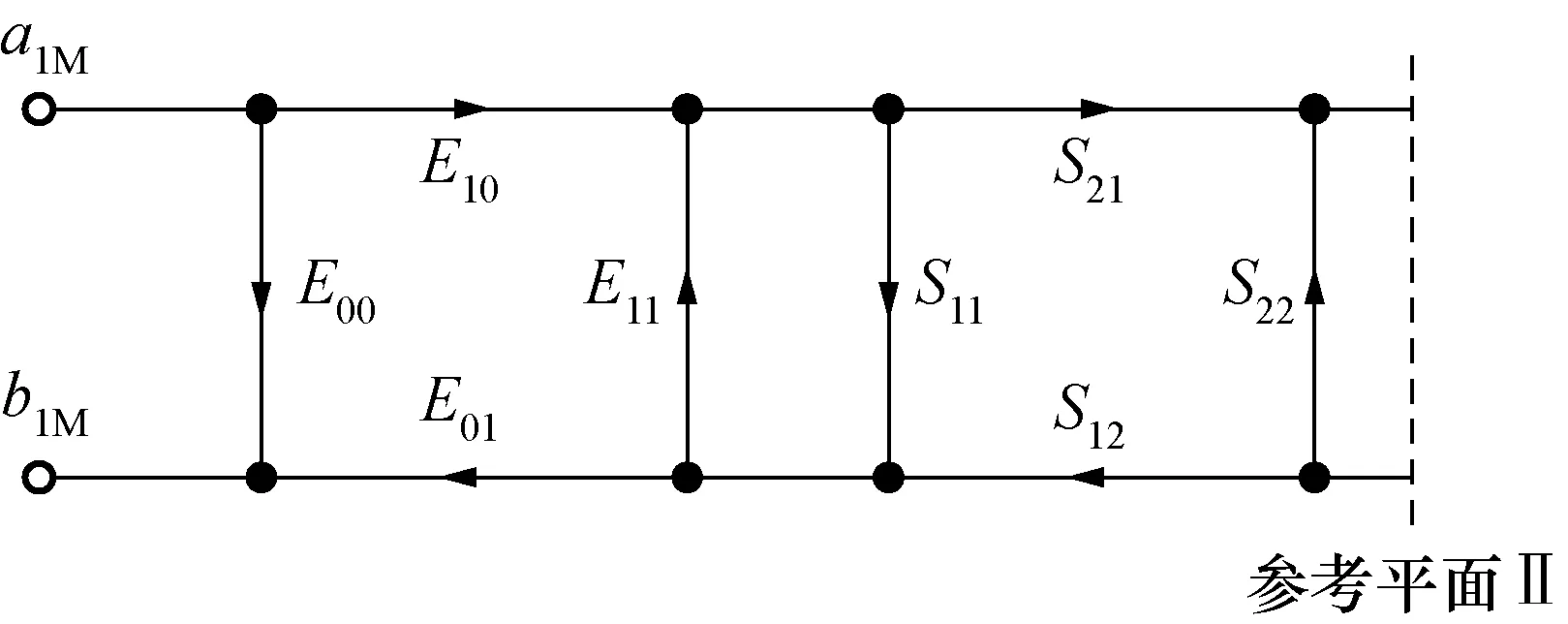
图5 第二次单端口校准的等效误差模型Fig.5 Equivalent error model of the second one-port calibration

(5)

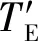
根据T参数与S参数的关系，可得式(6)：

(6)

将式(1)～式(3)代入式(6)，得到式(7)：

(7)

式中：EDF、ESF、ERF为第一次单端口校准的12项误差项；EDF′、ESF′、ERF′为第二次单端口校准的12项误差项。以上6个参数均可以在矢量网络分析仪校准后利用SCPI指令得到。

根据式(7)中第一个方程，不难求得：

(8)

为了计算方便，设x=1-ESF·S11，根据式(8)求解S11后，即可得到x。然后分别根据式(7)中第2个方程和第3个方程，可得：

(9)

S22=ESF′-ESF·x

(10)

由于所求二端口网络具有互易性，因此：

(11)

4 实验验证

为了对以上算法进行验证，选择10 dB衰减器作为被测件，使用矢量网络分析仪进行全二端口校准，测量其S参数作为参考值。

使用机械校准件在矢量网络分析仪一端口上进行单端口校准，然后分别利用SCPI命令“SENS:CORR:CSET:DATA? EDIR,1,1”提取误差项EDF，“SENS:CORR:CSET:DATA?ESRM,1,1”提取误差项ESF，“SENS:CORR:CSET:DATA?ERFT,1,1”提取误差项ERF。在一端口上连接被测件(10 dB衰减器)，并在衰减器另一端使用相同的机械校准件进行单端口校准，利用上述相同的3条SCPI命令提取误差项EDF′、ESF′、和ERF′。

图6和图7分别展示了利用本文所述方法对10 dB衰减器提取的S11和S21幅度与参考值(矢量网络分析仪直接测量二端口器件得到的值)的对比情况。从图中可以看出，本文所述的方法提取的二端口器件S参数是可行的。提取值与参考值存在的误差在可接受的范围内，误差主要来源是系统测量的重复性以及校准不完善。

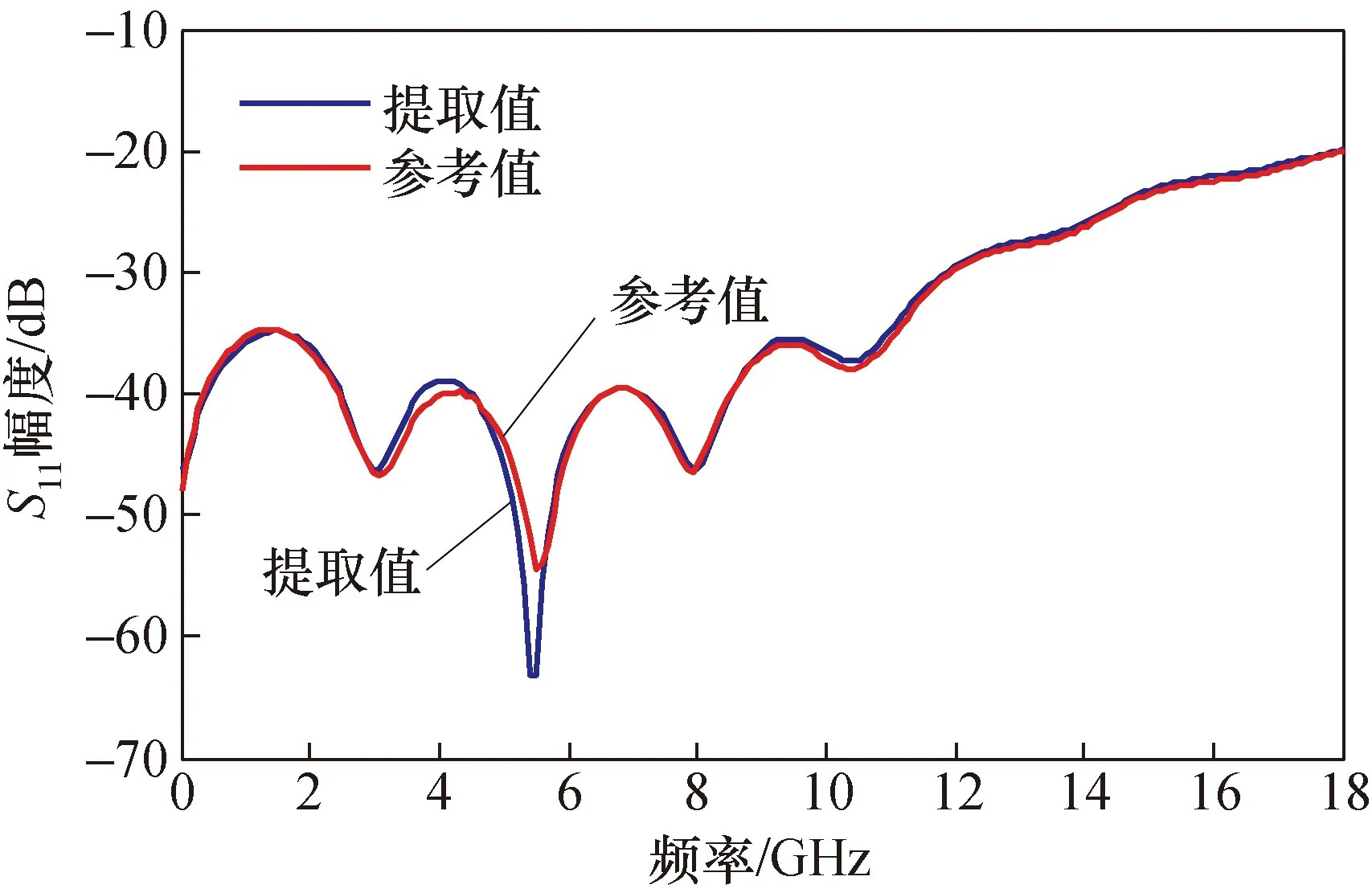
图6 S11幅度的提取值与参考值比较Fig.6 Comparison of extraction values and reference values for S11 amplitude

图7 S21幅度的提取值与参考值比较Fig.7 Comparison of extraction values and reference values for S21amplitude

5 应用实例

微波探针[17，18]是测量芯片的重要媒介，通过与芯片的物理接触，建立起测量系统与芯片之间的信号连接通道。微波探针是典型的非对称两端口微波网络，一端为同轴端，另一端为探针尖，微波探针结构如图8所示。微波探针是无源器件，属于互易网络(S12=S21)。通过上述的测量方法和测量理论，可以建立微波探针测量模型，计算得到其S参数。

图8 微波探针实物图Fig.8 Microwave probe physical diagram

由于微波探针的测量模型中会包含较多的复数参量(S参数)，采用GUM方法根据测量模型评定不确定度，其S参数偏导数不易求解，因此本文用MCM方法评定微波探针S参数不确定度，根据测量模型，依托MATLAB开发平台，将输入量通过测量模型进行传递，获得微波探针S参数的不确定度，解决了微波探针测量不确定度评定问题。图9～图11是评定的微波探针S参数的测量不确定度曲线图。如图所示，中心的绿线表示测量值，上边蓝线表示测量值加上测量不确定度的量值，下边红线表示标准值减去测量不确定度的量值。

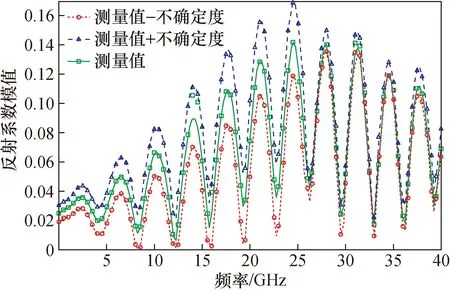
图9 微波探针同轴端反射系数模值Fig.9 Amplitude of reflection coefficient at coaxial port of the microwave probe

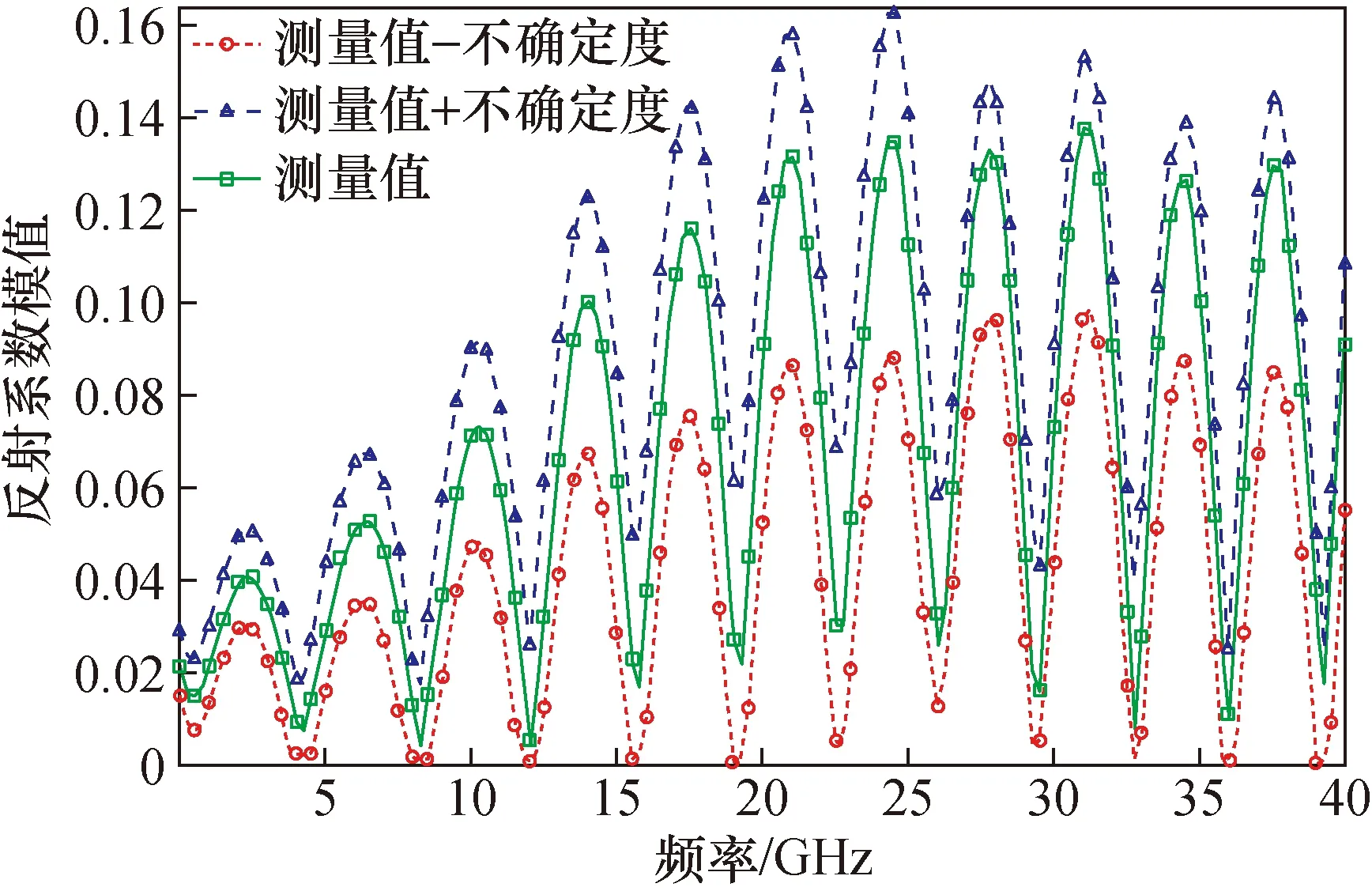
图10 微波探针尖端反射系数模值Fig.10 Amplitude of reflection coefficient at tip of the microwave probe

图11 微波探针传输幅度Fig.11 Transmission amplitude of the microwave probe

6 结 论

本文介绍了一种利用两次单端口校准的误差项，提取互易二端口网络S参数的方法，并通过实验验证了方法的正确性，最后介绍了微波探针采用该方法提取S参数和评估测量不确定度的实例。该方法可应用于负载牵引测量系统和噪声参数测量系统的在线校准求解级联无源网络S参数的过程中，另外，对于二端口矢量网络分析仪某一个端口出现故障时，该方法也可作为测量无源二端口网络S参数的一种方法。