单相PWM整流器H∞改进型直接功率控制

刘浩然，马磊，彭林，宋文胜，韩一丹

(西南交通大学 电气工程学院，成都 610031)

0 引 言

单相脉宽调制(pulse width modulation，PWM)整流器具备功率因数高、电流谐波含量低等特点[1]，因此被广泛应用于单相供电系统，如电力机车[2]、不间断电源(uninterruptible power supplies, UPS)[3]、新能源发电[4]等领域。整流器良好的控制性能是系统高效运行的必要条件。以改善系统稳态、动态性能为目标，国内外学者对电流控制策略展开了大量的研究，如瞬态控制[5]、比例谐振控制[6]、直轴交轴(direct-axis quadrature-axis, DQ)电流解耦控制[2]等[7]。其中，文献[5]中瞬态电流控制动态响应速度快，但比例积分(proportional-integral, PI)控制器难以精确跟踪50 Hz交流信号。文献[2]中DQ电流解耦控制因具备较好的稳态性能，在电力机车以及高速动车组中得以普遍应用，但动态响应速度较慢。

与以电流为系统状态变量的控制策略不同，功率控制策略将有功、无功功率作为系统状态变量。对比基于DQ电流解耦控制结构的各种电流控制，功率控制无需αβ/dq旋转坐标变换，即可得出瞬时功率信号(直流信号)，相当于在静态坐标系下，通过PI控制器能够实现无稳态误差的控制效果，且动态响应速度较快[8]。因此，近年来国内外学者对于PWM整流器功率控制策略的研究逐渐增多，常见的有滞环功率控制[9]、基于模糊规则的功率控制[10]、虚拟磁链功率控制算法[11]、传统功率前馈解耦控制[12]、无差拍功率控制[13]、模型预测功率控制[14]。其中，滞环功率控制算法简单且功率响应速度快[9]。文献[10]中控制策略通过模糊规则选择开关状态，动态性能较好，且网侧电流谐波少。上述两种算法均无法固定开关频率，因此不易设计电力滤波器。虚拟磁链功率控制取消网压传感器，提高了系统可靠性，降低了系统硬件成本，但存在积分漂移问题[11]。文献[12]在功率前馈解耦控制中，采用空间矢量脉宽调制技术实现了开关定频控制[12]，稳态性能较好，但动态性能尚不理想。无差拍功率控制策略动态性能较优，但控制系统需具备较高的采样频率，且被控对象参数准确性对控制效果影响大[13]。前文所述功率控制策略在系统动态、稳态性能方面有所提升，然而，控制结构普遍采用传统功率前馈解耦控制框架，只能得出网侧电压d、q轴电压分量。为获取输入到整流器的电压调制信号，仍需αβ/dq旋转坐标逆变换，控制结构稍显繁琐，限制了系统动态性能进一步提升。

此外，以上控制策略均未考虑整流器电路参数摄动对系统控制性能的影响。受外界因素影响，系统数学模型存在参数失配现象，其中，网侧等效电感参数摄动影响较大[15]。具体表现为：网侧电流波动幅度变大，调制信号失真，功率因数下降[16]。文献[14]提出的模型预测功率控制通过增加电感参数误差在线估计环节来改善系统鲁棒性，使电感参数变化时有功、无功功率波动平滑。H∞输出反馈控制算法在频域上通过加权函数约束跟踪精度、抗干扰等性能，利用状态空间描述，进而求解H∞控制问题[17]。在允许的参数摄动范围内系统控制效果与标称情况差别较小，设计结果更接近工程实际，是增强系统鲁棒性的有效解决方案。迄今为止，基于H∞的鲁棒控制算法，如H∞混合灵敏度控制[15]、H∞重复控制[18]等，已成功应用于PWM整流器领域，有效增强了整流器系统鲁棒性。但现有H∞鲁棒控制方法均针对电流控制结构，基于功率控制结构的H∞鲁棒控制算法对于PWM整流器的研究仍鲜有报道。

对此，本文为提升单相PWM整流器系统动态性能，提出了一种基于比例积分的改进型直接功率控制策略(proportional-integral modified direct power，PI-MDP)，取消了αβ/dq旋转坐标逆变换，简化了控制结构。在PI-MDP控制结构的基础上，为增强系统鲁棒性，提出了H∞改进型直接功率(H∞modified direct power，H∞-MDP)控制策略。相比于其余2种基于PI控制的功率控制策略，所提算法动态性能好、鲁棒性强。本文通过半实物实验平台，对传统功率前馈解耦控制策略、PI-MDP控制策略、H∞-MDP控制策略开展实验对比研究，验证了所提控制策略能有效应用于整流器系统。

1 单相PWM整流器功率数学模型

单相PWM整流器拓扑结构，如图1所示。图1中：网侧电压、网侧电流分别由us、is表示；L为网侧等效电感；R为网侧等效电阻；uab表示整流桥网侧输入电压；RL表示直流侧等效负载；Cd表示直流侧支撑电容；udc为直流侧电压。

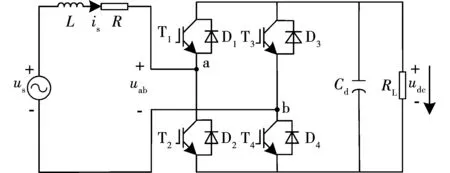
图1 单相PWM整流器拓扑结构Fig.1 Topology of the single-phase PWM rectifier

图1网侧电压动态平衡方程[7]为

(1)

单相系统仅能采样us、is标量值，为获取瞬时有功、无功功率信号，此处需选取二阶广义积分算法(second order generalized integrator,SOGI)构建虚拟αβ分量[14]。

忽略高次谐波，由SOGI构造的αβ坐标系下网侧电压、网侧电流αβ分量可表示为：

(2)

(3)

式中：usα、usβ、isα、isβ分别表示us、is的α、β坐标分量；usm、ism分别表示us、is幅值；φ为us与is的相位差；ω为us基波角频率。

定义系统瞬时有功功率P、无功功率Q表达式[14]为：

(4)

2 单相PWM整流器功率控制策略

2.1 传统功率前馈解耦控制策略

传统功率前馈解耦策略功率环数学模型[12]可表示为：

(5)

式中：uabd、uabq为uab的d、q分量；P*、Q*分别表示给定有功功率、给定无功功率；KPp、KPi、KQp、KQi分别表示有功、无功PI控制器的比例、积分系数。设定两PI控制器参数一致，以实现对P、Q的同步控制。

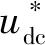
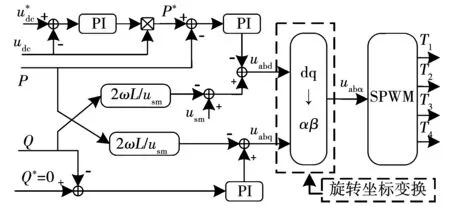
图2 传统功率前馈解耦控制框架Fig.2 Traditional power feedforward decoupling control frame

2.2 基于PI的改进型功率(PI-MDP)控制策略

根据式(4)可得有功功率P、无功功率Q对时间t的微分表达式为：

(6)

联立式(1)、式(2)、式(3)，可将图1在αβ坐标系下网侧电压动态平衡方程表示为：

(7)

式中uabβ表示整流桥网侧输入电压uab的β分量。

将式(2)、式(7)代入式(6)，可得：

(8)

式中uP、uQ分别定义为有功电压调制信号、无功电压调制信号。

联立式(2)、式(8)，可得

(9)

注意到式(9)中右侧三角函数矩阵，即为整流器DQ电流解耦控制结构中的αβ/dq坐标变换关系[9]。根据电流控制中αβ/dq坐标逆变换矩阵关系可得

(10)

将式(10)中1/usm分子分母同时乘以usm，并联立式(2)，整理可得

(11)

式中uabα即为整流桥电压调制输入信号。

为求取式(11)中uabα，需得出未知电压调制信号uP、uQ。分别定义整流器改进型功率系统有功、无功控制器输出信号为vP、vQ表达式为：

(12)

联立式(8)、式(12)，可得改进型功率环标称数学模型为：

(13)

根据式(13)，可知功率环状态空间表达式为：

(14)

式中GNP、GNQ分别表示有功、无功标称模型。

功率标称模型闭环控制框图，如图3所示。图3中：eP、eQ分别为有功功率、无功功率跟踪误差；KP、KQ分别为待设计有功功率、无功功率控制器。由图3可知，eP、eQ分别经功率控制器KP、KQ输出即为式(13)中vP、vQ[15]。

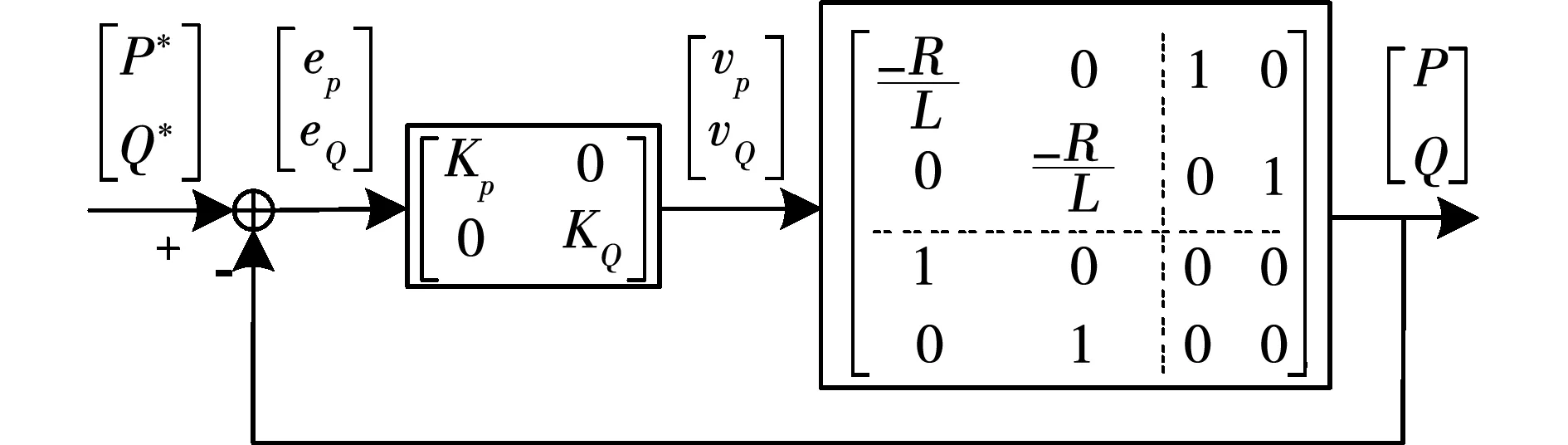
图3 功率标称模型闭环控制框图Fig.3 Closed-loop power nominal model block diagram

根据式(12)，可将uP、uQ表示为：

(15)

由此，可得基于PI-MDP控制结构，如图4所示。相比于传统功率前馈解耦控制策略，基于PI-MDP控制策略无需αβ/dq旋转坐标逆变换，即可得出整流桥调制输入信号uabα，控制系统结构更为简便，可进一步增强该系统动态性能。

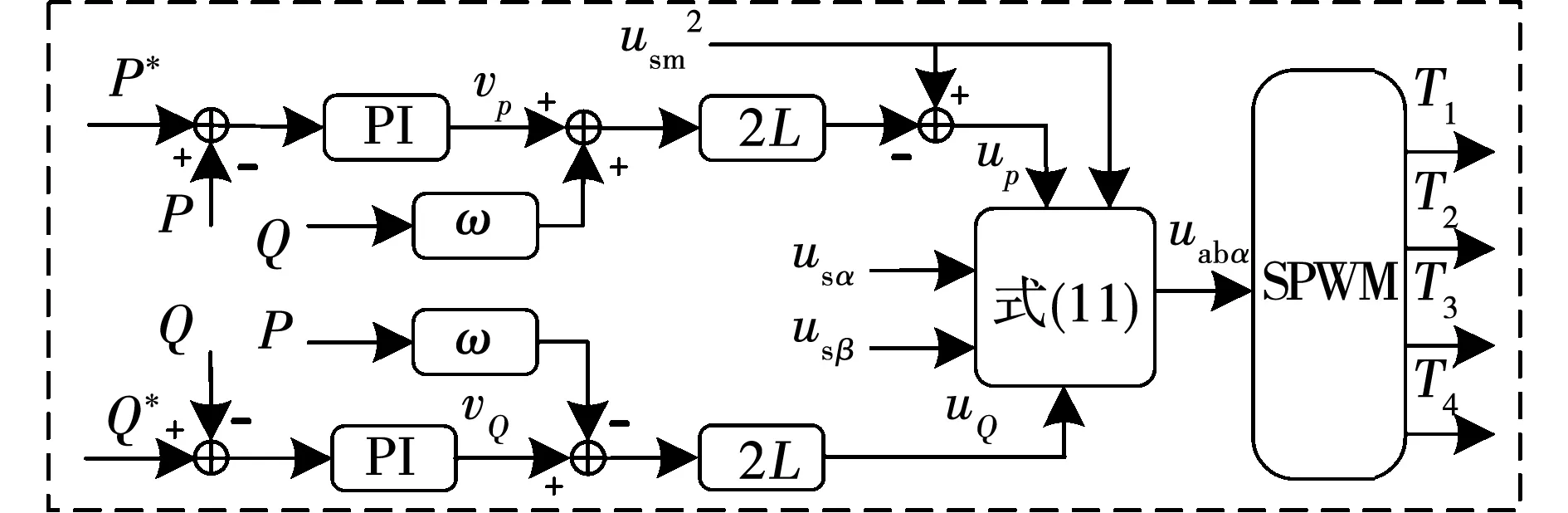
图4 基于PI-MDP控制框图Fig.4 Block diagram of PI-MDP

3 H∞-MDP控制策略

3.1 H∞输出反馈控制问题

为增强整流器系统在参数摄动情况下的鲁棒性，利用H∞输出反馈控制器取代图4中功率环PI控制器，该算法对由标称模型GNP、GNQ以及性能加权函数所构成的广义受控对象进行控制器设计。

由式(14)可知，整流器功率环标称模型GNP、GNQ参数一致，且控制系统通常设置有功、无功控制器相同。为方便后文表述，下文仅对有功功率控制器KP进行分析。

根据式(14)可知，整流器功率数学模型由R、L确定。R对系统控制性能影响较小，可忽略。设L摄动范围为[-30%,30%]，其乘性不确定表达式GP为[15]：

(16)

式中：I表示单位矩阵，||Δ||∞≤1；WP为乘性不确定加权函数。

功率环广义控制结构，如图5所示。图5中：dP为外界干扰；ZeP、ZuP分别表示系统跟踪性能、控制能量评价输出；WeP表示跟踪精度加权函数；WuP表示控制输出加权函数。

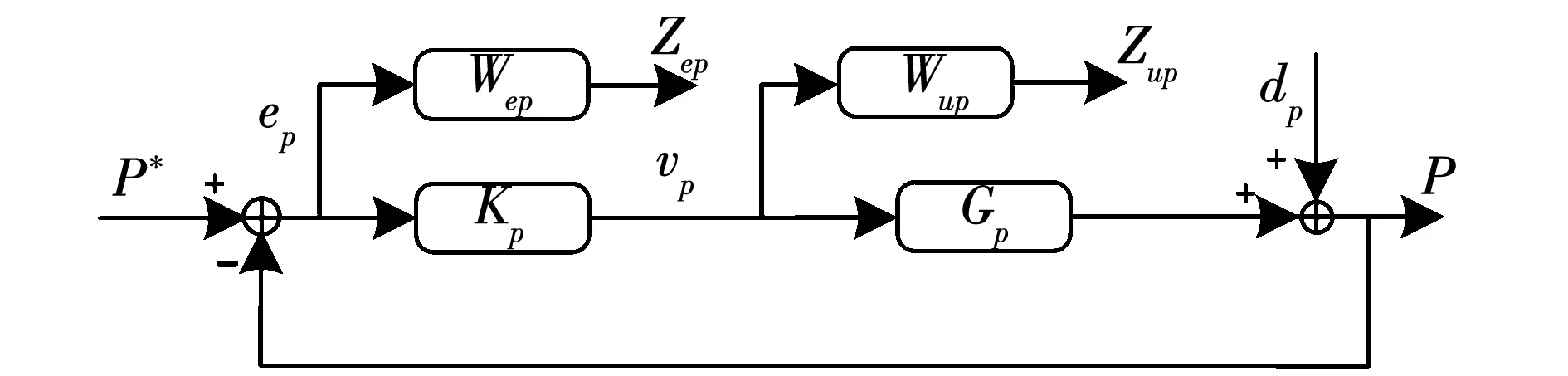
图5 功率环广义控制结构Fig.5 Power-loop generalized control structure

定义P*到eP传递函数为灵敏度函数S(s)，如下式所示。根据图5可知，S(s)也可表示dP到P的传递函数，存在

S(s)=eP(P*)-1=P(dP)-1=(I+GPKP)-1。

(17)

设控制系统外部输入ωi由P*与dP构成，外部输出Zo由ZeP与ZuP构成。由此，图4中考虑加权函数的H∞输出反馈控制框架，表达式为：

(18)

式中PP表示广义被控对象状态矩阵，其表达式为

(19)

为降低H∞输出反馈控制器阶次，便于硬件实现，选取性能加权函数WeP、WuP为一阶传递函数，表达式为[19]：

(20)

式中a、b、c、d、g、h分别表示加权函数WeP、WuP系数。

通过计算，可得式(18)中广义被控对象状态矩阵PP及其标准化状态空间表达式为

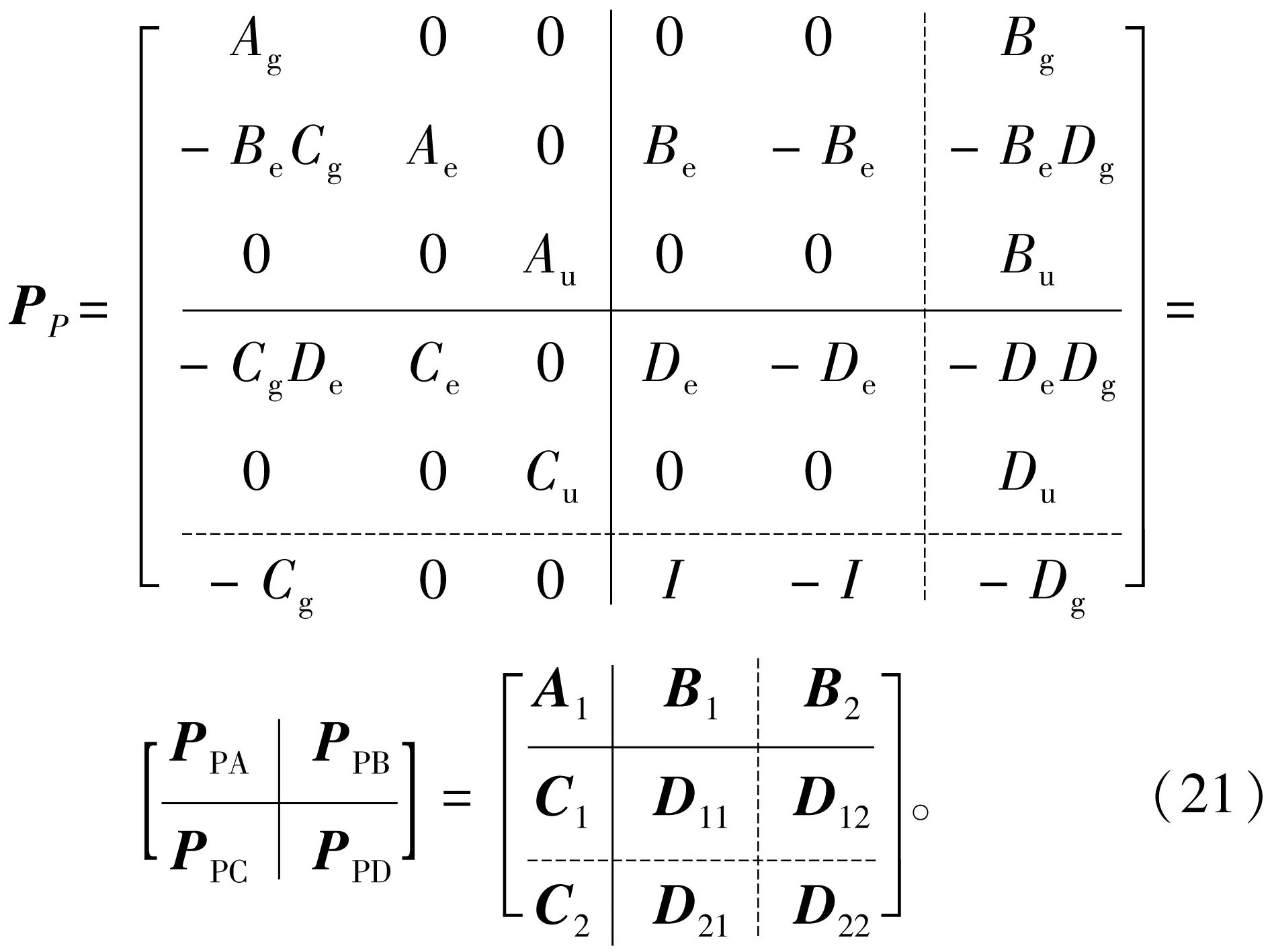
式中Ag、Bg、Cg、Dg为GP的状态空间矩阵。

单相PWM整流器功率环H∞输出反馈控制问题可描述为[17]：针对广义被控对象PP，求取一反馈控制器KP使得‖Tzω(s)‖∞<1，并满足闭环系统内稳定条件。其中，Tzω表示PP外部输入ωi到外部输出Zo的传递函数。利用线性分式变换这一数学工具[20]，可将Tzω记为Fl(PP,KP)。

3.2 H∞输出反馈控制器实现

H∞输出反馈控制算法利用加权函数在频域中对控制系统各项性能指标进行刻画。

WeP表征对S(s)的性能加权，S(s)越小，跟踪精度越高，抗干扰性越强。若S(s)幅值为-40 dB，则表示整流器功率跟踪误差为给定有功功率的1/100，且控制系统外界干扰信号到系统输出的影响被缩小100倍。系统输入功率信号为直流量，若在低频段S(s)越小，则跟踪误差越小。因此，WeP需具备低通特性[21]。

WuP表征对P*到vP的加权，可避免整流器系统在工作过程中的饱和现象。为符合系统鲁棒性要求[22]，WuP的倒数应大于S(s)KP。

由控制理论可知：带宽ωb高，对应动态性能越优。但带宽增大将导致控制系统超调量增加。此外，将整流器系统PWM开关频率表示为fpwm，网侧电流is的高次谐波含量分布在2fpwm附近[14]，由式(3)、式(4)可知，瞬时功率包含网侧电流is分量。系统带宽增大会削弱网侧电流高频谐波分量抑制能力。考虑控制系统超调量以及对网侧电流is高次谐波的抑制，设置系统带宽ωb<2fpwm。

综合上述选取依据，通过半实物验证后，确定各项系数，表达式为：

(22)

假设控制器KP状态空间表达式为

(23)

由此可得，广义被控对象外部输入ωi到输出Zo的传递函数Tzω，表达式为

PPA+PPBKP(I-PPDKP)-1PPC。

(24)

式中：

(25)

将式(22)代入式(20)获得加权函数状态空间。将表1所示标称参数代入式(14)，联立式(20)、式(21)，表示出PP各项矩阵。利用MATLAB鲁棒控制工具箱中函数“hinfsyn”，设置式(24)中范数‖Tzω(s)‖∞界为[0.1,10]，并基于黎卡提方程对H∞输出反馈控制问题进行滚动寻优[17]，求得H∞输出反馈控制器KP，表达式为：

(26)

所得结果显示‖Tzω‖∞值为0.953，小于1。根据小增益定理[23]，可知功率控制系统鲁棒稳定。

图6所示为H∞-MDP控制策略结构框图。图7给出了H∞输出反馈控制闭环幅频特性曲线、加权函数曲线、灵敏度函数曲线。根据图7以及表1开关频率fpwm可知，整流器系统带宽为2 897 rad/s，在预期带宽2fpwm内。曲线WeP<1/S(s)、S(s)KP<1/WuP，说明H∞输出反馈控制器可使单相PWM整流器系统满足跟踪精度、外界干扰、控制输出能量鲁棒性要求[22]。图7中，闭环幅频特性曲线GPKP/(I+GPKP)在低于带宽2 897 rad/s时幅值约为0 dB，表明控制系统对给定功率P*跟踪效果良好。灵敏度函数S(s)曲线频率低于200 rad/s范围时，幅值小于-20 dB，表示该控制系统对低于此频率值的外界干扰至少具有10倍抑制效果，在更低频率处，S(s)约为-66 dB，表明功率信号稳态误差可限制在1/1 000内。

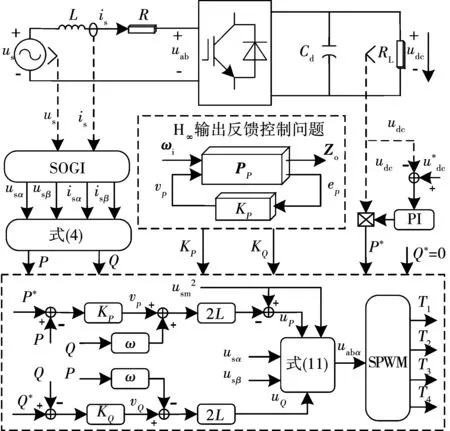
图6 H∞-MDP策略结构框图Fig.6 Structure of the H∞-MDP strategy

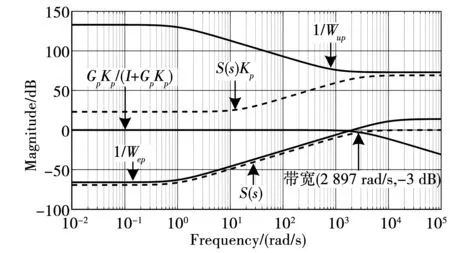
图7 H∞输出反馈控制闭环幅频特性曲线、加权函数曲线、灵敏度曲线Fig.7 Closed-loop amplitude-frequency curve, the weighting function curve and the sensitivity curve of the H∞ output feedback control

4 实验对比结果及分析

为验证所提H∞-MDP控制策略的有效性，通过dSPACE半实物平台对传统功率前馈解耦控制策略、基于PI-MDP控制策略、H∞-MDP控制策略开展实验对比研究。图8为单相PWM整流器实验平台。

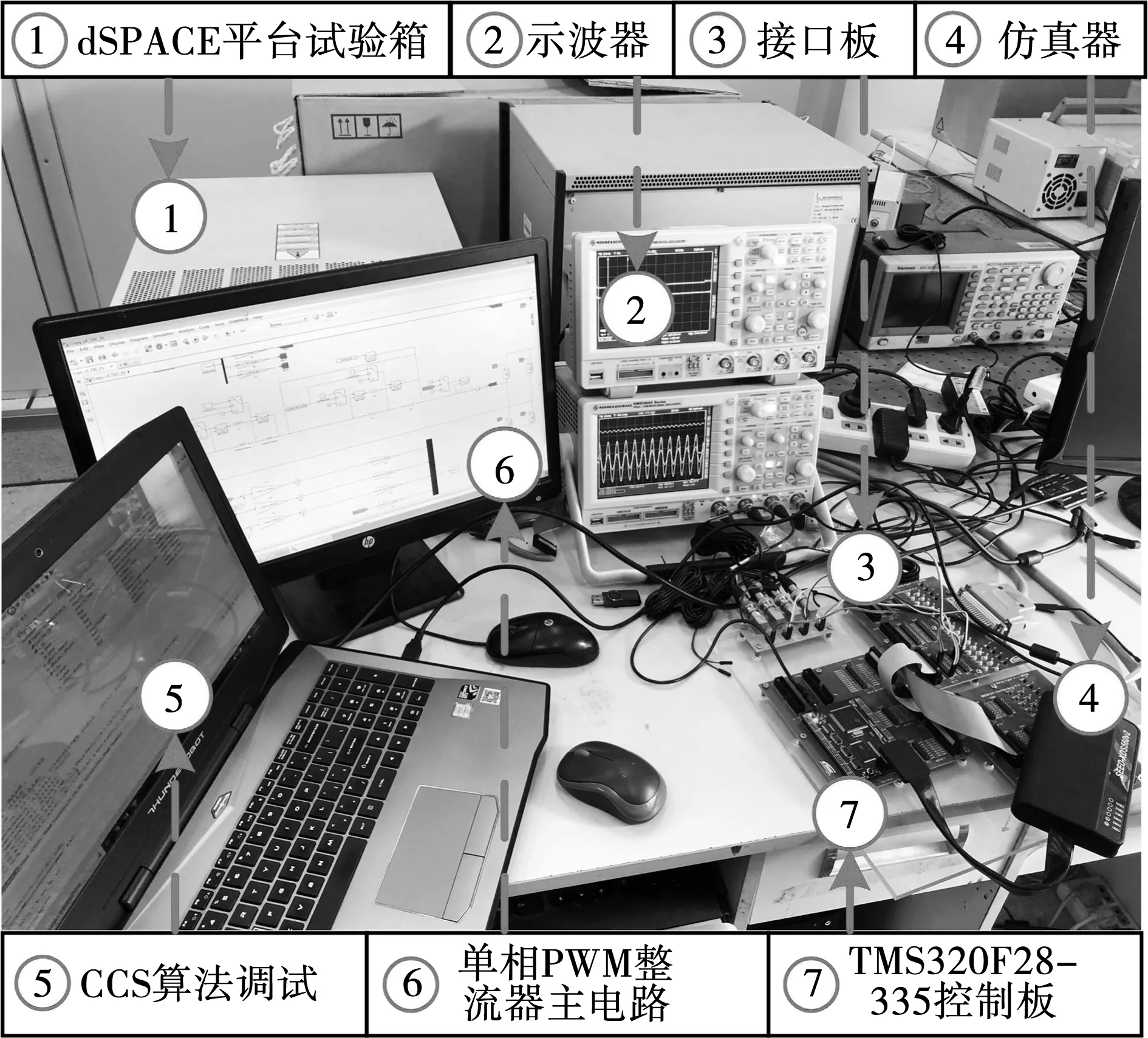
图8 单相PWM整流器实验平台Fig.8 Platform of the single-phase PWM rectifier

针对基于PI控制方法的两种功率控制策略，在实验调试过程中，先根据给定有功功率突变时动态响应效果确定内环P、I参数，再由负载突变时直流侧电压响应效果确定外环P、I参数，进行实验到微调再到实验的参数整定。为公平对比功率环动态性能，3种控制策略电压环采用相同参数。表1所示为单相PWM整流器实验系统参数。

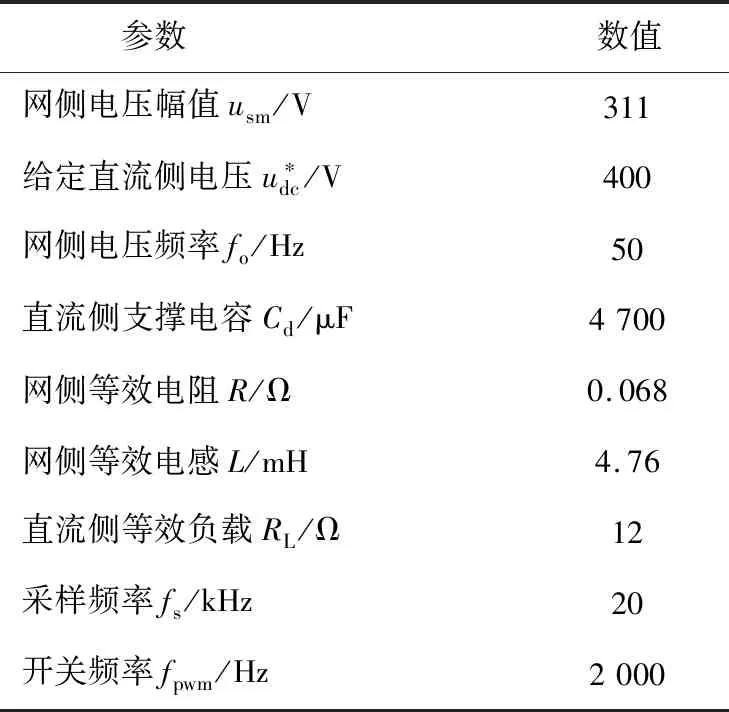
表1 单相PWM整流器实验系统参数Table 1 System parametersof the single-phase PWM rectifier

本文研究对比了4种工况，其中工况1为稳态性能；工况2、3为动态性能；工况4为鲁棒性能。

1)工况1：图9给出了整流器系统处于稳态情况下，3种功率控制策略udc、us、is实验波形。由图9可以看出，3种控制策略udc恒定，us与is相位重合。表2为系统处于稳态情况下，3种功率控制策略is的FFT分析结果。由表2可知，3种策略的is谐波含量基本一致。工况1对比结果说明基于PI-MDP控制策略与H∞-MDP控制策略可实现与传统功率前馈解耦控制策略同样优越的稳态性能。文中所设计H∞输出反馈控制器能有效应用于单相PWM整流器系统。

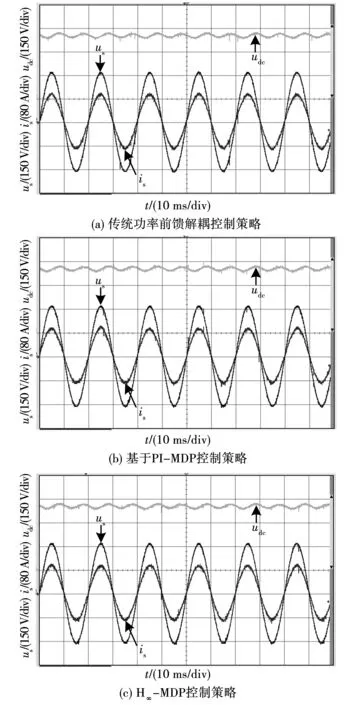
图9 稳态情况下，直流侧电压、网侧电压、网侧电流Fig.9 Experimental waveforms of udc,us and is in steady-state condition

表2 稳态情况下，网侧电流FFT分析结果Table 2 FFT results of is in steady-state condition

2)工况2：图10给出了3种功率控制策略在给定有功功率P*从15 kW突变到20 kW情况下，P*、P、Q、is实验波形。由图10可知，三种功率控制P调节时间分别为18、8、5 ms。基于PI-MDP控制策略调节时间比传统功率前馈解耦控制调节时间短10 ms，说明采用改进型功率控制结构，改善了系统动态性能。同时，相比于基于PI-MDP控制策略，所提H∞-MDP控制策略动态性能略有提升。

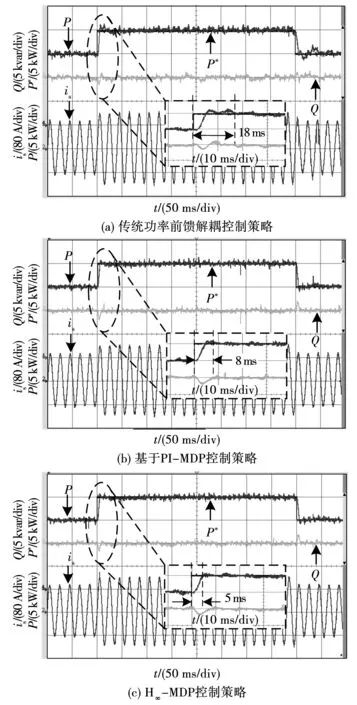
图10 给定有功突变情况下，给定有功功率、有功功率、无功功率、网侧电流Fig.10 Experimental waveforms of P, P*,Q,is in active reference power steps change condition

3)工况3：图11给出了RL从24 Ω突变到12 Ω情况下，3种功率控制策略udc、is、P、Q实验波形。由图11(a)可观察出，传统功率前馈解耦控制策略的直流侧电压恢复到稳态值所需调节时间约为85 ms，而图11(b)采用基于PI-MDP控制策略的直流侧电压调节时间约为75 ms。对比结果说明，改进型控制结构在动态性能方面具有较好的控制效果。图11(c)采用H∞-MDP控制策略的调节时间约为66 ms。工况3实验结果显示H∞-MDP控制策略电压外环动态性能相比2种基于PI控制器的功率控制策略较优。

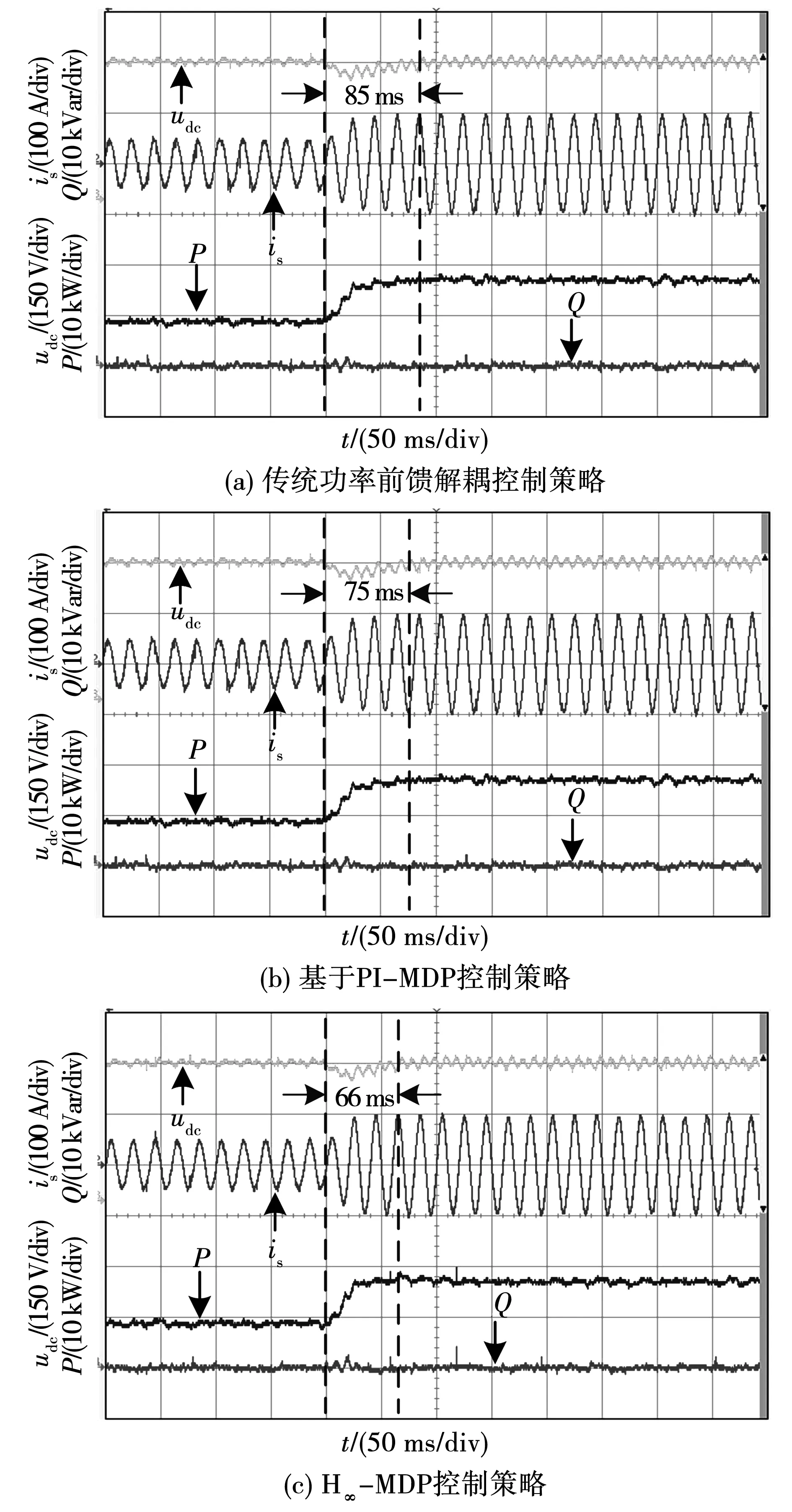
图11 负载突变时，直流侧电压、网侧电流、有功功率、无功功率Fig.11 Experimental waveforms of udc,is,P,Q in load sudden change condition

4)工况4：图12给出了RL恒定情况下，L参数突变20%时，3种功率控制策略的is、udc、P、Q实验波形。根据图12实验波形，将工况4实验对比结果在表3给出。由表3可知在L摄动情况下，基于PI-MDP控制策略系统鲁棒性优于传统功率前馈解耦控制策略。H∞-MDP控制策略对应的P、Q波动峰峰值均小于其余2种基于PI控制器的功率控制策略，所提H∞-MDP控制策略能有效提升整流器系统鲁棒性。

表3 工况4电感参数突变时，功率波动实验对比Table 3 Comparison results in condition 4

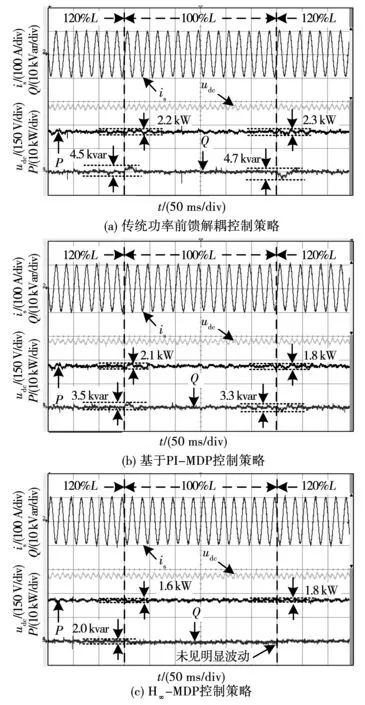
图12 额定负载情况下，网侧等效电感突变时，网侧电流、直流侧电压、有功、无功功率Fig.12 Experimental waveforms of is,udc, P, Q in equivalent inductance sudden change with RL

表4给出了在4种工况下的控制策略实验对比结果。

表4 4种工况下的实验对比结果Table 4 Experimental comparison results under 4 conditions

5 结 论

本文为提升单相PWM脉冲整流器系统动态以及鲁棒性能，提出了一种H∞-MDP控制策略。所提控制策略取消了αβ/dq旋转坐标逆变换，仅在基于PI-MDP控制结构的基础上改变功率PI控制器，实现简便。通过半实物实验平台对H∞-MDP、传统功率前馈解耦、基于PI-MDP的3种控制策略开展了实验对比研究，可得如下结论：

1)基于PI-MDP控制策略与H∞-MDP控制策略可实现与传统功率前馈解耦控制策略同样优越的稳态性能。

2)基于PI-MDP控制策略系统动态响应性能优于传统功率前馈解耦控制策略，但略次于所提H∞-MDP控制策略。

3)与2种基于PI控制器的功率控制策略相比，所提H∞-MDP控制策略有效增强了整流器系统在网侧电感参数摄动情况下的鲁棒性。

相对于传统控制前馈解耦控制策略，所提算法虽然取得了较好的控制效果，但注意到该方法电压环在负载突变时，调节时间为66 ms，仍然较慢。如何设计出电压环与电流环统一控制框架，并通过H∞输出反馈功率控制策略，进行单相PWM整流器双闭环动态性能改善，将是未来工作研究的重点。