面向谐波和电压综合治理的电压检测型APF 与SVG 协同配置

田书娅，贾清泉，林丽娟，赵 静，崔屹峰，于 浩

（1. 电力电子节能与传动控制河北省重点实验室（燕山大学），河北省秦皇岛市 066004；2. 河北交通职业技术学院电气与信息工程系，河北省石家庄市 050035；3. 国网黑龙江省电力有限公司电力科学研究院，黑龙江省哈尔滨市 150030）

0 引言

随着分布式电源（DG）的高渗透和电力电子设备的广泛应用，现代配电网电力电子化特征愈加显著［1-2］，电网谐波污染更加严重［3］。同时，DG 的随机性和间歇性使得配电网电压分布更复杂，电压偏差问题更严重，治理难度加大［4］。由此可见，电力电子化配电网中谐波和电压问题严重，污染源呈现高密度、分散化、全网化特点，按照“谁污染谁治理”原则的传统用户侧点对点治理模式不能满足需要。因此，探索一种从电网侧对电力电子化配电网中分散化、全网化的电能质量污染进行治理的新手段十分必要［5］。

电流检测型有源滤波器（CDAPF）以谐波源负荷馈线为治理目标，通过检测谐波源馈线电流注入等幅反向的谐波电流，即可达到控制全网谐波水平的目的，主要适用于传统电网点对点治理模式，用于电力电子化配电网中的分散谐波治理则具有局限性［6］。电压检测型有源滤波器（VDAPF）以节点谐波电压为治理目标，根据检测电压并结合设定的电导值计算出有源滤波器（APF）补偿电流来削弱VDAPF 接入点的谐波电压，从而使接入点及其附近区域的电压畸变得到治理。单个VDAPF 可治理一定区域污染，多个VDAPF 可构成分布式治理系统对整个电网实施治理。可见，VDAPF 与CDAPF相比，更适合对电力电子化配电网中分散化、全网化的谐波污染进行治理。

目前关于VDAPF 治理谐波的研究已取得一定成果［7-12］。VDAPF 最初应用于抑制线路的谐波谐振［7-8］。文献［9］指出在馈线末端安装VDAPF 能够有效抑制谐波电压的传播。文献［10］提出一种基于分频控制的VDAPF 位置选择方案。文献［11］提出基于VDAPF 的全局优化与本地分区治理相结合的策略，实现了谐波分布式协同治理。在此基础上，文献［12］分析了VDAPF 控制参数对分布式谐波治理系统稳定性的影响。此外，VDAPF 还兼具无功补偿功能。因此，在保证VDAPF 满足谐波治理需求的前提下，可以利用其剩余容量治理电压偏差。而且，谐波和电压偏差分布的不确定性使两种污染并非总是同时最严重，VDAPF 在大多数场景下均可参与电压治理。由于VDAPF 只是辅助治理电压偏差，仅利用其剩余容量并不能满足全网电压偏差治理需求，因此仍需安装一定容量的无功补偿设备，如静止无功发生器（static var generator，SVG）［13］，对电网中DG 大规模接入引起的电压偏差污染进行治理。VDAPF 接入容量不同，其剩余容量对电压偏差的治理程度不同，导致SVG 接入容量不同，从而产生不同的投资费用及治理效果。研究如何系统化协同配置VDAPF 和SVG，对降低系统投资成本、全面改善谐波和电压偏差综合治理性能、实现治理效果和经济性双重目标，具有重要意义。文献［14］采用反函数抛物线插值确定滤波器配置容量。文献［15］建立以配电网各节点电压谐波含量、APF 总安装台数及安装容量为目标的APF 优化配置模型，并采用多目标粒子群及单目标迭代算法求解。文献［16］采用灰狼优化器求解APF 最佳安装位置和容量。文献［17］建立以系统有功网损最小、设备补偿费用最低、系统电压稳定性最好为目标函数的可控串联补偿装置（TCSC）和SVG 优化配置模型，并采用改进差分和声搜索算法求解。文献［18］提出一种电容器与SVG 综合优化配置方法。然而，上述研究基本都是从不同优化目标、不同优化求解算法等方面入手，主要围绕谐波和电压偏差问题进行单类设备配置，并未考虑结合多种治理设备综合治理谐波和电压偏差，导致污染较轻时治理设备部分容量被闲置。

本文提出一种面向谐波和电压综合治理的VDAPF 与SVG 协同优化配置策略。采用分区治理思想，提出基于社团结构理论的综合电能质量分区方法，选取区域主导节点为VDAPF 和SVG 提供候选接入节点。在此基础上，以系统总投资费用最小和电能质量水平最优为目标函数，建立多目标VDAPF 和SVG 协同优化配置模型。针对所建优化模型的特点，采用规格化平面约束（normalized normal constraint，NNC）法结合改进的粒子群优化（PSO）算法求解。最后，采用IEEE 33 节点系统验证所提方法的有效性。

1 谐波和电压偏差综合分区治理

本文采用分区治理方式将网络划分为不同区域后，选取各区域的主导治理节点作为VDAPF 和SVG 的候选节点对电网谐波和电压偏差进行治理。以两节点之间的综合电压灵敏度作为综合分区指标对网络进行分区，依据区域内节点的谐波灵敏度、无功灵敏度和综合灵敏度分别选取区域的主导治理节点，形成候选节点集合。该分区治理方法从规划层面保障了谐波和电压偏差治理的区域化，保证了候选节点的有效性。

1.1 基于综合电压灵敏度指标的分区方法

配电网中节点ij之间基波电压/无功灵敏度Sij如式（1）所示，其值可通过潮流计算中雅可比矩阵的逆矩阵求得［19］。

式中：Vi和Qj分别为节点i的基波电压和节点j的无功功率。

节点间基波电压关系可描述为：

式中：ΔVi为节点i的基波电压变化量；αij为节点ij之间基波电压灵敏度。

在特定频率下，VDAPF 的谐波治理是通过改变其等效电导实现的［11］。因此，本文以节点VDAPF 等效电导的增量对其余各节点谐波电压的治理程度来表示谐波灵敏度，并将其作为区域主导节点选取的依据，以保证主导节点的有效性。节点ij之间h次谐波灵敏度Eh，ij如式（3）所示。

式中：Vh，j为节点j的h次谐波电压；Gh，i为节点i处接入的VDAPF 的h次谐波的等效电导。

将节点ij之间总谐波灵敏度Eij定义为各次谐波灵敏度的均方根，如式（4）所示。

式中：N和H分别为谐波个数和最大谐波次数。

VDAPF 并网后的谐波潮流方程如式（5）所示，可知治理设备的等效电导Gh，i包含在系统h次谐波导纳矩阵Yh的对角元素里。节点i的h次谐波注入电流Ih，i是已知量，可通过历史数据预测获取，因此，Vh，i是等效电导Gh，i的因变量，利用式（5）可求得各节点的谐波灵敏度。

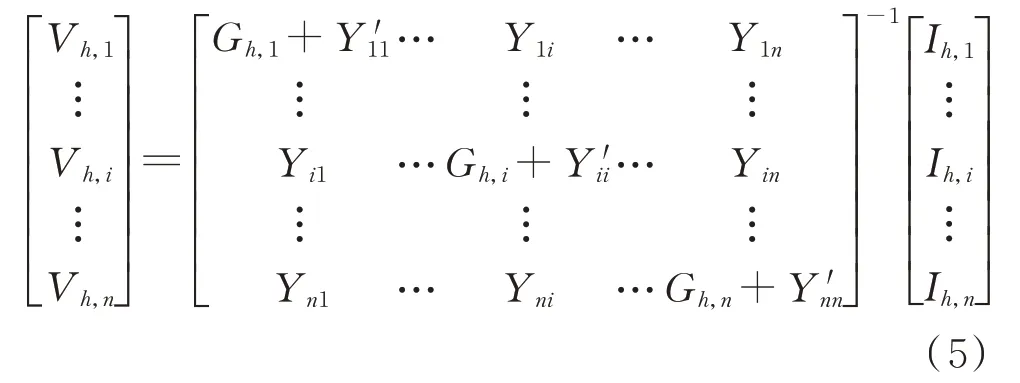
式中：Yi′i为不包含Gh，i部分的节点i的自导纳；Yin为节点i和节点n之间的互导纳；n为网络节点总数。

节点间h次谐波电压的关系可表示为：

式中：ΔVh，i为节点i的h次谐波电压变化量；γh，ij为节点ij之间h次谐波电压灵敏度。

节点ij之间的总谐波电压灵敏度γij以均方根形式进行定义，如式（7）所示。

为了实现谐波和电压问题的综合分区治理，将谐波电压灵敏度和基波电压灵敏度的加权形式定义为综合电压灵敏度指标ζij，并根据两种污染的严重程度赋予相应的权重系数，以便在分区过程中更好地体现污染的严重程度，如式（8）所示。

式中：α′ij和γ′ij分别为归一化后的αij和γij；τ为权重系数；DTH，i和DAV，i分别为节点i的谐波电压畸变率和电压偏差绝对值。

依据综合电压灵敏度指标，文中采用基于模块度Qmod函数的Louvain 社团发现算法将网络划分为不同的区域。与其他分区算法相比，该算法能依据Qmod最大值自动生成最佳分区数目而不需要提前设定，并且能够发现层次性的社区结构［20］。

模块度Qmod的表达式为：

1.2 VDAPF 和SVG 候选节点的确定

将网络划分为不同的区域后，选取各区域的主导治理节点作为VDAPF 和SVG 的候选接入节点。主导治理节点的电能质量污染得到治理的同时，同一区域内其余节点的电能质量污染也会有最大程度的改善。可见，主导治理节点对其余节点具有较强的可控性。因此，将谐波灵敏度Eij和基波电压/无功灵敏度Sij作为可控性指标，并通过计算上述指标的最大平均值确定区域内的主导节点，为治理设备提供更加有效的候选安装位置。

依据灵敏度指标Eij选取区域内谐波的主导治理节点作为VDAPF 的候选接入位置，如式（10）所示。依据灵敏度指标Sij，按照式（11）选取电压偏差的主导治理节点作为SVG 的候选接入节点。

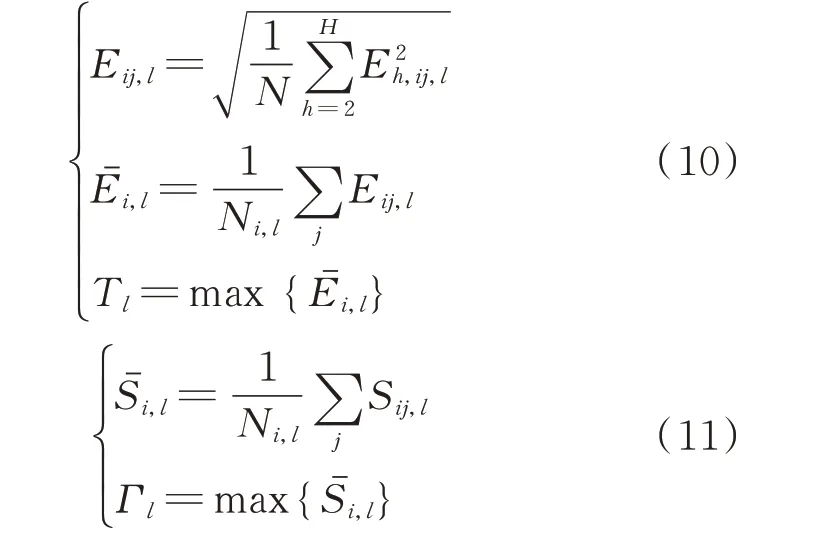
式中：Ni，l为第l个区域内与节点i连接的节点数；Eh，ij，l和Eij，l分别为第l个区域内节点ij间的h次谐波灵敏度和总谐波灵敏度；Sij，l为第l个区域内节点ij间的基波电压/无功灵敏度；Eˉi，l和Sˉi，l分别为第l个区域内节点i的平均谐波灵敏度和平均基波电压/无功灵敏度；Γl和Tl分别为第l个区域内Sˉi，l和Eˉi，l的最大平均值。

由于VDAPF 的剩余容量可以进行无功补偿，因此，定义体现主导节点对其余节点可控性的综合灵敏度Wij，l如式（12）所示，并依据该指标选取综合治理谐波和电压偏差的主导治理节点作为VDAPF的候选节点，如式（13）所示。

式中：Zl为第l个区域内节点的综合灵敏度最大值；E′h，ij，l和S′ij，l分别为归一化的Eh，ij，l和Sij，l，归一化所用方法参考文献［21］中的min-max 规范化方法；η为Eij，l的重要程度。

2 VDAPF 和SVG 协同优化配置模型

2.1 目标函数

为了充分挖掘治理设备的成本和功能优势，分别以VDAPF 和SVG 的年投资费用最小和电能质量水平最优为目标，建立多目标的VDAPF 和SVG协同优化配置模型。

年投资费用最小目标函数可表示为：

式中：Cl为第l个区域内治理设备的年投资费用；K为网络总分区数量；IVF，t和ISG，x分别为第l个区域内第t个安装节点处VDAPF 和第x个安装节点处SVG 的接入容量；Ml和Xl分别为第l个区域内VDAPF 和SVG 的安装节点数；RVF、RSG、R为治理设备的等年值系数；r和L分别为治理设备的折旧率和使用寿命；cVF和cSG分别为VDAPF 和SVG 的单位容量成本。

电能质量水平最优目标函数可表示为：

式中：Dl为第l个区域内所有节点的总电能质量水平。

2.2 约束条件

1）系统功率平衡潮流方程

式中：Pz，i和Qz，i分别为节点i注入的有功和无功功率；ΔPi-1，i和ΔQi-1，i分别为节点i与i-1 间的线路有功和无功功率损耗；PL，i和QL，i分别为节点i负荷的有功和无功功率；QVF，i和QSG，i分别为设备VDAPF 和SVG 的注入无功功率；λi和γi为二进制决策变量，值为1 表示节点i接入对应设备，反之为0。

2）系统谐波潮流方程

式中：Vh和Ih分别为节点谐波电压和节点注入的谐波电流列向量。

3）各节点治理设备的安装容量约束

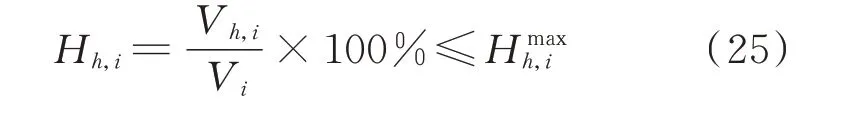
式中：Vmini和Vmaxi分别为节点i的基波电压最小值和最大值；为节点i的最大谐波电压畸变率；Hh，i和分别为节点i的谐波电压含有率及其最大值。

2.3 求解算法

本文建立的协同优化配置模型中总投资费用最小和电能质量水平最优两目标函数处于相互竞争关系，不存在唯一最优解。为了能获得均匀分布的Pareto 最优解集，本文采用NNC 法［22］求解多目标优化模型，以得到多种不同水平的配置方案，进而决策者可根据不同的系统需求选出合适的折中最优解作为最终配置方案。

NNC 法具体求解步骤如下。

步骤1：将建立的多目标优化配置模型划分为两个单目标优化模型，并以式（19）至式（25）构建等式约束和不等式约束，分别求解得到各自的最优解(fmin1，fmax2)和(fmax1，fmin2)。

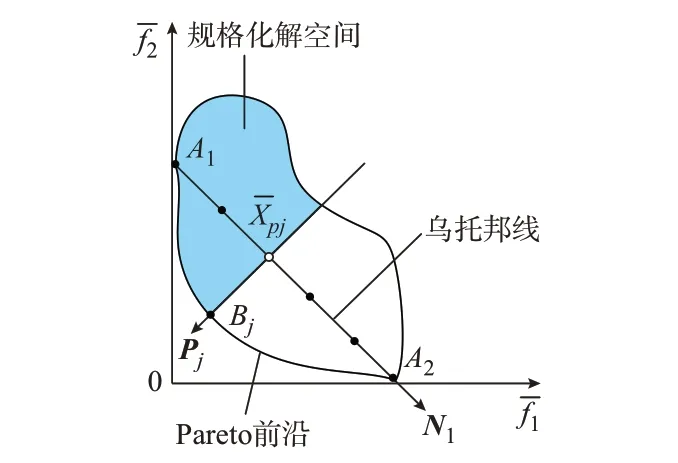
图1 多目标优化问题的规格化解空间Fig.1 Normalized solution space for multi-objective optimization problem

步骤3：将乌托邦线a等分，产生a+1 个等分点。

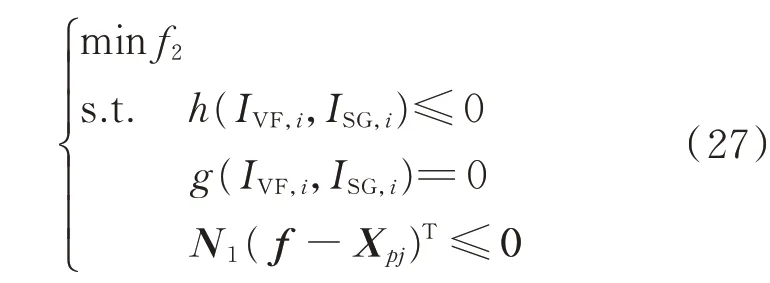
式中：g(·)=0 和h(·)≤0 分别表示式（19）至式（25）描述的等式约束和不等式约束。

引入不等式N1(f-Xpj)T≤0 后，新的单目标优化模型的解空间缩小为图1 中的上半部分区域。对每一个分割点求解新模型后，即可得到均匀分布的Pareto 最优解集。

与此同时，考虑到改进PSO 算法［23］容易实现、精度高、调节参数少，文中采用该算法求解构建的非线性单目标优化模型。

3 算例结果与分析

本文以IEEE 33 节点网络［24］为参考模型验证所提策略的有效性。系统线路和负荷参数参考文献［24］。设在节点8、17、24、32 处分别接入额定容量为0.8、0.6、0.9、1.0 MW 的DG。考虑到DG 出力和负荷不确定性对电压分布的影响，分别依据现有的光伏出力与负荷的概率模型获取不同运行场景下DG 出力和负荷的分布情况，模型参数见文献［25］。同时，为反映谐波污染源的分散化和全网化特点，基于文献［26-27］中DG 和负荷的谐波源等效模型，随机产生32 个节点的5、7、11、13 次谐波电流。以每小时为一个运行场景，构建一年8 760 个运行场景研究VDAPF 和SVG 的最佳接入位置和容量。某一典型时刻下各节点谐波注入电流见附录A 图A1。

3.1 分区方案及主导节点选取结果

利用Louvain 分区算法对33 节点网络进行区域划分。图2 描述了模块度Qmod值与分区数目的对应情况，可以看出Qmod最大值为0.594，其对应的分区数目为5。因此，系统的最佳分区为5。

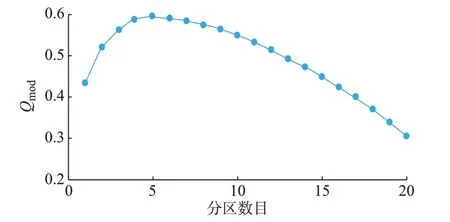
图2 Qmod和分区数量的关系Fig.2 Relationship between Qmod and region numbers

系统最优分区结果如附录A 图A2 所示。由图A2 可知，系统被划分为5 个区域，各区域主导节点选取结果如表1 所示。

表1 区域主导节点选择结果Table 1 Results of dominant node selection in each region

VDAPF 候选接入节点由基于灵敏度Eij，l和综合灵敏度Wij，l确定的主导节点共同组成。由表1 可知，VDAPF 候选节点为8、16、17、20、21、23、25、31、32。SVG 候选接入节点只由依据灵敏度指标Sij，l确定的主导节点组成，因此，其候选节点为9、17、21、24、32。

3.2 VDAPF 和SVG 最佳选址和定容

采用NNC 法求解文中提出的协同优化配置模型时，取a=18，求解得到19 个Pareto 前沿点，共对应19 种不同投资费用和电能质量水平的配置方案，如图3 所示。在获得Pareto 最优解集后，采用熵权法［28］从Pareto 前沿点中筛选出一个折中最优解，为研究人员决策提供参考。通过计算，得到j=10 时取得折中最优解。由图3 可知，选取的折中最优解使目标函数f1和f2同时取得较小值，说明该配置方案的经济性和电能质量治理效果均达到较优水平。

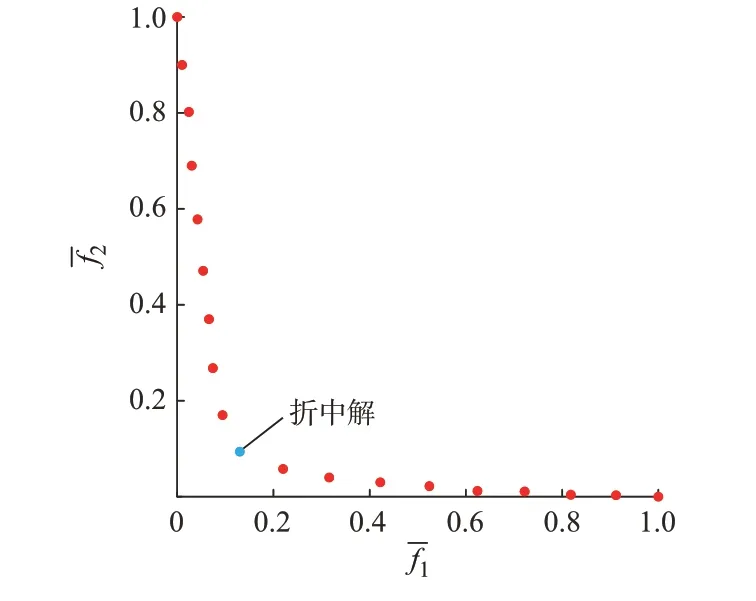
图3 NNC 法获得Pareto 最优解集和折中最优解Fig.3 Pareto optimal solution sets obtained by NNC algorithm and compromised optimal solution

表2 给出了选取折中最优解下VDAPF 和SVG的优化配置结果。由表2 可知，所提策略共需要安装VDAPF 和SVG 的容量分别为87.8 A 和21.57 A。该策略的总投资费用为505 141.11 元，实施该策略综合治理谐波和电压污染后，电能质量的综合水平为20.07%。

表2 VDAPF 和SVG 优化配置结果Table 2 Optimization allocation results of VDAPF and SVG

选取折中最优解下VDAPF 对应的谐波等效电导见附录A 表A1。

3.3 与传统配置策略的对比分析

为了验证所提策略的有效性，文中将所提策略与传统配置策略进行经济性和治理效果两方面的比较。传统配置策略分别配置CDAPF 和SVG 治理谐波和电压偏差。

1）经济性对比

为有效对比两种配置策略的经济性，令传统策略的电能质量水平与所提配置策略的治理水平相等，设置为20.07%。在此情况下，优化传统策略的投资费用目标函数。两种策略治理设备的最佳接入位置、容量以及总投资成本见附录A 表A2。对比两种策略可知，当治理效果相同时，所提策略的投资费用比传统策略减少了89 539.23 元。主要是因为VDAPF 在治理谐波的同时，其剩余容量承担了部分无功补偿工作，这在一定程度上减小了治理电压偏差对SVG 补偿容量的需求，使得SVG 配置容量减小了28.79%。可见，利用VDAPF 剩余容量参与无功补偿可有效减少系统投资费用，实现更为经济合理的配置。

2）电能质量治理效果对比

为了客观对比所提策略与传统策略的电能质量治理效果，设置传统策略的总投资成本与文中所提策略的总成本相同，即505 141.11 元。在此基础上，优化传统策略的电能质量治理水平目标函数。两种配置策略优化结果见附录A 表A3。对比可知，文中所提策略对谐波和电压偏差综合治理时，需要在节点23、32 同时安装VDAPF 和SVG，在节点8、16、20单独安装VDAPF，才能满足治理要求，此时系统的平均电能质量水平为20.07%。然而，在两种策略总投资费用相同的情况下，传统策略使系统的平均电能质量水平保持在23.56%左右，比文中所提策略的电能质量水平高3.49%。

两种策略治理前后节点的电压畸变率和电压偏差绝对值分布如图4 所示。由图4 可知，接入VDAPF 和SVG 后各节点的电压畸变率和电压偏差平均值分别为3.016%和3.257%，分别低于GB/T 14549—1993［29］规定的谐波畸变限值4.0% 和GB/T 12325—2008［30］规定的电压偏差限值7.0%。然而，根据传统策略分别接入CDAPF 和SVG 治理设备后，各节点电压畸变率和电压偏差的平均值分别为3.457%和3.906%。尽管它们均在国家规定的限值内，但存在部分节点的电能质量水平接近限值，很容易发生电压越限。可见，所提策略的电能质量治理效果优于传统策略。

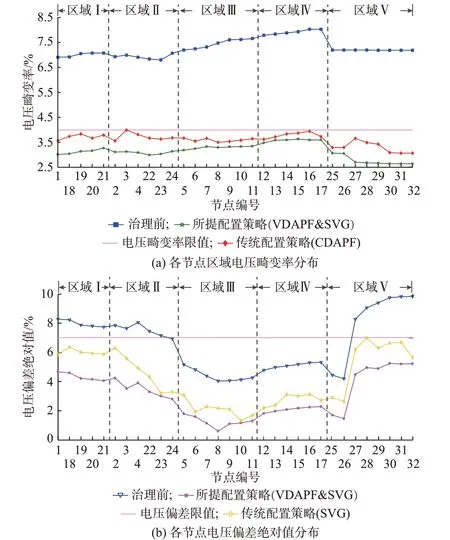
图4 治理前后各节点的电能质量分布Fig.4 Distribution of power quality before and after mitigation at each node

由上述分析可知，与传统策略相比，文中提出的VDAPF 和SVG 协同优化配置策略，既能有效减少治理设备的投资费用，又能同时提高谐波和电压的综合治理效果。

4 结语

本文提出一种面向谐波和电压综合治理的VDAPF 与SVG 协同优化配置策略，并以IEEE 33节点系统进行算例分析。主要贡献和结论如下。

1）提出的VDAPF 和SVG 协同优化配置策略中VDAPF 同时具有谐波和电压偏差治理功能，实现了全网各节点谐波与电压偏差的综合治理，提高了配电网多种电能质量治理的整体协同性，降低了设备投资成本。

2）提出的基于电压综合灵敏度的分区算法将网络划分为节点耦合程度较高的若干区域，实现了谐波和电压偏差的区域治理。同时，依据两种灵敏度指标选取区域主导治理节点作为VDAPF 和SVG 的候选接入节点，保证了候选节点的有效性。

3）建立兼顾经济性和治理效果的VDAPF 和SVG 协同优化配置模型，并采用NNC 法进行求解，获得了一系列比较完整的配置方案，为不同决策需求提供了选择。

本文仍存在的不足是配电网中同样存在三相不平衡、电压波动和闪变等电能质量问题，而本文只针对谐波和电压偏差两种电能质量问题进行分析，提出相应治理设备的协同配置策略。因此，需进一步研究考虑三相不平衡、电压波动等电能质量问题的综合治理策略。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。