基于下垂曲线截距调整的直流微电网自适应虚拟惯性控制

王 慧，赵书强，孟建辉，王 琛，田艳军

（河北省分布式储能与微网重点实验室（华北电力大学），河北省保定市 071003）

0 引言

随着新能源渗透率的提升和直流负荷占比的增加，直流电网凭借换流环节少、线路损耗低和可控性高等优点受到广泛关注［1-3］。然而，由于换流器的隔离作用，直流电网缺乏旋转动能的惯性支持［4-5］，采用广泛应用的下垂控制时，负荷突增、突减以及功率随机波动都会在不同程度上引起直流电压的快速波动［6-8］。

提高直流电网的惯性是减小直流电压波动的有效途径之一。文献［9-10］采用虚拟惯性控制方法增强直流电网的惯性，平抑了直流电压的波动，但虚拟惯量值是恒定的。实际应用时可充分利用虚拟惯量的灵活可调特性适时调整。理论上，虚拟惯性越大，直流电压在暂态情况下的变化幅度越小，对改善系统电压质量越有利，但过大的虚拟惯性会造成系统动态响应变慢，可能导致系统的不稳定。因此，亟须研究直流电网的自适应虚拟惯性控制（adaptive virtual inertia control，AVIC）方法以进一步改善系统的稳定性和动态性能。

目前，已有多种直流电网的AVIC 方法被提出［11-17］。文献［13-14］模拟直流电机的特性，通过建立虚拟惯性与电压变化率的函数关系，使虚拟惯性能根据系统的运行状态自适应调节，从而改善系统的动态性能，但由于直流电机外特性模拟和AVIC环节的引入，换流器的控制结构变得相对复杂，不利于控制算法的实际应用。文献［15］以虚拟电容控制为基础，根据电压变化率的动态变化，利用幂函数计算虚拟电容，提高了系统的动态性能，但幂函数限幅特性较差，易导致虚拟电容过大、换流器功率指令执行受阻等问题。文献［16-17］提出一种基于变下垂系数的AVIC 方法，为虚拟惯性的实现及其自适应控制提供了一条新的思路。该方法根据电压和电压变化率的动态变化，利用反正切函数计算下垂系数。在负荷突变时，既能让换流器提供很大的惯性支持，又能防止换流器输出功率越限，但反正切函数对小变量比较敏感，在过渡至新的稳态时，虚拟电容较大，暂态响应时间过长。

综上所述，现有的AVIC 方法虽然提高了直流电压的稳定性，但仍存在弊端，例如控制算法复杂、输出功率易越限、暂态响应时间过长等。因此，本文通过下垂曲线截距调整的方式实现虚拟惯性控制，并在此基础上，充分利用反正切函数和幂函数的优点，提出一种基于下垂曲线截距调整（droop curve intercept adjustment，DCIA）的直流微电网AVIC 方法。所提方法控制结构简单，可在充分利用换流器惯性支持能力的同时避免功率越限，并减少暂态响应时间。

本文首先给出直流微电网的拓扑结构、电压下垂控制方法。其次，分析基于下垂曲线截距调整的虚拟惯性控制原理，并在此基础上提出一种直流微电网AVIC 方法。然后，建立含AVIC 的四端直流微电网小信号模型，并进行稳定性分析。最后，通过硬件在环仿真验证了所提方法的有效性。

1 直流微电网的拓扑和控制

1.1 直流微电网的拓扑结构

本文所研究的直流微电网拓扑结构如图1 所示，系统由储能系统、交流电网、风电和交流负荷4 个部分组成。

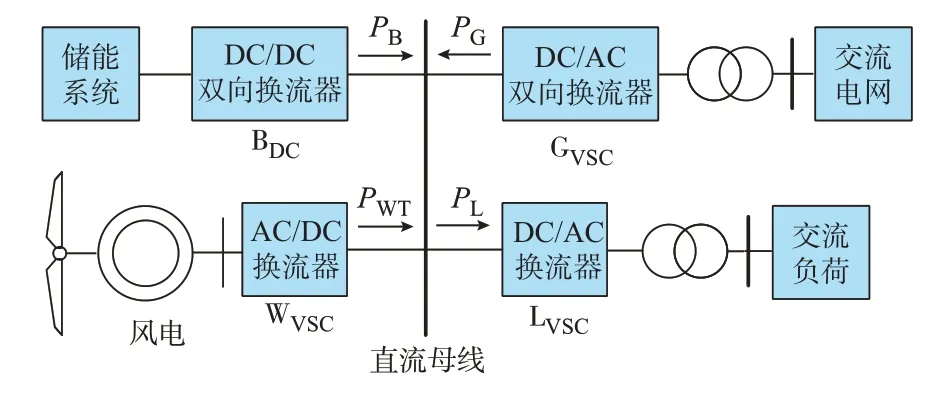
图1 四端直流微电网拓扑Fig.1 Topology of four-terminal DC microgrid

1）储能系统：采用蓄电池储能，通过双向换流器BDC并入直流微电网。BDC采用电压下垂控制。

2）交流电网：直流微电网通过双向换流器GVSC连接交流电网。GVSC采用电压下垂控制，与BDC共同协调直流母线电压。

3）风电机组：风电机组采用永磁同步发电机组，通过换流器WVSC并入直流微电网。为了尽可能地利用风能，WVSC运行于最大功率追踪状态。

4）交流负荷：交流负荷由换流器LVSC供电。LVSC采用定交流电圧控制，交流负荷的电压特性忽略不计。

1.2 电压下垂控制

由于在无通信的情况下能实现电源之间的功率分配，下垂控制在电力系统获得广泛应用。在直流微电网中，通常采用基于电压信号的控制方法。应用于某个双向换流器的有功功率-电压(PU)下垂曲线［18］如附录A 图A1 所示。该曲线可表示为：

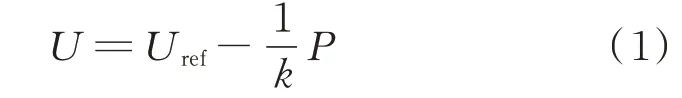
式中：P为输出功率；U为电压；Uref为下垂曲线的纵截距；1/k为下垂系数。

2 基于DCIA 的虚拟惯性控制原理

2.1 虚拟惯性的实现

调整下垂曲线的方法共有2 种，即调整下垂系数和调整下垂曲线的截距［18-19］。调整下垂系数能控制换流器快速释放或吸收功率，从而实现虚拟惯性控制。同理，调整下垂曲线的截距也能实现该功能，原理如附录A 图A2 所示。图中M0为稳态时下垂曲线的位置，a点为初始运行点，Ua和Pa分别为a点对应的电压和输出功率，Pb和Pd分别为b和d点对应的输出功率。

负荷增加至Pb时，采用下垂控制，系统运行点将由a点移动到b点，换流器输出功率增加至Pb，以重新建立功率平衡状态。在此过程中，若增大下垂曲线的纵截距，则可使下垂曲线快速平移至M1的位置。此时，系统运行点由a点移动到c点，换流器输出辅助功率，以延缓直流电压的下降速度。同理，负荷减少至Pd时，通过减小下垂曲线的纵截距，可使下垂曲线快速下移至M2的位置，系统运行点由a点移动到d点，直流电压的上升速度因此降低。值得注意的是，由于下垂曲线平移过程中下垂系数未发生变化，在容量范围内下垂曲线截距的调整量与换流器输出功率的变化量存在简单的线性关系。

由上述分析可知，通过DCIA 的方式实现虚拟惯性控制较为简单。与虚拟直流电机、虚拟电容控制相比，其简单性体现在原理上；而与下垂曲线摆动（droop curve swing，DCS）［17］相比，其简单性则主要体现在调整方向和调整量2 个方面。

1）下垂曲线的调整方向易于判断。采用DCS的方式，下垂曲线的摆动方向不仅与电压变化方向有关，还与U-Uref的正负有关。而采用DCIA 的方式，下垂曲线的平移方向仅与电压变化方向有关，只需要朝着电压变化的反方向平移即可。

2）下垂曲线的调整量与辅助功率的关系更为简单。在换流器容量范围内采用DCS 的方式，辅助功率不仅与下垂曲线摆动的角度有关，还与换流器的运行点有关；而采用DCIA 的方式，辅助功率仅与下垂曲线纵截距的调整量有关，两者的标幺值之比为k。

2.2 虚拟电容的估算

为了估算虚拟惯性的大小，需要推导虚拟电容的表达式。含虚拟惯性控制的换流器等效电路如附录A 图A3 所示。直流侧虚拟电容Cvir和两侧功率的关系为：

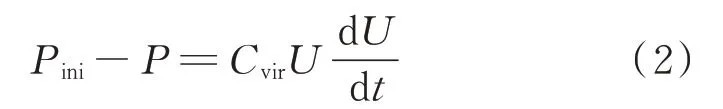
式中：Pini为不考虑辅助功率时换流器提供的功率；t为时刻。

当电压变化率(dU/dt)为正时，应减小Uref以阻止电压继续升高，反之则应增大Uref。假设下垂曲线截距随dU/dt线性变化，则Uref为：

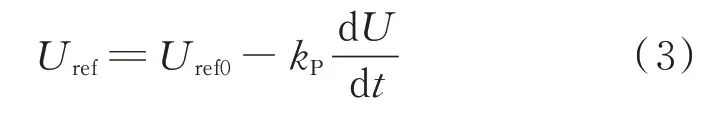
式中：Uref0为稳态时下垂曲线的纵截距；kP为下垂曲线纵截距调节参数，且kP＞0。

将式（3）代入式（1）得：

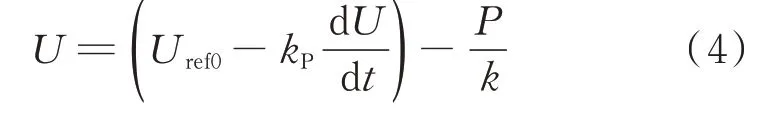
由式（4）继续推导得：

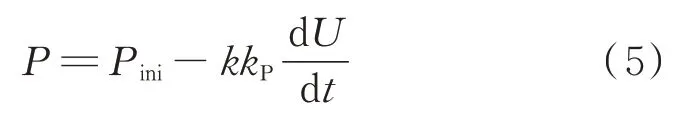
对比式（2）和式（5），消去dU/dt，得：

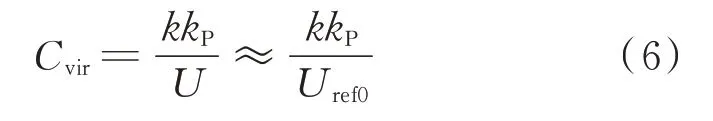
由式（6）可知，Uref随dU/dt反向线性调整的方式近似于Cvir恒定的虚拟惯性控制，并且kP越大，Cvir越大。

kP反映了下垂曲线纵截距调整量与|dU/dt|的比值大小。建立|ΔUref|关于|dU/dt|过原点的函数，并作函数曲线过原点的割线，kP在数学上则为该割线的斜率。因此，通过设计ΔUref关于dU/dt的函数，使kP根据系统的运行状态自行调整即可实现AVIC。

3 直流微电网AVIC 方法和实现

3.1 AVIC 方法

通过设计ΔUref关于dU/dt过原点的非线性函数可以实现AVIC，但此时，“自适应”是在允许的范围内灵活调整，需要满足系统的各种约束条件［20］。为了避免换流器输出功率超过限定值（以下简称超限），应对下垂曲线的纵截距加以限制。同时，函数曲线的变化趋势将直接影响各点kP的大小，进而影响系统的稳定性和动态性能。因此，应根据控制要求设计函数曲线的变化趋势。

本文利用嵌套函数计算下垂曲线纵截距的调整量，提出一种基于DCIA 的AVIC 方法，ΔUref的表达式为：

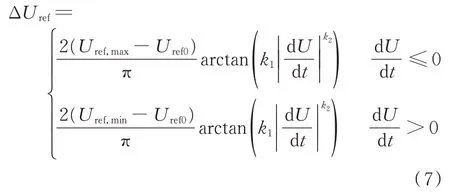
式中：Uref，max和Uref，min分别为下垂曲线纵截距的最大和最小值；k1和k2为虚拟惯性调节参数，且均大于0。

式（7）采用嵌套幂函数的反正切函数计算下垂曲线纵截距的调整量，具有诸多优势。

附录A 图A4（a）给出了k1和k2在不同取值且均经过e点的嵌套函数曲线。在接近稳态区间时（例如(0，x1]），曲线变化趋势存在明显的差异；在过e点后，所有曲线变得平缓，函数值随着变量的增大逐渐趋于限值，但不会越限。可见，嵌套函数兼具幂函数的灵活调节特性和反正切函数的限幅特性。

附录A 图A4（b）以k2=1 和k2＞1 为例，给出了2 条嵌套函数曲线的典型割线。图中kP1～kP7均为参数。假设x代表|dU/dt|，y代表|ΔUref|，则kP在一定程度上代表虚拟电容的大小。采用反正切函数时，kP5＜kP3＜kP1，其中随着|dU/dt|的减小，割线的斜率逐渐增大。如果采用k2＞1 的嵌套函数，在|dU/dt|较小时，kP2＜kP4，|dU/dt|越小，割线的斜率越小；在|dU/dt|较大时，函数值快速增加，割线的斜率较大；当|dU/dt|持续增大至e点右侧时，kP6＞kP7，割线的斜率随|dU/dt|的增大而减小。可见，采用反正切函数后，负荷突变后的暂态过程中|dU/dt|逐渐变小，虚拟电容越来越大，暂态响应时间越长。如果采用k2＞1 的嵌套函数，在|dU/dt|较小时，可降低函数对小变量的敏感度，从而减少暂态响应时间；在|dU/dt|较大时，换流器有较强的虚拟惯性支持能力，直流电压的波动得以有效抑制；在|dU/dt|很大时，虚拟电容减小，从而避免换流器输出功率越限。

综上所述，本文所提AVIC 方法充分利用了幂函数和反正切函数的优点，在改善直流微电网的稳定性和动态性能方面具有优势。

此外，为了充分利用换流器提供虚拟惯性的能力，避免换流器输出功率越限，须对不同运行点对应的Uref，max和Uref，min进行实时计算。下垂曲线纵截距的调整范围如附录A 图A5 所示。f点为初始运行点，换流器在扰动瞬间提供辅助功率，受换流器的容量限制，下垂曲线最高能平移至点Mhigh。因下垂系数恒定，由三角形1 可知，最大纵截距为：

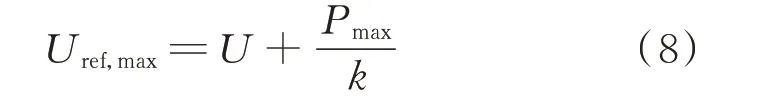
式中：Pmax为功率最大值。

同理，下垂曲线最低能平移至点Mlow。由三角形2 可知，最小纵截距为：

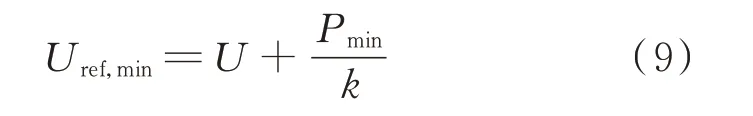
式中：Pmin为功率最小值。

3.2 控制系统的实现

在实际系统中，电压变化率的检测易受噪声及谐波的干扰。因此，本文不直接测量dU/dt，而是先对电压信号进行低通滤波，然后以高通滤波器输出的电压变化量δU代替dU/dt［21-22］。在采样周期恒定的情况下，δU与dU/dt一一对应，δU能反映系统电压的变化方向和变化速度。电压采用标幺值表示，δU远小于1。采用δU代替dU/dt，主要影响参数k1和k2的取值，而不会影响系统的稳定性与动态性能。根据式（7），ΔUref的表达式更新为：

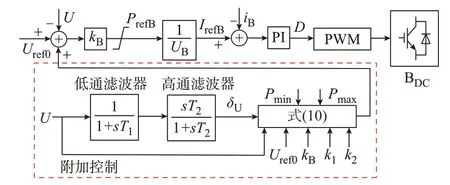
图2 BDC 控制框图Fig.2 Control block diagram of BDC

附加控制环节结构简单，本质上为δU的负反馈控制。当系统处于稳态时，δU=0，施加的AVIC 环节不起作用，不会对下垂控制的功率分配等性能造成影响。当系统受到负荷突变、新能源功率波动等扰动时，δU≠0，施加的AVIC 环节被激活，下垂曲线的纵截距向δU的反方向调整，输出功率的参考值快速变化。BDC能及时跟踪输出功率的参考值，AVIC 得以实现。

采用AVIC 的过程中，电压下降时的BDC出力更多，蓄电池释放的电量也更多，电压上升时则与之相反。总体而言，附加AVIC 后，储能系统的荷电状态变化量不会发生明显变化。与传统下垂控制一样，本文所提控制方法的实现要求储能系统的荷电状态处于可双向充放电的范围。

4 直流微电网小信号建模与参数分析

4.1 直流微电网的小信号模型

为了探究参数变化对系统稳定性的影响，需要对图1 所示的直流微电网进行小信号建模。建立的小信号模型见附录B。

4.2 参数分析

由式（10）可知，影响本文所提AVIC 方法的主要参数有Uref0、kB、k1和k2。在直流微电网中，根据系统对直流电压偏差和换流器的功率限值，Uref0和kB一般是确定的。因此，k1和k2成为AVIC 的关键参数。k1和k2的选取虽然不会导致换流器功率越限，但可能导致虚拟惯性过大或过小，从而影响系统的稳定性和动态性能。

4.2.1 参数变化对|ΔUref|的影响

附录A 图A6（a）为k1恒定时，|ΔUref|随k2和δU变化的曲线。由图可知，对于任意给定的δU值，|ΔUref|随k2的减小而增大，在k2＜1 时，|ΔUref|的增长迅速。由于k1较小，k2在2～3 之间时，随着δU的增加，|ΔUref|几乎不变。可见，k2越小换流器提供的辅助功率越大，但应避免k2＜1，否则极小的δU也可能引起输出功率的巨大变化。

附录A 图A6（b）为k2恒定时，|ΔUref|随k1和δU变化的曲线。由图可知，对于任意给定的δU值，k1增大，|ΔUref|随之增大。可见，k1越大换流器提供的辅助功率越大。

4.2.2 参数变化对系统稳定性的影响

本栏目旨在交流和推广卫生管理实践经验和学术研究成果，普及卫生管理知识，探讨卫生管理方法和技术，介绍国内外卫生管理科学新进展。

1）k1变化对系统稳定性的影响

附录A 图A7（a）为保持参数k2不变、k1从0 变化到2.5×108的特征根轨迹。系统存在s1～s4这4 个特征根，其中s1和s2为变化不大的实根，几乎不影响系统的稳定性。s3和s4为一对共轭复根，变化较为明显，为主导特征根。起初，s3和s4位于负实轴上，系统处于过阻尼状态，无振荡。随着k1的增大，s3和s4远离实轴并向虚轴方向移动，系统处于欠阻尼状态。若k1继续增大，大于1.9×108时，s3和s4位于右半平面，此时系统不稳定。可见，k1过大会导致系统不稳定。

2）k2变化对系统稳定性的影响

附录A 图A7（b）为保持参数k1不变，k2从0.30变化到2.00 的特征根轨迹。系统存在4 个特征根，其中s3和s4为主导特征根。起初，s3和s4位于右半平面，系统处于不稳定状态。随着k2的不断增大，当大于0.33 时，s3和s4进入左半平面，系统处于欠阻尼状态。若k2继续增大，s3和s4将位于负实轴上，系统处于过阻尼状态，稳定性逐渐增强。可见，k2过小会导致系统不稳定。

4.2.3 参数选取原则

根据系统对δU的控制要求、下垂曲线纵截距的限值、参数变化对|ΔUref|的影响和稳定性分析的结论给出参数的选取原则。

1）根据δU的控制要求、下垂曲线纵截距的限值，选取e点的坐标。 若要求将δU控制在[-δU，max，δU，max]，其中δU，max为δU的最大值，则电压变化量为|δU，max|时，换流器下垂曲线的纵截距应接近其极限值|ΔUref，limit|。因此，可将e点的横坐标设置为δU，max，纵坐标设置为接近|ΔUref，limit|的值。

2）k2的大小应适中，宜在区间（1，3）中选取。k2过小会导致暂态响应时间过长，甚至系统不稳定；k2过大会降低ΔUref对小变量的敏感程度，可能导致小扰动时换流器无法提供惯性支持。

3）当参数不能满足系统稳定性要求时，需减小k1或增大k2。

采用本文所提AVIC 方法时，根据给出的定量和定性相结合的参数选取原则，能降低参数选取的难度。

5 硬件在环仿真

为了验证所提方法的有效性和理论分析的正确性，搭建了如附录A 图A8 所示的硬件在环仿真平台［23］。本文所提的控制方法部署在实际数字信号处理器（digital signal processor，DSP）中，其他模型部署在RT-LAB 中，DSP 产生的PWM 信号经光电隔离模块与RT-LAB 的输入端口相连，实验波形通过录波仪测量得到。为了更直观地分析参数变化对系统稳定性和动态性能的影响，本文从录波仪中导出数据并将其绘入同一坐标系。

直流微电网的主要参数为：蓄电池额定电压为300 V，BDC的额定功率为15 kW，电感LB=0.25 mH，kB=10，T1=0.004 s，T2=0.100 s，参数GP=2，参数GI=50，GVSC的额定功率为30 kW，参数kG=10；WVSC和LVSC的额定功率分别为20 kW和30 kW；直流母线额定电压为500 V，电容C=1 000 μF；各端之间直流线路的长度为0.05 km，电阻为3×10-2Ω/km，电感为2.86×10-4H/km。

5.1 AVIC 方法的有效性验证

为了验证所提AVIC 方法的有效性，对功率随机波动、负荷突变下BDC的虚拟惯性响应进行测试。

5.1.1 功率随机波动测试

功率随机波动测试过程为：初始时刻，风电输出功率为7.2 kW，交流负荷为14.5 kW，直流电压由BDC和GVSC控制在492 V；在2 s 时，负荷功率发生-2.5～2.5 kW 的随机波动。

图3 为k2变化时功率随机波动测试结果。采用下垂控制时，由于直流微电网的惯性过小，直流电压变化剧烈，电压质量很差。另外，直流微电网的功率波动经GVSC传递至交流电网，对交流电网造成了一定影响。采用AVIC，设置k1=1 500，k2=1.2，下垂曲线纵截距根据直流电压的变化作出调整，换流器快速释放或吸收辅助功率以提供虚拟惯性支持，直流电压的波动被抑制，电压质量有所提高。采用AVIC，设置k1=1 500，k2=1，直流电压的波动被明显抑制，电压质量显著提高。同时，由于BDC平抑了大部分功率波动，交流电网的功率变得平滑。可见，在k1相等的情况下，k2越小辅助功率越大。

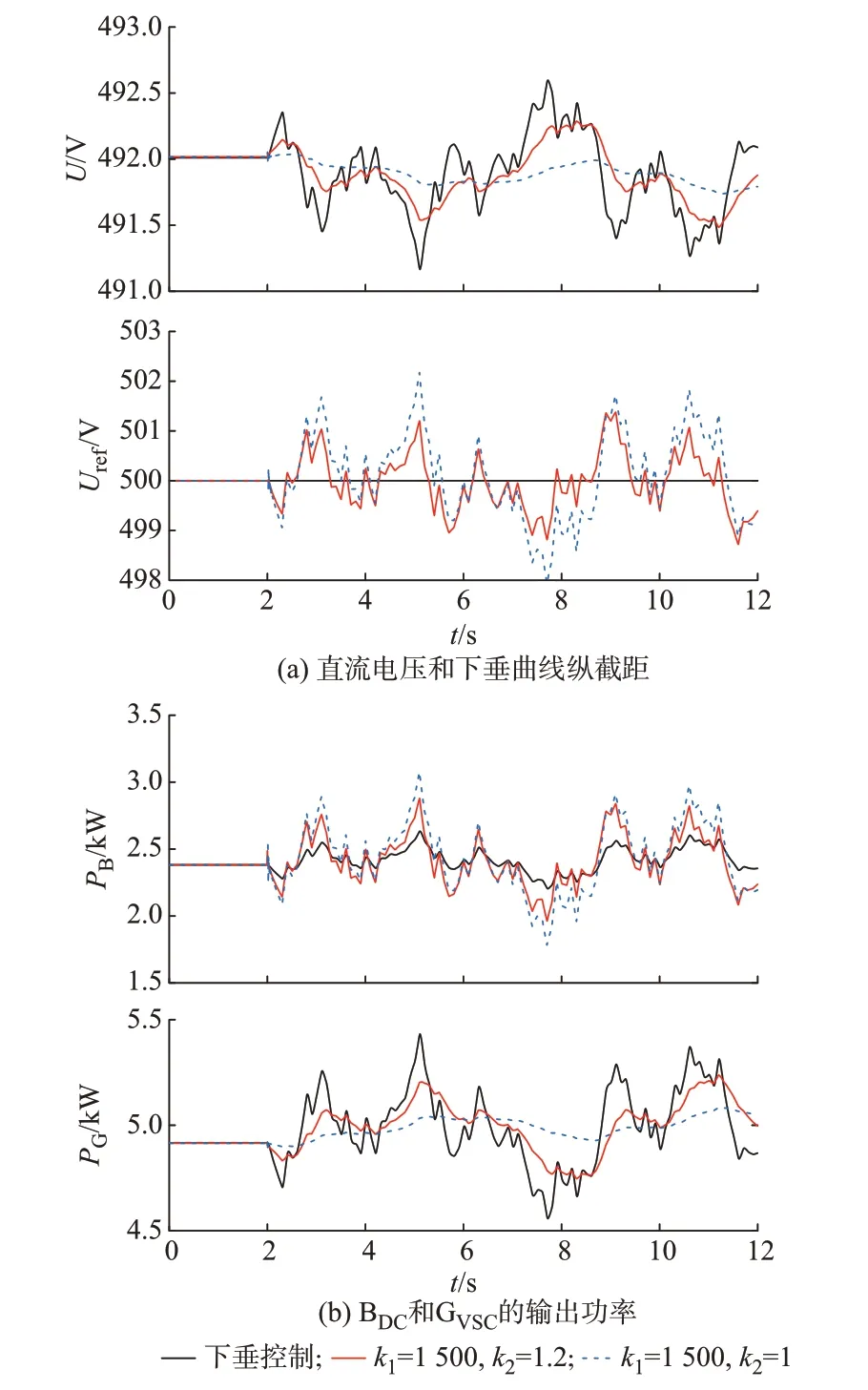
图3 k2变化时功率随机波动测试结果Fig.3 Test results of power random fluctuation when k2 changes

附录A 图A9 为k1变化时功率随机波动测试结果，其分析过程与图3 一致。采用AVIC，设置k1=5.5×106、k2=2，换流器释放或吸收的辅助功率更大、直流电压的波动相对减小，交流电网的功率变得更加平滑。可见，在k2相等的情况下，k1越大，辅助功率越大。

综上所述，采用本文所提的AVIC 方法，在功率随机波动时能为系统提供虚拟惯性支持，且k1越大或k2越小，辅助功率越大。

5.1.2 负荷突变测试

负荷突增过程为：初始时刻，风电输出功率为10 kW，交流负荷为14.5 kW，直流电压由BDC和GVSC控制在495 V；在2 s 时，负荷突增至29 kW。为了对比负荷突变后的暂态响应时间，除下垂控制外，调整k1和k2使负荷突增瞬间下垂曲线的纵截距相等。

图4 为负荷突增时暂态响应时间测试结果。采用下垂控制时，Uref始终不变，BDC不提供虚拟惯性支持，直流电压迅速跌落至479 V，暂态响应时间约为100 ms。 采用AVIC，设置k1= 5.76× 105，k2=2，负荷突增瞬间BDC立即输出辅助功率以提供惯性支持；之后，Uref快速下降，暂态响应时间较短，在5 s 时系统已基本过渡至新的稳态。采用AVIC，设置k1=2 000，k2=1，嵌套函数实际上为反正切函数，负荷突增瞬间BDC提供同样强度的惯性支持；之后，随着|dU/dt|的减小，虚拟电容逐渐增大，暂态响应时间过长，直至10 s 仍未建立新的稳态。采用AVIC，设置k1=3.39×104，k2=1.5，暂态响应时间则介于5～10 s 之间。可见，通过选取合适的参数，BDC既能在负荷突增瞬间提供较大的惯性支持，又能减小ΔUref对小电压变化率的敏感程度，从而减少暂态响应时间。

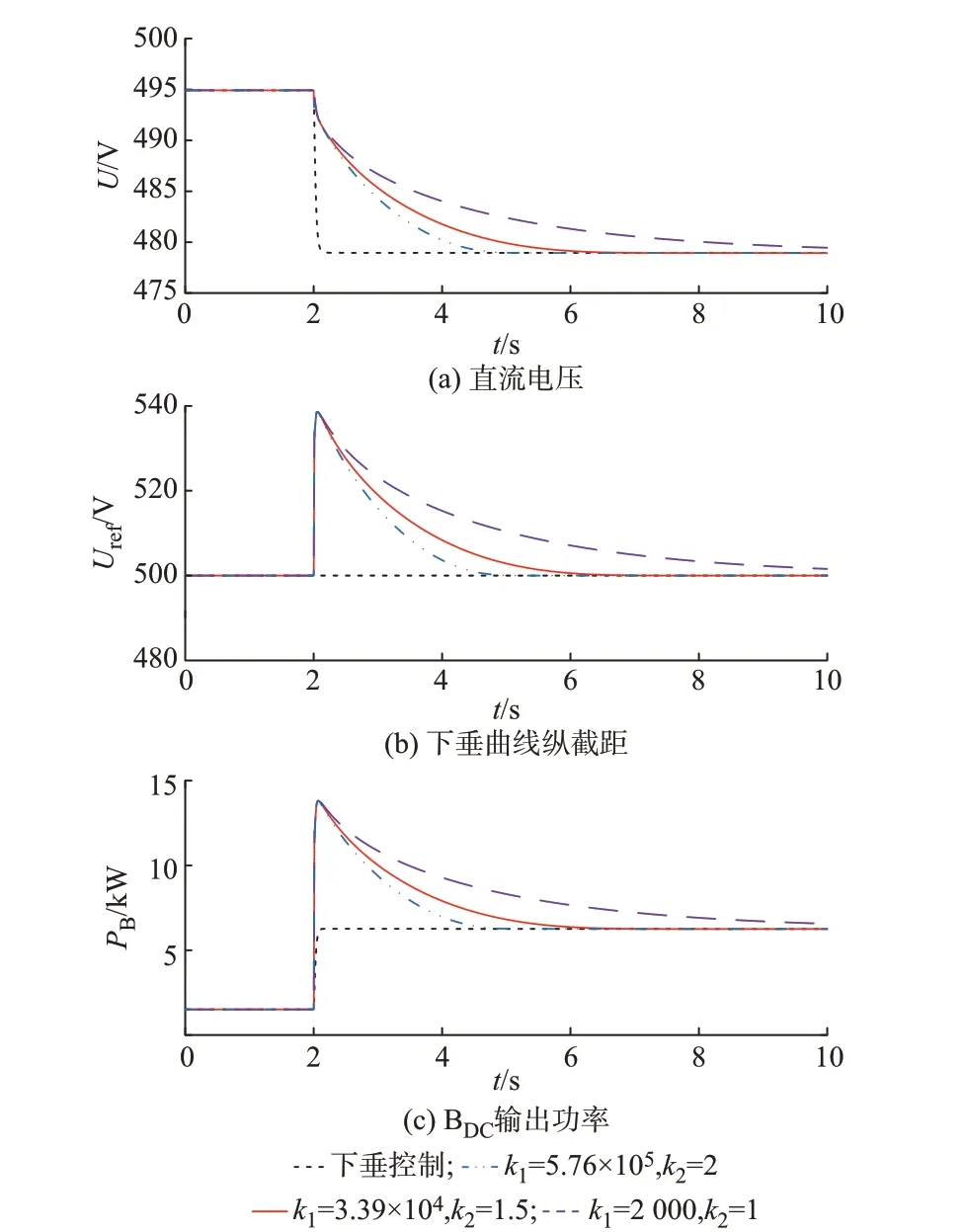
图4 负荷突增时暂态响应时间测试结果Fig.4 Test results of transient response time during sudden load increase

负荷突减过程为：初始时刻系统处于负荷突增后的稳定运行状态；在2 s 时，负荷功率恢复至14.5 kW。附录A 图A10 为负荷突减时暂态响应时间测试结果。

综上所述，通过选取合适的k1和k2，BDC既能在负荷突变瞬间提供较大的虚拟惯性，又能根据系统动态性能要求，减少暂态响应时间。

5.2 稳定性分析结论验证

通过增大k1或减小k2，可以增强系统的虚拟惯性支持能力，如附录A 图A9 和图3 所示。然而，根据4.2.2 节的稳定性分析可知，过大的k1或过小的k2会引起稳定性问题。

图5（a）为k1变化时系统稳定性测试结果。由图可知，随着k1的增大，直流电压更加平缓地趋于稳定。当k1增加至2.5×108时，直流电压出现高频振荡，并且振幅越来越大，系统的稳定性遭到破坏。

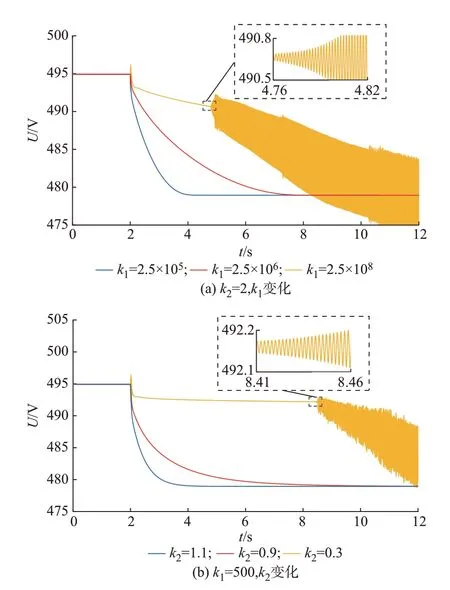
图5 k1、k2变化时系统稳定性测试结果Fig.5 Test results of system stability with change of k1 and k2

图5（b）为k2变化时系统稳定性测试结果。由图可知，随着k2的减小，直流电压更加平缓地趋于稳定。当k2减小至0.3 时，直流电压出现高频振荡，并且振幅越来越大，系统的稳定性遭到破坏。

综上所述，测试结果与稳定性分析结论一致，即过大的k1或过小的k2会导致系统失稳。

5.3 两端协调运行可行性验证

一般而言，下垂系数选取不当、负荷功率波动等易引起50 Hz 以下的低频振荡［24］。为了两端协调运行的可行性，在BDC和GVSC上施加AVIC，k1和k2的取值分别为1 500.0 和1.2。测试过程为：初始时刻，风电输出功率为10 kW，负荷在10～20 kW 之间，以频率为1 Hz 进行正弦波动；在4 s 时，负荷波动频率变为25 Hz。

附录A 图A11 为两端协调运行的测试结果。负荷波动频率为1 Hz 时，系统能稳定运行，BDC和GVSC下垂曲线的纵截距曲线基本相同，GVSC的输出功率大致为BDC的2 倍，两者输出功率的标幺值近似相等；负荷波动频率为25 Hz 时，从包络线看，系统未振荡失稳，并且两者输出功率的标幺值也近似相等。可见，两端协调运行不会轻易引发稳定性问题，在控制参数合理时，系统能稳定运行，并且在线路很短的情况下，辅助功率基本上按换流器容量分配。

6 结语

本文提出一种基于下垂曲线截距调整的直流微电网AVIC 方法，通过构建的四端直流微电网小信号模型探究主要参数对直流电压稳定性的影响规律。通过理论和仿真分析，得到如下结论。

1）鉴于下垂控制在交直流电网的广泛应用，以及下垂曲线截距调整量与输出功率变化量之间的线性关系，本文采用的虚拟惯性实现方式具有一定的优势。

2）采用AVIC 方法，并选取合适的参数能改善直流微电网的稳定性和动态性能。负荷突变瞬间，通过Uref限值实时计算和反正切函数限幅，在充分利用换流器提供虚拟惯性支持能力的同时，能避免换流器输出功率越限。同时，在负荷突变后的暂态过程中，能根据系统动态性能要求缩短暂态响应时间。

3）建立含AVIC 的四端直流微电网小信号模型，利用根轨迹法分析k1和k2变化对系统稳定性的影响，能为控制参数的选取提供一定的理论依据。

需要指出的是，通过本文所述的控制方法可以改善系统的稳定性和动态性能，但对综合考虑稳定性、动态性能和可实现性等约束的单机运行边界、优化运行，以及多机协同控制等问题还须进一步深入研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。