如何更好地理解“逆向”加法问题
□欧卓莹
“原来有一些物品,拿走一部分后,剩下另一部分,求原来有多少”,是和结构应用问题中,求总数的典型问题之一。学生在解决这类问题时,因问题的自然结构与需要解决的问题之间存在逆向关系,需要在头脑中对问题进行进一步加工,因此很多学生会出现“欲加却减”的现象。教师可以通过以下步骤帮助学生理解这一类问题。
一、阅读理解,弄清题意
1.教师出示题目(如图1),请学生自行阅读后,与同桌相互说一说知道了什么,问题是什么,即让学生把用图文结合方式呈现的问题,变成用语言表达出来。

图1
2.反馈交流,明确:已知信息是“领走了7个哨子,还剩下5个哨子”,问题是“原来有多少个哨子”。
二、层层深入,理解题意
1.想想演演:模拟场景。
(1)想一想:你想怎样演一演以上场景?
(2)借助以下两张卡片(如图2)现场模拟,感知问题场景。

图2
(3)展示学生的两种不同的演示方法。
方法1:原来的哨子-拿走7个=剩下5个
方法2:拿走7个+剩下5个=原来的哨子
教师追问:这两种演示方法有什么不同?如果把要解决的问题放在最后,怎样演示能更好地帮助我们理解题意呢?明确:方法2更合理。
(4)请学生借助卡片,用方法2再次进行现场模拟。
2.摆摆画画:图形表征。
(1)请学生用1个小圆片或者1个圆圈表示1个哨子,摆一摆或者画一画,把模拟的场景用图形表征出来。
(2)展示不同的图示,至少应包含如下两种(如图3)。
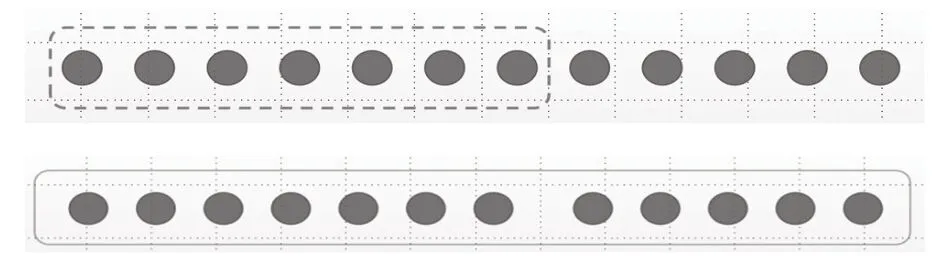
图3
(3)观察思考,评一评:哪个图能准确表示题意?图示把信息和问题都表示清楚了吗?
3.写写比比:算式表达。
(1)学生尝试列式解答。
(2)展示不同答案:12-7=5(个),7+5=12(个),7-5=2(个)。
(3)将图式进行联系、比较,确定符合加、减法意义的算式表达写法。
引导学生观察发现:不同的加、减法算式都用到了题目中的两个数7和5。
请学生指着示意图说一说:它们分别表示题目里的哪个信息或问题?
引导学生思考:哪个算式表示题目里的信息和问题更准确?
小结:已知信息是哨子总数的两个部分量,要解决的问题是哨子的总数有几个,根据加法的意义,应该用加法计算。
明确:虽然12-7=5也能表示哨子总数和两个部分量的关系,但是在列式计算时,应把要解决的问题放在最后面,因此这题用减法表示不合适。而7不是哨子的总数,所以不应该用7-5来表示。
通过以上步骤能很好地帮助学生转化“逆向”加法解决问题的思维,明白为何用加法而不用减法计算。

