GNSS-RTK 技术下悬索桥动态变形监测方法研究

李 志，张雪芳

（1.长江科学院，湖北 武汉 430010；2.中国建筑科学研究院有限公司，北京 100013）

0 引言

桥梁在服役过程中，由于材料老化、腐蚀等问题导致结构产生内部损伤，同时在风荷载、交通荷载及地震荷载等因素影响下，这些损伤会不断积累加剧，使桥梁结构性能在服役过程中不断退化。因此，为保障桥梁的安全与稳定，亟需采用合理有效的技术手段对在役桥梁进行实时动态监测［1-4］，准确反映桥梁在复杂动态荷载作用下振动响应，以预防和避免桥梁事故的发生。

1 基于 GNSS-RTK 的桥梁动态变形监测原理

目前 GNSS-RTK 技术已在大型土木工程结构健康监测领域得到了广泛应用［5-7］。基于 GNSS-RTK 技术的桥梁动态变形监测可以实现桥梁结构的全天候实时监测，获取结构动态响应信息，降低监测成本并大大提高结构监测效率，从而为桥梁结构的安全评估提供更有利的数据支撑［8-10］。尽管在监测过程中，RTK 技术可以有效消除或抑制相对论效应误差、卫星时钟误差、接收机时钟、大气折射误差及卫星星历误差的影响，但对多路径误差的抑制作用不大。因此，本文在 GNSSRTK 监测技术基础上，提出 WPD-EEMD 联合滤波方法，并结合 MAF 方法对监测数据进行处理，以削弱多路径误差以及其他随机误差对监测结果的影响。

1.1 WPD 降噪方法

小波包阈值降噪方法是将原始信号进行小波包分解并计算其阈值，而后获取得到小波包分解后的各层小波包系数。将各层小波包系数的模值与计算出来的阈值进行比较，舍弃低于阈值的小波包系数，将其余高于阈值的小波包系数进行重构，最终得到滤除信号。小波降噪具体步骤如下。

1）选择一个小波基并确定分解层次，然后对原始信号进行小波包分解，分解算法如式（1）所示。

2）计算最佳小波包分解树，求解最佳小波包基。

3）计算阈值，比较计算所得阈值与各层小波包系数，对最佳正交小波包基对应的每一层小波包系数进行阈值量化处理。

（4）对处理后的小波包系数采用小波包重构算法得到重构信号小波包，重构算法如式（2）所示。

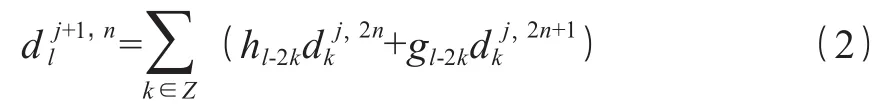
式中：hl-2k和gl-2k为一对正交共轭滤波器系数。

1.2 EEMD 算法

EEMD 是针对经验模态分解（EMD）方法中存在的不足提出的一种噪声辅助数据分析方法，很好地解决了 EMD 存在的模态混叠问题。它的基本原理是将白噪声加入待分解的信号之中，使得白噪声的分布遍布整个信号的时频空间，基于白噪声频谱均匀分布这一特性，不同时间尺度的信号会自适应地分布到匹配的参考尺度上，经过若干次平均后，噪声将相互抵消，集成均值的结果就可作为最终结果。其分解步骤如下。

1）在原始信号x（t）中加入一组均值为零、方差相等的白噪声序列ω（t），生成一个新的信号X（t），如式（3）所示。

2）通过 3 次样条插值分别形成原始数据的上包络线和下包络线，计算上下包络线的平均值，然后用原始数据减去平均值可以得到一个新的数据系列。

3）在执行完上述步骤后，若数据序列仍存在局部最大值和最小值，表明该数据序列不是一个本征模态函数（IMF），需要对其继续执行上述操作，直至不出现局部极值为止，如式（4）所示。

4）最终数据被分解成为一系列 IMF 和一个残余信号r（t），如式（5）所示。

1.3 WPD-EEMD 算法

本文提出的 WPD-EEMD 算法流程如下。

1）将含有噪声的监测信号经过前期预处理之后得到信号；

2）将信号进行小波包分解，获得各层小波包系数，计算阈值；

3）选取用于重构小波包信号的小波包系数，进行第一次信号重构，得到滤除掉部分高频噪声和部分低频噪声的信号；

4）将 WPD 降噪信号经 EEMD 进行分解，得到其从高阶到低阶排列的本征模态函数IMF；

5）计算各个IMF与原信号的相关系数ρ，将相关系数仅作为选取主要IMF成分的一个指标，相关系数计算公式如式（6）所示。

式中：cov（IMFi（t），x（t））为第i阶IMF分量与原始信号x（t）的协方差，σIMFi（t），σx（t）分别是第i阶IMF分量与原始信号x（t）的标准差。当ρ＞0.8 时，可认为X和Y具有强相关性；当ρ＜0.3 时，可认为X和Y具有弱相关性；当0.3＜ρ＜0.8 时具有中度相关性。

6）进一步地，结合相关系数和各个IMF的瞬时频率，选取主要IMF成分用于重构信号的，最后滤除高低频噪声。

2 实例应用

2.1 监测试验

以天津富民桥为监测对象，全桥由三跨混凝土连续梁、单塔空间索面自锚式悬索桥和单悬臂混凝土框架结构组成。全桥总长 340.3 m，主跨 157.1 m，辅跨 86.4 m，如图 1 所示。

图1 天津富民桥

在进行现场监测之前，建立了桥梁的三维有限元模型，分析了结构前 6 阶竖向振型，固有频率分别为 0.570 5，0.710 4，1.129 0，1.400 9，1.788 0，2.101 5 Hz，如图 2 所示。

图2 富民桥有限元模态分析

根据奈奎斯特采样定理，当采样频率大于信号中最高频率的 2 倍时，采样之后的信号能完整地保留原始信号中的信息。鉴于此，现场试验设置 GNSS 接收机的采样频率为 10 Hz，先进行 GNSS 稳定试验以分析背景噪声，分析结果可知，系统低频噪声主要在 0.06 Hz 以下，高频噪声近似服从高斯白噪声分布。由有限元模态分析可知，试验桥梁固有频率＞ 0.06 Hz，故可以通过常规滤波方法去除系统低频噪声，以提高系统监测精度。本文提出的 WPD-EEMD 联合降噪方法旨在抑制高频噪声，进一步提高 GNSS-RTK 技术的监测精度。

现场试验持续进行 24 h，以监测结构在正常运营状态下的振动响应。由图 3 分析可知，桥梁变形极大值出现在主跨的 1/4 处、1/2 处及 3/4 处，因此在该处布置 GNSS 接收机可以有效地捕捉结构的振动特性。图 3 为 GNSS 布置平面图。

图3 GNSS 布置示意图（单位：cm）

2.2 监测数据分析

选取 C2 点处的监测数据进行分析，其余点分析类似。图 4 为原始位移信号时程曲线，位移幅值介于 -3.7～3.2 cm。图 5 显示了经过 WPD 降噪后的位移信号时程曲线，位移幅值介于-3.2 cm 到 2.7 cm 之间。对比图 4 和图 5 可知，由于 WPD 降噪方法消弱了高频噪声的影响，WPD 降噪信号幅值有所下降，但降噪信号中依然存在部分低频噪声和随机噪声。

图4 原始观测信号

图5 WPD 降噪信号

采用 EEMD 对 WPD 降噪信号进行分解，得到其各阶模态分量（IMF）以及对应的功率谱密度函数图，如图 6 所示。通过考虑IMF与 WPD 降噪信号的相关系数可知，最后四阶为虚假分量。由图 6 中IMF的功率谱密度函数可知，固有频率主要存在于IMF2～IMF5 中，因此通过这些IMF分量重构信号，最终得到 WPDEEMD 降噪信号，如图 7 所示。由图 7 可知，WPDEEMD 降噪信号幅值介于-3.1～2.1 cm，WPD-EEMD 降噪处理有效滤除了位移信号中低频噪声和高频噪声，保留了原始位移信号中的有用信息成分。进一步采用 MAF 方法对监测过程中出现的随机振动噪声予以消弱，如图 8 所示。

图6 WPD 降噪信号 EEMD 分解

图7 WPD-EEMD 降噪信号

图8 MAF 滤波

通过 Hilbert 变换对分析原始信号、WPD 降噪信号、EEMD 降噪信号、WPD-EEMD+MAF 降噪信号进行时频分析，如图 9 所示。对比图 9（a）与 9（b）可知，原始信号经过 WPD 降噪后，高频噪声得到了有效的抑制，然而低频噪声降噪效果并不明显。对比图 9（a）与图 9（c）可知，原始信号经过 EEMD 降噪后，低频噪声与部分高频噪声得到了有效的抑制，降噪效果要优于 WPD 降噪。对比图 9（b）～9（d），可以看出 WPDEEMD+MAF 联合降噪方法抑制了信号的高频噪声和低频噪声，降噪效果明显要优于 WPD 及 EEMD 降噪方法。

图9 Hilbert 能量谱

3 结语

本文采用 GNSS-RTK 技术对环境激励下天津富民桥进行监测试验，研究了 GNSS 背景噪声对监测精度的影响，提出了 WPDEEMD+MAF 的监测数据处理方法，得出以下结论：由 GNSS 稳定试验结果分析可知，监测误差主要来源于高能量的低频噪声和低能量的高频噪声，其中低频噪声主要在 0.06 Hz 以下，高频噪声近似服从高斯白噪声分布；经过 Hilbert 谱分析可以看出，本文提出的 WPD-EEMD+MAF 联合滤波方法的降噪效果优于单独采用 WPD 或者 EEMD 的降噪方法，能够有效抑制 GNSS-RTK 监测数据中的多路径误差以及随机振动误差，显著提高 GNSS-RTK 的监测精度，成功识别到富民桥的动态位移信息，同时证明 GNSS-RTK 技术可有效应用于桥梁动态变形监测中。