基于工作过程的圆柱凸轮参数化造型与数控加工

陶维利

(武汉船舶职业技术学院，湖北武汉 430050)

凸轮机构由于结构简单紧凑，能使从动件实现任意的预期运动，广泛应用于机床、纺织机械、印刷机械、包装机械、食品机械、各种轻工机械和机电一体化等自动和半自动设备中。圆柱凸轮是一个在圆柱面上开有曲线凹槽或在圆柱端面上作出曲线轮廓的构件。传统的凸轮机构设计方法一般采用作图法和解析法，它们都是基于二维的设计方法，主要用于平面凸轮的设计，现在无论是平面凸轮还是空间凸轮，一般都用计算机软件来设计，如UG NX、Pro/E、Solidworks等CAD/CAM/CAE软件，本文利用UG NX为平台，介绍圆柱凸轮参数化造型的一种新方法--基于凸轮工作过程的造型方法，即模拟凸轮的实际工作过程来造型，提高了造型精度，并且利用UG NX的CAM模块对该圆柱凸轮进行数控加工程序设计。

1 圆柱凸轮的参数化造型

凸轮从动件的运动规律有多项式运动规律(如匀速运动、等加等减速运动和高阶多项式运动规律)、三角函数基本运动规律(如余弦加速度运动和正弦加速度运动规律)以及组合运动规律，本文以推程为等加等减速运动回程为匀速直线运动的圆柱凸轮为例来介绍其参数化造型方法和过程，该圆柱凸轮的基本参数为：从动件行程h=50mm，凸轮基圆半径r=30mm，槽宽b=24mm，槽深h1=18mm，推程为等加等减速运动，推程角a1=120°，远休止角a2=90°，回程为匀速直线运动，回程角a3=80°，近休止角a4=70°。

1.1 推导UG表达式

根据凸轮的运动规律，我们不难写出凸轮在各个阶段的转角φ-行程h方程[1]：

远休止期：s=h，φ∈[a1，a1+a2]

近休止期：s=0, φ∈[a1+a2+a3，a1+a2+a3+a4]

转角-行程曲线如图1所示。

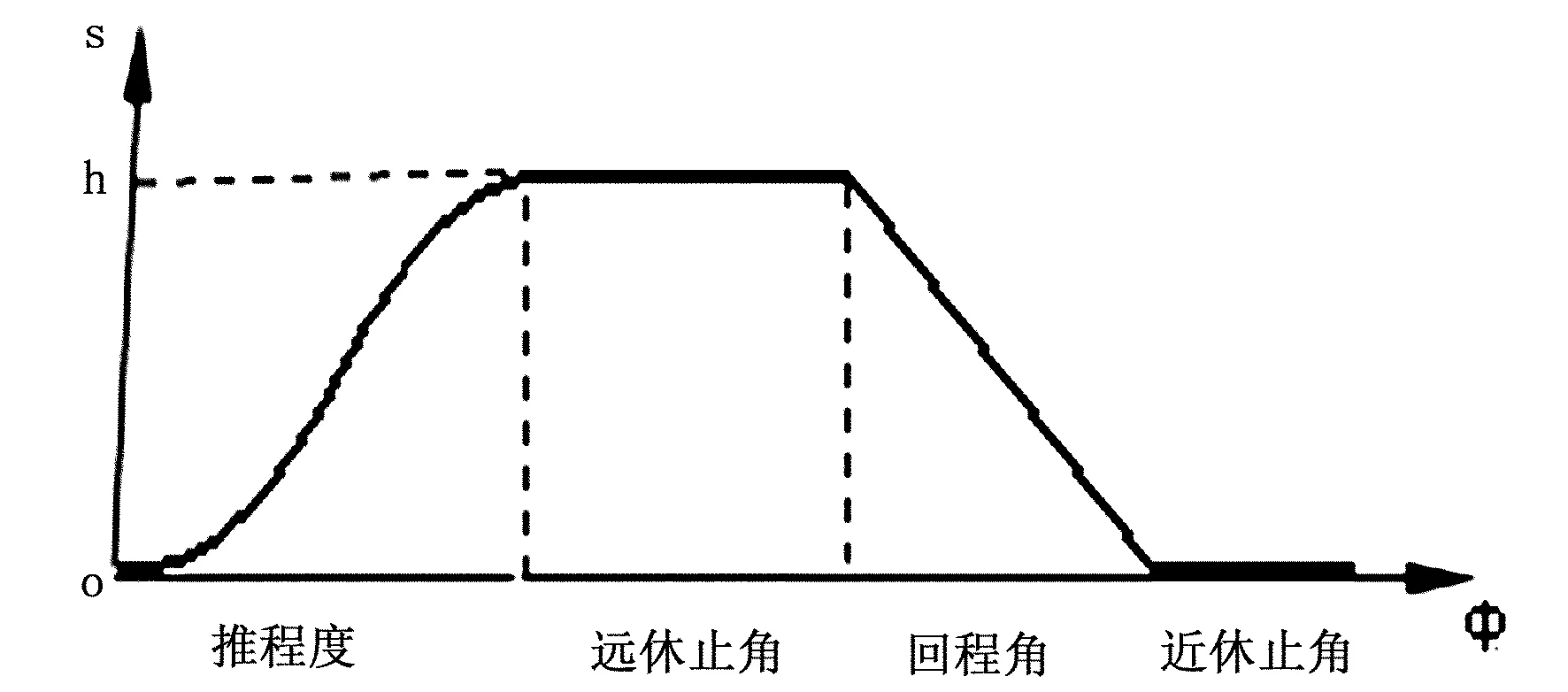
图1 转角-行程曲线

圆柱凸轮理论轮廓的参数方程为：

x=rcos φ

y=rsin φ

z=s

式中：r为基圆半径，s为从动件行程，φ为凸轮转角，因在UG中不便输入，在下文的UG表达式中我们用a来代替φ。另外，圆柱凸轮一般用四轴数控机床加工，为便于加工操作，在建模时一般将圆柱体水平放置，使圆柱体的轴线为X轴或Y轴，这取决于机床的第四轴是A轴还是B轴，本文假设第四轴为A轴，则圆柱体的轴线为X轴。

上述方程须转换成UG能够识别的表达式[2]：

t=1

a=360*t

a1=120

a2=90

a3=80

a4=70

r=30

h=50

s1=2*h*(a/a1)^2

s2=h-2*h*(1-a/a1)^2

s3=h

s4=(a1+a2+a3-a)*h/a3

s5=0

xt=if(a

yt= r*cos(a)

zt= r*sin(a)

其中：t-UG默认自变量，a-凸轮转角，a1-推程角，a2-远休止角，a3-回程角，a4-近休止角，r-基圆半径，h-行程，s1-推程前半程行程，s2-推程后半程行程，s3-远休止期行程，s4-回程行程，s5-近休止期行程，xt、yt、zt-凸轮理论轮廓线上点的坐标。当凸轮的基本参数发生改变时，只需改变相关变量的数值即可，跟此表达式相关的二维和三维模型UG软件会作相应的变更。更进一步，我们甚至可以将圆柱凸轮常见的一些运动规律全部集成到一个表达式文件中，实现圆柱凸轮的完全参数化设计。

建立上述表达式后，再利用“规律曲线”指令即可生成凸轮的理论轮廓线，如图2所示。

图2 凸轮的理论轮廓线

1.2 圆柱凸轮三维造型

圆柱凸轮三维造型的主要工作就是凸轮槽的造型，利用规律曲线生成凸轮的理论轮廓线后，有多种方法创建凸轮槽，如片体加厚法是利用轮廓线生成槽底曲面，再通过加厚片体来得到凸轮槽实体，然后再将此实体与凸轮圆柱体作布尔差运算；再如扫掠法是将凸轮槽截面线沿理论轮廓线扫掠得到的实体与凸轮圆柱体作布尔差运算来创建凸轮槽[3]。这些方法如果指令参数(即约束条件)设置不当，很容易产生较大的造型误差，如槽侧面与底面的垂直问题、槽的等宽问题等，造型完后可能还需要通过运动分析来判断造型的合格性。本文介绍一种基于工作的方法，其基本思路是用与从动件相同直径的刀具沿理论轮廓曲线运动仿真加工得到的实体作为凸轮的三维实体模型，由于建模过程与凸轮的实际工作过程高度一致，所见即所得，极大地提高了建模精度。得到凸轮三维模型后再在UG的CAM模块里进行粗、精加工的设置，生成NC程序。

生成理论轮廓曲线后，以凸轮的基圆半径为半径创建一个圆柱体，如图3所示，然后进入加工模块，选择mill_multi-axis(多轴加工)，选择可变轴轮廓铣，加工方法设为精加工，刀具直径设为从动件直径，部件设为刚才创建的基圆圆柱体，毛坯为X向的包容圆柱体，半径偏置为凸轮槽的深度，驱动方法为“曲线/点”，投影矢量设为刀轴，刀轴设为远离直线，直线设为圆柱体的轴线，这样，仿真加工过程就和凸轮的实际工作过程一样了，生成刀轨并仿真加工，然后保存，如图4所示，此即为我们所要的凸轮三维模型，然后到UG的逆向工程模块里将它转为实体，因为这个体其实是一个小平面体，如果不转为实体，会给后续的工作带来不便。

图3 理论轮廓线和基圆圆柱体

图4 圆柱凸轮三维模型

2 数控加工

圆柱凸轮的数控加工一般分为粗加工和精加工两步，也有在其中加个半精加工的，驱动方法可用“曲面”或“曲线/点”驱动，前者既可用于粗加工也可用于半精加工和精加工，后者主要用于精加工，并且要求刀具直径与从动件的直径相同，事实上，本文前面就是用此方法来得到凸轮模型的，但在实践中往往不易找到刚好合适的刀具，当然如果想用直径小于槽宽的刀具采用“曲线/点”的驱动方法来精加工槽的两侧面，那就需要根据理论轮廓曲线、刀具直径和槽宽推导或派生出槽两侧壁的精加工驱动曲线。

再次进入加工模块，先进行粗加工，选择可变轴轮廓铣，加工方法设为粗加工，用刚才得到的实体模型作为部件，毛坯使用包容圆柱体，刀具选用直径小于槽宽的铣刀(如Φ20)，驱动方法选择“曲面”，选择槽底面为驱动面，投影矢量设为刀轴，刀轴设为远离直线，直线设为圆柱体的轴线，加工余量可接受默认值或自行设定。

精加工的设置与粗加工类似，还是选择可变轴轮廓铣，加工方法设为精加工，刀具尺寸可再小一点(如Φ10等)，驱动方法选择“曲面”，当然，如果刚好有直径等于槽宽的刀具或是大批量生产，驱动方法设为“曲线/点”效果更好，因为大批量生产可定制刀具。精加工如果使用“曲线/点”驱动，就和上文建模用的方法一样了，不再赘述。

最后，选择合适的后处理器如MILL_4_AXIS处理上述工序，生成NC程序。

3 结 语

本文介绍了圆柱凸轮基于工作过程的造型方法，优点是造型过程与工作过程一致，造型精度高，不足之处在于需要将小平面体转为实体，如果UG的更高版本能将小平面体直接转为实体，此问题就可圆满解决。至于参数化造型，本文的重点不是圆柱凸轮库的建模，所以只例举了一二种运动规律的参数化建模方法。圆柱凸轮的数控加工，如果条件满足，“曲线/点”驱动方式加工精度更高，因为此加工方式与凸轮的工作过程是一致的。