基于三目视觉的圆柱尾迹层析PIV测量
段双成,杨苗,封明军,王芳婷,周骛,蔡小舒
(1 上海理工大学能源与动力工程学院,上海 200093;2 上海市动力工程多相流动与传热重点实验室,上海 200093)
粒子图像测速(PIV)是一种现代流场测量技术,不同于皮托管测速、热线测速等传统方法,PIV技术既摆脱了单点测速的限制,又实现了快速、准确、无干扰地对流场截面结构的测量,在化工、机械和能源等领域中都存在着广泛的应用,如天然气流量特性分析[1]、搅拌槽混合槽内的流动结构测量[2]、喷砂桶内部磨损模型[3]和搅拌釜内桨型设计[4]。然而二维PIV技术在研究复杂流动中的涡流及湍流方面具有一定的局限性,如换热器内翅片间流动、燃气轮机叶栅间流动等,其流道空间小,流动复杂,很难通过某一平面的二维结构反映出来。层析粒子图像技术(Tomographic-PIV)是在PIV技术上发展起来的一种三维流场测量技术,它采用一定厚度的激光体光源代替激光片光源,真正实现了3D-3C,即三维空间三个速度分量的速度场测量。
层析PIV是一种光学非定常流场测量技术,由于其具有大视场、高精度的三维测量能力,在提出之后便受到了国内外的广泛关注。Scarano[5]在2013年对层析PIV的研究进展进行了很详细的综述。层析PIV 的概念最早由2004 年由韩国的Kim 等[6]提出,并使用该技术对鼻腔内的几个平面内鼻窦气流组织进行了测量,虽然得到的结果是三维速度分布,但实际上与目前的层析PIV 并不一致;2005年,荷兰的Esinga 等[7]在两种圆形气缸中,应用层析PIV 技术对其中的湍流流动进行了测量;在第6届国际PIV 研讨会上,Esinga 等[8]正式提出了层析PIV技术,对其工作原理和成像算法的细节进行了详细的阐述,从迭代次数、相机数量以及示踪粒子密度等方面对重构精度进行了分析,并对采用了四相机系统对环状涡流模拟场进行了测量,测量误差仅为0.1 像素,表明该技术完全能够满足精度要求,并能够提供远远大于二维测量的信息量。
Esinga 等[9]在其应用于湍流边界层的实验测量方面做了一系列的研究,并对伪影粒子进行了研究;英国剑桥大学在早期提出了一种快速三维重建的方法[10],这对校正图像在空间中的映射关系至关重要,并对多种层析重建方法做出了贡献。Worth等[11]还通过数值计算评估了各向同性湍流中层析PIV 的精度;Hain 等[12]对通过圆柱体顶部的流动拓扑及有限圆柱顶部边界层和尾迹结构之间的相互作用进行了研究;Thomas等[13]对喷气机的横流射流进行了测量研究;Ortizs-Dueñas 等[14]通过层析PIV 研究了液滴在液-液平面上的聚结现象以及单个液滴之间的聚合过程,首次实现了多相流的测量;Silva等[15]对一个典型的湍流边界层层析PIV实验中的几个关键实验参数进行了分析,结果表明相机的位置、示踪粒子的数量及体素的离散程度等因素均对实验的准确性有显著影响;Violato等[16]采用时间解析层析PIV算法对从圆形出口和V形出口处的射流转捩过程进行了研究,得到了高速和低速流动区与激波边界层相互作用的拓扑结构。
上述研究表明了层析PIV的发展过程由最初的致力于层析重构算法,到逐步集中在对湍流现象上的研究,也正是由于其能够测量湍流中相干结构的三维瞬时状态,使得其应用越来越广。
国内对于层析PIV 技术的研究起步相对较晚,研究内容主要集中在低速水流、风洞中。天津大学姜楠等[17]应用改进的层析TRPIV算法,对水槽中的平板湍流边界层的三维速度场进行了测量;北京航空航天大学高琪等[18]通过自主研发的层析PIV 技术,实现了对低速合成射流的三维测量,观察到了三维涡环结构的时空演化过程;中国航空工业动力研究院许相辉等[19]对圆柱三维尾流场进行了测量,成功观测到了圆柱体后方产生的三维卡门涡流场;西南科技大学张小航等[20]采用了数值模拟的方法,通过层析PIV技术的原理及方法,以真实风洞中的测量参数为基础,对由数值计算得到的模拟流场进行了重建研究,验证了方法的准确性。这些成果极大促进了国内学者对于层析PIV的研究兴趣,促进了技术的发展。同时也显示出了层析PIV对三维涡环结构具有很好的捕捉能力,能确保实现复杂流动中涡环时空演变的定量实验研究。
因此本文基于层析PIV技术,结合3台CCD相机等硬件设施搭建了一套层析PIV测量系统,采用三维相机标定、重构算法,对水槽内圆柱绕流尾迹流场进行测量研究,完成了低速条件下的实验验证,为复杂的狭小空间流动测量奠定了基础。
1 层析PIV基本原理
层析PIV 的原理与计算机断层摄影(CT)类似,后者通过X射线面对物体进行扫描,通过计算X射线的衰减量来重建物体的某横断面结构;但流场不同于静止的物体,需要通过高速相机或具有PIV模式的相机“冻结”某一时刻下的流场,并用激光代替X射线,采用多台相机在多角度拍摄以代替X射线面的扫描,而相机采集到的图像像素值便是多粒子散射光强叠加形成的,通过反演计算便能得到粒子的空间位置,完成三维粒子光强场的重建。其测量原理示意图如图1所示,通过激光器产生激光束并通过透镜系统扩束产生具有一定厚度的体光源,照亮示踪粒子;布置至少3台CCD相机从不同角度对示踪粒子的散射光信息进行采集,并通过信号发生器使CCD相机在极小的时间间隔下拍摄两次;然后采用层析重构算法对三维粒子场信息进行重建,再利用三维互相关技术得到粒子在该时间间隔下的位移,从而实现对三维速度场的重建。
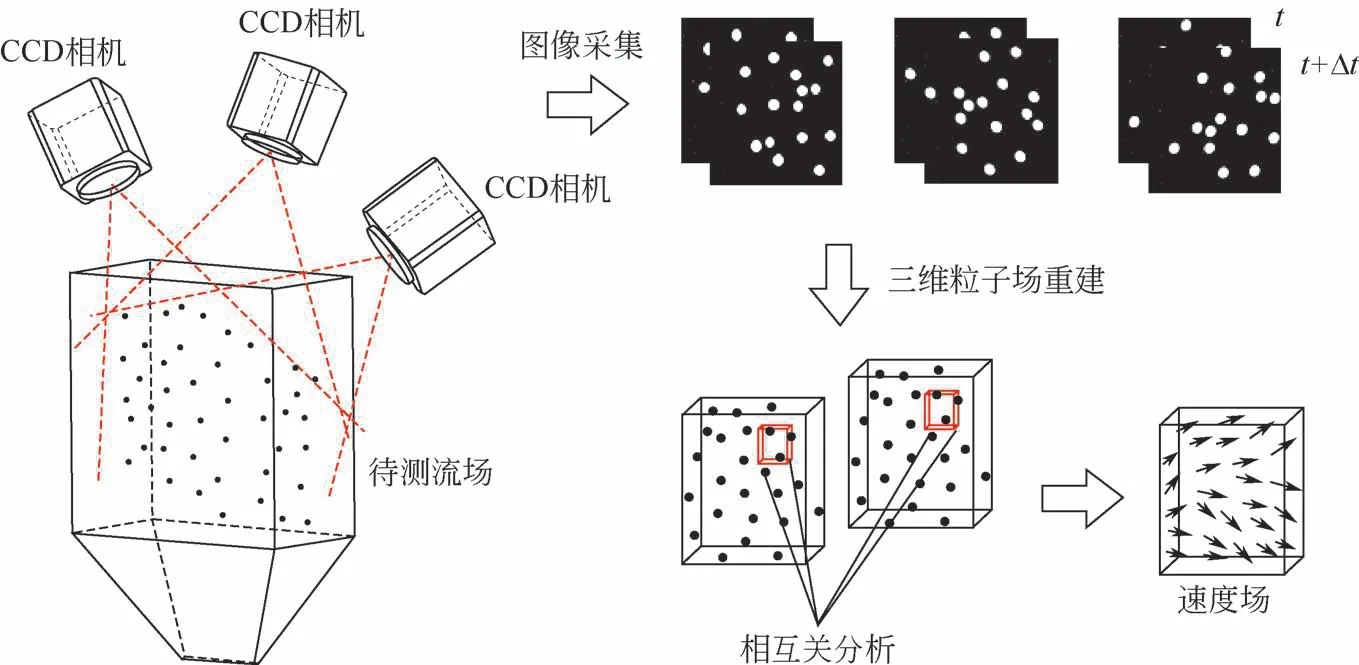
图1 三目PIV测量原理
1.1 三维标定
相机的标定实际上就是4 个坐标系的转换过程,其中包括世界坐标系、相机坐标系、图像坐标系和图像像素坐标系,其目的就是确定图像像素坐标系与世界坐标系的对应关系,以便在对采集到的图像进行处理时对物体实际坐标进行推导。图2为4种坐标系间的相互关系,其中O-XYZ为世界坐标系,o"-uv为图像像素坐标系,o'-u'v'为图像坐标系,Oc-XcYcZc为相机坐标系。由世界坐标系下某点P坐标(x,y,z)到图像像素坐标系下坐标(u,v)的转换关系如式(1)所示。
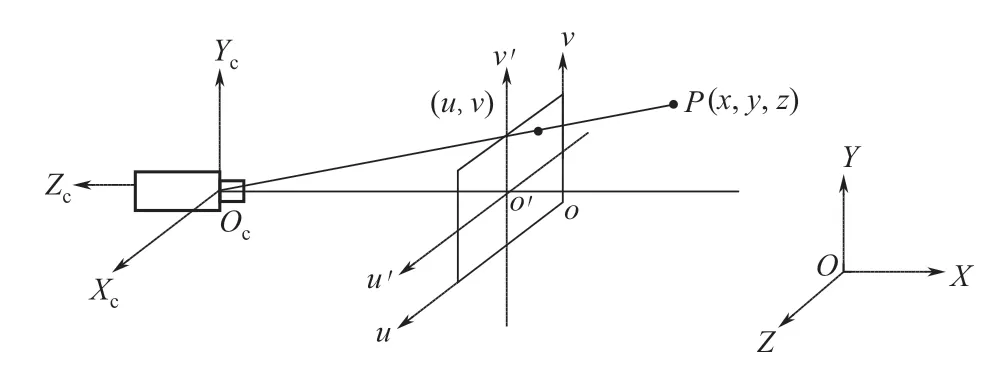
图2 坐标系概况
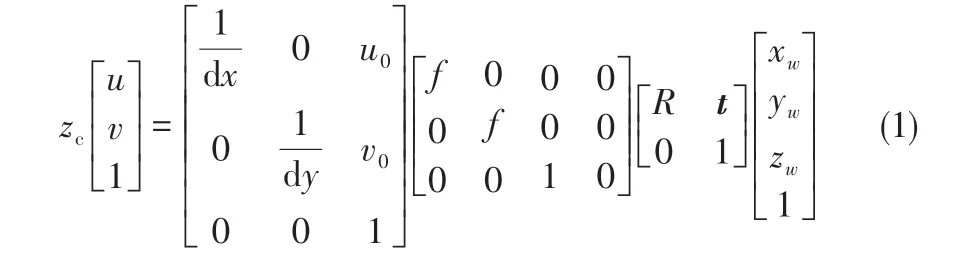
式中,R表示世界坐标系到相机坐标系的旋转矩阵;t表示平移向量;f为相机焦距;dx和dy为图像像素的物理尺寸(u0,v0)为图像中心的像素坐标。相机坐标系Oc-XcYcZc可以看成由世界坐标系O-XYZ经过旋转与平移得到。
相机坐标系到图像物理坐标系的转换则通过透镜成像的相似三角形比例关系进行计算;图像物理坐标系则以图像的中心为原点。
相机标定一般采用已知尺寸的圆点标定板或棋盘格,在不同位置和角度下进行成像,处理获得上述参数,多相机标定则是对多台相机同时获得相应的标定参数。
1.2 三维重构
单台CCD 相机只能得到二维图像强度分布,三维空间的光强分布需要通过重构获得。首先需要将被测流场的三维区域进行离散化,得到若干数量的体素;根据粒子成像理论可以得到,单个像素的强度值是基于空间视线内多个粒子散射强度的线性积分,所以可以得到式(2)。
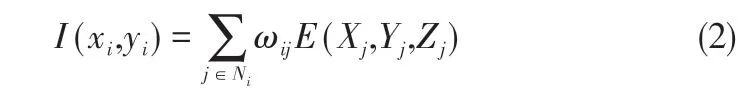
式中,I(xi,yi)为图像像素强度;E(Xj,Yj,Zj)为体素散射光强;Ni为光线所截取的或在光线邻域内的体素数量;i表示相机的第i个像素;ω(i,j)为权重系数矩阵,代表了体素对像素强度的贡献率。
不难看出,若要得到三维光强分布,首先要得到权重系数ω(i,j)。图3为重构的数学模型,描述了在一个层析平面上的重构过程。权重系数矩阵ω(i,j)由体素相对于像素的尺寸以及体素中心与光线的距离决定,且有0≤ω(i,j)≤1。
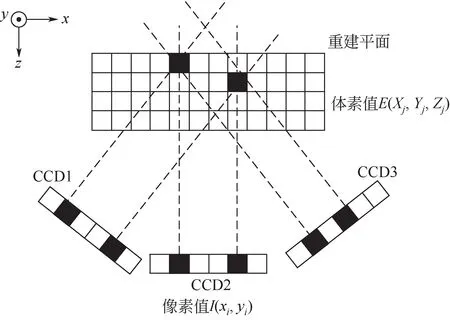
图3 层析重构算法
在得到权重系数后,由于矩阵阶数很大,难以用常规的矩阵方法求解,故通常采用迭代法求解。目前经常采用的算法为ART 算法和MART 算法,这两种算法均通过选择一个合适的初始值E(X,Y,Z)0开始进行E(X,Y,Z)的迭代,且由于其采用了不同的迭代方式,导致了两种算法的收敛速度不同,同时求解精度也有一定程度上的差异。
本文采用了基于乘法视距的MLOS 算法[21],该算法与MART 算法类似,但不需要得到加权矩阵,而是通过视距估计,确定了粒子在整个体积中可能存在的位置,能够极大减少运算量,提高程序运行速度,并在一定程度上降低重建噪声。
MLOS算法是通过每个体素和像素强度的映射关系找出体素空间中的非零体素的方法,针对空间的任一体素,可以通过每台相机的视线找到其在各个相机上的投影;若要使该点的体素强度大于0,则对应位置的像素强度也一定大于0。同样地,像素强度的乘积也一定大于0,这就使得可以通过相应像素的乘积来判断是否存在可以忽略的体素。如图3所示,当相应像素沿视线相乘时,只有每幅图像中非零像素相交的视线所对应的体素为非零体素。该算法通过对每台相机的标定结果的分析就能够直接找到对应像素点,而不需要对体积中的每个点进行极为耗时的权重矩阵计算和储存。
但MLOS 算法与MART 算法一样,均无法去除伪影粒子的存在。伪影粒子是由于该点体素强度能够满足在不同方向投影而产生的,这就意味着重建图像虽然在数学上与原始图像相同,但实际上该点并不存在相应粒子。但在经过多次迭代修正后,伪影粒子的强度通常低于真实粒子。故虽然存在伪影粒子,但其对后续的三维互相关计算的影响很小。
2 实验平台与系统
2.1 实验管段
针对某矩形截面的水流直管段,管道截面尺寸60mm×60mm,管长1500mm,通过某35W水泵提供动力,并在管道前端安装两个稳流器稳定水流,管道中部安装直径5mm的圆柱体作为扰流装置,将整个管道分为两个层流段、一个绕流段和一个尾流段。本实验主要在图4中虚线框所示的测量区域尾流段中进行。图5为本实验的实验装置的结构示意。
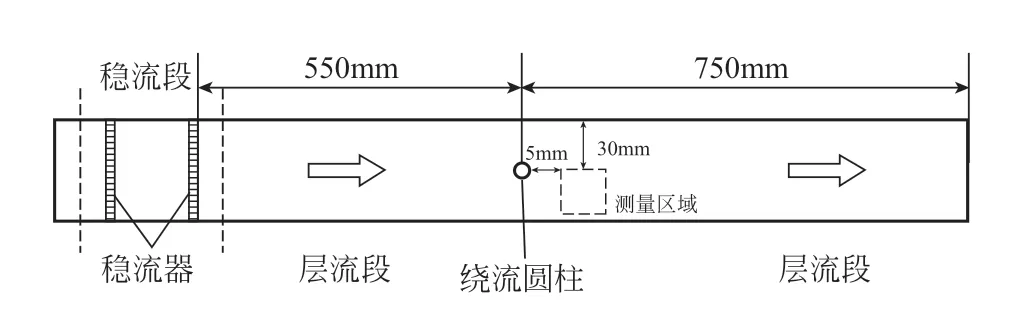
图4 槽道流实验平台管道结构
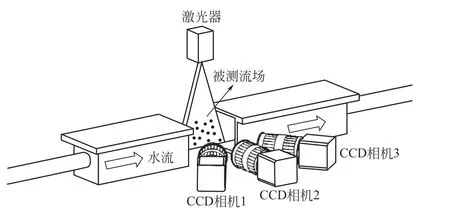
图5 三目层析PIV测量装置
2.2 实验设备
本实验采用了3 台带有PIV 功能的IMPERX 相机,型号为B1411,其中一台为彩色相机,两台为黑白相机,相机分辨率像素均为1360×1364;镜头采用创威工业镜头,型号为CW-VM0418-3MP-1/1.8,焦距范围4~18mm,通光口径为F1.6,可以通过调节光圈对景深进行控制。
通常PIV实验均采用Nd:YAG双脉冲式激光器作为照明光源,因其有脉冲能量高、脉冲间隔短的优点,适用于高速流动下极小颗粒的拍摄;但该类激光器价格昂贵且调试过程复杂,且本实验拍摄对象为低速流体,对脉冲间隔要求不高,故定制了波长450nm、功率4W 的连续激光器,经测试其光强完全可以满足本实验需求,但若使用连续照明会导致PIV模式下第二帧图像过曝,故采用了信号发生器控制激光器,实现脉宽1ms的脉冲式照明。
通常示踪粒子的基本要求为跟随性好、可见度高,使得图像有尽可能高的信噪比。本实验的实验条件为水,故选择了15μm的聚苯乙烯颗粒。
2.3 实验参数设置
实验前通过流量计测得管道水流平均速度为400L/h,可得流速约为0.04m/s,相机放大倍率约为0.1,PIV实验中一般粒子运动距离为5~10个像素,同时曝光时间内粒子运动距离为1~3个像素,故设置两帧间隔为5ms,曝光时间1ms。
3 结果与分析
3.1 三维标定结果
三台相机的标定结果如图6所示,由上至下分别对应为左、中、右三台相机的标定结果,从左到右表示世界坐标系下被离散成体素的空间区域后在像素坐标系下x、y、z三个方向的投影。由于本实验中相机是在同一高度上成一定角度布置,并使标定板平面与中间一台相机的成像平面平行,左右两台相机对称放置于z轴两侧,与中间相机夹角30°,且严格遵循沙姆定律[22],因此中间相机的三个方向投影应大致一致,两侧两台相机的zworld轴投影结果应具有左右对称性,可以看出标定结果与预期基本相符。
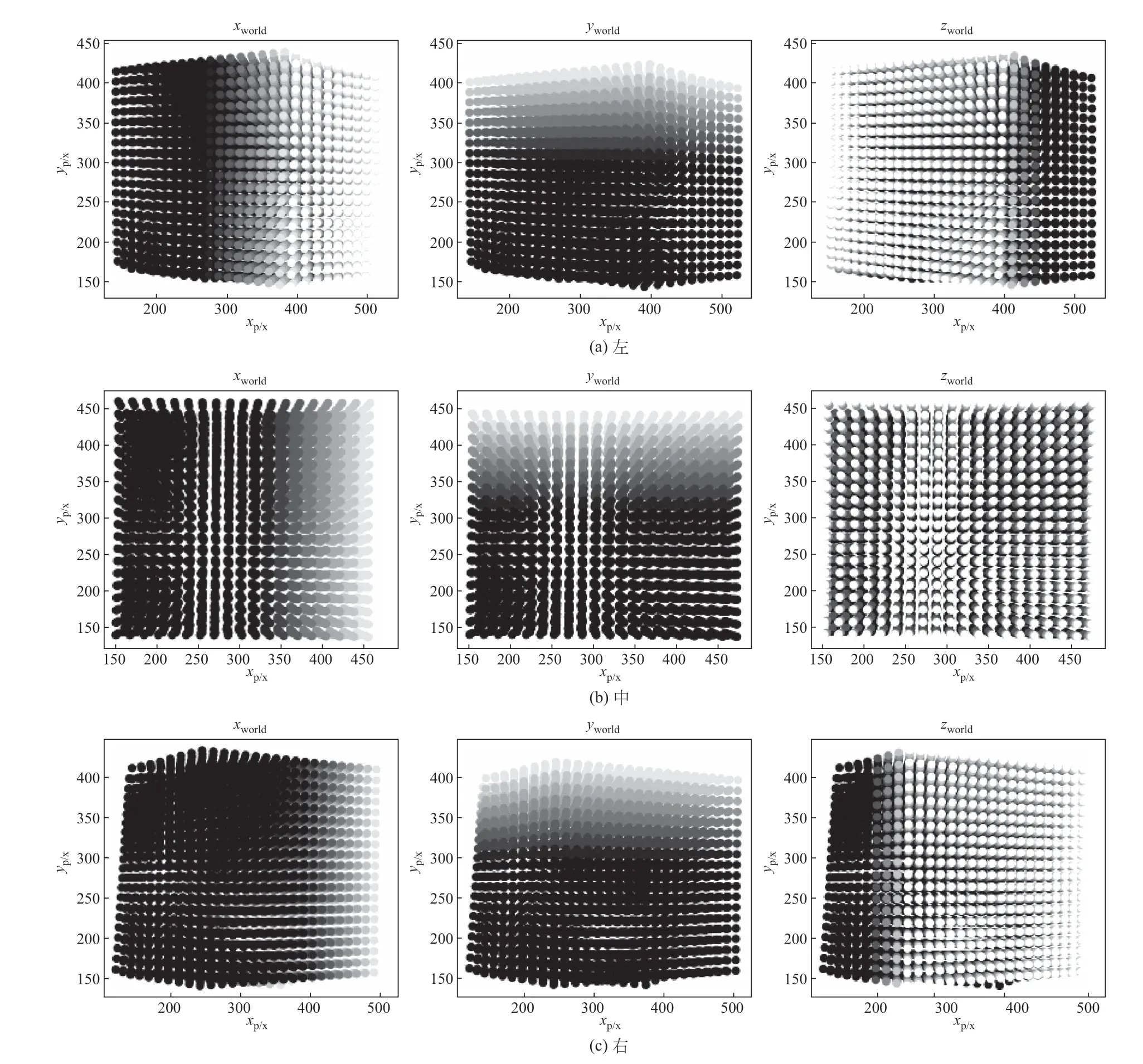
图6 左、中、右三台相机的标定结果
3.2 三维重建结果及分析
3.2.1 重建结果
实验拍摄区域为圆柱后方约5mm 位置,重建区域被离散成600×600×100个体素,重构区域实际大小为30mm×30mm×5mm,空间分辨率约为20voxels/mm,矢量密度为1.6points/mm;由于粒子运动距离约为10个像素,每个体素含1个像素,故选择163voxels为查询窗口,重叠步长为50%,每台相机图像重建平均时间约为9.59s。图7 为某时刻下重建的粒子场z方向不同位置的两张切片图,图片中的明显亮点即为重建得到的粒子,其中部分采用红圈圈出作为示意。
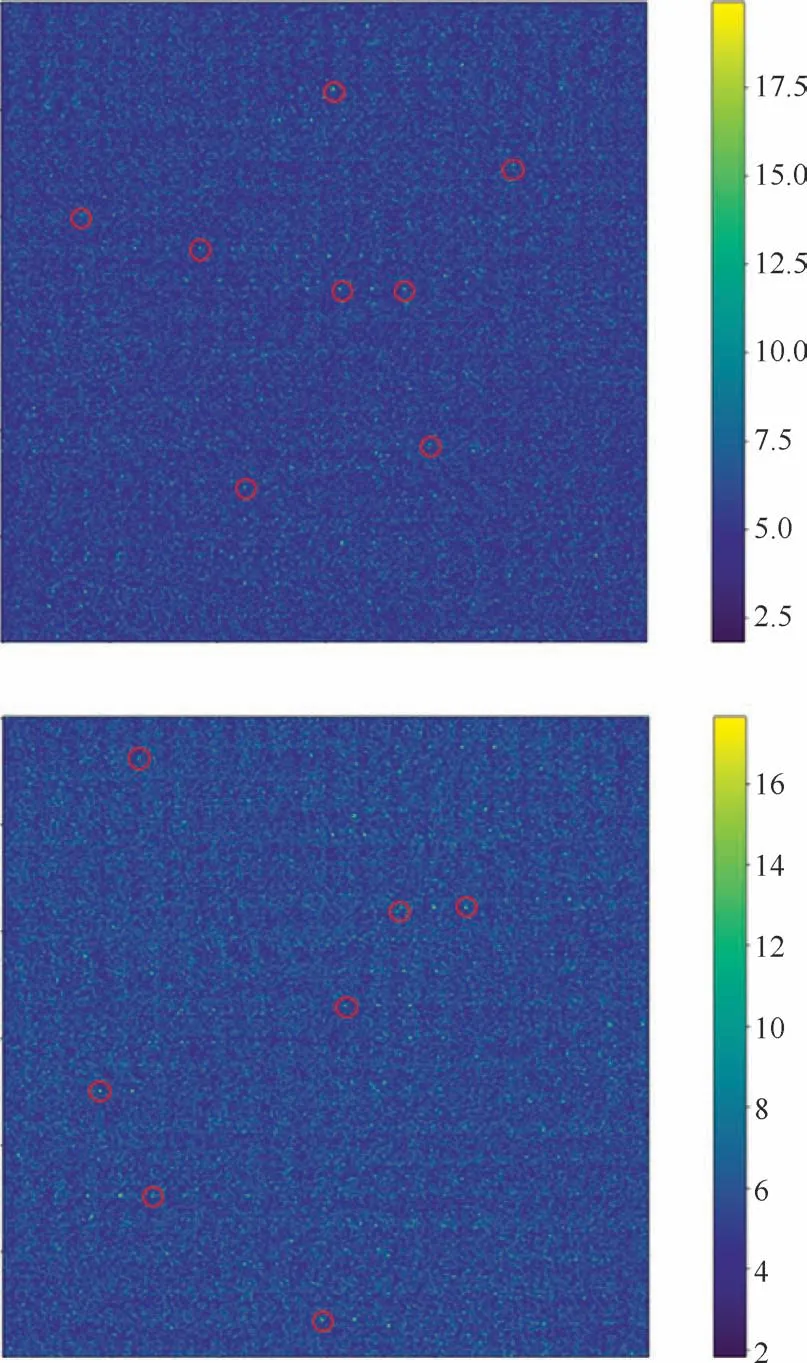
图7 三维粒子场重建切片图
3.2.2 重投影误差分析
由于实际实验中无法得到真实粒子场的切片,因此需要引入重投影误差对重建精度进行分析,即通过重建后的粒子场投影与初始粒子场图片进行比较,重投影误差的计算如式(7)所示。
式中,Er为重投影误差;(u,v)为图像的像素坐标;I0代表已知的初始粒子场图片;I代表重建后投影得到的粒子场图片,由重建后的粒子场通过式(1)计算得到。
随机选取中间视角相机两个不同时刻的三维重建结果,图8为相应的重投影相对误差分布,平均重投影相对误差不超过0.5%,具有相对较高的重建精度。
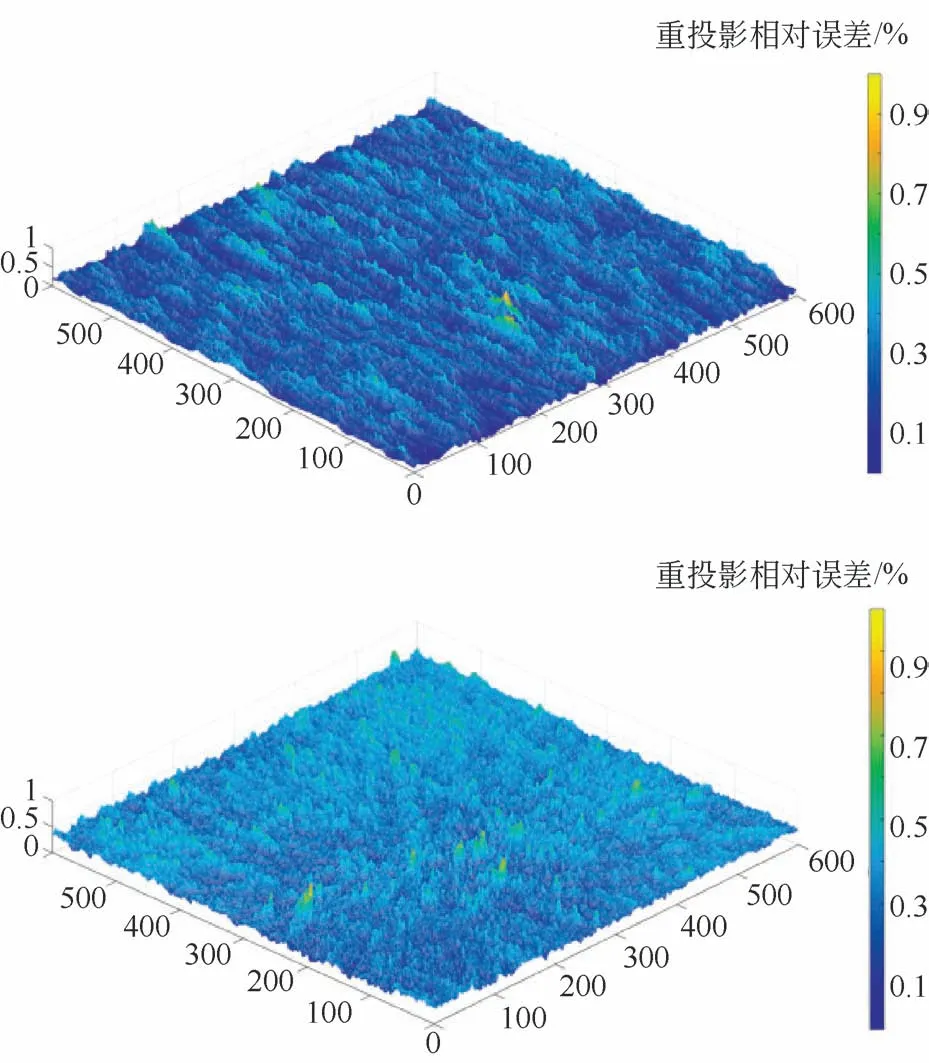
图8 典型的重投影相对误差分布
3.3 互相关计算结果
计算结果如图9、图10 所示,分别展示了圆柱后方某法向-流向切平面的涡量图和流场图。所测量位置为圆柱后方约5mm 位置处的下半部分区域,区域位置如图4 虚线框所示,包含了圆柱绕流形成的卡门涡街以及下方层流部分。图9 中可看到不同时刻旋涡的演化状态,交替出现的红色与蓝色区域显示了圆柱尾流上下方形成的具有一定规则的、交叉排列的涡列,并沿下游方向有扩散的趋势,这雨流体力学中圆柱尾迹卡门涡街的理论相一致。其中蓝色涡量为顺时针方向旋转的负涡量。
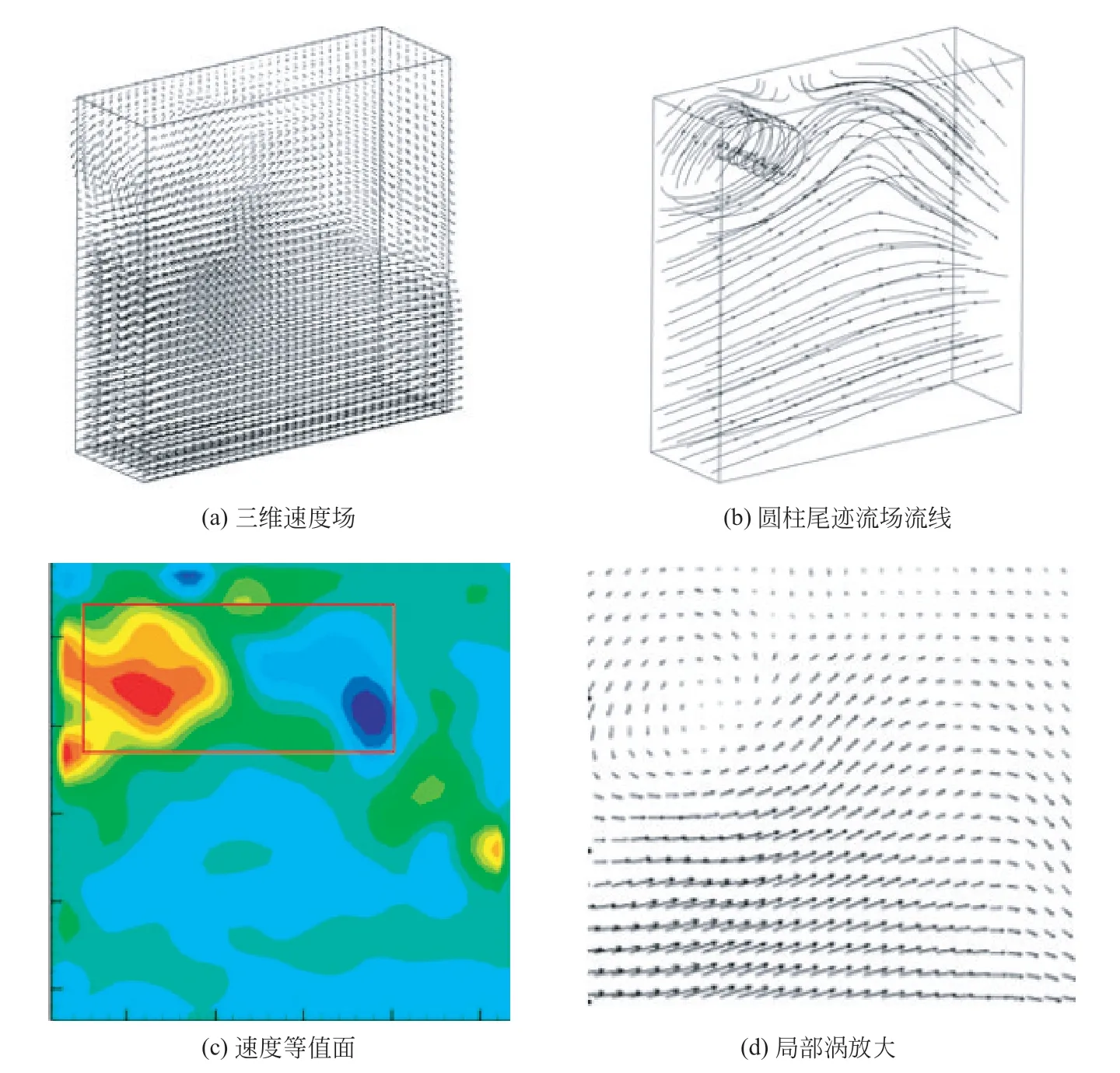
图10 互相关计算结果
三维速度场的重建结果如图10(a)所示,整个重建空间内包含72×72×9个矢量,所含矢量信息较多,故同时显示相应流线图[图10(b)]和某截面涡量图[图10(c)]。可以看出流场左上方形成了一个明显的涡环结构,同时其右侧存在一旋转方向相反、交替排列的涡,同时具有向下游方向扩散的趋势,与理论结果基本相符。图10(d)为图10(c)中红框位置处形成涡环的局部放大图。
4 结论与展望
(1)本文基于三目视觉搭建了一套层析PIV测量系统,针对矩形水流管道中的圆柱尾迹流动进行了采集实验,进行了三维标定以及重建,最终的测量结果显示,该层析PIV测量系统得到的三维速度场能够合理地反映圆柱尾迹出口处的流动结构,成功观测到了卡门涡街结构。
(2)本实验的实际测量区域为30mm×30mm×5mm,故体素大小设置为600×600×100,空间分辨率达到20voxels/mm,互相关计算结果包含72×72×9 个矢量信息,相比于常规PIV 获得了更加丰富的三维流场信息。
(3)MLOS 算法能够有效降低重构所耗时间,每台相机的平均重建时间约为9.59s;同时能够保持较高的重建精度,重投影误差不超过0.5%;虽然MLOS算法无法消除伪影粒子的存在,但通过数次迭代计算大大降低了伪影粒子对最终互相关计算的影响。
(4)通过在低速条件下对复杂流场结构的测量,验证了本文采用的三目层析PIV系统及布置方式的可行性为后续狭小空间区域流场测量研究奠定了基础。

