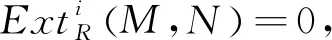强X-Gorenstein投射模

王 琦

(兰州职业技术学院 初等教育学院， 甘肃 兰州 730070)

1.预备知识

本节中我们给出全文所需的一些概念和记号，分别用P、F表示投射R-模和平坦R-模构成的类.

定义1.1称R-模M是Gorenstein投射的,如果存在一个R-模的正合序列

…→P1→P0→P0→P1→…,

使得以下三条成立:

(1)M≅Im(P0→P0);

(2)所有的Pi和所有的Pi都是投射的;

(3)对任意的投射模Q，函子HomR(-,Q)仍保持该序列的正合性.

记所有 Gorenstein 投射R-模构成的模类为GP(R).(见文献[1])

定义1.2称模M是Ding投射的,如果存在一个模的正合序列

…→P1→P0→P0→P1→…,

使得以下三条成立:

(1)M≅Im(P0→P0);

(2)所有的Pi和所有的Pi都是投射的;

(3)对任意的平坦模F,函子HomR(-,F)仍保持该序列的正合性.

记所有 Gorenstein 投射R-模构成的模类为DP.(见文献[4])

定义1.3设X是一个具有投射可解性的模类。 称模M是X-Gorenstein投射的,如果存在一个模的正合序列

…→P1→P0→P0→P1→…,

使得以下三条成立:

(2)所有的Pi和所有的Pi都是投射的;

(3)对任意的X∈X，,函子HomR(-,X)仍保持该序列的正合性。

记所有X-Gorenstein投射R-模构成的模类为XGP(R).(见文献[8])

定义1.4称模M是强Gorenstein投射的，如果存在一个如下形式的HomR(-,P(R))正合的正合序列

使得M=Kerf,且P是投射的, 记所有强Gorenstein投射模构成的模类为SGP(R).显然P(R)⊆SGP(R),且SGP(R)⊆GP(R).(见文献[3])

定义1.5称模M是强“Ding”投射的，如果存在一个如下形式的HomR(-,F(R))正合的正合序列

使得M=Kerf,且P是投射的, 记所有强“Ding”投射模构成的模类为SDP.

结构域(L613-P1193)，且距离催化中心位置(H959-H963)[3]非常近，推测L983P可能通过空间构象的改变影响ACE蛋白的催化功能，但以上两个变异位点如何真正影响蛋白功能仍需要进一步的功能验证和分析。

其它未说明的记号可参考文献[1]、[4]、[7]、[9].

2.主要结论

定义2.1设模类X是投射可解的,称模M是强X-Gorenstein投射的,如果存在一个如下形式的正合序列

使得:

(1)P是投射的;

(2)M=Kerf;

(3)对任意的X∈X,HomR(-,X)保持该序列的正合性.

记所有强X-Gorenstein投射模构成的模类为SXGP.

注记2.2设X是一个投射可解性的模类，显然

(1) SXGP(R)⊆XGP(R);

(2) SXGP(R)对任意直和封闭;

(3)当X=P(R)时, SXGP(R)即SGP(R),当X=F(R)时, SXGP(R)即SDP(R);

(4) SXGP(R)⊆SGP(R).

定理3一个模是X-Gorenstein投射的当且仅当它是某个强X-Gorenstein投射模的直和因子.

证明:(⟸)由文献[8]中定理2.3及注记2.2可证.

(⟹)设M是X-Gorenstein投射模,则存在一个HomR(-,X)正合的投射模构成的正合序列

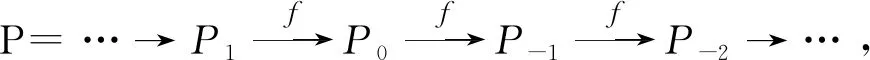
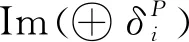
使得M=Im(f).

对于所有的m∈,用P[m]表示由P平移m各单位得到的正合序列:

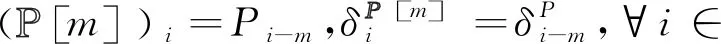
考虑正合序列

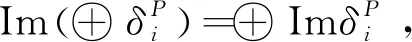
引理2.4设M是一个模,则以下条件等价:

(1)M是强X-Gorenstein投射的;

(2)存在一个HomR(-,X)-正合的短正合序列0→M→P→M→0,其中P是投射模.

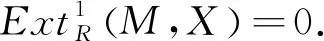
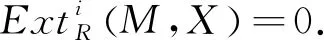
证明:类似文献[5]命题2.4的证明.

推论2.5每个投射模是强X-Gorenstein投射的.

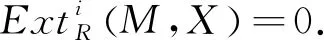
定理2.6以下条件等价:

R是半单环;

(2)所有左R-模是强DP-Gorenstein投射的;

(3)所有右R-模是强DP-Gorenstein投射的.